2026年中考数学复习课件 专题五 函数与几何(共64张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题五 函数与几何(共64张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 07:48:59 | ||
图片预览










文档简介
(共64张PPT)
复习讲义
第二篇 专题突破
专题五 函数与几何
函数与几何综合题主要有两类:一类是以几何图形为背景,根据
其中的几何元素(线段、周长、面积等)的数量关系建立函数模型;
另一类是以函数为背景,用函数的图象与性质来探究几何图形中几何
元素之间的关系.
类型一 以几何知识为背景的函数问题
从题目形式看,以几何知识为背景的函数问题一般是先给定几何
图形,再结合几何图形的性质,得到相应几何元素之间的数量关系,
由此建立函数模型,结合函数的性质探究几何图形.在运用函数的性质
解决几何图形中的问题时,要结合图形确定自变量的取值范围.这类题
目考查的方向一般有:求几何元素之间满足的函数解析式或函数图
象,求几何图形中点的坐标;用函数的性质描述几何元素之间的关
系,根据函数图象求线段长,等等.
典题精析
图1
例1 (2025·六安·中考模拟)如图1, 是边长为4的等边三
角形,点,,分别在边,, 上运动,且满足
.
(1)求证: .
证明:是等边三角形,, .
又, ,即.
在和 中,,,, .
思路点拨(1)由等边三角形的性质,可得 ,又已知,则只需证明,即可用“ ” 证明 .
(2)设的长为,的面积为,求关于 的函数解析式.
图1
思路点拨 (2)求关于的函数解析式就是用含 的代数式表示的面积.直接求 的面积难度较大,可以考虑运用面积的和差法计算, .注意,要结合图形特征写出自变量 的取值范围.
图1
图113
解:如图113,分别过点,作, ,垂足分别为, .
在等边三角形中, ,
, ,
.
的长为, ,
.
.
同理可证
的面积为,∴ .
图113
(3)结合(2)所得的函数,描述的面积随 的增大如何变化.
图1
解:由(2)知,.
,这个函数图象的对称轴为直线, 当时,随 的增大而减小;当时,随 的增大而增大.
即当0时,的面积随 的增大而减小;当2时,的面积随 的增大而增大.
思维点拨:(3)由(2)可得y关于x 的函数所析式,根据此函数的性质描述△DEF的面积随AD的增大的变化情况即可.
针对训练
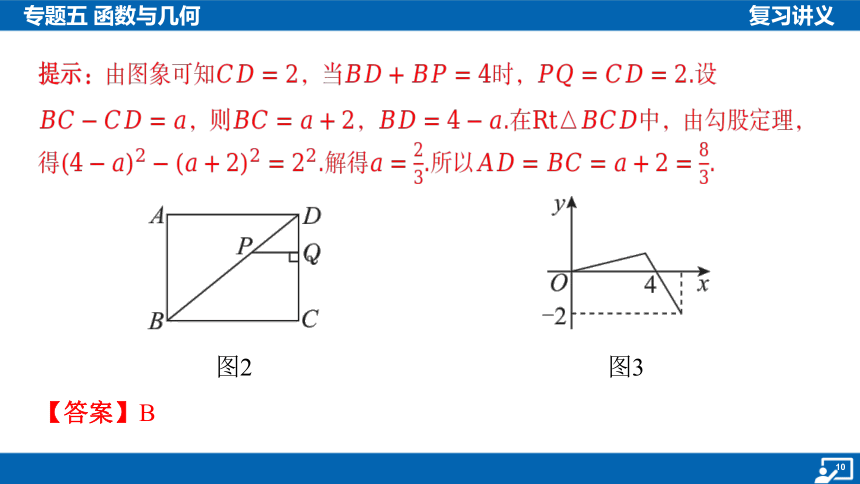
1.(2024·甘肃临夏·中考)如图2,在矩形中, 为其对角线,一
动点从点出发,沿着的路径行进,过点作 ,垂
足为.设点的运动路程为,为,与 的函数图象如图3,
则 的长为( ).
图2
图3
A. B. C. D.
提示:由图象可知,当时, .设
,则,.在 中,由勾股定理,
得.解得.所以 .
图2
图3
【答案】B
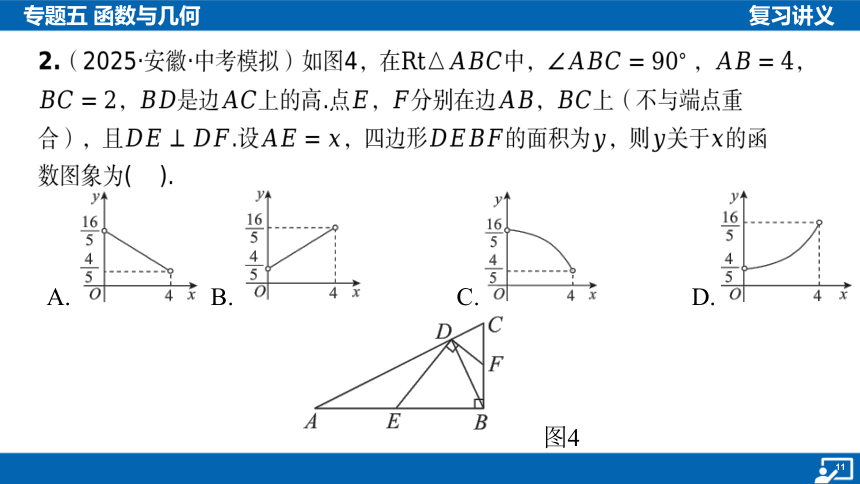
2.(2025·安徽·中考模拟)如图4,在中, , ,
,是边上的高.点,分别在边, 上(不与端点重
合),且.设,四边形的面积为,则关于 的函
数图象为( ).
图4
A. B. C. D.
图4
提示:过点D作于点.在 中,
由勾股定理,得 .从而得
.在 中,由勾股定理,
得 .由此可得
.所以 .因此
,
.因为
,
,所以
.由此可得, .
故 .所以
.
又,所以随的增大而减小,且与 的
函数图象为线段(不含端点).
【答案】A
图4
3.(2024·天津·中考)如图5,将一个平行四边形纸片 放置在平面
直角坐标系中,已知点,点,点, 在第一象限,且
, .
图5
图5
(1)填空:如图5,点 的坐标为 _______,点
的坐标为_______.
提示:过点作于点.在
中, ,
. 四边形
是平行四边形, , 点到 轴的距离为
,点到轴的距离为,即点的坐标为 .
图6
(2)如图6,若为轴的正半轴上一动点,过点
作直线轴,沿直线折叠该纸片,折叠后点
的对应点落在轴的正半轴上,点的对应点为 .
设 .
①如图6,直线与边相交于点 ,当折叠后四边
形与重叠部分为五边形时, 与
相交于点.试用含有的式子表示线段 的长,
并直接写出 的取值范围.
解:由折叠的性质,得 ,
,
四边形 为平行四边形, ,
, .
是等边三角形.
, .
当点与点重合时,与的交点 与点重合,.
当点与点重合时,与的交点 与点重合,. 的取值范围为 .
图6
②设折叠后重叠部分的面积为,当时,求 的取值范围(直接写出结果即可).
图6
图114
提示:如图114,直线与边相交于点 ,连接,过点作于点 ,此时 , ,即. ,当时,随着的增大而增大. .
图115
如图115,直线与边相交于点.当 时.
, 随着的增大而增大. 当 时, . 如图116,当时,直线与边 相交于点,与相交于点,过点作 轴.
图116
图116
由①可知是等边三角形,∴ . . . , 当时, 有最大值,最大值为.
又, 当 时, .
图117
如图117,当时,直线与边 相交与点
.
【答案】的取值范围为 .
, 随着的增大而减小.
当时, .综上所述,
.
类型二 以函数知识为背景的几何问题
从题目的形式看,以函数知识为背景的几何问题一般是先给定函
数图象或函数解析式,然后根据已知函数图象中几何图形的位置特
征,用函数解析式表示点的坐标(或线段的长),结合函数、几何图
象的性质运用数形结合方法解决有关函数与几何的问题.这类题目考查
的方向一般有:求函数的解析式、点的坐标;求图象上的点满足什么
条件时,几何图形是等腰三角形、直角三角形、平行四边形、矩形、
菱形、正方形等;已知两个三角形全等或相似,求点的坐标;探索线
段、面积等的最值问题;已知周长或面积之间满足一定关系时,求点
的坐标;等等.
典题精析
图7
例2 (2025·广西梧州·模拟)如图7,二次函数
的图象交轴于点, ,交
轴于点,点是直线 上方的二次函数图
象上的一个动点,过点作轴,垂足为点 ,
交于点 .
图7
(1)求这个二次函数的解析式和点 的坐标.
解:将,代入 ,得解得
.
令,即,解得 ,
点的坐标为 .
思路点拨(1)将, 代入可求得,的值,令 可求得点 的坐标.
(2)连接,交轴于点 .
图7
①当时,求点 的坐标.
思路点拨 (2)①观察图象,可发现 ,,且 ,由此可得相似三角形,从而得到相关线段的比例式.设点 的横坐标为,点在抛物线上,点是直线与线段 的交点,则可根据抛物线和直线对应的函数解析式,用含 的代数式表示出这两点的纵坐标,再表示出相关线段的长,根据列出关于 的方程,求解即可.
图7
解:由点在抛物线上,可设点 的坐标为,
,
,即 .
.
设直线 对应的函数解析式为.
将,代入,得解得
直线对应的函数解析式为
.
当 时,,解得, (舍去).
则, 点的坐标为 .
图7
②连接,四边形有可能是正方形吗 如果有可能,那么此时
的正切值是多少 如果没有可能,那么请说明理由.
解:四边形有可能是正方形.
同①设点 的坐标为,则
思维点拨:②先设法证明四边形 是平行四边形,由 ,可得四边形 是矩形.则当时,矩形是正方形.由此建立关于 的方程,可求出四边形是正方形时 的值. 再求出,的长即可得 的正切值.
图7
图7
, 四边形是平行四边形.
, 四边形是矩形.
当时,矩形是正方形.
则 ,解得.
,.∵ , .
.
针对训练
图8
4.(2025·武汉·中考模拟)如图8,过 的图象
上的点,分别作轴、轴的平行线交 的图象于
点,.以,为邻边的矩形 被坐标轴分割成
四个小矩形,面积分别记为,,, .若
,则 的值为( ).
A.4 B.3 C.2 D.1
图8
提示:设.在中,令,得 ;
令,得.所以, .所
以.所以,, .因为
,所以.解得 .经检
验, 是分式方程的解,且符合题意.
【答案】C
5.(2024·新疆·中考)如图9,抛物线与轴交于点 ,
与轴交于点,线段在抛物线的对称轴上移动(点在点 下方),
且.当的值最小时,点 的坐标为______.
图9
图118
提示:如图118,作点关于抛物线对称轴的对称点 ,
点向下平移3个单位长度,得到点,连接 ,交
对称轴于点,此时 的值最小,
.在中,令 ,则
.从而得.令,则 ,解
得,.从而得.抛物线 的对称轴为直
线,由此可得,.设直线 对应的函数解析式为
,将,代入,得
解得所以直线 对应的函数解析式为
.当时,,所以点 的坐标为
.
【答案】
图118
6.(2024·黑龙江牡丹江·中考)如图10,在平面直角坐标系中,直线
与轴的正半轴交于点,与轴的负半轴交于点,点在 轴
的正半轴上,四边形是平行四边形,线段 的长是一元二次方程
的一个根.请解答下列问题.
图10
备用图
(1)求点 的坐标.
图10
解:解方程,得,
,即点 的坐标为.
把代入,得
.令 ,得
点的坐标为 .
(2)如图10,线段的垂直平分线交直线于点,交轴于点 ,交于点,点在第一象限,,连接,求 的值.
图10
图119
解:如图119,过点作于点
,,
,.
∴
图119
∵ 四边形是平行四边形, ,
,
是的垂直平分线, ,,即.
在和 中,,,,
, .
.
.
又,
∴
.
图119
(3)在(2)的条件下,点在直线上,在轴上是否存在点 ,使以
,,为顶点的三角形是直角边比为 的直角三角形?若存在,则直
接写出的个数和其中两个点 的坐标;若不存在,则说明理由.
图10
备用图
提示:如图120,当 时,符合题意的 有4个,
.如图121,当 时,符合题意的 有4个,
,,,.如图122,当 时,
符合题意的有4个,,,,
图120
图121
图122
【答案】存在,符合题意的的个数为12,点的坐标为 或
或或或 (写出两个即可).
专题练习五 函数与几何
类型一 以几何知识为背景的函数问题
图1
1.(2024·黑龙江齐齐哈尔·中考)如图1,
在等腰直角三角形 中,
, ,动点, 同
时从点出发,分别沿射线和射线 的方向匀速运动,且速度大小相同,当点停止运动时,点 也随之停止运动,连接,以为边向下画正方形. 设点 运动的路程为,正方形和等腰直角三角形 重合部分的面积为.下列图象能反映与 之间函数关系的是( ).
B.
C D.
图1
图1
提示:当正方形与等腰直角三角形 的重合部分全部在 内部时,重合部分的面积即为正方形的面积,此时正
【答案】A
方形的边长随着 的增大而增大,对应的函数解析式为
,这一部分是开口向上的抛物线,只有选项A,B符合. 当重合部分是正方形 的一部分时,重合部分是一个矩形,且随着 的增大,这个矩形的长在增大,宽在减小,对应的函数解析式为 ,这一部分是开口向下的抛物线,故选项A符合.
2.(2024·重庆·中考)如图2,在中,,,为 上
一点,,过点作交于点.点,的距离为 ,
的周长与的周长之比为 .
图2
(1)请直接写出,分别关于的函数解析式,并写出自变量 的取值范围.
提示: , ,. ,. , 为上一点, .
图2
答案:,.
(2)在图3的平面直角坐标系中,画出函数, 的图象,并分别写出
函数, 的一条性质.
图3
解:函数,的图象如图138所示.
的图象性质:当时,随 的增大而增大.
的图象性质:当时,随 的增大而减小.
图138
(3)结合函数图象,请直接写出时 的取值范围(近似值保留小数点后一位,误差不超过 ).
图3
解:当时,的取值范围为 .
3.(2025·广西河池·模拟)如图4,已知是边长为 的等边三角形,动点,同时从,两点出发,分别沿, 匀速运动,其中点运动的速度是,点运动的速度是,当点到达点 时,,两点都停止运动.设运动时间为 ,解答下列问题:
图4
(1)设的面积为,求与 的函数解析式.
解:如图139,过点作于点.
由题意,得,.
是等边三角形, , .
,
,即 .
图139
(2)作交于点,连接,当为何值时, .
图4
解: , , .
是等边三角形.
.
,
.
图4
又 , 四边形是平行四边形.
.
又 , 四边形是矩形.
.
当时, ,又
, .
解得.
当 时, .
类型二 以函数知识为将背景的几何问题
图5
4.如图5,已知直线与轴、 轴分别交于
,两点,是以 为圆心,1为半径的圆上
一动点,连接,.则 面积的最大值是
( ).
A. B.
C.10.5 D.11.5
图140
提示:将代入,得 .故点B
的坐标为.令,则 ,解得
.故点A的坐标为.由此可得, ,
.在 中,由勾股定理,得
.如图140,过点C作 于点,连接 .
由三角形面积公式,得 ,即
.解得.上的点到直线 的最大
距离是.故面积的最大值是 .
【答案】C
5.(2024·江苏苏州·中考)如图6,中, ,, ,,反比例函数 的图象与交于点,与交于点 .
图6
(1)求, 的值.
解: ,,
,
, ,.
设直线 对应的函数解析式为,将, 代入,得
图6
解得
∴直线 对应的函数解析式为.
将点代入,得. 解得
.
将代入,得.解得 .
图6
(2)为反比例函数 图象上
一动点(点在点,之间运动,不与, 两点
重合),过点作,交轴于点,过点
作轴,交于点,连接,求
面积的最大值,并求出此时点 的坐标.
解:如图141,延长交轴于点,交于点 .
, , .
轴, , .
, .
图141
,即
.
设点的坐标为,, ,则,,
.
当 时,有最大值,为,此时点的坐标为, .
图141
6.(2025·广西贵港·模拟)在平面直角坐标系中,抛物线
与轴交于点和点(点在点 的左侧),
与轴交于点.若线段,,的长满足 ,则这样的
抛物线称为“黄金”抛物线.如图7,抛物线 为“黄
金”抛物线,其与轴的交点分别为点,点(其中点在点 的右侧),
与轴交于点,且 .
图7
备用图
(1)求抛物线 对应的函数解析式.
解:将代入,得
为“黄金”抛物线, .
又 ,
,
点在点 的右侧, ,.
将,代入 ,得
解得
该抛物线对应的函数解析式为 .
图7
(2)为上方抛物线上的动点,过点作 ,垂足为 .
图7
①求 的最大值.
图142
解:如图142,过点作轴于点,交 于点,则 ,
.
由(1)知,,∴ .
.
,即.
要使最大,只要 最大即可.
设直线对应的函数解析式为 ,将
,代入,得 解得
直线对应的函数解析式为 .
设,,则,,
为上方抛物线上的动点,∴
当时,有最大值,为
∴ 的最大值为 .
图142
②连接,当与相似时,求点 的坐标.
图143
解:当时,, 轴.
点与点的纵坐标相等,为2.将 代入,得 .
解得, 点的坐标为 .
当时, .
如图143,过点作轴于点,交于点
轴,
, .
在和 中, , ,,
.
设点的坐标为,,则 , .
,即
, .
则.
点的坐标为, .
综上所述,点的坐标为或, .
图143
复习讲义
第二篇 专题突破
专题五 函数与几何
函数与几何综合题主要有两类:一类是以几何图形为背景,根据
其中的几何元素(线段、周长、面积等)的数量关系建立函数模型;
另一类是以函数为背景,用函数的图象与性质来探究几何图形中几何
元素之间的关系.
类型一 以几何知识为背景的函数问题
从题目形式看,以几何知识为背景的函数问题一般是先给定几何
图形,再结合几何图形的性质,得到相应几何元素之间的数量关系,
由此建立函数模型,结合函数的性质探究几何图形.在运用函数的性质
解决几何图形中的问题时,要结合图形确定自变量的取值范围.这类题
目考查的方向一般有:求几何元素之间满足的函数解析式或函数图
象,求几何图形中点的坐标;用函数的性质描述几何元素之间的关
系,根据函数图象求线段长,等等.
典题精析
图1
例1 (2025·六安·中考模拟)如图1, 是边长为4的等边三
角形,点,,分别在边,, 上运动,且满足
.
(1)求证: .
证明:是等边三角形,, .
又, ,即.
在和 中,,,, .
思路点拨(1)由等边三角形的性质,可得 ,又已知,则只需证明,即可用“ ” 证明 .
(2)设的长为,的面积为,求关于 的函数解析式.
图1
思路点拨 (2)求关于的函数解析式就是用含 的代数式表示的面积.直接求 的面积难度较大,可以考虑运用面积的和差法计算, .注意,要结合图形特征写出自变量 的取值范围.
图1
图113
解:如图113,分别过点,作, ,垂足分别为, .
在等边三角形中, ,
, ,
.
的长为, ,
.
.
同理可证
的面积为,∴ .
图113
(3)结合(2)所得的函数,描述的面积随 的增大如何变化.
图1
解:由(2)知,.
,这个函数图象的对称轴为直线, 当时,随 的增大而减小;当时,随 的增大而增大.
即当0时,的面积随 的增大而减小;当2时,的面积随 的增大而增大.
思维点拨:(3)由(2)可得y关于x 的函数所析式,根据此函数的性质描述△DEF的面积随AD的增大的变化情况即可.
针对训练
1.(2024·甘肃临夏·中考)如图2,在矩形中, 为其对角线,一
动点从点出发,沿着的路径行进,过点作 ,垂
足为.设点的运动路程为,为,与 的函数图象如图3,
则 的长为( ).
图2
图3
A. B. C. D.
提示:由图象可知,当时, .设
,则,.在 中,由勾股定理,
得.解得.所以 .
图2
图3
【答案】B
2.(2025·安徽·中考模拟)如图4,在中, , ,
,是边上的高.点,分别在边, 上(不与端点重
合),且.设,四边形的面积为,则关于 的函
数图象为( ).
图4
A. B. C. D.
图4
提示:过点D作于点.在 中,
由勾股定理,得 .从而得
.在 中,由勾股定理,
得 .由此可得
.所以 .因此
,
.因为
,
,所以
.由此可得, .
故 .所以
.
又,所以随的增大而减小,且与 的
函数图象为线段(不含端点).
【答案】A
图4
3.(2024·天津·中考)如图5,将一个平行四边形纸片 放置在平面
直角坐标系中,已知点,点,点, 在第一象限,且
, .
图5
图5
(1)填空:如图5,点 的坐标为 _______,点
的坐标为_______.
提示:过点作于点.在
中, ,
. 四边形
是平行四边形, , 点到 轴的距离为
,点到轴的距离为,即点的坐标为 .
图6
(2)如图6,若为轴的正半轴上一动点,过点
作直线轴,沿直线折叠该纸片,折叠后点
的对应点落在轴的正半轴上,点的对应点为 .
设 .
①如图6,直线与边相交于点 ,当折叠后四边
形与重叠部分为五边形时, 与
相交于点.试用含有的式子表示线段 的长,
并直接写出 的取值范围.
解:由折叠的性质,得 ,
,
四边形 为平行四边形, ,
, .
是等边三角形.
, .
当点与点重合时,与的交点 与点重合,.
当点与点重合时,与的交点 与点重合,. 的取值范围为 .
图6
②设折叠后重叠部分的面积为,当时,求 的取值范围(直接写出结果即可).
图6
图114
提示:如图114,直线与边相交于点 ,连接,过点作于点 ,此时 , ,即. ,当时,随着的增大而增大. .
图115
如图115,直线与边相交于点.当 时.
, 随着的增大而增大. 当 时, . 如图116,当时,直线与边 相交于点,与相交于点,过点作 轴.
图116
图116
由①可知是等边三角形,∴ . . . , 当时, 有最大值,最大值为.
又, 当 时, .
图117
如图117,当时,直线与边 相交与点
.
【答案】的取值范围为 .
, 随着的增大而减小.
当时, .综上所述,
.
类型二 以函数知识为背景的几何问题
从题目的形式看,以函数知识为背景的几何问题一般是先给定函
数图象或函数解析式,然后根据已知函数图象中几何图形的位置特
征,用函数解析式表示点的坐标(或线段的长),结合函数、几何图
象的性质运用数形结合方法解决有关函数与几何的问题.这类题目考查
的方向一般有:求函数的解析式、点的坐标;求图象上的点满足什么
条件时,几何图形是等腰三角形、直角三角形、平行四边形、矩形、
菱形、正方形等;已知两个三角形全等或相似,求点的坐标;探索线
段、面积等的最值问题;已知周长或面积之间满足一定关系时,求点
的坐标;等等.
典题精析
图7
例2 (2025·广西梧州·模拟)如图7,二次函数
的图象交轴于点, ,交
轴于点,点是直线 上方的二次函数图
象上的一个动点,过点作轴,垂足为点 ,
交于点 .
图7
(1)求这个二次函数的解析式和点 的坐标.
解:将,代入 ,得解得
.
令,即,解得 ,
点的坐标为 .
思路点拨(1)将, 代入可求得,的值,令 可求得点 的坐标.
(2)连接,交轴于点 .
图7
①当时,求点 的坐标.
思路点拨 (2)①观察图象,可发现 ,,且 ,由此可得相似三角形,从而得到相关线段的比例式.设点 的横坐标为,点在抛物线上,点是直线与线段 的交点,则可根据抛物线和直线对应的函数解析式,用含 的代数式表示出这两点的纵坐标,再表示出相关线段的长,根据列出关于 的方程,求解即可.
图7
解:由点在抛物线上,可设点 的坐标为,
,
,即 .
.
设直线 对应的函数解析式为.
将,代入,得解得
直线对应的函数解析式为
.
当 时,,解得, (舍去).
则, 点的坐标为 .
图7
②连接,四边形有可能是正方形吗 如果有可能,那么此时
的正切值是多少 如果没有可能,那么请说明理由.
解:四边形有可能是正方形.
同①设点 的坐标为,则
思维点拨:②先设法证明四边形 是平行四边形,由 ,可得四边形 是矩形.则当时,矩形是正方形.由此建立关于 的方程,可求出四边形是正方形时 的值. 再求出,的长即可得 的正切值.
图7
图7
, 四边形是平行四边形.
, 四边形是矩形.
当时,矩形是正方形.
则 ,解得.
,.∵ , .
.
针对训练
图8
4.(2025·武汉·中考模拟)如图8,过 的图象
上的点,分别作轴、轴的平行线交 的图象于
点,.以,为邻边的矩形 被坐标轴分割成
四个小矩形,面积分别记为,,, .若
,则 的值为( ).
A.4 B.3 C.2 D.1
图8
提示:设.在中,令,得 ;
令,得.所以, .所
以.所以,, .因为
,所以.解得 .经检
验, 是分式方程的解,且符合题意.
【答案】C
5.(2024·新疆·中考)如图9,抛物线与轴交于点 ,
与轴交于点,线段在抛物线的对称轴上移动(点在点 下方),
且.当的值最小时,点 的坐标为______.
图9
图118
提示:如图118,作点关于抛物线对称轴的对称点 ,
点向下平移3个单位长度,得到点,连接 ,交
对称轴于点,此时 的值最小,
.在中,令 ,则
.从而得.令,则 ,解
得,.从而得.抛物线 的对称轴为直
线,由此可得,.设直线 对应的函数解析式为
,将,代入,得
解得所以直线 对应的函数解析式为
.当时,,所以点 的坐标为
.
【答案】
图118
6.(2024·黑龙江牡丹江·中考)如图10,在平面直角坐标系中,直线
与轴的正半轴交于点,与轴的负半轴交于点,点在 轴
的正半轴上,四边形是平行四边形,线段 的长是一元二次方程
的一个根.请解答下列问题.
图10
备用图
(1)求点 的坐标.
图10
解:解方程,得,
,即点 的坐标为.
把代入,得
.令 ,得
点的坐标为 .
(2)如图10,线段的垂直平分线交直线于点,交轴于点 ,交于点,点在第一象限,,连接,求 的值.
图10
图119
解:如图119,过点作于点
,,
,.
∴
图119
∵ 四边形是平行四边形, ,
,
是的垂直平分线, ,,即.
在和 中,,,,
, .
.
.
又,
∴
.
图119
(3)在(2)的条件下,点在直线上,在轴上是否存在点 ,使以
,,为顶点的三角形是直角边比为 的直角三角形?若存在,则直
接写出的个数和其中两个点 的坐标;若不存在,则说明理由.
图10
备用图
提示:如图120,当 时,符合题意的 有4个,
.如图121,当 时,符合题意的 有4个,
,,,.如图122,当 时,
符合题意的有4个,,,,
图120
图121
图122
【答案】存在,符合题意的的个数为12,点的坐标为 或
或或或 (写出两个即可).
专题练习五 函数与几何
类型一 以几何知识为背景的函数问题
图1
1.(2024·黑龙江齐齐哈尔·中考)如图1,
在等腰直角三角形 中,
, ,动点, 同
时从点出发,分别沿射线和射线 的方向匀速运动,且速度大小相同,当点停止运动时,点 也随之停止运动,连接,以为边向下画正方形. 设点 运动的路程为,正方形和等腰直角三角形 重合部分的面积为.下列图象能反映与 之间函数关系的是( ).
B.
C D.
图1
图1
提示:当正方形与等腰直角三角形 的重合部分全部在 内部时,重合部分的面积即为正方形的面积,此时正
【答案】A
方形的边长随着 的增大而增大,对应的函数解析式为
,这一部分是开口向上的抛物线,只有选项A,B符合. 当重合部分是正方形 的一部分时,重合部分是一个矩形,且随着 的增大,这个矩形的长在增大,宽在减小,对应的函数解析式为 ,这一部分是开口向下的抛物线,故选项A符合.
2.(2024·重庆·中考)如图2,在中,,,为 上
一点,,过点作交于点.点,的距离为 ,
的周长与的周长之比为 .
图2
(1)请直接写出,分别关于的函数解析式,并写出自变量 的取值范围.
提示: , ,. ,. , 为上一点, .
图2
答案:,.
(2)在图3的平面直角坐标系中,画出函数, 的图象,并分别写出
函数, 的一条性质.
图3
解:函数,的图象如图138所示.
的图象性质:当时,随 的增大而增大.
的图象性质:当时,随 的增大而减小.
图138
(3)结合函数图象,请直接写出时 的取值范围(近似值保留小数点后一位,误差不超过 ).
图3
解:当时,的取值范围为 .
3.(2025·广西河池·模拟)如图4,已知是边长为 的等边三角形,动点,同时从,两点出发,分别沿, 匀速运动,其中点运动的速度是,点运动的速度是,当点到达点 时,,两点都停止运动.设运动时间为 ,解答下列问题:
图4
(1)设的面积为,求与 的函数解析式.
解:如图139,过点作于点.
由题意,得,.
是等边三角形, , .
,
,即 .
图139
(2)作交于点,连接,当为何值时, .
图4
解: , , .
是等边三角形.
.
,
.
图4
又 , 四边形是平行四边形.
.
又 , 四边形是矩形.
.
当时, ,又
, .
解得.
当 时, .
类型二 以函数知识为将背景的几何问题
图5
4.如图5,已知直线与轴、 轴分别交于
,两点,是以 为圆心,1为半径的圆上
一动点,连接,.则 面积的最大值是
( ).
A. B.
C.10.5 D.11.5
图140
提示:将代入,得 .故点B
的坐标为.令,则 ,解得
.故点A的坐标为.由此可得, ,
.在 中,由勾股定理,得
.如图140,过点C作 于点,连接 .
由三角形面积公式,得 ,即
.解得.上的点到直线 的最大
距离是.故面积的最大值是 .
【答案】C
5.(2024·江苏苏州·中考)如图6,中, ,, ,,反比例函数 的图象与交于点,与交于点 .
图6
(1)求, 的值.
解: ,,
,
, ,.
设直线 对应的函数解析式为,将, 代入,得
图6
解得
∴直线 对应的函数解析式为.
将点代入,得. 解得
.
将代入,得.解得 .
图6
(2)为反比例函数 图象上
一动点(点在点,之间运动,不与, 两点
重合),过点作,交轴于点,过点
作轴,交于点,连接,求
面积的最大值,并求出此时点 的坐标.
解:如图141,延长交轴于点,交于点 .
, , .
轴, , .
, .
图141
,即
.
设点的坐标为,, ,则,,
.
当 时,有最大值,为,此时点的坐标为, .
图141
6.(2025·广西贵港·模拟)在平面直角坐标系中,抛物线
与轴交于点和点(点在点 的左侧),
与轴交于点.若线段,,的长满足 ,则这样的
抛物线称为“黄金”抛物线.如图7,抛物线 为“黄
金”抛物线,其与轴的交点分别为点,点(其中点在点 的右侧),
与轴交于点,且 .
图7
备用图
(1)求抛物线 对应的函数解析式.
解:将代入,得
为“黄金”抛物线, .
又 ,
,
点在点 的右侧, ,.
将,代入 ,得
解得
该抛物线对应的函数解析式为 .
图7
(2)为上方抛物线上的动点,过点作 ,垂足为 .
图7
①求 的最大值.
图142
解:如图142,过点作轴于点,交 于点,则 ,
.
由(1)知,,∴ .
.
,即.
要使最大,只要 最大即可.
设直线对应的函数解析式为 ,将
,代入,得 解得
直线对应的函数解析式为 .
设,,则,,
为上方抛物线上的动点,∴
当时,有最大值,为
∴ 的最大值为 .
图142
②连接,当与相似时,求点 的坐标.
图143
解:当时,, 轴.
点与点的纵坐标相等,为2.将 代入,得 .
解得, 点的坐标为 .
当时, .
如图143,过点作轴于点,交于点
轴,
, .
在和 中, , ,,
.
设点的坐标为,,则 , .
,即
, .
则.
点的坐标为, .
综上所述,点的坐标为或, .
图143
同课章节目录
