2026年中考数学复习课件 专题五 四边形-第26讲 与圆有关的位置关系 (共62张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题五 四边形-第26讲 与圆有关的位置关系 (共62张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 00:00:00 | ||
图片预览











文档简介
(共62张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
第26讲 与圆有关的位置关系
聚焦核心
1.点与圆的位置关系
设圆的半径为,点到圆心的距离为 ,则点和圆的位置关系如下:
点在圆外___
点在圆上___
点在圆内___
点与圆的位置关系
2.直线与圆的位置关系
设圆的半径为,圆心到直线的距离为 ,则直线和圆的位置关系如下:
直线和圆相交___
直线和圆相切___
直线和圆相离___
直线与圆的位置关系
3.圆的切线
圆的 切线 定义 直线和圆仅有____个公共点(即直线和圆______)
时,这条直线叫作圆的切线,这个唯一的公共点叫作
______
性质 圆的切线垂直于过切点的______
判定 经过半径的______并且______于这条半径的直线是圆
的切线
一
相切
切点
半径
外端
垂直
切线 长 定义 从圆外一点作圆的切线,这点和______之间的线段的
长
定理 从圆外一点可以作出____条圆的切线,它们的切线长
______,这一点和圆心的连线______两条切线的夹角
切点
两
相等
平分
续表
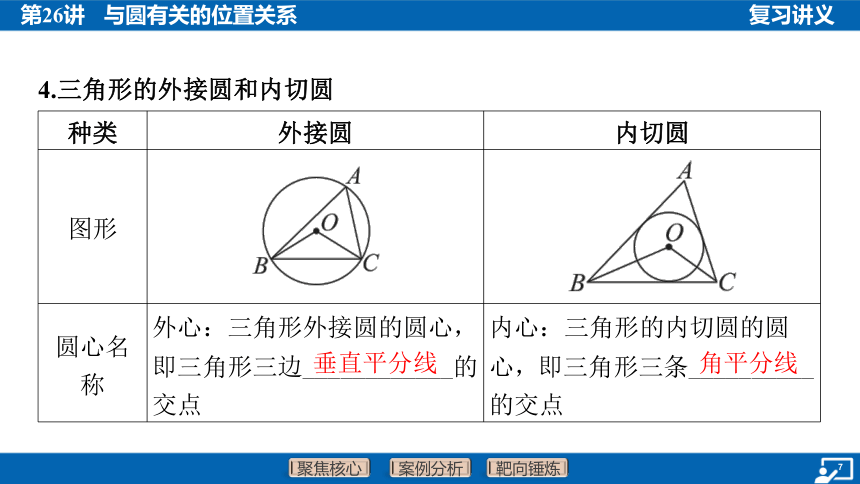
4.三角形的外接圆和内切圆
种类 外接圆 内切圆
图形 ___________________________________ _____________________________________________
圆心名 称 外心:三角形外接圆的圆心, 即三角形三边____________的 交点 内心:三角形的内切圆的圆
心,即三角形三条__________
的交点
垂直平分线
角平分线
种类 外接圆 内切圆
性质 三角形的外心到三角形三个顶 点的距离相等 三角形的内心到三角形三边的
距离相等
角度关 系
2
续表
第26讲 与圆有关的位置关系
案例分析
考点一 点与圆、直线与圆的位置关系
名师指导
判断点与圆、直线与圆的位置关系,关键是求出点与圆心、直线与
圆心的距离,然后与圆的半径进行比较,即可得出结论.
图1
例1 一题多问 如图1,在 中,
,,,为 的中点.
(1)以点为圆心,5为半径作,则点与 的位置关系是______
________.
点在上
图1
提示:在中, ,为 的中点,所以
.又因为的半径为5,所以点在 上.
思路点拨(1)只需求出的长,比较 的长与半径5的大小,即可得出结论.
(2)以点为圆心,为半径作,使点在内,点在 外,
则 的取值范围是___________.
图1
提示:因为点在内,点在外,所以 ,即
.
思路点拨 (2)根据点与圆的位置关系求半径的取值范围.由点在内,点 在外,得 .
思路点拨 (3)只需求出点到的距离,比较与半径 的大小,即可得解.
(3)以点为圆心,为半径作 .
图1
提示:如图40,过点作于点.在中, ,所以 .因为,所以 .
图40
①当时,直线与 的位置关系是______.
相交
【解析】因为,,所以.所以直线与 相交.
②当____时,直线与 相切.
【解析】当时,直线与 相切.
考点专练
1.若直线与半径为的有公共点,且点到直线的距离为6,则 的
取值范围是______.
2.(2025·广东广州·中考模拟)如图2,中,弦的长为,点 在
上,, .所在的平面内有一点 ,若
,则点与 的位置关系是( ).
图2
A.点在上 B.点在内 C.点在 外 D.无法确定
图2
提示:设与交于点D,因为弦的长为 ,
,所以 .因为
,所以 .所以
.所以.设 ,则
,在中, ,即
【答案】C
,解得(负值已舍去).所以 .因
为,所以.所以点在 外.
考点二 切线的性质
名师指导
当题目中有直线与圆相切的条件时,通常连接圆心和切点或过圆心
作切线的垂线,得到垂直,进而借助垂径定理、勾股定理、全等三角形、
相似三角形等知识,综合解决有关线段或角的问题.
图3
例2 (2024·甘肃临夏·中考)如图3,直线与
相切于点,为的直径,过点作 于
点,延长交直线于点 .
(1)求证:平分 .
思路点拨(1)欲证平分 ,则需证 .由已知条件无法直接得出这两角相等,则考虑作辅助线.已知为的切线, , 且已知切点,则连接 ,得到垂直.由垂直关系可得到平行关系,再结合平行线的性质、“等边对等角”即可得证.
图3
证明:连接
直线与相切于点, .
又 ,∴
,
平分 .
(2)已知,,求 的半径.
图3
解:设的半径为,则.
在中, ,,, .
解得
的半径为4.
思路点拨 (2)已知,,要求(半径)长,由切线的性质可知 是直角三角形,则根据勾股定理列出关于半径的方程,求解即可.
考点专练
图4
3.(2025·福建·中考模拟)如图4,已知点,在 上,
,直线与相切,切点为,且 为
的中点,则 的度数为( ).
A
A. B. C. D.
4.一题多问 如图5,与相切于点 .
图5
(1)若 ,则____ .
(2)若的半径为6,,则 ____.
(3)若 ,,则 _____.
65
10
考点三 切线的判定
名师指导 判定圆的切线的两种思路:
(1)若已知直线与圆的交点,则作出过该点的半径,证明直线与
该半径垂直,即“作半径,证垂直”;
(2)若不能确定直线与圆的交点,则过圆心作直线的垂线段,证
明垂线段的长等于半径,即“作垂直,证半径”.
图6
例3 (2025·榆林·中考模拟)如图6,平分, 与相切于点,延长交于点,过点 作,垂足为 .
(1)求证:是 的切线.
证明: 与相切于点, .
又 平分 ,,
是的半径.
是 的切线.
思路点拨(1)要证明是 的切线,只要证明由点向所作的垂线段是 的半径即可.由切线的性质知,是 的半径,因此需要证明 .
(2)已知的半径为4,,求 的长.
图6
解:(方法一) 的半径为4,
,, ,
∵ ,
,即.
解得 .
思路点拨 (2)由已知条件可求的长和 的长.所以求 的长有两个思路:思路一,利用 ,列比例式求解;思路二,在 中利用勾股定理,列方程求解.
图6
(方法二)设
,为的切线, .
同方法一知,,.在 中,由勾股定理,得,即.
解得 .
考点专练
5.如图7,点在上,点在外.下列条件不能判定是 的切
线的为( ).
D
图7
A. ,
B.
C.
D.与的交点是 的中点
图8
6.(2024·齐齐哈尔·模拟)如图8,已知经过 上
的点,.连接,分别交于点, ,
并且.延长交于点,连接 并延长交
于点 .
(1)求证:是 的切线.
证明:连接, ,, .
又 是 的半径, 是 的切线.
(2)已知,,求 的长.
图8
解:设, ,, , .
在R中, ,即.
解得
,
,,
,.
∴ ,.
∴ ,.
∴ .
图8
考点四 切线长定理
名师指导 切线长定理中的“钻石”图形:
如图9,,为 的切线,此图形是切线长定理的基本图形.
此图形含有如下元素:
(1)两个等腰三角形和 ;
(2)一条特殊的角平分线平分和 ;
(3)三对互相垂直的线段 .
图9
图10
例4 (2024·四川泸州·中考)如图10,,是 的
切线,切点为,,点,在 上.若
,则 的度数为( ).
A. B. C. D.
思路点拨
提示:连接.因为四边形是 的内接四边形,
所以 .因为
,所以 .因为 ,
是的切线,所以 .所以
.所以
.
答案:C
图10
考点专练
7.(2025·山东泰安·中考模拟)为了测量一个圆形光盘的半径,小明把直尺、
光盘和三角尺按图11所示放置于桌面上,并量出 ,则这张光
盘的半径约是____.(结果精确到,参考数据: )
图11
图41
提示:如图41,设光盘的圆心为 .由题意知,
,分别切于点,,连接, ,
.因为,分别为的切线,所以 为
的平分线,, .又
,所以
. 在 中,
, ,所以
.故这张光盘的半径约是
.
答案:6.9
考点五 三角形的内切圆与外接圆
名师指导 三角形内切圆的半径、外接圆的半径 的计算公式:
任意三角形的 内切圆 _________________________________________
直角三角形的 内切圆
直角三角形的 外接圆 _________________________________
等边三角形的 内切圆与外接 圆 ________________________________________
续表
图12
例5 传统文化(2025·湖南娄底·中考模拟)如图12,等边三
角形 内切的图形来自我国古代的太极图,等边三
角形内切圆中的黑色部分和白色部分关于等边三角形
的内心成中心对称,则圆中的黑色部分的面积与
的面积之比是( ).
A. B. C. D.
图12
思路点拨 可设的边长为,则 的内切圆
半径为,的高为,用含 的代数式表示
圆中黑色部分的面积和 的面积,再求出它们的
比值.
图12
提示:设的边长为,则的高为 .所以
的面积为 .因为圆内切于等边
三角形,所以圆的半径为 .所以圆中黑色部分
的面积为 .故圆中黑色部分的面积
与的面积之比是 .
【答案】A
考点专练
图13
8.(2025·山东聊城·中考改编)如图13,点是 外接圆
的圆心,点是的内心,连接, .若
,则 的度数为( ).
A. B. C. D.
图42
提示:如图42,连接.因为点是 的内心,所以平分.又因为 ,所以
.因为点是 外接圆的圆心,所以 .因为 ,所以 .
【答案】C
图14
9.教材变式[人教版九上第103页第14题变式]如
图14,为的内切圆,切点分别为 ,
,,且 ,, ,则
____.
图14
提示:(方法一)在 中,
.由为 的内切圆,
得,,.设 ,
则, .因为
,所以.解得.故 .
(方法二)同方法一得. 连接,.由为 的内切
圆,可证得四边形是正方形.则,即 的长为圆的半径长.
由直角三角形内切圆半径公式,得 .所以
.
10
第26讲 与圆有关的位置关系
靶向锤炼
靶向练
1.已知的半径为4, .下列四个图形中,正确的可能是( ).
B
A. B. C. D.
2.若的半径为,直线到圆心的距离为,则直线 与
的位置关系是( ).
C
A.相交 B.相切 C.相离 D.不能确定
图1
3.(2024·山西·中考)如图1,已知,以 为直径
的交于点,与相切于点,连接 .若
,则 的度数为( ).
D
A. B. C. D.
图2
4.如图2,为外一点,为的切线, 为切点,
交于点, ,,则线段 的长
为( ).
A
A.3 B. C.6 D.9
图3
5.如图3,,分别切于点,,切
于点,且分别交,于点,.若 ,则
的周长为( ).
C
A.5 B.7 C.12 D.10
提示:因为,分别切于点A,B, 切
于点,所以, ,
.故的周长为 .
图4
6.如图4,是的直径,交于点,
于点,要使是 的切线,还需补充一个条件,则
补充的条件不可能是( ).
A
A. B. C. D.
图5
7.以为中心点的量角器与直角三角尺 按如图5所示方式摆放,直角顶点 在零刻度线所在直线上,且量角器与三角尺只有一个公共点 ,若点处量角器的读数为 ,则 的度数是_________.
提示:连接.由题意知, , 是量角器所在半圆的切线,所以 .因为 ,所以 .故 .
图6
8.教材变式·一题多问[湘教版九下第74页例6变式]
如图6,已知 .
(1)求作:作的内切圆 .(保留作图痕迹,
无需写出作图过程)
【答案】如图55, 即为所求作.
图55
图6
(2)若 ,则_____ .
125
(3)若 ,则_________.(用含 的
代数式表示)
(4)若的内切圆的半径为, 的周长为
,则____.(用含, 的代数式表示)
图7
9.(2024·湖北武汉·中考节选)如图7, 为
等腰三角形,是底边的中点,腰 与半圆
相切于点,底边与半圆交于, 两点.
求证:与半圆 相切.
证明:如图56,连接,,过点 作于点
为等腰三角形, 是底边的中点, 平分.
因为与 相切于点, .
又,
是的半径.
与 的相切.
图56
攻坚练
图8
10.(2025·广西玉林·中考模拟)如图8,在网格中,各
小正方形的边长均为1,点,,,,, 均
在格点上,点是 的外心.在不添加其他字母
的情况下,除外,把你认为外心也是点 的三
角形都写出来:_______________________.
,,
图9
11.(2024·内蒙古包头·中考)如图9,四边形 是
的内接四边形,点在四边形内部,过点
作的切线交的延长线于点,连接, .若
, ,则 的度数为
______.
图9
提示:连接.由为的切线,得 ,即
.由此可得,
. 因为 ,所以
.因为 ,
,所以 ,从而得
.故 .
图10
12.(2024·四川眉山·中考)如图10,是 的直
径,点在上,点在 的延长线上,
,平分交于点 ,连接
.
(1)求证:是 的切线.
证明:如图57,连接
是的直径, .
.
,
,
.
∴ .
是的半径, 是 的切线.
图57
图10
(2)当,时,求 的长.
解: ,,∴
.
. .
如图57,连接, 平分,
.
是的直径, .
.
图57
拔尖练
图11
13.(2024·四川巴中·中考)如图11, 内接于
,为的中点,连接,,平分 交
于点,过点作交的延长线于点 .
(1)求证:是 的切线.
证明:如图58,连接
为的中点,
, .
又是的半径, 是 的切线.
(2)求证: .
图11
证明: 为的中点, .
平分,
,,
.
图58
(3)当,时,求 的长.
图11
解:如图59,连接
,, ,
,
,
四边形为的内接四边形, .
,
,即. .
图59
复习讲义
第一篇 考点精讲
专题六 圆
第26讲 与圆有关的位置关系
聚焦核心
1.点与圆的位置关系
设圆的半径为,点到圆心的距离为 ,则点和圆的位置关系如下:
点在圆外___
点在圆上___
点在圆内___
点与圆的位置关系
2.直线与圆的位置关系
设圆的半径为,圆心到直线的距离为 ,则直线和圆的位置关系如下:
直线和圆相交___
直线和圆相切___
直线和圆相离___
直线与圆的位置关系
3.圆的切线
圆的 切线 定义 直线和圆仅有____个公共点(即直线和圆______)
时,这条直线叫作圆的切线,这个唯一的公共点叫作
______
性质 圆的切线垂直于过切点的______
判定 经过半径的______并且______于这条半径的直线是圆
的切线
一
相切
切点
半径
外端
垂直
切线 长 定义 从圆外一点作圆的切线,这点和______之间的线段的
长
定理 从圆外一点可以作出____条圆的切线,它们的切线长
______,这一点和圆心的连线______两条切线的夹角
切点
两
相等
平分
续表
4.三角形的外接圆和内切圆
种类 外接圆 内切圆
图形 ___________________________________ _____________________________________________
圆心名 称 外心:三角形外接圆的圆心, 即三角形三边____________的 交点 内心:三角形的内切圆的圆
心,即三角形三条__________
的交点
垂直平分线
角平分线
种类 外接圆 内切圆
性质 三角形的外心到三角形三个顶 点的距离相等 三角形的内心到三角形三边的
距离相等
角度关 系
2
续表
第26讲 与圆有关的位置关系
案例分析
考点一 点与圆、直线与圆的位置关系
名师指导
判断点与圆、直线与圆的位置关系,关键是求出点与圆心、直线与
圆心的距离,然后与圆的半径进行比较,即可得出结论.
图1
例1 一题多问 如图1,在 中,
,,,为 的中点.
(1)以点为圆心,5为半径作,则点与 的位置关系是______
________.
点在上
图1
提示:在中, ,为 的中点,所以
.又因为的半径为5,所以点在 上.
思路点拨(1)只需求出的长,比较 的长与半径5的大小,即可得出结论.
(2)以点为圆心,为半径作,使点在内,点在 外,
则 的取值范围是___________.
图1
提示:因为点在内,点在外,所以 ,即
.
思路点拨 (2)根据点与圆的位置关系求半径的取值范围.由点在内,点 在外,得 .
思路点拨 (3)只需求出点到的距离,比较与半径 的大小,即可得解.
(3)以点为圆心,为半径作 .
图1
提示:如图40,过点作于点.在中, ,所以 .因为,所以 .
图40
①当时,直线与 的位置关系是______.
相交
【解析】因为,,所以.所以直线与 相交.
②当____时,直线与 相切.
【解析】当时,直线与 相切.
考点专练
1.若直线与半径为的有公共点,且点到直线的距离为6,则 的
取值范围是______.
2.(2025·广东广州·中考模拟)如图2,中,弦的长为,点 在
上,, .所在的平面内有一点 ,若
,则点与 的位置关系是( ).
图2
A.点在上 B.点在内 C.点在 外 D.无法确定
图2
提示:设与交于点D,因为弦的长为 ,
,所以 .因为
,所以 .所以
.所以.设 ,则
,在中, ,即
【答案】C
,解得(负值已舍去).所以 .因
为,所以.所以点在 外.
考点二 切线的性质
名师指导
当题目中有直线与圆相切的条件时,通常连接圆心和切点或过圆心
作切线的垂线,得到垂直,进而借助垂径定理、勾股定理、全等三角形、
相似三角形等知识,综合解决有关线段或角的问题.
图3
例2 (2024·甘肃临夏·中考)如图3,直线与
相切于点,为的直径,过点作 于
点,延长交直线于点 .
(1)求证:平分 .
思路点拨(1)欲证平分 ,则需证 .由已知条件无法直接得出这两角相等,则考虑作辅助线.已知为的切线, , 且已知切点,则连接 ,得到垂直.由垂直关系可得到平行关系,再结合平行线的性质、“等边对等角”即可得证.
图3
证明:连接
直线与相切于点, .
又 ,∴
,
平分 .
(2)已知,,求 的半径.
图3
解:设的半径为,则.
在中, ,,, .
解得
的半径为4.
思路点拨 (2)已知,,要求(半径)长,由切线的性质可知 是直角三角形,则根据勾股定理列出关于半径的方程,求解即可.
考点专练
图4
3.(2025·福建·中考模拟)如图4,已知点,在 上,
,直线与相切,切点为,且 为
的中点,则 的度数为( ).
A
A. B. C. D.
4.一题多问 如图5,与相切于点 .
图5
(1)若 ,则____ .
(2)若的半径为6,,则 ____.
(3)若 ,,则 _____.
65
10
考点三 切线的判定
名师指导 判定圆的切线的两种思路:
(1)若已知直线与圆的交点,则作出过该点的半径,证明直线与
该半径垂直,即“作半径,证垂直”;
(2)若不能确定直线与圆的交点,则过圆心作直线的垂线段,证
明垂线段的长等于半径,即“作垂直,证半径”.
图6
例3 (2025·榆林·中考模拟)如图6,平分, 与相切于点,延长交于点,过点 作,垂足为 .
(1)求证:是 的切线.
证明: 与相切于点, .
又 平分 ,,
是的半径.
是 的切线.
思路点拨(1)要证明是 的切线,只要证明由点向所作的垂线段是 的半径即可.由切线的性质知,是 的半径,因此需要证明 .
(2)已知的半径为4,,求 的长.
图6
解:(方法一) 的半径为4,
,, ,
∵ ,
,即.
解得 .
思路点拨 (2)由已知条件可求的长和 的长.所以求 的长有两个思路:思路一,利用 ,列比例式求解;思路二,在 中利用勾股定理,列方程求解.
图6
(方法二)设
,为的切线, .
同方法一知,,.在 中,由勾股定理,得,即.
解得 .
考点专练
5.如图7,点在上,点在外.下列条件不能判定是 的切
线的为( ).
D
图7
A. ,
B.
C.
D.与的交点是 的中点
图8
6.(2024·齐齐哈尔·模拟)如图8,已知经过 上
的点,.连接,分别交于点, ,
并且.延长交于点,连接 并延长交
于点 .
(1)求证:是 的切线.
证明:连接, ,, .
又 是 的半径, 是 的切线.
(2)已知,,求 的长.
图8
解:设, ,, , .
在R中, ,即.
解得
,
,,
,.
∴ ,.
∴ ,.
∴ .
图8
考点四 切线长定理
名师指导 切线长定理中的“钻石”图形:
如图9,,为 的切线,此图形是切线长定理的基本图形.
此图形含有如下元素:
(1)两个等腰三角形和 ;
(2)一条特殊的角平分线平分和 ;
(3)三对互相垂直的线段 .
图9
图10
例4 (2024·四川泸州·中考)如图10,,是 的
切线,切点为,,点,在 上.若
,则 的度数为( ).
A. B. C. D.
思路点拨
提示:连接.因为四边形是 的内接四边形,
所以 .因为
,所以 .因为 ,
是的切线,所以 .所以
.所以
.
答案:C
图10
考点专练
7.(2025·山东泰安·中考模拟)为了测量一个圆形光盘的半径,小明把直尺、
光盘和三角尺按图11所示放置于桌面上,并量出 ,则这张光
盘的半径约是____.(结果精确到,参考数据: )
图11
图41
提示:如图41,设光盘的圆心为 .由题意知,
,分别切于点,,连接, ,
.因为,分别为的切线,所以 为
的平分线,, .又
,所以
. 在 中,
, ,所以
.故这张光盘的半径约是
.
答案:6.9
考点五 三角形的内切圆与外接圆
名师指导 三角形内切圆的半径、外接圆的半径 的计算公式:
任意三角形的 内切圆 _________________________________________
直角三角形的 内切圆
直角三角形的 外接圆 _________________________________
等边三角形的 内切圆与外接 圆 ________________________________________
续表
图12
例5 传统文化(2025·湖南娄底·中考模拟)如图12,等边三
角形 内切的图形来自我国古代的太极图,等边三
角形内切圆中的黑色部分和白色部分关于等边三角形
的内心成中心对称,则圆中的黑色部分的面积与
的面积之比是( ).
A. B. C. D.
图12
思路点拨 可设的边长为,则 的内切圆
半径为,的高为,用含 的代数式表示
圆中黑色部分的面积和 的面积,再求出它们的
比值.
图12
提示:设的边长为,则的高为 .所以
的面积为 .因为圆内切于等边
三角形,所以圆的半径为 .所以圆中黑色部分
的面积为 .故圆中黑色部分的面积
与的面积之比是 .
【答案】A
考点专练
图13
8.(2025·山东聊城·中考改编)如图13,点是 外接圆
的圆心,点是的内心,连接, .若
,则 的度数为( ).
A. B. C. D.
图42
提示:如图42,连接.因为点是 的内心,所以平分.又因为 ,所以
.因为点是 外接圆的圆心,所以 .因为 ,所以 .
【答案】C
图14
9.教材变式[人教版九上第103页第14题变式]如
图14,为的内切圆,切点分别为 ,
,,且 ,, ,则
____.
图14
提示:(方法一)在 中,
.由为 的内切圆,
得,,.设 ,
则, .因为
,所以.解得.故 .
(方法二)同方法一得. 连接,.由为 的内切
圆,可证得四边形是正方形.则,即 的长为圆的半径长.
由直角三角形内切圆半径公式,得 .所以
.
10
第26讲 与圆有关的位置关系
靶向锤炼
靶向练
1.已知的半径为4, .下列四个图形中,正确的可能是( ).
B
A. B. C. D.
2.若的半径为,直线到圆心的距离为,则直线 与
的位置关系是( ).
C
A.相交 B.相切 C.相离 D.不能确定
图1
3.(2024·山西·中考)如图1,已知,以 为直径
的交于点,与相切于点,连接 .若
,则 的度数为( ).
D
A. B. C. D.
图2
4.如图2,为外一点,为的切线, 为切点,
交于点, ,,则线段 的长
为( ).
A
A.3 B. C.6 D.9
图3
5.如图3,,分别切于点,,切
于点,且分别交,于点,.若 ,则
的周长为( ).
C
A.5 B.7 C.12 D.10
提示:因为,分别切于点A,B, 切
于点,所以, ,
.故的周长为 .
图4
6.如图4,是的直径,交于点,
于点,要使是 的切线,还需补充一个条件,则
补充的条件不可能是( ).
A
A. B. C. D.
图5
7.以为中心点的量角器与直角三角尺 按如图5所示方式摆放,直角顶点 在零刻度线所在直线上,且量角器与三角尺只有一个公共点 ,若点处量角器的读数为 ,则 的度数是_________.
提示:连接.由题意知, , 是量角器所在半圆的切线,所以 .因为 ,所以 .故 .
图6
8.教材变式·一题多问[湘教版九下第74页例6变式]
如图6,已知 .
(1)求作:作的内切圆 .(保留作图痕迹,
无需写出作图过程)
【答案】如图55, 即为所求作.
图55
图6
(2)若 ,则_____ .
125
(3)若 ,则_________.(用含 的
代数式表示)
(4)若的内切圆的半径为, 的周长为
,则____.(用含, 的代数式表示)
图7
9.(2024·湖北武汉·中考节选)如图7, 为
等腰三角形,是底边的中点,腰 与半圆
相切于点,底边与半圆交于, 两点.
求证:与半圆 相切.
证明:如图56,连接,,过点 作于点
为等腰三角形, 是底边的中点, 平分.
因为与 相切于点, .
又,
是的半径.
与 的相切.
图56
攻坚练
图8
10.(2025·广西玉林·中考模拟)如图8,在网格中,各
小正方形的边长均为1,点,,,,, 均
在格点上,点是 的外心.在不添加其他字母
的情况下,除外,把你认为外心也是点 的三
角形都写出来:_______________________.
,,
图9
11.(2024·内蒙古包头·中考)如图9,四边形 是
的内接四边形,点在四边形内部,过点
作的切线交的延长线于点,连接, .若
, ,则 的度数为
______.
图9
提示:连接.由为的切线,得 ,即
.由此可得,
. 因为 ,所以
.因为 ,
,所以 ,从而得
.故 .
图10
12.(2024·四川眉山·中考)如图10,是 的直
径,点在上,点在 的延长线上,
,平分交于点 ,连接
.
(1)求证:是 的切线.
证明:如图57,连接
是的直径, .
.
,
,
.
∴ .
是的半径, 是 的切线.
图57
图10
(2)当,时,求 的长.
解: ,,∴
.
. .
如图57,连接, 平分,
.
是的直径, .
.
图57
拔尖练
图11
13.(2024·四川巴中·中考)如图11, 内接于
,为的中点,连接,,平分 交
于点,过点作交的延长线于点 .
(1)求证:是 的切线.
证明:如图58,连接
为的中点,
, .
又是的半径, 是 的切线.
(2)求证: .
图11
证明: 为的中点, .
平分,
,,
.
图58
(3)当,时,求 的长.
图11
解:如图59,连接
,, ,
,
,
四边形为的内接四边形, .
,
,即. .
图59
同课章节目录
