2024-2025学年北京二中教育集团八年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年北京二中教育集团八年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 08:00:51 | ||
图片预览


文档简介
2024-2025学年北京二中教育集团八年级(下)期末数学试卷
一、选择题(以下每题只有一个正确的选项,每小题2分,共16分)
1.(2分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.(2分)在 ABCD中,∠A=3∠B,则∠D的度数为( )
A.45° B.60° C.90° D.135°
3.(2分)如图,在数轴上找出表示3的点A,即OA=3,过点A作直线l垂直OA,在l上取点B,使AB=2,以原点O为圆心,OB为半径作弧,弧与数轴的交点C表示的实数是( )
A.4 B. C. D.
4.(2分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3).根据图象可知0<kx+b<3的解集为( )
A.x<0 B.x>1 C.x<0或x>1 D.0<x<1
5.(2分)如图,在边长为5的菱形ABCD中,AC=6,AH⊥BC于点H,则AH的长为( )
A.4 B.4.5 C.4.8 D.5
6.(2分)在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表所示:
成绩/米 1.70 1.75 1.80 1.85 1.90 1.95
人数 2 5 3 1
其中两个数据被污染了,根据这些数据,一定能确定这15名运动员成绩的( )
A.众数和中位数 B.中位数和方差
C.众数和方差 D.众数和平均数
7.(2分)下面的三个问题中都有两个变量:
①在压力F(N)一定的情况下,物体对地面的压强P(Pa)与受力面积S(m2);
②冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(℃)与冷冻时(t)(min);
③在弹性限度内,弹簧原长度为6cm,弹簧挂重物后的长度y(cm)与弹簧受到的拉力x(N).
其中,两个变量之间的函数关系是一次函数的是( )
A.①②③ B.②③ C.①③ D.①②
8.(2分)如图,在矩形ABCD中,点P是对角线AC上任意一点(不与A,C重合),过点P作EF∥AD,MN∥AB,点E,F,M,N分别是边AB,CD,AD,BC上的点.连接BP,DP.设AE=a,BE=b,AM=c,DM=d.下面四个结论中正确的个数是( )
①当AE=AM时,四边形AEPM是正方形;
②四边形BEPN与四边形DMPF的面积始终相等;
③;
④.
A.1个 B.2个 C.3个 D.4个
二、填空题(共16分,每题2分)
9.(2分)函数y中,自变量x的取值范围是 .
10.(2分)已知点A(2,y1)和点(3,y2)在直线y=﹣x+b上,则y1 y2.(填>、<、=)
11.(2分)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 .
甲 乙 丙 丁
平均数(cm) 192 195 195 193
方差 3.2 4.7 6.5 6.0
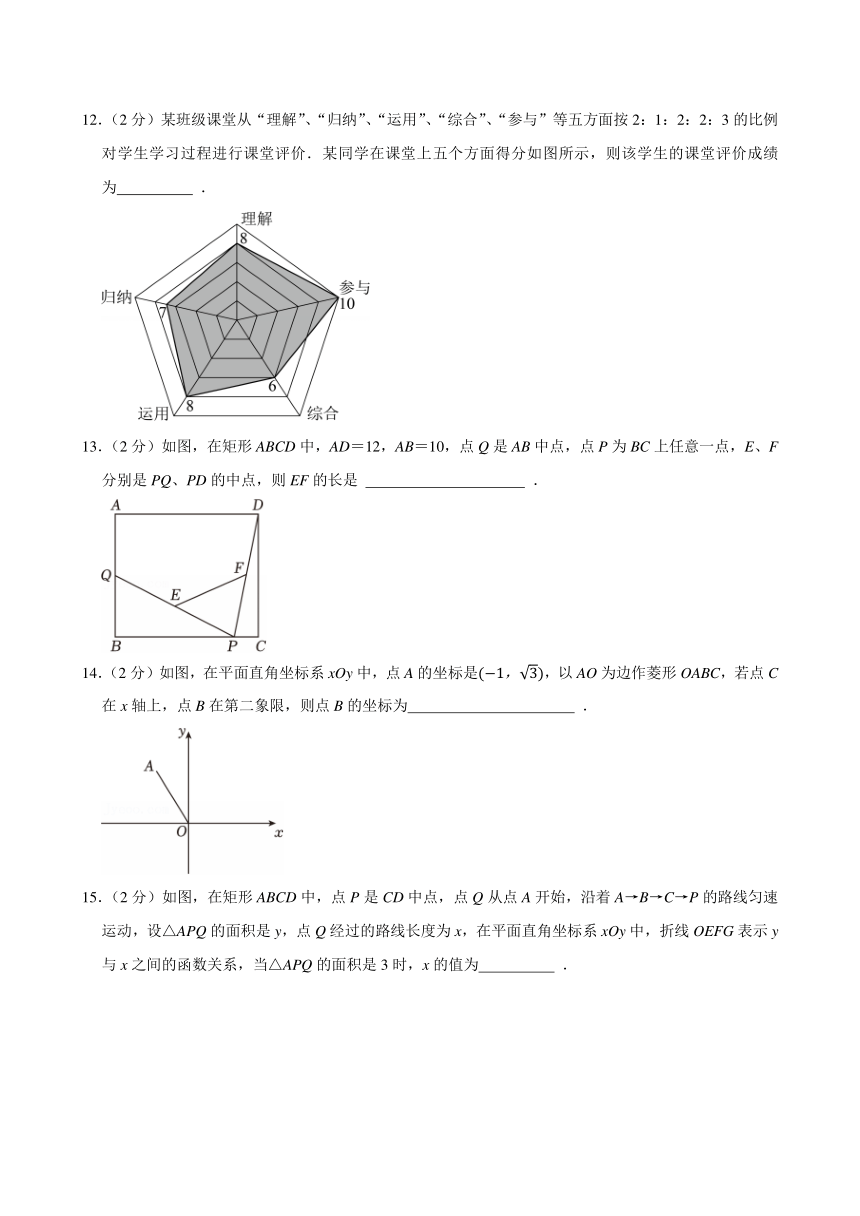
12.(2分)某班级课堂从“理解”、“归纳”、“运用”、“综合”、“参与”等五方面按2:1:2:2:3的比例对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 .
13.(2分)如图,在矩形ABCD中,AD=12,AB=10,点Q是AB中点,点P为BC上任意一点,E、F分别是PQ、PD的中点,则EF的长是 .
14.(2分)如图,在平面直角坐标系xOy中,点A的坐标是,以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,则点B的坐标为 .
15.(2分)如图,在矩形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,在平面直角坐标系xOy中,折线OEFG表示y与x之间的函数关系,当△APQ的面积是3时,x的值为 .
16.(2分)如图,已知AB=AC=3,∠BAC=90°,直线l是过点A的一条动直线(不与直线AB,AC重合),分别过点B,C作直线l的垂线,垂足为D,E.在直线l运动的过程中,DE的最大值为 .
三、解答题(共68分,其中第17-22题每题5分,第23-26题每题6分,第27-28题每题7分)
17.(5分)计算:.
18.(5分)计算:.
19.(5分)已知,如图,菱形ABCD的对角线AC,BD交于点O,
求作:矩形AOBE.
作法:①作AB的垂直平分线交AB于点F;
②连接OF并延长,在OF的延长线上截取点E,使EF=OF;
③连接AE,BE.
四边形AOBE为所求作的矩形.
(1)按要求利用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明:
证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形.( )(填推理依据)
∵四边形ABCD是菱形,
∴AC⊥BD,( )(填推理依据)
∴∠AOB=90°,
∴ AOBE是矩形.( )(填推理依据)
20.(5分)如图,小明家有一块三角形土地用来种植菠菜,其中AB=15m,AC=20m,BC=25m,小明想以B为起点挖一条水渠BD,点D在AC边上.水渠能将土地△ABC分成面积相等的两部分.分别用来种植两种不同蔬菜,又能同时对两种蔬菜进行灌溉.请帮小明计算一下水渠BD的准确长度.
21.(5分)如图,在 ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,求证:BM=DN.
22.(5分)共享电动车方便出行,是一种新理念下的交通工具.某天早上王老师想骑共享电动车去学校,有A,B两种品牌的共享电动车可选择.A,B两种品种共享电动车所收费用y(元)与骑行时间x(min)之间的函数图象如图所示.
(1)A品牌的共享电动车每分钟收费 元;骑行时间不超过10分钟时,B品牌的共享电动车一律收费 元.
(2)已知王老师家与学校的距离为4.5km,且王老师骑电动车的平均速度为300m/min,那么王老师选择哪种品牌的共享电动车会更省钱?求出此时使用两种品牌的共享电动车的价格差.
23.(6分)如图,在△ABC中,AB=BC,过A点作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)连接AC与BD交于点O,过点D作DE⊥BC交BC的延长线于E点,连接EO,若EO,BE=4,求CE的长.
24.(6分)在平面直角坐标系xOy中.一次函数y=kx+b的图象平行于,且经过点A(4,1).
(1)求一次函数解析式;
(2)点P为x轴上一点,一次函数y=kx+b的图象与x轴交于点B,△ABP的面积是2,求点P坐标;
(3)当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,直接写出m的取值范围.
25.(6分)百度推出了“文心一言”AI聊天机器人(以下简称甲款),抖音推出了“豆包”AI聊天机器人(以下简称乙款).有关人员开展了对甲,乙两数聊天机器人的使用满意度评分测验,并分别随机抽取20份评分数据.对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:A:60<x≤70,B:70<x≤80,C:80<x≤90,D:90<x≤100).
下面给出了部分信息:
甲款评分数据中的数据:64,70,75,76,78,78,80,82,84,85,85.85,90,90,94,95,98,98,99,100.
乙款评分数据中C组包含的所有数据:87,88,84,87,89,87,81,90.
甲、乙款评分统计表:
设备 平均数 中位数 众败
甲 86 85 a
乙 86
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= .m= .
(2)在此次测验中,有200人对甲款进行评分,220人对乙款进行评分.请通过计算,估计其中对甲、乙两款聊天机器人非常满意(90<x≤100)的用户总人数是多少?
(3)如果让你选择一款AI聊天机器人,你会选择哪一款?请利用数据说明理由.
26.(6分)请同学们探究函数y=2|x+1|﹣3的图象,通过列表、描点、画图,观察图象,并利用函数性质解决问题.
(1)画出函数y=2|x+1|﹣3的图象.
①列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 1 3 …
请补全表格:
②根据表格的数据,请在平面直角坐标系中描出对应点并连线,画出该函数图象.
(2)利用函数y=2|x+1|﹣3的图象,探索函数性质并解决问题:
①写出该函数的一条性质 ;
②当﹣2<x<2时,y的取值范围是 ;
③若点M(x1,y1)与N(x2,y2)是函数y=2|x+1|﹣3图象上的两个点,若对于﹣3≤x1≤0,a≤x2≤a+1,都有y1<y2,则a的取值范围是 .
27.(7分)如图,在正方形ABCD中,E为BC上一点(不与BC重合),过点C作CF⊥AE交AE延长线于点F,连接BF,作DG⊥FC交FC的延长线于点G.
(1)补全图形并用等式表示线段AF,CF,AD的数量关系并证明:
(2)用等式表示线段BF与CG的数量关系并证明.
2024-2025学年北京二中教育集团八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B D C A B B
一、选择题(以下每题只有一个正确的选项,每小题2分,共16分)
1.(2分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:根据最简二次根式的定义逐项分析判断如下:
A、,因16=42,可化简为4,不是最简二次根式;
B、,因27=9×3=32×3,不是最简二次根式;
C、,被开方数含分母,不是最简二次根式;
D、,被开方数10=2×5,无平方因数且不含分母,符合最简二次根式的条件;
故选:D.
2.(2分)在 ABCD中,∠A=3∠B,则∠D的度数为( )
A.45° B.60° C.90° D.135°
【解答】解:在平行四边形 ABCD中,∠A与∠B为邻角,故∠A+∠B=180°;
设∠B=x,则∠A=3x,代入得方程:3x+x=180°,
解得:x=45°,
因此,∠B=45°,∠A=3×45°=135°;
根据平行四边形对角相等,∠D=∠B=45°;
综上,∠D的度数为45°;
故选:A.
3.(2分)如图,在数轴上找出表示3的点A,即OA=3,过点A作直线l垂直OA,在l上取点B,使AB=2,以原点O为圆心,OB为半径作弧,弧与数轴的交点C表示的实数是( )
A.4 B. C. D.
【解答】解:由勾股定理得,OB,
∵以原点O为圆心,OB为半径作弧,弧与数轴的交点C,
∴OC=OB,
∴点C表示的实数是,
故选:B.
4.(2分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3).根据图象可知0<kx+b<3的解集为( )
A.x<0 B.x>1 C.x<0或x>1 D.0<x<1
【解答】解:∵一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3),
∴0<kx+b<3的解集0<x<1.
故选:D.
5.(2分)如图,在边长为5的菱形ABCD中,AC=6,AH⊥BC于点H,则AH的长为( )
A.4 B.4.5 C.4.8 D.5
【解答】解:∵四边形ABCD的边长为5,AC=6,
∴,OA⊥OB,AB=BC=5;
∴;
∵,
∴,
故选:C.
6.(2分)在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表所示:
成绩/米 1.70 1.75 1.80 1.85 1.90 1.95
人数 2 5 3 1
其中两个数据被污染了,根据这些数据,一定能确定这15名运动员成绩的( )
A.众数和中位数 B.中位数和方差
C.众数和方差 D.众数和平均数
【解答】解:根据题意可知:
被污染的数有4个,则众数是1.85,它出现了5次;
2+4<2+4+5,则中位数是第8个数据,中位数也是1.85,
根据以上数据,一定能确定这15名运动员成绩的众数与中位数;
故选:A.
7.(2分)下面的三个问题中都有两个变量:
①在压力F(N)一定的情况下,物体对地面的压强P(Pa)与受力面积S(m2);
②冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(℃)与冷冻时(t)(min);
③在弹性限度内,弹簧原长度为6cm,弹簧挂重物后的长度y(cm)与弹簧受到的拉力x(N).
其中,两个变量之间的函数关系是一次函数的是( )
A.①②③ B.②③ C.①③ D.①②
【解答】解:①压强P与受力面积S的关系为(F为定值),不符合一次函数的形式,不符合题意;
②温度T与时间t的关系为T=﹣2t(每分钟下降2℃),此式为T=﹣2t+0,符合一次函数y=kx+b的形式(b=0),符合题意;
③弹簧长度y与拉力x的关系为y=kx+6(k为弹性系数),符合一次函数的形式,符合题意;
综上,符合一次函数的是②③,
故选:B.
8.(2分)如图,在矩形ABCD中,点P是对角线AC上任意一点(不与A,C重合),过点P作EF∥AD,MN∥AB,点E,F,M,N分别是边AB,CD,AD,BC上的点.连接BP,DP.设AE=a,BE=b,AM=c,DM=d.下面四个结论中正确的个数是( )
①当AE=AM时,四边形AEPM是正方形;
②四边形BEPN与四边形DMPF的面积始终相等;
③;
④.
A.1个 B.2个 C.3个 D.4个
【解答】解:∵四边形ABCD是矩形,AE=a,BE=b,AM=c,DM=d,
∴∠BAD=90°,S△ABC=S△ADC,BC=AD=AM+DM=c+d,CD=AB=AE+BE=a+b;
∵EF∥AD,MN∥AB,
∴四边形AEPM是平行四边形(两组对边分别平行的四边形是平行四边形);
∵∠BAD=90°,
∴四边形AEPM是矩形(有一个角是直角的平行四边形是矩形),
∴PM=AE=a,PE=AM=c;
同理得四边形BEPN,四边形MPFD,四边形PNCF均是矩形;
∵AE=AM,
∴四边形AEPM是正方形(一组邻边相等的菱形是正方形);
故①正确;
∵S△AEP=S△AMP,S△PNC=S△PFC,S△ABC=S△ADC,
∴S△ABC﹣S△AEP﹣S△PNC=S△ADC﹣S△AMP﹣S△PFC,
即四边形BEPN与四边形DMPF的面积相等;
故②正确;
∵PE=AM=c,
∴;
在△BPE中,BE+PE>PB,
即;
故③错误;
连接BD,
∵,;
在△PBD中,PB+PD≥BD,当点P位于对角线BD上时,等号成立;
∴;
故④不正确;
综上,正确的有2个;
故选:B.
二、填空题(共16分,每题2分)
9.(2分)函数y中,自变量x的取值范围是 x .
【解答】解:由题意得:2x﹣1≥0,
解得:x,
故答案为:x.
10.(2分)已知点A(2,y1)和点(3,y2)在直线y=﹣x+b上,则y1 > y2.(填>、<、=)
【解答】解:由条件可知y随x增大而减小,
∵点A(2,y1)和点(3,y2)在直线y=﹣x+b上,且2<3,
∴y1>y2,
故答案为:>.
11.(2分)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 乙 .
甲 乙 丙 丁
平均数(cm) 192 195 195 193
方差 3.2 4.7 6.5 6.0
【解答】解:根据题意可知:从平均数角度看应该从乙、丙中选择一人参赛,
从方差来看,应该选择乙参赛,
故答案为:乙.
12.(2分)某班级课堂从“理解”、“归纳”、“运用”、“综合”、“参与”等五方面按2:1:2:2:3的比例对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 8.1 .
【解答】解:根据加权平均数的计算方法可得:
,
故答案为:8.1.
13.(2分)如图,在矩形ABCD中,AD=12,AB=10,点Q是AB中点,点P为BC上任意一点,E、F分别是PQ、PD的中点,则EF的长是 .
【解答】解:连接DQ,
∵四边形ABCD是矩形,
∴∠A=90°,
∵Q是AB的中点,AB=10,AD=12,
∴,
∴,
∵E、F分别是PQ、PD的中点,
∴EF为△PDQ的中位线,
∴,
故答案为:.
14.(2分)如图,在平面直角坐标系xOy中,点A的坐标是,以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,则点B的坐标为 .
【解答】解:∵以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,
∴只有一种情况,如图所示:
延长BA交y轴于点E,
∴BE⊥y轴,
∵点A的坐标是,
∴,
∴,
∴AO=AB=2,
∴BE=3,
∵点B在第二象限,
∴,
故答案为:.
15.(2分)如图,在矩形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,在平面直角坐标系xOy中,折线OEFG表示y与x之间的函数关系,当△APQ的面积是3时,x的值为 2或7 .
【解答】解:由函数图象可得,AB=4,S△ABP=6,
∵四边形ABCD是矩形,
∴AB=CD=4,∠ABC=90°,
∴,
∴BC=3;
由条件可知;
当点Q在AB上,且y的值为3时,则,解得x=2;
当点Q在BC上,且y的值为3时,则,解得x=7;
当点Q在CD上,且y的值为3时,则,解得x=7;
综上所述,x的值为2或7,
故答案为:2或7.
16.(2分)如图,已知AB=AC=3,∠BAC=90°,直线l是过点A的一条动直线(不与直线AB,AC重合),分别过点B,C作直线l的垂线,垂足为D,E.在直线l运动的过程中,DE的最大值为 .
【解答】解:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵过点B,C作直线的垂线,垂足为D,E,
∴∠BDA=∠CEA=90°,
∴∠BAD+∠B=90°,
∴∠CAE=∠B,
∵AB=AC=3,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,如图,
当直线l在∠BAC 内部时,D1E1=AD1﹣AE1,
当直线l在∠BAC外部时,D2E2=AD2+AE2,
∴DE 的值最大时,直线l在∠BAC 外部,
设AD2=CE2=x,BD2=AE2=y,
∴D2E2=AD2+AE2=x+y,
∵AB=AC=3,
∴x2+y2=32=9,
∵(x﹣y)2≥0,
∴x2+y2﹣2xy≥0,即2xy≤9,
∴(x+y)2=x2+y2+2xy=9+2xy≤18,
∵BD+AD>AB,
∴,
∴DE的最大值为,
故答案为:.
三、解答题(共68分,其中第17-22题每题5分,第23-26题每题6分,第27-28题每题7分)
17.(5分)计算:.
【解答】解:原式
.
18.(5分)计算:.
【解答】解:原式=3
=6
=5.
19.(5分)已知,如图,菱形ABCD的对角线AC,BD交于点O,
求作:矩形AOBE.
作法:①作AB的垂直平分线交AB于点F;
②连接OF并延长,在OF的延长线上截取点E,使EF=OF;
③连接AE,BE.
四边形AOBE为所求作的矩形.
(1)按要求利用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明:
证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形.( 对角线互相平分的四边形为平行四边形 )(填推理依据)
∵四边形ABCD是菱形,
∴AC⊥BD,( 菱形的对角线互相垂直平分 )(填推理依据)
∴∠AOB=90°,
∴ AOBE是矩形.( 有一个内角为90°的平行四边形为矩形 )(填推理依据)
【解答】(1)解:如图,四边形AOBE为所;
(2)证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形(对角线互相平分的四边形为平行四边形),
∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直平分),
∴∠AOB=90°,
∴ AOBE是矩形(有一个内角为90°的平行四边形为矩形).
故答案为:对角线互相平分的四边形为平行四边形,菱形的对角线互相垂直平分,有一个内角为90°的平行四边形为矩形.
20.(5分)如图,小明家有一块三角形土地用来种植菠菜,其中AB=15m,AC=20m,BC=25m,小明想以B为起点挖一条水渠BD,点D在AC边上.水渠能将土地△ABC分成面积相等的两部分.分别用来种植两种不同蔬菜,又能同时对两种蔬菜进行灌溉.请帮小明计算一下水渠BD的准确长度.
【解答】解:∵AB=15m,AC=20m,BC=25m,
∴AB2+AC2=152+202=225+400=625,BC2=252=625,
∴AB2+AC2=BC2,
∴三角形ABC是直角三角形,∠A=90°,
∵BD平分△ABC的面积,
∴BD是△ABC中线,
∴ADAC=10m,
在直角三角形ABD中,由勾股定理得:BD5(m),
答:水渠BD的准确长度为m.
21.(5分)如图,在 ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,求证:BM=DN.
【解答】证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠BAM=∠DCN,
又在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS),
∴BM=DN.
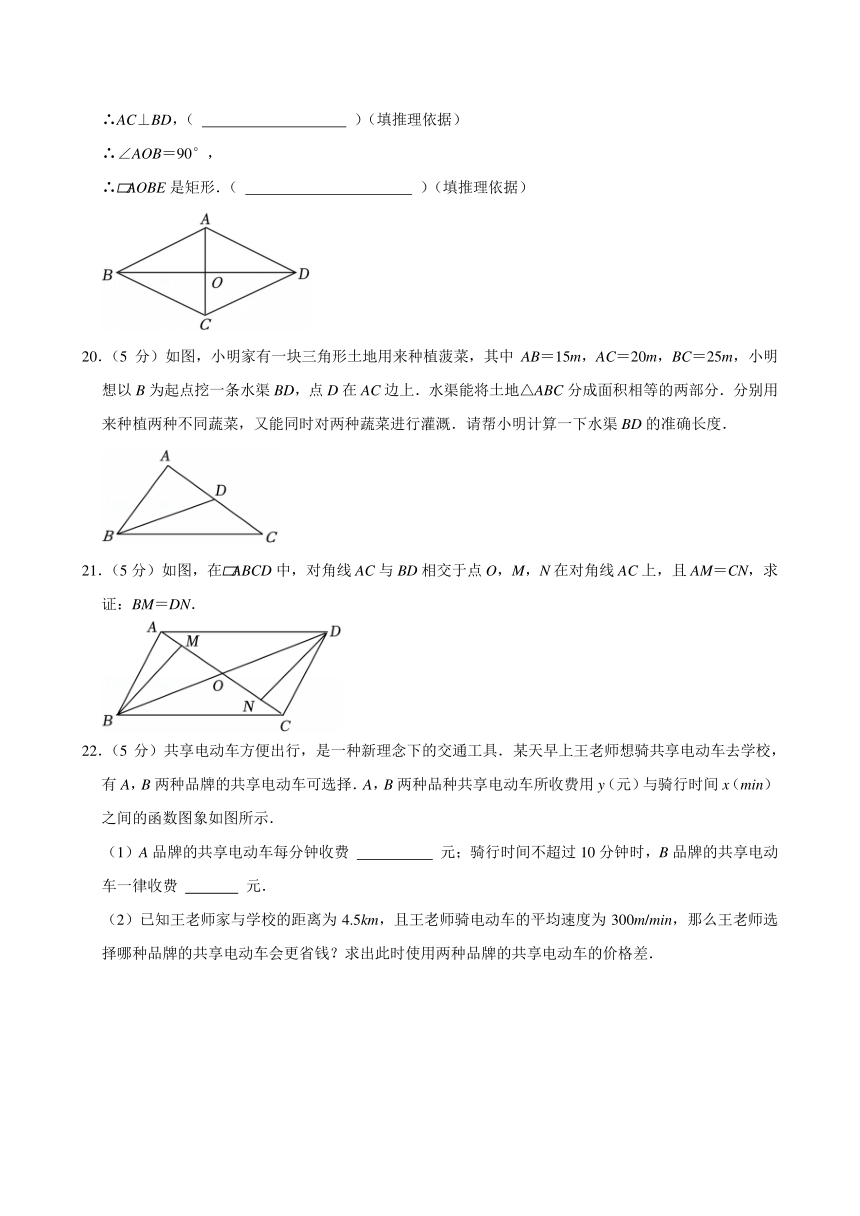
22.(5分)共享电动车方便出行,是一种新理念下的交通工具.某天早上王老师想骑共享电动车去学校,有A,B两种品牌的共享电动车可选择.A,B两种品种共享电动车所收费用y(元)与骑行时间x(min)之间的函数图象如图所示.
(1)A品牌的共享电动车每分钟收费 0.4 元;骑行时间不超过10分钟时,B品牌的共享电动车一律收费 6 元.
(2)已知王老师家与学校的距离为4.5km,且王老师骑电动车的平均速度为300m/min,那么王老师选择哪种品牌的共享电动车会更省钱?求出此时使用两种品牌的共享电动车的价格差.
【解答】解:(1)根据图象得:8÷20=0.4元,
骑行时间不超过10分钟时,B品牌的共享电动车一律收费6元,
故答案为:0.4;6;
(2)选择B品牌共享电动车会更省钱.理由如下:
王老师从家骑行到学校所需时间为,
观察函数图象可知,当x=15时,yA<yB,
所以选择A品牌共享电动车会更省钱,
设yA=kx,将点(20,8)代入得:8=20k,
解得:k=0.4,
∴yA=0.4x,
设yB=mx+n,由条件可得:,
解得:,
∴yB=0.2x+4,
当x=15时,yA=6,yB=7,
yB﹣yA=1元.
23.(6分)如图,在△ABC中,AB=BC,过A点作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)连接AC与BD交于点O,过点D作DE⊥BC交BC的延长线于E点,连接EO,若EO,BE=4,求CE的长.
【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠ADB,
∴AB=AD,
∵AB=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴BO=DO,BC=CD,
∵DE⊥BC,
∴∠BED=90°,
∴,
∴,
设CE=x,则BC=CD=BE﹣CE=4﹣x,
在Rt△CDE中,由勾股定理得CD2=CE2+DE2,
∴(4﹣x)2=x2+22,
解得:,
∴CE的长为.
24.(6分)在平面直角坐标系xOy中.一次函数y=kx+b的图象平行于,且经过点A(4,1).
(1)求一次函数解析式;
(2)点P为x轴上一点,一次函数y=kx+b的图象与x轴交于点B,△ABP的面积是2,求点P坐标;
(3)当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,直接写出m的取值范围.
【解答】解:(1)∵一次函数y=kx+b的图象平行于直线y,
∴k,
把A(4,1)代入yx+b得,b=﹣1,
∴一次函数的表达式为:yx﹣1;
(2)令yx﹣1中y=0,则x=2,
∴B(2,0),
设点P的坐标为(n,0),则BP=|n﹣2|,
∵△ABP的面积是2,
∴BP yA2,
解得:n=6或n=﹣2,
∴点P坐标为(6,0)或(﹣2,0).
(3)如图:
,
把x=1代入y,求得y,
把(1,)代入y=m(x+1)(m≠0)得,2m,
解得m,
∵当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,
∴m的取值范围是m且m≠0.
25.(6分)百度推出了“文心一言”AI聊天机器人(以下简称甲款),抖音推出了“豆包”AI聊天机器人(以下简称乙款).有关人员开展了对甲,乙两数聊天机器人的使用满意度评分测验,并分别随机抽取20份评分数据.对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:A:60<x≤70,B:70<x≤80,C:80<x≤90,D:90<x≤100).
下面给出了部分信息:
甲款评分数据中的数据:64,70,75,76,78,78,80,82,84,85,85.85,90,90,94,95,98,98,99,100.
乙款评分数据中C组包含的所有数据:87,88,84,87,89,87,81,90.
甲、乙款评分统计表:
设备 平均数 中位数 众败
甲 86 85 a
乙 86
根据以上信息,解答下列问题:
(1)上述图表中a= 85 ,b= 85.5 .m= 20 .
(2)在此次测验中,有200人对甲款进行评分,220人对乙款进行评分.请通过计算,估计其中对甲、乙两款聊天机器人非常满意(90<x≤100)的用户总人数是多少?
(3)如果让你选择一款AI聊天机器人,你会选择哪一款?请利用数据说明理由.
【解答】解:(1)甲款评分数据中,85分出现次数最多,则a=85,
A组B组共有20×(10%+30%)=8人,
将C组包含的所有数据排序为:81,84,87,87,87,88,89,90,
第十个和第十一个评分分别为84、87,
所以中位数.
乙款聊天机器人中,C组包含8个数据,所占比例为,
∴m%=1﹣40%﹣10%﹣30%=20%,
∴m=20,
故答案为:85,85.5;20;
(2)D组有20×20%=4人,
甲数据中D组有6人,
∴非常满意用户总人数人.
(3)甲乙款平均数都相同,但是乙的中位数85.5,甲的中位数85,
∴选择乙款聊天机器人.
26.(6分)请同学们探究函数y=2|x+1|﹣3的图象,通过列表、描点、画图,观察图象,并利用函数性质解决问题.
(1)画出函数y=2|x+1|﹣3的图象.
①列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 1 3 …
请补全表格:
②根据表格的数据,请在平面直角坐标系中描出对应点并连线,画出该函数图象.
(2)利用函数y=2|x+1|﹣3的图象,探索函数性质并解决问题:
①写出该函数的一条性质 函数图象关于x=﹣1对称(答案不唯一) ;
②当﹣2<x<2时,y的取值范围是 ﹣3≤y<3 ;
③若点M(x1,y1)与N(x2,y2)是函数y=2|x+1|﹣3图象上的两个点,若对于﹣3≤x1≤0,a≤x2≤a+1,都有y1<y2,则a的取值范围是 a>1或a<﹣4 .
【解答】解:(1)①当x=﹣2时,y=2×|﹣2+1|﹣3=﹣1,
当x=﹣1时,y=2×|﹣1+1|﹣3=﹣3,
补全表格如下:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 ﹣3 ﹣1 1 3 …
②函数图象如图所示:
(2)①函数图象关于x=﹣1对称(答案不唯一),
故答案为:函数图象关于x=﹣1对称;
②由函数图象得,当﹣2<x<2时,﹣3≤y<3,
故答案为:﹣3≤y<3;
③∵﹣3≤x1≤0,
∴﹣3≤y1≤1,
结合图象得:a>1或a<﹣4,
故答案为:a>1或a<﹣4.
27.(7分)如图,在正方形ABCD中,E为BC上一点(不与BC重合),过点C作CF⊥AE交AE延长线于点F,连接BF,作DG⊥FC交FC的延长线于点G.
(1)补全图形并用等式表示线段AF,CF,AD的数量关系并证明:
(2)用等式表示线段BF与CG的数量关系并证明.
【解答】(1)解:补全图形如下:
连接AC,
∵四边形ABCD是正方形,
∴AD=CD,
∵CF⊥AE,
∴AF2+CF2=AC2=2AD2,
∴AF2+CF2=2AD2;
(2)过点B作BH⊥AF于点H,过点B作BM⊥CF于点M,如图所示:
∴∠AHB=∠BMC=90°,
∴∠ABH+∠CBH=90°,
∵CF⊥AE,
∴四边形BMFH为矩形,
∴∠HBM=90°,
∴∠ABH=∠MBC,
∵四边形ABCD是正方形,
∴AB=BC,
∴△ABH≌△CBM(AAS),
同理得:△DCG≌△CBM(AAS),
∴△ABH≌△CBM≌△DCG,
∴BH=CG=BM,
∴四边形BMFH为正方形,
∴.
一、选择题(以下每题只有一个正确的选项,每小题2分,共16分)
1.(2分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.(2分)在 ABCD中,∠A=3∠B,则∠D的度数为( )
A.45° B.60° C.90° D.135°
3.(2分)如图,在数轴上找出表示3的点A,即OA=3,过点A作直线l垂直OA,在l上取点B,使AB=2,以原点O为圆心,OB为半径作弧,弧与数轴的交点C表示的实数是( )
A.4 B. C. D.
4.(2分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3).根据图象可知0<kx+b<3的解集为( )
A.x<0 B.x>1 C.x<0或x>1 D.0<x<1
5.(2分)如图,在边长为5的菱形ABCD中,AC=6,AH⊥BC于点H,则AH的长为( )
A.4 B.4.5 C.4.8 D.5
6.(2分)在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表所示:
成绩/米 1.70 1.75 1.80 1.85 1.90 1.95
人数 2 5 3 1
其中两个数据被污染了,根据这些数据,一定能确定这15名运动员成绩的( )
A.众数和中位数 B.中位数和方差
C.众数和方差 D.众数和平均数
7.(2分)下面的三个问题中都有两个变量:
①在压力F(N)一定的情况下,物体对地面的压强P(Pa)与受力面积S(m2);
②冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(℃)与冷冻时(t)(min);
③在弹性限度内,弹簧原长度为6cm,弹簧挂重物后的长度y(cm)与弹簧受到的拉力x(N).
其中,两个变量之间的函数关系是一次函数的是( )
A.①②③ B.②③ C.①③ D.①②
8.(2分)如图,在矩形ABCD中,点P是对角线AC上任意一点(不与A,C重合),过点P作EF∥AD,MN∥AB,点E,F,M,N分别是边AB,CD,AD,BC上的点.连接BP,DP.设AE=a,BE=b,AM=c,DM=d.下面四个结论中正确的个数是( )
①当AE=AM时,四边形AEPM是正方形;
②四边形BEPN与四边形DMPF的面积始终相等;
③;
④.
A.1个 B.2个 C.3个 D.4个
二、填空题(共16分,每题2分)
9.(2分)函数y中,自变量x的取值范围是 .
10.(2分)已知点A(2,y1)和点(3,y2)在直线y=﹣x+b上,则y1 y2.(填>、<、=)
11.(2分)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 .
甲 乙 丙 丁
平均数(cm) 192 195 195 193
方差 3.2 4.7 6.5 6.0
12.(2分)某班级课堂从“理解”、“归纳”、“运用”、“综合”、“参与”等五方面按2:1:2:2:3的比例对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 .
13.(2分)如图,在矩形ABCD中,AD=12,AB=10,点Q是AB中点,点P为BC上任意一点,E、F分别是PQ、PD的中点,则EF的长是 .
14.(2分)如图,在平面直角坐标系xOy中,点A的坐标是,以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,则点B的坐标为 .
15.(2分)如图,在矩形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,在平面直角坐标系xOy中,折线OEFG表示y与x之间的函数关系,当△APQ的面积是3时,x的值为 .
16.(2分)如图,已知AB=AC=3,∠BAC=90°,直线l是过点A的一条动直线(不与直线AB,AC重合),分别过点B,C作直线l的垂线,垂足为D,E.在直线l运动的过程中,DE的最大值为 .
三、解答题(共68分,其中第17-22题每题5分,第23-26题每题6分,第27-28题每题7分)
17.(5分)计算:.
18.(5分)计算:.
19.(5分)已知,如图,菱形ABCD的对角线AC,BD交于点O,
求作:矩形AOBE.
作法:①作AB的垂直平分线交AB于点F;
②连接OF并延长,在OF的延长线上截取点E,使EF=OF;
③连接AE,BE.
四边形AOBE为所求作的矩形.
(1)按要求利用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明:
证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形.( )(填推理依据)
∵四边形ABCD是菱形,
∴AC⊥BD,( )(填推理依据)
∴∠AOB=90°,
∴ AOBE是矩形.( )(填推理依据)
20.(5分)如图,小明家有一块三角形土地用来种植菠菜,其中AB=15m,AC=20m,BC=25m,小明想以B为起点挖一条水渠BD,点D在AC边上.水渠能将土地△ABC分成面积相等的两部分.分别用来种植两种不同蔬菜,又能同时对两种蔬菜进行灌溉.请帮小明计算一下水渠BD的准确长度.
21.(5分)如图,在 ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,求证:BM=DN.
22.(5分)共享电动车方便出行,是一种新理念下的交通工具.某天早上王老师想骑共享电动车去学校,有A,B两种品牌的共享电动车可选择.A,B两种品种共享电动车所收费用y(元)与骑行时间x(min)之间的函数图象如图所示.
(1)A品牌的共享电动车每分钟收费 元;骑行时间不超过10分钟时,B品牌的共享电动车一律收费 元.
(2)已知王老师家与学校的距离为4.5km,且王老师骑电动车的平均速度为300m/min,那么王老师选择哪种品牌的共享电动车会更省钱?求出此时使用两种品牌的共享电动车的价格差.
23.(6分)如图,在△ABC中,AB=BC,过A点作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)连接AC与BD交于点O,过点D作DE⊥BC交BC的延长线于E点,连接EO,若EO,BE=4,求CE的长.
24.(6分)在平面直角坐标系xOy中.一次函数y=kx+b的图象平行于,且经过点A(4,1).
(1)求一次函数解析式;
(2)点P为x轴上一点,一次函数y=kx+b的图象与x轴交于点B,△ABP的面积是2,求点P坐标;
(3)当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,直接写出m的取值范围.
25.(6分)百度推出了“文心一言”AI聊天机器人(以下简称甲款),抖音推出了“豆包”AI聊天机器人(以下简称乙款).有关人员开展了对甲,乙两数聊天机器人的使用满意度评分测验,并分别随机抽取20份评分数据.对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:A:60<x≤70,B:70<x≤80,C:80<x≤90,D:90<x≤100).
下面给出了部分信息:
甲款评分数据中的数据:64,70,75,76,78,78,80,82,84,85,85.85,90,90,94,95,98,98,99,100.
乙款评分数据中C组包含的所有数据:87,88,84,87,89,87,81,90.
甲、乙款评分统计表:
设备 平均数 中位数 众败
甲 86 85 a
乙 86
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= .m= .
(2)在此次测验中,有200人对甲款进行评分,220人对乙款进行评分.请通过计算,估计其中对甲、乙两款聊天机器人非常满意(90<x≤100)的用户总人数是多少?
(3)如果让你选择一款AI聊天机器人,你会选择哪一款?请利用数据说明理由.
26.(6分)请同学们探究函数y=2|x+1|﹣3的图象,通过列表、描点、画图,观察图象,并利用函数性质解决问题.
(1)画出函数y=2|x+1|﹣3的图象.
①列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 1 3 …
请补全表格:
②根据表格的数据,请在平面直角坐标系中描出对应点并连线,画出该函数图象.
(2)利用函数y=2|x+1|﹣3的图象,探索函数性质并解决问题:
①写出该函数的一条性质 ;
②当﹣2<x<2时,y的取值范围是 ;
③若点M(x1,y1)与N(x2,y2)是函数y=2|x+1|﹣3图象上的两个点,若对于﹣3≤x1≤0,a≤x2≤a+1,都有y1<y2,则a的取值范围是 .
27.(7分)如图,在正方形ABCD中,E为BC上一点(不与BC重合),过点C作CF⊥AE交AE延长线于点F,连接BF,作DG⊥FC交FC的延长线于点G.
(1)补全图形并用等式表示线段AF,CF,AD的数量关系并证明:
(2)用等式表示线段BF与CG的数量关系并证明.
2024-2025学年北京二中教育集团八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B D C A B B
一、选择题(以下每题只有一个正确的选项,每小题2分,共16分)
1.(2分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【解答】解:根据最简二次根式的定义逐项分析判断如下:
A、,因16=42,可化简为4,不是最简二次根式;
B、,因27=9×3=32×3,不是最简二次根式;
C、,被开方数含分母,不是最简二次根式;
D、,被开方数10=2×5,无平方因数且不含分母,符合最简二次根式的条件;
故选:D.
2.(2分)在 ABCD中,∠A=3∠B,则∠D的度数为( )
A.45° B.60° C.90° D.135°
【解答】解:在平行四边形 ABCD中,∠A与∠B为邻角,故∠A+∠B=180°;
设∠B=x,则∠A=3x,代入得方程:3x+x=180°,
解得:x=45°,
因此,∠B=45°,∠A=3×45°=135°;
根据平行四边形对角相等,∠D=∠B=45°;
综上,∠D的度数为45°;
故选:A.
3.(2分)如图,在数轴上找出表示3的点A,即OA=3,过点A作直线l垂直OA,在l上取点B,使AB=2,以原点O为圆心,OB为半径作弧,弧与数轴的交点C表示的实数是( )
A.4 B. C. D.
【解答】解:由勾股定理得,OB,
∵以原点O为圆心,OB为半径作弧,弧与数轴的交点C,
∴OC=OB,
∴点C表示的实数是,
故选:B.
4.(2分)如图,在平面直角坐标系xOy中,一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3).根据图象可知0<kx+b<3的解集为( )
A.x<0 B.x>1 C.x<0或x>1 D.0<x<1
【解答】解:∵一次函数y=kx+b(k、b是常数,k≠0)的图象与x轴交于点A(1,0),与y轴交于点B(0,3),
∴0<kx+b<3的解集0<x<1.
故选:D.
5.(2分)如图,在边长为5的菱形ABCD中,AC=6,AH⊥BC于点H,则AH的长为( )
A.4 B.4.5 C.4.8 D.5
【解答】解:∵四边形ABCD的边长为5,AC=6,
∴,OA⊥OB,AB=BC=5;
∴;
∵,
∴,
故选:C.
6.(2分)在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表所示:
成绩/米 1.70 1.75 1.80 1.85 1.90 1.95
人数 2 5 3 1
其中两个数据被污染了,根据这些数据,一定能确定这15名运动员成绩的( )
A.众数和中位数 B.中位数和方差
C.众数和方差 D.众数和平均数
【解答】解:根据题意可知:
被污染的数有4个,则众数是1.85,它出现了5次;
2+4<2+4+5,则中位数是第8个数据,中位数也是1.85,
根据以上数据,一定能确定这15名运动员成绩的众数与中位数;
故选:A.
7.(2分)下面的三个问题中都有两个变量:
①在压力F(N)一定的情况下,物体对地面的压强P(Pa)与受力面积S(m2);
②冷冻一个0℃的物体,使它每分钟下降2℃,物体的温度T(℃)与冷冻时(t)(min);
③在弹性限度内,弹簧原长度为6cm,弹簧挂重物后的长度y(cm)与弹簧受到的拉力x(N).
其中,两个变量之间的函数关系是一次函数的是( )
A.①②③ B.②③ C.①③ D.①②
【解答】解:①压强P与受力面积S的关系为(F为定值),不符合一次函数的形式,不符合题意;
②温度T与时间t的关系为T=﹣2t(每分钟下降2℃),此式为T=﹣2t+0,符合一次函数y=kx+b的形式(b=0),符合题意;
③弹簧长度y与拉力x的关系为y=kx+6(k为弹性系数),符合一次函数的形式,符合题意;
综上,符合一次函数的是②③,
故选:B.
8.(2分)如图,在矩形ABCD中,点P是对角线AC上任意一点(不与A,C重合),过点P作EF∥AD,MN∥AB,点E,F,M,N分别是边AB,CD,AD,BC上的点.连接BP,DP.设AE=a,BE=b,AM=c,DM=d.下面四个结论中正确的个数是( )
①当AE=AM时,四边形AEPM是正方形;
②四边形BEPN与四边形DMPF的面积始终相等;
③;
④.
A.1个 B.2个 C.3个 D.4个
【解答】解:∵四边形ABCD是矩形,AE=a,BE=b,AM=c,DM=d,
∴∠BAD=90°,S△ABC=S△ADC,BC=AD=AM+DM=c+d,CD=AB=AE+BE=a+b;
∵EF∥AD,MN∥AB,
∴四边形AEPM是平行四边形(两组对边分别平行的四边形是平行四边形);
∵∠BAD=90°,
∴四边形AEPM是矩形(有一个角是直角的平行四边形是矩形),
∴PM=AE=a,PE=AM=c;
同理得四边形BEPN,四边形MPFD,四边形PNCF均是矩形;
∵AE=AM,
∴四边形AEPM是正方形(一组邻边相等的菱形是正方形);
故①正确;
∵S△AEP=S△AMP,S△PNC=S△PFC,S△ABC=S△ADC,
∴S△ABC﹣S△AEP﹣S△PNC=S△ADC﹣S△AMP﹣S△PFC,
即四边形BEPN与四边形DMPF的面积相等;
故②正确;
∵PE=AM=c,
∴;
在△BPE中,BE+PE>PB,
即;
故③错误;
连接BD,
∵,;
在△PBD中,PB+PD≥BD,当点P位于对角线BD上时,等号成立;
∴;
故④不正确;
综上,正确的有2个;
故选:B.
二、填空题(共16分,每题2分)
9.(2分)函数y中,自变量x的取值范围是 x .
【解答】解:由题意得:2x﹣1≥0,
解得:x,
故答案为:x.
10.(2分)已知点A(2,y1)和点(3,y2)在直线y=﹣x+b上,则y1 > y2.(填>、<、=)
【解答】解:由条件可知y随x增大而减小,
∵点A(2,y1)和点(3,y2)在直线y=﹣x+b上,且2<3,
∴y1>y2,
故答案为:>.
11.(2分)下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差,根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择 乙 .
甲 乙 丙 丁
平均数(cm) 192 195 195 193
方差 3.2 4.7 6.5 6.0
【解答】解:根据题意可知:从平均数角度看应该从乙、丙中选择一人参赛,
从方差来看,应该选择乙参赛,
故答案为:乙.
12.(2分)某班级课堂从“理解”、“归纳”、“运用”、“综合”、“参与”等五方面按2:1:2:2:3的比例对学生学习过程进行课堂评价.某同学在课堂上五个方面得分如图所示,则该学生的课堂评价成绩为 8.1 .
【解答】解:根据加权平均数的计算方法可得:
,
故答案为:8.1.
13.(2分)如图,在矩形ABCD中,AD=12,AB=10,点Q是AB中点,点P为BC上任意一点,E、F分别是PQ、PD的中点,则EF的长是 .
【解答】解:连接DQ,
∵四边形ABCD是矩形,
∴∠A=90°,
∵Q是AB的中点,AB=10,AD=12,
∴,
∴,
∵E、F分别是PQ、PD的中点,
∴EF为△PDQ的中位线,
∴,
故答案为:.
14.(2分)如图,在平面直角坐标系xOy中,点A的坐标是,以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,则点B的坐标为 .
【解答】解:∵以AO为边作菱形OABC,若点C在x轴上,点B在第二象限,
∴只有一种情况,如图所示:
延长BA交y轴于点E,
∴BE⊥y轴,
∵点A的坐标是,
∴,
∴,
∴AO=AB=2,
∴BE=3,
∵点B在第二象限,
∴,
故答案为:.
15.(2分)如图,在矩形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,在平面直角坐标系xOy中,折线OEFG表示y与x之间的函数关系,当△APQ的面积是3时,x的值为 2或7 .
【解答】解:由函数图象可得,AB=4,S△ABP=6,
∵四边形ABCD是矩形,
∴AB=CD=4,∠ABC=90°,
∴,
∴BC=3;
由条件可知;
当点Q在AB上,且y的值为3时,则,解得x=2;
当点Q在BC上,且y的值为3时,则,解得x=7;
当点Q在CD上,且y的值为3时,则,解得x=7;
综上所述,x的值为2或7,
故答案为:2或7.
16.(2分)如图,已知AB=AC=3,∠BAC=90°,直线l是过点A的一条动直线(不与直线AB,AC重合),分别过点B,C作直线l的垂线,垂足为D,E.在直线l运动的过程中,DE的最大值为 .
【解答】解:∵∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵过点B,C作直线的垂线,垂足为D,E,
∴∠BDA=∠CEA=90°,
∴∠BAD+∠B=90°,
∴∠CAE=∠B,
∵AB=AC=3,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE,如图,
当直线l在∠BAC 内部时,D1E1=AD1﹣AE1,
当直线l在∠BAC外部时,D2E2=AD2+AE2,
∴DE 的值最大时,直线l在∠BAC 外部,
设AD2=CE2=x,BD2=AE2=y,
∴D2E2=AD2+AE2=x+y,
∵AB=AC=3,
∴x2+y2=32=9,
∵(x﹣y)2≥0,
∴x2+y2﹣2xy≥0,即2xy≤9,
∴(x+y)2=x2+y2+2xy=9+2xy≤18,
∵BD+AD>AB,
∴,
∴DE的最大值为,
故答案为:.
三、解答题(共68分,其中第17-22题每题5分,第23-26题每题6分,第27-28题每题7分)
17.(5分)计算:.
【解答】解:原式
.
18.(5分)计算:.
【解答】解:原式=3
=6
=5.
19.(5分)已知,如图,菱形ABCD的对角线AC,BD交于点O,
求作:矩形AOBE.
作法:①作AB的垂直平分线交AB于点F;
②连接OF并延长,在OF的延长线上截取点E,使EF=OF;
③连接AE,BE.
四边形AOBE为所求作的矩形.
(1)按要求利用直尺和圆规补全图形(保留作图痕迹);
(2)完成以下证明:
证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形.( 对角线互相平分的四边形为平行四边形 )(填推理依据)
∵四边形ABCD是菱形,
∴AC⊥BD,( 菱形的对角线互相垂直平分 )(填推理依据)
∴∠AOB=90°,
∴ AOBE是矩形.( 有一个内角为90°的平行四边形为矩形 )(填推理依据)
【解答】(1)解:如图,四边形AOBE为所;
(2)证明:∵AB的垂直平分线交AB于点F,
∴AF=BF.
∵BF=OF,
∴四边形AOBE是平行四边形(对角线互相平分的四边形为平行四边形),
∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直平分),
∴∠AOB=90°,
∴ AOBE是矩形(有一个内角为90°的平行四边形为矩形).
故答案为:对角线互相平分的四边形为平行四边形,菱形的对角线互相垂直平分,有一个内角为90°的平行四边形为矩形.
20.(5分)如图,小明家有一块三角形土地用来种植菠菜,其中AB=15m,AC=20m,BC=25m,小明想以B为起点挖一条水渠BD,点D在AC边上.水渠能将土地△ABC分成面积相等的两部分.分别用来种植两种不同蔬菜,又能同时对两种蔬菜进行灌溉.请帮小明计算一下水渠BD的准确长度.
【解答】解:∵AB=15m,AC=20m,BC=25m,
∴AB2+AC2=152+202=225+400=625,BC2=252=625,
∴AB2+AC2=BC2,
∴三角形ABC是直角三角形,∠A=90°,
∵BD平分△ABC的面积,
∴BD是△ABC中线,
∴ADAC=10m,
在直角三角形ABD中,由勾股定理得:BD5(m),
答:水渠BD的准确长度为m.
21.(5分)如图,在 ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,求证:BM=DN.
【解答】证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AB=CD,
∴∠BAM=∠DCN,
又在△ABM和△CDN中,
,
∴△ABM≌△CDN(SAS),
∴BM=DN.
22.(5分)共享电动车方便出行,是一种新理念下的交通工具.某天早上王老师想骑共享电动车去学校,有A,B两种品牌的共享电动车可选择.A,B两种品种共享电动车所收费用y(元)与骑行时间x(min)之间的函数图象如图所示.
(1)A品牌的共享电动车每分钟收费 0.4 元;骑行时间不超过10分钟时,B品牌的共享电动车一律收费 6 元.
(2)已知王老师家与学校的距离为4.5km,且王老师骑电动车的平均速度为300m/min,那么王老师选择哪种品牌的共享电动车会更省钱?求出此时使用两种品牌的共享电动车的价格差.
【解答】解:(1)根据图象得:8÷20=0.4元,
骑行时间不超过10分钟时,B品牌的共享电动车一律收费6元,
故答案为:0.4;6;
(2)选择B品牌共享电动车会更省钱.理由如下:
王老师从家骑行到学校所需时间为,
观察函数图象可知,当x=15时,yA<yB,
所以选择A品牌共享电动车会更省钱,
设yA=kx,将点(20,8)代入得:8=20k,
解得:k=0.4,
∴yA=0.4x,
设yB=mx+n,由条件可得:,
解得:,
∴yB=0.2x+4,
当x=15时,yA=6,yB=7,
yB﹣yA=1元.
23.(6分)如图,在△ABC中,AB=BC,过A点作BC的平行线与∠ABC的平分线交于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)连接AC与BD交于点O,过点D作DE⊥BC交BC的延长线于E点,连接EO,若EO,BE=4,求CE的长.
【解答】(1)证明:∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵AD∥BC,
∴∠ADB=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠ADB,
∴AB=AD,
∵AB=BC,
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BC,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴BO=DO,BC=CD,
∵DE⊥BC,
∴∠BED=90°,
∴,
∴,
设CE=x,则BC=CD=BE﹣CE=4﹣x,
在Rt△CDE中,由勾股定理得CD2=CE2+DE2,
∴(4﹣x)2=x2+22,
解得:,
∴CE的长为.
24.(6分)在平面直角坐标系xOy中.一次函数y=kx+b的图象平行于,且经过点A(4,1).
(1)求一次函数解析式;
(2)点P为x轴上一点,一次函数y=kx+b的图象与x轴交于点B,△ABP的面积是2,求点P坐标;
(3)当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,直接写出m的取值范围.
【解答】解:(1)∵一次函数y=kx+b的图象平行于直线y,
∴k,
把A(4,1)代入yx+b得,b=﹣1,
∴一次函数的表达式为:yx﹣1;
(2)令yx﹣1中y=0,则x=2,
∴B(2,0),
设点P的坐标为(n,0),则BP=|n﹣2|,
∵△ABP的面积是2,
∴BP yA2,
解得:n=6或n=﹣2,
∴点P坐标为(6,0)或(﹣2,0).
(3)如图:
,
把x=1代入y,求得y,
把(1,)代入y=m(x+1)(m≠0)得,2m,
解得m,
∵当x<1时,对于x的每一个值,函数y=m(x+1)(m≠0)的值均大于一次函数y=kx+b的值,
∴m的取值范围是m且m≠0.
25.(6分)百度推出了“文心一言”AI聊天机器人(以下简称甲款),抖音推出了“豆包”AI聊天机器人(以下简称乙款).有关人员开展了对甲,乙两数聊天机器人的使用满意度评分测验,并分别随机抽取20份评分数据.对数据进行整理、描述和分析(评分分数用x表示,分为四个等级:A:60<x≤70,B:70<x≤80,C:80<x≤90,D:90<x≤100).
下面给出了部分信息:
甲款评分数据中的数据:64,70,75,76,78,78,80,82,84,85,85.85,90,90,94,95,98,98,99,100.
乙款评分数据中C组包含的所有数据:87,88,84,87,89,87,81,90.
甲、乙款评分统计表:
设备 平均数 中位数 众败
甲 86 85 a
乙 86
根据以上信息,解答下列问题:
(1)上述图表中a= 85 ,b= 85.5 .m= 20 .
(2)在此次测验中,有200人对甲款进行评分,220人对乙款进行评分.请通过计算,估计其中对甲、乙两款聊天机器人非常满意(90<x≤100)的用户总人数是多少?
(3)如果让你选择一款AI聊天机器人,你会选择哪一款?请利用数据说明理由.
【解答】解:(1)甲款评分数据中,85分出现次数最多,则a=85,
A组B组共有20×(10%+30%)=8人,
将C组包含的所有数据排序为:81,84,87,87,87,88,89,90,
第十个和第十一个评分分别为84、87,
所以中位数.
乙款聊天机器人中,C组包含8个数据,所占比例为,
∴m%=1﹣40%﹣10%﹣30%=20%,
∴m=20,
故答案为:85,85.5;20;
(2)D组有20×20%=4人,
甲数据中D组有6人,
∴非常满意用户总人数人.
(3)甲乙款平均数都相同,但是乙的中位数85.5,甲的中位数85,
∴选择乙款聊天机器人.
26.(6分)请同学们探究函数y=2|x+1|﹣3的图象,通过列表、描点、画图,观察图象,并利用函数性质解决问题.
(1)画出函数y=2|x+1|﹣3的图象.
①列表:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 1 3 …
请补全表格:
②根据表格的数据,请在平面直角坐标系中描出对应点并连线,画出该函数图象.
(2)利用函数y=2|x+1|﹣3的图象,探索函数性质并解决问题:
①写出该函数的一条性质 函数图象关于x=﹣1对称(答案不唯一) ;
②当﹣2<x<2时,y的取值范围是 ﹣3≤y<3 ;
③若点M(x1,y1)与N(x2,y2)是函数y=2|x+1|﹣3图象上的两个点,若对于﹣3≤x1≤0,a≤x2≤a+1,都有y1<y2,则a的取值范围是 a>1或a<﹣4 .
【解答】解:(1)①当x=﹣2时,y=2×|﹣2+1|﹣3=﹣1,
当x=﹣1时,y=2×|﹣1+1|﹣3=﹣3,
补全表格如下:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 …
y … 3 1 ﹣1 ﹣3 ﹣1 1 3 …
②函数图象如图所示:
(2)①函数图象关于x=﹣1对称(答案不唯一),
故答案为:函数图象关于x=﹣1对称;
②由函数图象得,当﹣2<x<2时,﹣3≤y<3,
故答案为:﹣3≤y<3;
③∵﹣3≤x1≤0,
∴﹣3≤y1≤1,
结合图象得:a>1或a<﹣4,
故答案为:a>1或a<﹣4.
27.(7分)如图,在正方形ABCD中,E为BC上一点(不与BC重合),过点C作CF⊥AE交AE延长线于点F,连接BF,作DG⊥FC交FC的延长线于点G.
(1)补全图形并用等式表示线段AF,CF,AD的数量关系并证明:
(2)用等式表示线段BF与CG的数量关系并证明.
【解答】(1)解:补全图形如下:
连接AC,
∵四边形ABCD是正方形,
∴AD=CD,
∵CF⊥AE,
∴AF2+CF2=AC2=2AD2,
∴AF2+CF2=2AD2;
(2)过点B作BH⊥AF于点H,过点B作BM⊥CF于点M,如图所示:
∴∠AHB=∠BMC=90°,
∴∠ABH+∠CBH=90°,
∵CF⊥AE,
∴四边形BMFH为矩形,
∴∠HBM=90°,
∴∠ABH=∠MBC,
∵四边形ABCD是正方形,
∴AB=BC,
∴△ABH≌△CBM(AAS),
同理得:△DCG≌△CBM(AAS),
∴△ABH≌△CBM≌△DCG,
∴BH=CG=BM,
∴四边形BMFH为正方形,
∴.
同课章节目录
