2026年中考数学复习课件 专题一 选择题解题方法(共43张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题一 选择题解题方法(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 08:01:44 | ||
图片预览









文档简介
(共43张PPT)
复习讲义
第二篇 专题突破
专题一 选择题解题方法
方法一 直接法
根据选择题的已知条件,运用所学的各类公式、定理、定义等,
通过计算或推理直接求得结论,再与选项对照来确定正确的答案.这种
方法叫作直接法.
典题精析
例1 (2025·怀化·中考改编)不透明袋子中装有白球2个,红球1个,这
些球除颜色外无其他差别.从袋子中随机取出1个球,取出红球的概率是
( ).
A.1 B. C. D.
提示:将,代入,得(取出红球) .
B
思路点拨 直接运用概率公式 计算.
针对训练
1.(2024·广西·中考)激光测距仪发出的激光束以 的速度
射向目标,后测距仪收到反射回的激光束.则到的距离 与
时间 的关系式为( ).
A
A. B.
C. D.
提示:激光由到所用的时间为,速度为,则与 的
距离 .
方法二 观察法
有些选择题,通过观察函数图象或几何图形的特征,代数式、方
程或函数解析式的结构特点,结合相关数学知识可直接得出结论.这种
方法叫作观察法.
思路点拨 对于关于的一元二次方程,当,
异号时,的值一定大于0.因此对于方程 ,若
, 异号,则可确定这个方程有两个不相等的实数根.
典题精析
例2 (2025·四川自贡·中考模拟)对于关于 的一元一次方程
根的情况是( ).
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
提示:对于方程,,,即, 异号,则
的值一定大于0.故这个方程有两个不相等的实数根.
A
针对训练
图1
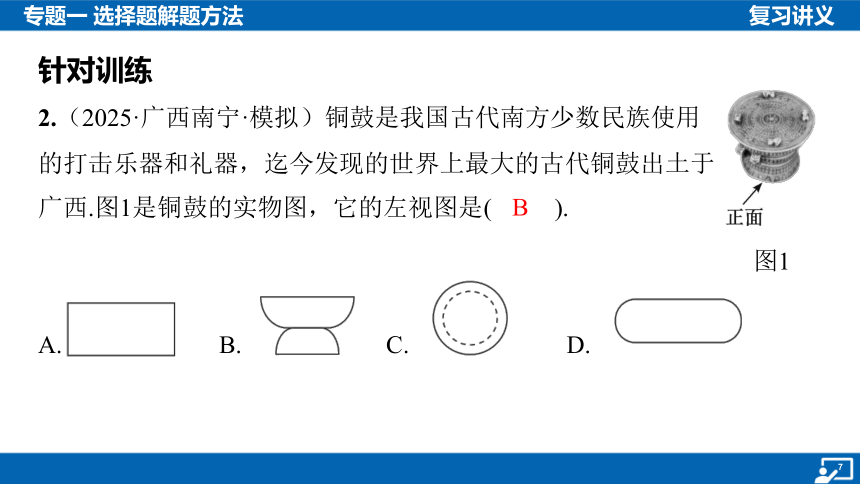
2.(2025·广西南宁·模拟)铜鼓是我国古代南方少数民族使用
的打击乐器和礼器,迄今发现的世界上最大的古代铜鼓出土于
广西.图1是铜鼓的实物图,它的左视图是( ).
B
A. B. C. D.
图2
3.(2025·广东广州·模拟)函数 与
的图象如图2所示,当,均随着 的增大而减
小时, 的取值范围是( ).
D
A. B.
C. D.
方法三 排除法
根据单项选择题有且只有一个正确选项的特征,我们可以考虑从
选项入手,根据题设条件与各选项的关系,通过分析、推理、计算、
判断,对所给选项进行筛选,将其中与题设相矛盾的选项逐一排除,
从而获得正确结论.这种方法叫作排除法,也叫淘汰法或筛选法.
典题精析
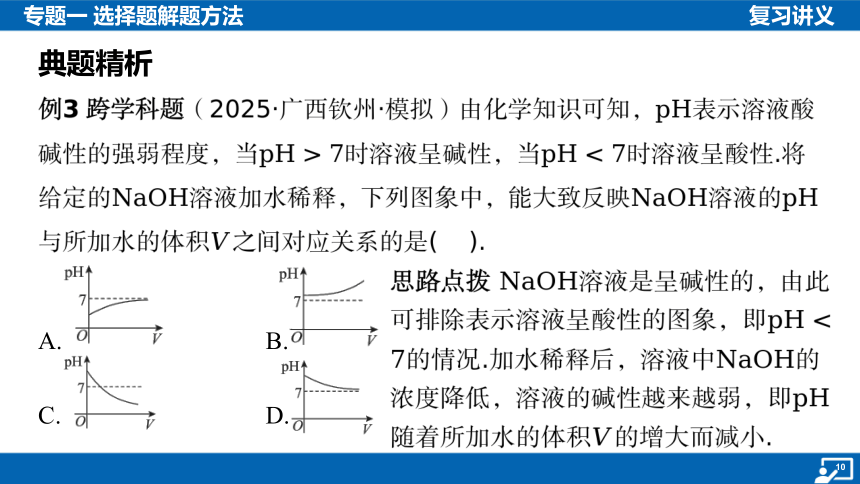
例3 跨学科题(2025·广西钦州·模拟)由化学知识可知, 表示溶液酸
碱性的强弱程度,当时溶液呈碱性,当 时溶液呈酸性.将
给定的溶液加水稀释,下列图象中,能大致反映溶液的
与所加水的体积 之间对应关系的是( ).
A. B.
C. D.
思路点拨 溶液是呈碱性的,由此可排除表示溶液呈酸性的图象,即的情况.加水稀释后,溶液中 的浓度降低,溶液的碱性越来越弱,即随着所加水的体积 的增大而减小.
提示:因为 溶液是呈碱性的,所以排除选项A,C.随着所加水的体积的增大,溶液的碱性越来越弱,故排除选项B,正确答案为选项D.
答案:D
针对训练
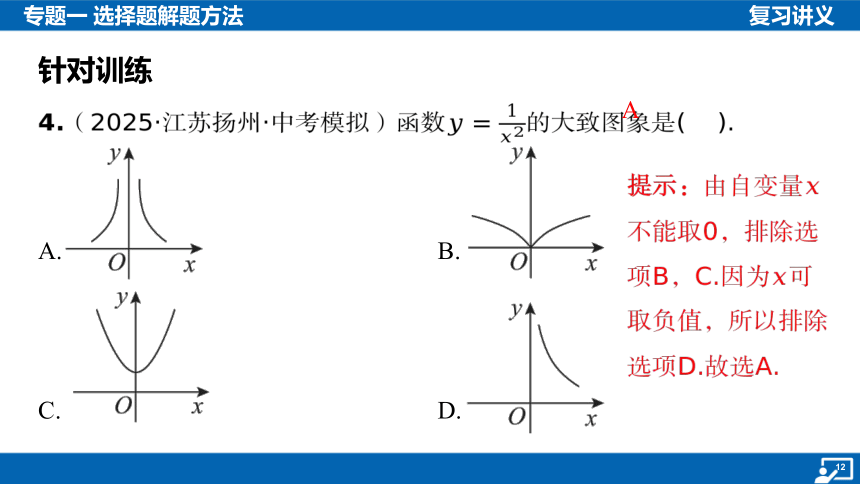
4.(2025·江苏扬州·中考模拟)函数 的大致图象是( ).
A. B.
C. D.
提示:由自变量不能取0,排除选项B,C.因为 可取负值,所以排除选项D.故选A.
A
方法四 特殊值法
特殊值法:根据题目中的条件,选取某个符合条件的特殊值或作
出特殊图形进行计算、推理的方法.当选择题的题设与字母的取值范围
有关时,我们可以赋予字母特殊值,利用特殊值排除错误答案.
选择特殊值时,要注意:(1)必须满足题目的所有条件,(2)
能使计算更简便.
典题精析
图3
例4 数学文化(2024·山东滨州·中考)刘徽是我国魏晋时
期伟大的数学家,中国古典数学理论的奠基者之一.刘徽
在注释《九章算术》时十分重视一题多解,其中最典型的
是勾股容方和勾股容圆公式的推导,他给出了内切圆直径
的多种表达形式.如图3,中, , ,
,的长分别为,,.可以用含,,的式子表示 的内切
圆直径 ,下列各式错误的是( ).
图3
A. B.
C. D.
提示: 令,, .选项A中, ;选项B中, ;选项C中, ;选项D中, .只有选项D与其他选项不一致,故选D.
【答案】D
图3
思路点拨 本题直接推理难度较大,可用特殊值法快速
得解.由是直角三角形,可令, ,
,代入各式计算出 的值,所得值与其他三个选
项不同的即为错误的式子.
针对训练
5.(2025·广西桂林·模拟)把因式分解得 ,
则 的值为( ).
B
A.2 B.4 C.6 D.8
提示:由题意,得.令 ,则
.解得 .
6.(2025·河北·中考)若为任意整数,则 的值总能
( ).
B
A.被2整除 B.被3整除 C.被5整除 D.被7整除
提示:由为任意整数,设,则 ,显然能被3整除.
方法五 数形结合法
数形结合是一种把数或数量关系与图形对应起来,借助图形来研
究数量关系或者利用数量关系来研究图形的性质的数学思想方法.它可
以使抽象的问题具体化,复杂的问题简单化.当选择题的题设与图形或
函数图象有关时,可以考虑用数形结合法解题.数形结合常与以下内容
有关:(1)实数与数轴上的点的对应关系,(2)函数与图象的对应
关系,(3)曲线(双曲线、抛物线)与方程、不等式的对应关系,等
等.
典题精析
例5 (2024·广西·中考)已知点,在反比例函数
的图象上,若 ,则有( ).
A. B. C. D.
提示:画出反比例函数的草图如图86所示.观察点, 的位置,可得 .
图86
A
思路点拨 画出反比例函数的草图,并标出和 的大致位置,观察图象即可比较, 与0的大小.
针对训练
图4
7.若二次函数 的部分图象如图4所示,则
关于的方程 的解为( ).
B
A., B.,
C., D.,
提示:由题图可知,抛物线的对称轴为直线 ,抛物线
与轴的一个交点坐标为,由此可得抛物线与 轴的另
一个交点坐标为,即当或3时,函数值 .
故关于的方程的解为, .
方法六 极端处理法
对于涉及动点的选择题,可以在满足题设条件的前提下,将动点
置于特殊位置或极端位置去思考,往往能快速得出正确答案,这种方
法称为极端处理法或极限法.
典题精析
图5
例6 (2025·广西桂林·模拟)如图5,已知函数
的图象与一次函数 的图象
有三个交点,则 的取值范围是( ).
A. B.
C. D.
思路点拨 画出一次函数 的极端图象如图6所示(图中的虚线),
再根据图象的特征求出 的取值范围.
图5
提示: 当时,函数,故 .
当一次函数的图象经过点A时, ,
解得.当一次函数的图象与 的
图象只有一个交点时, ,
,解得 .综上可
【答案】D
得,当时,函数 的图象与
一次函数 的图象有三个交点.
针对训练
图7
8.(2025·安徽·模拟)如图7,在矩形 中,对角线
,相交于点,,,点是边 上
一点,过点作于点,于点 ,则
的值是( ).
A.2.4 B.2.5 C.3 D.4
图87
提示:如图87,点是边上任意一点,不妨设点 与
点D重合,过点D作于点,此时 的
值即为线段 的长.由勾股定理,得
.由
【答案】A
,得 .所以
的值是2.4.
图8
9.如图8,矩形的边在轴上, 的中点
与原点重合,,.若过定点 和
动点的直线与矩形 的边有公共点,则
的取值范围是( ).
A. B.
C. D.
图88
提示:根据题意,得 ,
即,.如图88,当直线 过点D时,
点与点重合.设直线 对应的函数解析式为
,将代入,得 ,
即.故直线 对应的函数解析式为
.令,得,即 .当直线
过点C时,点与点重合,设直线 对应的
函数解析式为,将 代入,
得,即.故直线 对应的函
数解析式为.令,得 ,即
.结合图象可得,当过定点 和动点
的直线与矩形的边有公共点时, 的
取值范围是 .
【答案】D
图88
专题练习一 选择题解题方法
方法一 直接法
图1
1.(2024·江苏苏州·中考)如图1, ,若
, ,则 的度数为( ).
A.45 B. C. D.
提示:由, ,得
.所以
.
B
2.(2024·四川达州·中考)抛物线与 轴交于两点,其
中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正
确的是( ).
A
A. B. C. D.
提示:设抛物线与轴交于和 两点,且
,则,.由此可得 ,
即.由根与系数的关系可得, .所
以 .
方法二 观察法
3.(2024·广西·中考)端午节是我国传统节日,下列与端午节有关的文
创图案中,成轴对称的是( ).
B
A. B. C. D.
4.若,,则 的值为( ).
D
A.0 B.1 C.4 D.9
提示:观察代数式,发现各项有公因式 ,提取公
因式,得.因式分解,得 .
图2
5.(2025·湖北武汉·中考模拟)如图2,一个圆柱体水槽底部叠放
两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象
能大致反映水槽中水的深度与注水时间 的函数关系的是
( ).
D
A. B. C. D.
方法三 排除法
图3
6.(2024·黑龙江牡丹江·中考)如图3,在平面直角坐标系中,抛
物线与轴交于, 两点,
与轴的交点的纵坐标在到 之间.有以下结论:
A.①②④ B.①③④ C.①②③ D.①②③④
;;③若且 ,则
;④若直线与抛物线 的一
个交点的坐标为,则 . 其中正确的结论是( ).
图3
提示:每个选项都含有①,因此不需要验证①.由抛物线经
过, ,得
.所以 ,
.由点C的纵坐标在到 之间,得
.所以,即 .故②正确.由
【答案】A
此排除选项B.由,得 ,
即.从而得.又 ,
所以 .故③错误.由此排除选项C,D.故选A.
方法四 特殊值法
7.(2025·天津·中考模拟)计算 的结果等于( ).
C
A. B. C. D.
提示:令,则 .此时只有选项C的结果为1.
故选C.
8.(2025·呼和浩特·模拟)已知点,, 在同一
个函数图象上,则这个函数图象可能是( ).
A. B.
C. D.
提示:令,则,, .因此这个函数图象经过第四象限,与轴有2个交点.故排除选项B,C.点 在第四象限,且位于直线 的右侧,因此只有选项A符合题意.
A
方法五 数形结合法
9.(2025·广西百色·中考模拟)图4是利用割补法求图形面积的示意图,下列
公式中与之相对应的是( ).
A
图4
A. B.
C. D.
10.(2024·四川泸州·中考)已知二次函数
(是自变量)的图象只经过第一、二、四象限,则实数 的取值范围为
( ).
A. B. C. D.
提示:画出二次函数 的草图如图115.
图115
由此可得,故 .
【答案】A
方法六 极端处理法
图5
11.教材变式[人教版八下第63页实验与探究变式]如
图5,正方形的对角线,交于点,是
上的一点,连接,过点作交于点 .若
,则四边形 的面积为( ).
B
A. B.1 C.2 D.4
提示:取极端情形,设点与点B重合,则点 与点C重合,此种情形符
合题意,显然 .
图6
12.如图6,在平面直角坐标系中,直线 与双曲
线交于,两点,是以点 为圆心,1为
半径的圆上一动点,连接,为 的中点.若线段
长度的最大值为2,则 的值为( ).
A. B. C. D.
图6
提示:解:连接 .由反比例函数图象的对称性可
知,是的中点,则是 的中位线.所以
.当B,C,三点共线时,最大,则 最大,
而的最大值为2,故 的最大值为4.从而得
.设点B的坐标为 ,
【答案】A
则.所以.故 .
复习讲义
第二篇 专题突破
专题一 选择题解题方法
方法一 直接法
根据选择题的已知条件,运用所学的各类公式、定理、定义等,
通过计算或推理直接求得结论,再与选项对照来确定正确的答案.这种
方法叫作直接法.
典题精析
例1 (2025·怀化·中考改编)不透明袋子中装有白球2个,红球1个,这
些球除颜色外无其他差别.从袋子中随机取出1个球,取出红球的概率是
( ).
A.1 B. C. D.
提示:将,代入,得(取出红球) .
B
思路点拨 直接运用概率公式 计算.
针对训练
1.(2024·广西·中考)激光测距仪发出的激光束以 的速度
射向目标,后测距仪收到反射回的激光束.则到的距离 与
时间 的关系式为( ).
A
A. B.
C. D.
提示:激光由到所用的时间为,速度为,则与 的
距离 .
方法二 观察法
有些选择题,通过观察函数图象或几何图形的特征,代数式、方
程或函数解析式的结构特点,结合相关数学知识可直接得出结论.这种
方法叫作观察法.
思路点拨 对于关于的一元二次方程,当,
异号时,的值一定大于0.因此对于方程 ,若
, 异号,则可确定这个方程有两个不相等的实数根.
典题精析
例2 (2025·四川自贡·中考模拟)对于关于 的一元一次方程
根的情况是( ).
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
提示:对于方程,,,即, 异号,则
的值一定大于0.故这个方程有两个不相等的实数根.
A
针对训练
图1
2.(2025·广西南宁·模拟)铜鼓是我国古代南方少数民族使用
的打击乐器和礼器,迄今发现的世界上最大的古代铜鼓出土于
广西.图1是铜鼓的实物图,它的左视图是( ).
B
A. B. C. D.
图2
3.(2025·广东广州·模拟)函数 与
的图象如图2所示,当,均随着 的增大而减
小时, 的取值范围是( ).
D
A. B.
C. D.
方法三 排除法
根据单项选择题有且只有一个正确选项的特征,我们可以考虑从
选项入手,根据题设条件与各选项的关系,通过分析、推理、计算、
判断,对所给选项进行筛选,将其中与题设相矛盾的选项逐一排除,
从而获得正确结论.这种方法叫作排除法,也叫淘汰法或筛选法.
典题精析
例3 跨学科题(2025·广西钦州·模拟)由化学知识可知, 表示溶液酸
碱性的强弱程度,当时溶液呈碱性,当 时溶液呈酸性.将
给定的溶液加水稀释,下列图象中,能大致反映溶液的
与所加水的体积 之间对应关系的是( ).
A. B.
C. D.
思路点拨 溶液是呈碱性的,由此可排除表示溶液呈酸性的图象,即的情况.加水稀释后,溶液中 的浓度降低,溶液的碱性越来越弱,即随着所加水的体积 的增大而减小.
提示:因为 溶液是呈碱性的,所以排除选项A,C.随着所加水的体积的增大,溶液的碱性越来越弱,故排除选项B,正确答案为选项D.
答案:D
针对训练
4.(2025·江苏扬州·中考模拟)函数 的大致图象是( ).
A. B.
C. D.
提示:由自变量不能取0,排除选项B,C.因为 可取负值,所以排除选项D.故选A.
A
方法四 特殊值法
特殊值法:根据题目中的条件,选取某个符合条件的特殊值或作
出特殊图形进行计算、推理的方法.当选择题的题设与字母的取值范围
有关时,我们可以赋予字母特殊值,利用特殊值排除错误答案.
选择特殊值时,要注意:(1)必须满足题目的所有条件,(2)
能使计算更简便.
典题精析
图3
例4 数学文化(2024·山东滨州·中考)刘徽是我国魏晋时
期伟大的数学家,中国古典数学理论的奠基者之一.刘徽
在注释《九章算术》时十分重视一题多解,其中最典型的
是勾股容方和勾股容圆公式的推导,他给出了内切圆直径
的多种表达形式.如图3,中, , ,
,的长分别为,,.可以用含,,的式子表示 的内切
圆直径 ,下列各式错误的是( ).
图3
A. B.
C. D.
提示: 令,, .选项A中, ;选项B中, ;选项C中, ;选项D中, .只有选项D与其他选项不一致,故选D.
【答案】D
图3
思路点拨 本题直接推理难度较大,可用特殊值法快速
得解.由是直角三角形,可令, ,
,代入各式计算出 的值,所得值与其他三个选
项不同的即为错误的式子.
针对训练
5.(2025·广西桂林·模拟)把因式分解得 ,
则 的值为( ).
B
A.2 B.4 C.6 D.8
提示:由题意,得.令 ,则
.解得 .
6.(2025·河北·中考)若为任意整数,则 的值总能
( ).
B
A.被2整除 B.被3整除 C.被5整除 D.被7整除
提示:由为任意整数,设,则 ,显然能被3整除.
方法五 数形结合法
数形结合是一种把数或数量关系与图形对应起来,借助图形来研
究数量关系或者利用数量关系来研究图形的性质的数学思想方法.它可
以使抽象的问题具体化,复杂的问题简单化.当选择题的题设与图形或
函数图象有关时,可以考虑用数形结合法解题.数形结合常与以下内容
有关:(1)实数与数轴上的点的对应关系,(2)函数与图象的对应
关系,(3)曲线(双曲线、抛物线)与方程、不等式的对应关系,等
等.
典题精析
例5 (2024·广西·中考)已知点,在反比例函数
的图象上,若 ,则有( ).
A. B. C. D.
提示:画出反比例函数的草图如图86所示.观察点, 的位置,可得 .
图86
A
思路点拨 画出反比例函数的草图,并标出和 的大致位置,观察图象即可比较, 与0的大小.
针对训练
图4
7.若二次函数 的部分图象如图4所示,则
关于的方程 的解为( ).
B
A., B.,
C., D.,
提示:由题图可知,抛物线的对称轴为直线 ,抛物线
与轴的一个交点坐标为,由此可得抛物线与 轴的另
一个交点坐标为,即当或3时,函数值 .
故关于的方程的解为, .
方法六 极端处理法
对于涉及动点的选择题,可以在满足题设条件的前提下,将动点
置于特殊位置或极端位置去思考,往往能快速得出正确答案,这种方
法称为极端处理法或极限法.
典题精析
图5
例6 (2025·广西桂林·模拟)如图5,已知函数
的图象与一次函数 的图象
有三个交点,则 的取值范围是( ).
A. B.
C. D.
思路点拨 画出一次函数 的极端图象如图6所示(图中的虚线),
再根据图象的特征求出 的取值范围.
图5
提示: 当时,函数,故 .
当一次函数的图象经过点A时, ,
解得.当一次函数的图象与 的
图象只有一个交点时, ,
,解得 .综上可
【答案】D
得,当时,函数 的图象与
一次函数 的图象有三个交点.
针对训练
图7
8.(2025·安徽·模拟)如图7,在矩形 中,对角线
,相交于点,,,点是边 上
一点,过点作于点,于点 ,则
的值是( ).
A.2.4 B.2.5 C.3 D.4
图87
提示:如图87,点是边上任意一点,不妨设点 与
点D重合,过点D作于点,此时 的
值即为线段 的长.由勾股定理,得
.由
【答案】A
,得 .所以
的值是2.4.
图8
9.如图8,矩形的边在轴上, 的中点
与原点重合,,.若过定点 和
动点的直线与矩形 的边有公共点,则
的取值范围是( ).
A. B.
C. D.
图88
提示:根据题意,得 ,
即,.如图88,当直线 过点D时,
点与点重合.设直线 对应的函数解析式为
,将代入,得 ,
即.故直线 对应的函数解析式为
.令,得,即 .当直线
过点C时,点与点重合,设直线 对应的
函数解析式为,将 代入,
得,即.故直线 对应的函
数解析式为.令,得 ,即
.结合图象可得,当过定点 和动点
的直线与矩形的边有公共点时, 的
取值范围是 .
【答案】D
图88
专题练习一 选择题解题方法
方法一 直接法
图1
1.(2024·江苏苏州·中考)如图1, ,若
, ,则 的度数为( ).
A.45 B. C. D.
提示:由, ,得
.所以
.
B
2.(2024·四川达州·中考)抛物线与 轴交于两点,其
中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正
确的是( ).
A
A. B. C. D.
提示:设抛物线与轴交于和 两点,且
,则,.由此可得 ,
即.由根与系数的关系可得, .所
以 .
方法二 观察法
3.(2024·广西·中考)端午节是我国传统节日,下列与端午节有关的文
创图案中,成轴对称的是( ).
B
A. B. C. D.
4.若,,则 的值为( ).
D
A.0 B.1 C.4 D.9
提示:观察代数式,发现各项有公因式 ,提取公
因式,得.因式分解,得 .
图2
5.(2025·湖北武汉·中考模拟)如图2,一个圆柱体水槽底部叠放
两个底面半径不等的实心圆柱体,向水槽匀速注水.下列图象
能大致反映水槽中水的深度与注水时间 的函数关系的是
( ).
D
A. B. C. D.
方法三 排除法
图3
6.(2024·黑龙江牡丹江·中考)如图3,在平面直角坐标系中,抛
物线与轴交于, 两点,
与轴的交点的纵坐标在到 之间.有以下结论:
A.①②④ B.①③④ C.①②③ D.①②③④
;;③若且 ,则
;④若直线与抛物线 的一
个交点的坐标为,则 . 其中正确的结论是( ).
图3
提示:每个选项都含有①,因此不需要验证①.由抛物线经
过, ,得
.所以 ,
.由点C的纵坐标在到 之间,得
.所以,即 .故②正确.由
【答案】A
此排除选项B.由,得 ,
即.从而得.又 ,
所以 .故③错误.由此排除选项C,D.故选A.
方法四 特殊值法
7.(2025·天津·中考模拟)计算 的结果等于( ).
C
A. B. C. D.
提示:令,则 .此时只有选项C的结果为1.
故选C.
8.(2025·呼和浩特·模拟)已知点,, 在同一
个函数图象上,则这个函数图象可能是( ).
A. B.
C. D.
提示:令,则,, .因此这个函数图象经过第四象限,与轴有2个交点.故排除选项B,C.点 在第四象限,且位于直线 的右侧,因此只有选项A符合题意.
A
方法五 数形结合法
9.(2025·广西百色·中考模拟)图4是利用割补法求图形面积的示意图,下列
公式中与之相对应的是( ).
A
图4
A. B.
C. D.
10.(2024·四川泸州·中考)已知二次函数
(是自变量)的图象只经过第一、二、四象限,则实数 的取值范围为
( ).
A. B. C. D.
提示:画出二次函数 的草图如图115.
图115
由此可得,故 .
【答案】A
方法六 极端处理法
图5
11.教材变式[人教版八下第63页实验与探究变式]如
图5,正方形的对角线,交于点,是
上的一点,连接,过点作交于点 .若
,则四边形 的面积为( ).
B
A. B.1 C.2 D.4
提示:取极端情形,设点与点B重合,则点 与点C重合,此种情形符
合题意,显然 .
图6
12.如图6,在平面直角坐标系中,直线 与双曲
线交于,两点,是以点 为圆心,1为
半径的圆上一动点,连接,为 的中点.若线段
长度的最大值为2,则 的值为( ).
A. B. C. D.
图6
提示:解:连接 .由反比例函数图象的对称性可
知,是的中点,则是 的中位线.所以
.当B,C,三点共线时,最大,则 最大,
而的最大值为2,故 的最大值为4.从而得
.设点B的坐标为 ,
【答案】A
则.所以.故 .
同课章节目录
