阶段质量检测(三) 万有引力与宇宙航行(含解析)高中物理人教版(2019)必修 第二册
文档属性
| 名称 | 阶段质量检测(三) 万有引力与宇宙航行(含解析)高中物理人教版(2019)必修 第二册 |  | |
| 格式 | DOC | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-14 08:40:06 | ||
图片预览




文档简介
阶段质量检测(三) 万有引力与宇宙航行
(本试卷满分:100分)
一、单项选择题(本题共7小题,每小题4分,共28分。每小题只有一个选项符合题目要求)
1.关于天体运动,下列说法正确的是( )
A.在太阳系中,各行星都围绕太阳运动
B.在太阳系中,各行星都围绕地球运动
C.地心说的参考系是太阳
D.日心说的参考系是地球
2.若使两质点间的万有引力减小为原来的,下列办法可采用的是( )
A.使两质点间距离增为原来的4倍,质量不变
B.使两质点的质量都减半,间距减为原来的
C.使其中一质点的质量减为原来的,间距不变
D.使两质点的质量和间距都减为原来的
3.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动。由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G,由此可求出S2的质量为( )
A. B.
C. D.
4.2024年1月17日,搭载天舟七号货运飞船的长征七号遥八运载火箭成功发射,天舟七号携带物资进入距离地面约400 km(小于地球同步卫星与地面的距离)的轨道,顺利对接中国空间站后近似做匀速圆周运动。对接后,这批物资( )
A.质量比静止在地面上时小
B.所受合力比静止在地面上时小
C.所受地球引力比静止在地面上时大
D.做圆周运动的角速度大小比地球自转角速度大
5.我国在太原卫星发射中心使用长征二号丁运载火箭,以“一箭四星”的方式,成功将宏图一号01组卫星发射升空,本次任务的四颗卫星在轨组成国际首个车轮式卫星编队。假设某卫星在预定轨道上绕地球做匀速圆周运动,其线速度大小为v,角速度大小为ω,引力常量为G,则地球的质量为( )
A. B.
C. D.
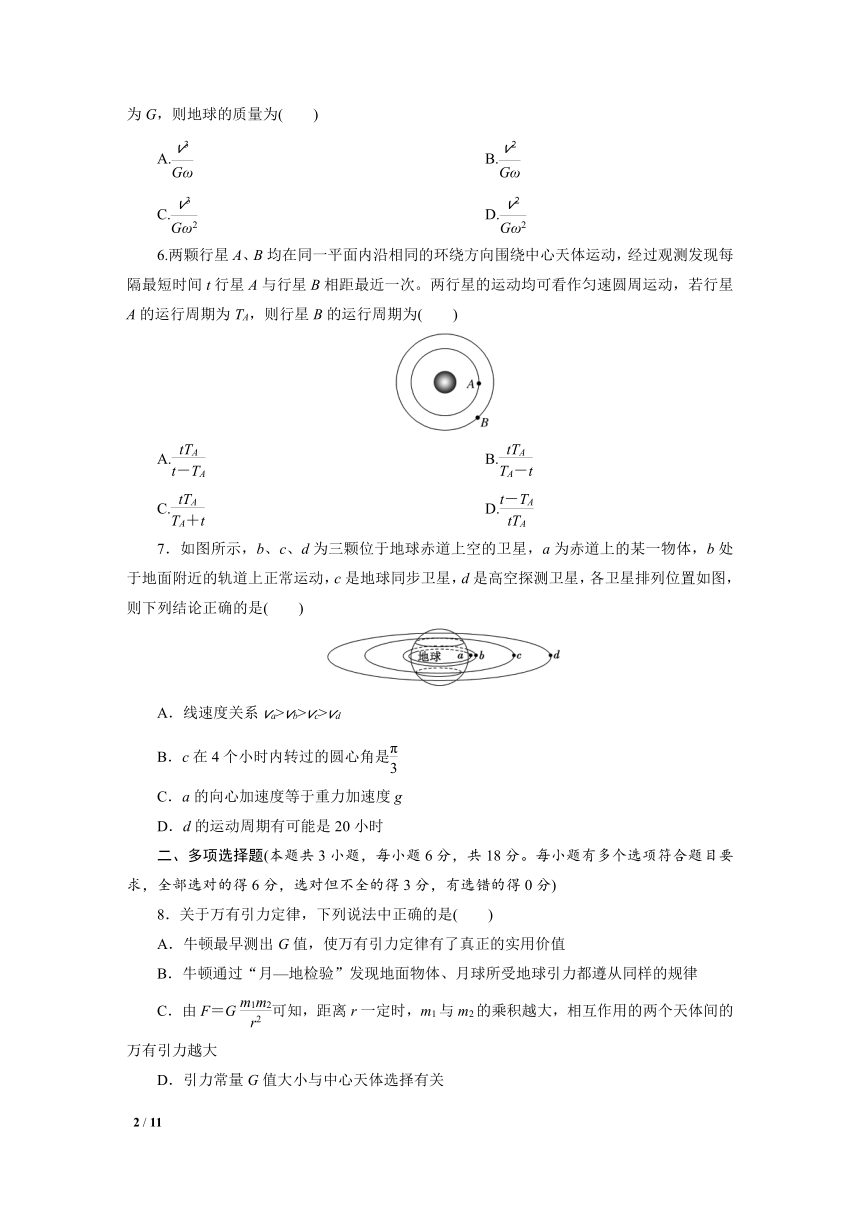
6.两颗行星A、B均在同一平面内沿相同的环绕方向围绕中心天体运动,经过观测发现每隔最短时间t行星A与行星B相距最近一次。两行星的运动均可看作匀速圆周运动,若行星A的运行周期为TA,则行星B的运行周期为( )
A. B.
C. D.
7.如图所示,b、c、d为三颗位于地球赤道上空的卫星,a为赤道上的某一物体,b处于地面附近的轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图,则下列结论正确的是( )
A.线速度关系va>vb>vc>vd
B.c在4个小时内转过的圆心角是
C.a的向心加速度等于重力加速度g
D.d的运动周期有可能是20小时
二、多项选择题(本题共3小题,每小题6分,共18分。每小题有多个选项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分)
8.关于万有引力定律,下列说法中正确的是( )
A.牛顿最早测出G值,使万有引力定律有了真正的实用价值
B.牛顿通过“月—地检验”发现地面物体、月球所受地球引力都遵从同样的规律
C.由F=G可知,距离r一定时,m1与m2的乘积越大,相互作用的两个天体间的万有引力越大
D.引力常量G值大小与中心天体选择有关
9.宇宙中存在一些离其他恒星较远的三星系统,在它们之间的万有引力作用下,绕一个共同的圆心做周期相等的圆周运动。如图所示,三颗质量均为m的星球构成三星系统Ⅰ,三颗质量均为km的星球构成三星系统Ⅱ,它们分别位于两个等边三角形的顶点上,若三星系统Ⅱ中等边三角形的边长是三星系统Ⅰ中等边三角形边长的q倍。下列说法正确的是( )
A.三星系统Ⅱ中一个星球受到的合力是三星系统Ⅰ中一个星球受到合力的倍
B.三星系统Ⅱ中一个星球的加速度是三星系统Ⅰ中一个星球加速度的倍
C.三星系统Ⅱ中一个星球的角速度是三星系统Ⅰ中一个星球角速度的 倍
D.三星系统Ⅱ中一个星球的线速度是三星系统Ⅰ中一个星球线速度的 倍
10.2024年4月25日20时59分,搭载神舟十八号载人飞船的长征二号F遥十八运载火箭在酒泉卫星发射中心点火发射。4月26日,神舟十八号载人飞船与空间站组合体完成自主快速交会对接。飞船的发射过程可简化为:飞船从预定轨道Ⅰ的A点第一次变轨进入椭圆轨道Ⅱ,到达椭圆轨道的远地点B时,再次变轨进入空间站的运行轨道Ⅲ,与空间站实现对接。假设轨道Ⅰ和Ⅲ都近似为圆轨道,不计飞船质量的变化,空间站轨道距地面的高度为h,地球半径为R,地球表面的重力加速度为g,下列说法正确的是( )
A.飞船在椭圆轨道Ⅱ经过A点的速度大于飞船在圆轨道Ⅰ经过A点的速度
B.飞船在椭圆轨道Ⅱ经过A点的速度一定大于7.9 km/s
C.飞船在椭圆轨道Ⅱ经过A点的加速度与飞船在圆轨道Ⅰ经过A点的加速度大小相等
D.飞船沿轨道Ⅱ由A点到B点的时间为
三、非选择题(本题共4小题,共54分)
11.(10分)太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到火星和太阳之间,且三者几乎排成一条直线的时候,天文学称为“火星冲日”。已知火星公转半径与地球公转半径的比值为C(C为常数),地球的公转周期为T,求:
(1)火星公转周期T火;
(2)相邻两次火星冲日的时间间隔Δt。
12.(12分)石墨烯是一种具有超轻超高强度的新型材料。有人设想:用石墨烯制作超级缆绳连接地球赤道上的固定基地与同步空间站,利用超级缆绳承载太空电梯从地球基地向空间站运送物资。已知地球半径为R,自转周期为T,地球北极表面重力加速度为g0,引力常量为G。
(1)求地球的质量M;
(2)太空电梯停在距地3R的站点,求该站点处的重力加速度g的大小。
13.(14分)“玉兔号”月球车与月球表面的第一次接触实现了中国人“奔月”的伟大梦想。不久的将来我国航天员登上月球,在月球表面做了一个平抛试验,将一物体从高h处以初速度v0水平抛出,测得水平位移为x,已知月球半径为R,自转周期为T,引力常量为G。求:
(1)月球表面重力加速度;
(2)月球的质量和月球的第一宇宙速度;
(3)月球的平均密度。
14.(18分)已知地球半径为R,空间站距离地面高度为h,地球表面重力加速度为g,引力常量为G。
(1)求地球的平均密度;
(2)求空间站绕地球做匀速圆周运动的周期;
(3)若已知空间站距离地面的高度为h=,地球同步卫星距离地面的高度为空间站距地面高度的90倍,试计算空间站的运行周期约为多少小时。(已知地球自转周期为24小时,结果保留两位有效数字)
阶段质量检测(三)
1.选A 地心说认为太阳及其他天体围绕地球运动,日心说认为太阳是宇宙的中心;在太阳系中,各行星都围绕太阳运动。故选A。
2.选C 根据万有引力定律可知,质点间的万有引力大小为F=G,使两质点间距离增为原来的4倍,质量不变,则万有引力减小为原来的,故A错误;使两质点的质量都减半,间距减为原来的,则万有引力保持不变,故B错误;使其中一质点的质量减为原来的,间距不变,则万有引力减小为原来的,故C正确;使两质点的质量和间距都减为原来的,则万有引力保持不变,故D错误。
3.选D 对星体S1由万有引力提供向心力有G=m1r1,可得S2的质量为m2=,故选D。
4.选D 物资在低速(速度远小于光速)宏观条件下质量保持不变,即在空间站中和在地面上质量相同,故A错误;设空间站离地面的高度为h,这批物资在地面上静止时合力为零,在空间站所受合力为万有引力,即F=,在地面受地球引力为F1=,因此有F1>F,故B、C错误;物资在空间站内绕地球做匀速圆周运动,万有引力提供向心力有=mω2r,解得ω=,空间站的轨道半径小于地球同步卫星的轨道半径,即这批物资做圆周运动的角速度大小比地球自转的角速度大,故D正确。
5.选A 根据G=mω2r,v=ωr,解得M=,故选A。
6.选A 半径越小,周期越小,故TB>TA, 从第一次相距最近到第二次相距最近,A比B多走一周,θA-θB=2π=t-t,解得TB=,故选A。
7.选B a为赤道上的某一物体,c是地球同步卫星,则a、c的角速度相等,根据v=ωr可知,线速度关系va8.选BC 最早测出G值的是卡文迪什,故A错误;牛顿通过“月—地检验”发现地面物体、月球所受地球引力都遵从同样的规律,故B正确;由公式F=G可知,G为引力常量,r一定时,m1与m2的乘积越大,F越大,故C正确;引力常量G是一个定值,它的大小与中心天体选择无关,故D错误。
9.选AD 设三星系统Ⅰ中等边三角形的边长为L,则三星系统Ⅱ中等边三角形的边长为qL,根据万有引力提供向心力可得 =ma=m=mω2×, =kma′=km=kmω′2×,所以系统Ⅱ中一个星球受到的合力是系统Ⅰ中一个星球受到的合力的=倍,系统Ⅱ中一个星球的加速度是系统Ⅰ中一个星球的加速度的==倍,系统Ⅱ中一个星球的角速度是系统Ⅰ中一个星球的角速度的==倍,系统Ⅱ中一个星球的线速度是系统Ⅰ中一个星球的线速度的== 倍,故选A、D。
10.选AC 根据变轨原理,飞船在圆轨道Ⅰ的A点需加速做离心运动进入椭圆轨道Ⅱ,故飞船在椭圆轨道Ⅱ经过A点的速度大于飞船在圆轨道Ⅰ经过A点的速度,故A正确;第一宇宙速度为7.9 km/s,是最大环绕速度,故飞船在椭圆轨道Ⅱ经过A点的速度一定小于7.9 km/s,故B错误;根据牛顿第二定律有G=ma,故飞船在椭圆轨道Ⅱ经过A点的加速度与飞船在圆轨道Ⅰ经过A点的加速度大小相等,故C正确;根据万有引力与重力的关系G=mg,根据万有引力提供向心力有G=m(R+h),解得飞船在轨道Ⅲ的周期为T=,根据开普勒第三定律=k,由轨道Ⅱ的半长轴小于轨道Ⅲ的半径,可知飞船在轨道Ⅱ的周期TⅡ小于轨道Ⅲ的周期T,飞船沿轨道Ⅱ由A点到B点的时间为t=TⅡ11.解析:(1)由开普勒第三定律得=
解得T火=CT。
(2)由题意得ω地Δt=ω火Δt+2π
由角速度和周期关系得Δt=Δt+2π
解得Δt=。
答案:(1)CT (2)
12.解析:(1)设质量为m0的物体在北极地面静止,则m0g0=G,解得M=。
(2)设货物质量为m,在距地面高3R站点受到的万有引力为F,则F=G,货物绕地球做匀速圆周运动,设太空电梯对货物的支持力为N,则F-N=mω2·4R
N=mg
ω=
联立解得g=-。
答案:(1) (2)-
13.解析:(1)设月球表面重力加速度为g,由平抛运动规律有
h=gt2,x=v0t
解得g=。
(2)在月球表面的物体受到的重力等于万有引力mg=G
解得M=
月球的第一宇宙速度为近月卫星的运行速度,根据重力提供向心力有mg=m
解得v1== 。
(3)月球的平均密度ρ===。
答案:(1) (2) (3)
14.解析:(1)地球表面一质量为m的物体,其受到的万有引力等于重力,所以有=mg
解得地球质量为M=
则地球的平均密度为ρ===。
(2)空间站绕地球做匀速圆周运动,由万有引力提供向心力,所以有=m·(R+h)
解得周期为T=2π。
(3)设空间站与同步卫星的轨道半径分别为r1和r2,运行周期分别为T1和T2,由开普勒第三定律可得=
则根据题意可知,空间站与同步卫星的轨道半径分别为
r1=R+=R=17h
r2=R+×90=R=106h
可以得到空间站的周期为
T1== h≈1.5 h。
答案:(1) (2)2π (3)1.5小时
7 / 7
(本试卷满分:100分)
一、单项选择题(本题共7小题,每小题4分,共28分。每小题只有一个选项符合题目要求)
1.关于天体运动,下列说法正确的是( )
A.在太阳系中,各行星都围绕太阳运动
B.在太阳系中,各行星都围绕地球运动
C.地心说的参考系是太阳
D.日心说的参考系是地球
2.若使两质点间的万有引力减小为原来的,下列办法可采用的是( )
A.使两质点间距离增为原来的4倍,质量不变
B.使两质点的质量都减半,间距减为原来的
C.使其中一质点的质量减为原来的,间距不变
D.使两质点的质量和间距都减为原来的
3.某双星由质量不等的星体S1和S2构成,两星在相互之间的万有引力作用下绕两者连线上某一定点C做匀速圆周运动。由天文观察测得其运动周期为T,S1到C点的距离为r1,S1和S2的距离为r,已知引力常量为G,由此可求出S2的质量为( )
A. B.
C. D.
4.2024年1月17日,搭载天舟七号货运飞船的长征七号遥八运载火箭成功发射,天舟七号携带物资进入距离地面约400 km(小于地球同步卫星与地面的距离)的轨道,顺利对接中国空间站后近似做匀速圆周运动。对接后,这批物资( )
A.质量比静止在地面上时小
B.所受合力比静止在地面上时小
C.所受地球引力比静止在地面上时大
D.做圆周运动的角速度大小比地球自转角速度大
5.我国在太原卫星发射中心使用长征二号丁运载火箭,以“一箭四星”的方式,成功将宏图一号01组卫星发射升空,本次任务的四颗卫星在轨组成国际首个车轮式卫星编队。假设某卫星在预定轨道上绕地球做匀速圆周运动,其线速度大小为v,角速度大小为ω,引力常量为G,则地球的质量为( )
A. B.
C. D.
6.两颗行星A、B均在同一平面内沿相同的环绕方向围绕中心天体运动,经过观测发现每隔最短时间t行星A与行星B相距最近一次。两行星的运动均可看作匀速圆周运动,若行星A的运行周期为TA,则行星B的运行周期为( )
A. B.
C. D.
7.如图所示,b、c、d为三颗位于地球赤道上空的卫星,a为赤道上的某一物体,b处于地面附近的轨道上正常运动,c是地球同步卫星,d是高空探测卫星,各卫星排列位置如图,则下列结论正确的是( )
A.线速度关系va>vb>vc>vd
B.c在4个小时内转过的圆心角是
C.a的向心加速度等于重力加速度g
D.d的运动周期有可能是20小时
二、多项选择题(本题共3小题,每小题6分,共18分。每小题有多个选项符合题目要求,全部选对的得6分,选对但不全的得3分,有选错的得0分)
8.关于万有引力定律,下列说法中正确的是( )
A.牛顿最早测出G值,使万有引力定律有了真正的实用价值
B.牛顿通过“月—地检验”发现地面物体、月球所受地球引力都遵从同样的规律
C.由F=G可知,距离r一定时,m1与m2的乘积越大,相互作用的两个天体间的万有引力越大
D.引力常量G值大小与中心天体选择有关
9.宇宙中存在一些离其他恒星较远的三星系统,在它们之间的万有引力作用下,绕一个共同的圆心做周期相等的圆周运动。如图所示,三颗质量均为m的星球构成三星系统Ⅰ,三颗质量均为km的星球构成三星系统Ⅱ,它们分别位于两个等边三角形的顶点上,若三星系统Ⅱ中等边三角形的边长是三星系统Ⅰ中等边三角形边长的q倍。下列说法正确的是( )
A.三星系统Ⅱ中一个星球受到的合力是三星系统Ⅰ中一个星球受到合力的倍
B.三星系统Ⅱ中一个星球的加速度是三星系统Ⅰ中一个星球加速度的倍
C.三星系统Ⅱ中一个星球的角速度是三星系统Ⅰ中一个星球角速度的 倍
D.三星系统Ⅱ中一个星球的线速度是三星系统Ⅰ中一个星球线速度的 倍
10.2024年4月25日20时59分,搭载神舟十八号载人飞船的长征二号F遥十八运载火箭在酒泉卫星发射中心点火发射。4月26日,神舟十八号载人飞船与空间站组合体完成自主快速交会对接。飞船的发射过程可简化为:飞船从预定轨道Ⅰ的A点第一次变轨进入椭圆轨道Ⅱ,到达椭圆轨道的远地点B时,再次变轨进入空间站的运行轨道Ⅲ,与空间站实现对接。假设轨道Ⅰ和Ⅲ都近似为圆轨道,不计飞船质量的变化,空间站轨道距地面的高度为h,地球半径为R,地球表面的重力加速度为g,下列说法正确的是( )
A.飞船在椭圆轨道Ⅱ经过A点的速度大于飞船在圆轨道Ⅰ经过A点的速度
B.飞船在椭圆轨道Ⅱ经过A点的速度一定大于7.9 km/s
C.飞船在椭圆轨道Ⅱ经过A点的加速度与飞船在圆轨道Ⅰ经过A点的加速度大小相等
D.飞船沿轨道Ⅱ由A点到B点的时间为
三、非选择题(本题共4小题,共54分)
11.(10分)太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动。当地球恰好运行到火星和太阳之间,且三者几乎排成一条直线的时候,天文学称为“火星冲日”。已知火星公转半径与地球公转半径的比值为C(C为常数),地球的公转周期为T,求:
(1)火星公转周期T火;
(2)相邻两次火星冲日的时间间隔Δt。
12.(12分)石墨烯是一种具有超轻超高强度的新型材料。有人设想:用石墨烯制作超级缆绳连接地球赤道上的固定基地与同步空间站,利用超级缆绳承载太空电梯从地球基地向空间站运送物资。已知地球半径为R,自转周期为T,地球北极表面重力加速度为g0,引力常量为G。
(1)求地球的质量M;
(2)太空电梯停在距地3R的站点,求该站点处的重力加速度g的大小。
13.(14分)“玉兔号”月球车与月球表面的第一次接触实现了中国人“奔月”的伟大梦想。不久的将来我国航天员登上月球,在月球表面做了一个平抛试验,将一物体从高h处以初速度v0水平抛出,测得水平位移为x,已知月球半径为R,自转周期为T,引力常量为G。求:
(1)月球表面重力加速度;
(2)月球的质量和月球的第一宇宙速度;
(3)月球的平均密度。
14.(18分)已知地球半径为R,空间站距离地面高度为h,地球表面重力加速度为g,引力常量为G。
(1)求地球的平均密度;
(2)求空间站绕地球做匀速圆周运动的周期;
(3)若已知空间站距离地面的高度为h=,地球同步卫星距离地面的高度为空间站距地面高度的90倍,试计算空间站的运行周期约为多少小时。(已知地球自转周期为24小时,结果保留两位有效数字)
阶段质量检测(三)
1.选A 地心说认为太阳及其他天体围绕地球运动,日心说认为太阳是宇宙的中心;在太阳系中,各行星都围绕太阳运动。故选A。
2.选C 根据万有引力定律可知,质点间的万有引力大小为F=G,使两质点间距离增为原来的4倍,质量不变,则万有引力减小为原来的,故A错误;使两质点的质量都减半,间距减为原来的,则万有引力保持不变,故B错误;使其中一质点的质量减为原来的,间距不变,则万有引力减小为原来的,故C正确;使两质点的质量和间距都减为原来的,则万有引力保持不变,故D错误。
3.选D 对星体S1由万有引力提供向心力有G=m1r1,可得S2的质量为m2=,故选D。
4.选D 物资在低速(速度远小于光速)宏观条件下质量保持不变,即在空间站中和在地面上质量相同,故A错误;设空间站离地面的高度为h,这批物资在地面上静止时合力为零,在空间站所受合力为万有引力,即F=,在地面受地球引力为F1=,因此有F1>F,故B、C错误;物资在空间站内绕地球做匀速圆周运动,万有引力提供向心力有=mω2r,解得ω=,空间站的轨道半径小于地球同步卫星的轨道半径,即这批物资做圆周运动的角速度大小比地球自转的角速度大,故D正确。
5.选A 根据G=mω2r,v=ωr,解得M=,故选A。
6.选A 半径越小,周期越小,故TB>TA, 从第一次相距最近到第二次相距最近,A比B多走一周,θA-θB=2π=t-t,解得TB=,故选A。
7.选B a为赤道上的某一物体,c是地球同步卫星,则a、c的角速度相等,根据v=ωr可知,线速度关系va
9.选AD 设三星系统Ⅰ中等边三角形的边长为L,则三星系统Ⅱ中等边三角形的边长为qL,根据万有引力提供向心力可得 =ma=m=mω2×, =kma′=km=kmω′2×,所以系统Ⅱ中一个星球受到的合力是系统Ⅰ中一个星球受到的合力的=倍,系统Ⅱ中一个星球的加速度是系统Ⅰ中一个星球的加速度的==倍,系统Ⅱ中一个星球的角速度是系统Ⅰ中一个星球的角速度的==倍,系统Ⅱ中一个星球的线速度是系统Ⅰ中一个星球的线速度的== 倍,故选A、D。
10.选AC 根据变轨原理,飞船在圆轨道Ⅰ的A点需加速做离心运动进入椭圆轨道Ⅱ,故飞船在椭圆轨道Ⅱ经过A点的速度大于飞船在圆轨道Ⅰ经过A点的速度,故A正确;第一宇宙速度为7.9 km/s,是最大环绕速度,故飞船在椭圆轨道Ⅱ经过A点的速度一定小于7.9 km/s,故B错误;根据牛顿第二定律有G=ma,故飞船在椭圆轨道Ⅱ经过A点的加速度与飞船在圆轨道Ⅰ经过A点的加速度大小相等,故C正确;根据万有引力与重力的关系G=mg,根据万有引力提供向心力有G=m(R+h),解得飞船在轨道Ⅲ的周期为T=,根据开普勒第三定律=k,由轨道Ⅱ的半长轴小于轨道Ⅲ的半径,可知飞船在轨道Ⅱ的周期TⅡ小于轨道Ⅲ的周期T,飞船沿轨道Ⅱ由A点到B点的时间为t=TⅡ
解得T火=CT。
(2)由题意得ω地Δt=ω火Δt+2π
由角速度和周期关系得Δt=Δt+2π
解得Δt=。
答案:(1)CT (2)
12.解析:(1)设质量为m0的物体在北极地面静止,则m0g0=G,解得M=。
(2)设货物质量为m,在距地面高3R站点受到的万有引力为F,则F=G,货物绕地球做匀速圆周运动,设太空电梯对货物的支持力为N,则F-N=mω2·4R
N=mg
ω=
联立解得g=-。
答案:(1) (2)-
13.解析:(1)设月球表面重力加速度为g,由平抛运动规律有
h=gt2,x=v0t
解得g=。
(2)在月球表面的物体受到的重力等于万有引力mg=G
解得M=
月球的第一宇宙速度为近月卫星的运行速度,根据重力提供向心力有mg=m
解得v1== 。
(3)月球的平均密度ρ===。
答案:(1) (2) (3)
14.解析:(1)地球表面一质量为m的物体,其受到的万有引力等于重力,所以有=mg
解得地球质量为M=
则地球的平均密度为ρ===。
(2)空间站绕地球做匀速圆周运动,由万有引力提供向心力,所以有=m·(R+h)
解得周期为T=2π。
(3)设空间站与同步卫星的轨道半径分别为r1和r2,运行周期分别为T1和T2,由开普勒第三定律可得=
则根据题意可知,空间站与同步卫星的轨道半径分别为
r1=R+=R=17h
r2=R+×90=R=106h
可以得到空间站的周期为
T1== h≈1.5 h。
答案:(1) (2)2π (3)1.5小时
7 / 7
