2025秋期浙教版数学九年级上册期中考试试卷(含答案)
文档属性
| 名称 | 2025秋期浙教版数学九年级上册期中考试试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 11:36:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025秋期浙教版数学九年级上册期中考试试卷
一、单选题(共10题;共20分)
1.(2分)(2024九上·合江月考)将二次函数化为的形式为( )
A. B. C. D.
2.(2分)(2020八下·无锡期中)对于“a,b都是实数,则(a-b)2≥0”这一事件是( )
A.必然事件 B.不确定事件 C.不可能事件 D.随机事件
3.(2分)(2022·海珠模拟)若二次函数,当时,,则a的值是( )
A.1 B. C. D.﹣1
4.(2分)(2023九上·巴东月考)如图,在同一直角坐标系下,一次函数与二次函数的图象可能是( )
A. B.
C. D.
5.(2分)(2024七下·长安期末)四张完全相同的卡片上,分别画有等边三角形、矩形、菱形、正五边形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为( )
A. B. C. D.1
6.(2分)(2023九上·邕宁期中)将二次函数的图象向下平移2个单位,再向右平移3个单位,则平移后的二次函数的解析式为( )
A. B.
C. D.
7.(2分)(2024九上·潮阳月考)已知二次函数的图象如图所示,在下列5个结论:①;②;③;④;⑤的实数),其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
8.(2分)(2021九上·阳东期末)两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,正面朝上的概率
B.掷一枚正六面体的骰子,出现 点的概率
C.转动如图所示的转盘,转到数字为奇数的概率
D.从装有 个红球和 个蓝球的口袋中任取一个球恰好是蓝球的概率
9.(2分)(2022·广州)如图,抛物线的对称轴为,下列结论正确的是( )
A. B.
C.当时,y随x的增大而减小 D.当时,y随x的增大而减小
10.(2分)(2024·宁波模拟)已知:,,,则下列说法中正确的是 ( )
A.有最大值4,最小值1 B.有最大值3,最小值
C.有最大值3,最小值1 D.有最大值3,最小值
二、填空题(共6题;共18分)
11.(3分)(2019九上·镇江期末)若二次函数y=(m+1)x|m|+4x﹣16的图象开口向下,则m= .
12.(3分)(2024九下·虹口模拟)将抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为 .
13.(3分)(2025·闵行模拟)某印刷厂10月份印书20万册,如果第四季度从11月份起,每月的印书量的增长率都为,如果设12月份比10月份多印了万册,那么关于的函数解析式是 .(不写定义域)
14.(3分)(2021七下·大连期末)一个不透明的盒子中有若干个白球和个黑球,从中摸出一球记下颜色后放回,重复摸球次,其中摸到黑球的次数为次,盒中有白球约 个.
15.(3分)已知二次函数 , 若 , 则函数 的最大值为 (用 表示).
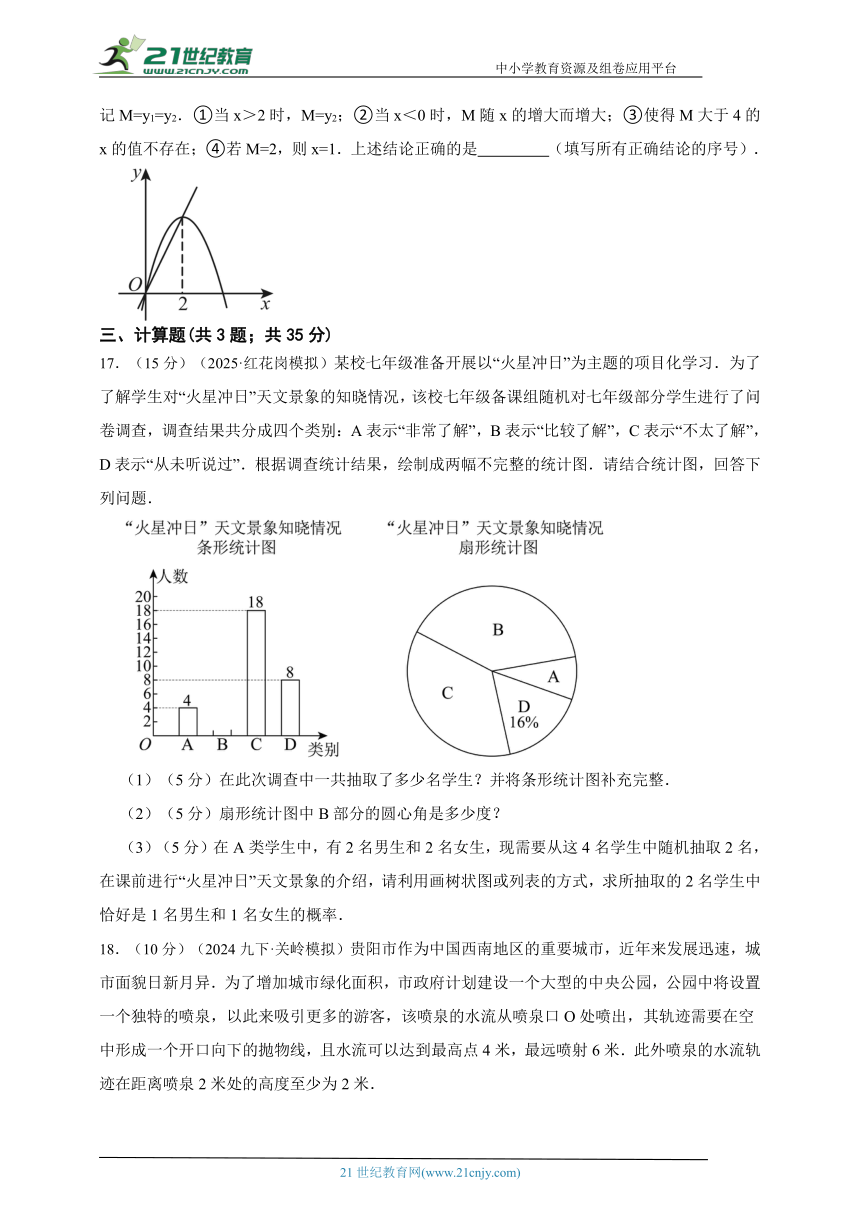
16.(3分)(2023九上·椒江月考)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是 (填写所有正确结论的序号).
三、计算题(共3题;共35分)
17.(15分)(2025·红花岗模拟)某校七年级准备开展以“火星冲日”为主题的项目化学习.为了了解学生对“火星冲日”天文景象的知晓情况,该校七年级备课组随机对七年级部分学生进行了问卷调查,调查结果共分成四个类别:A表示“非常了解”,B表示“比较了解”,C表示“不太了解”,D表示“从未听说过”.根据调查统计结果,绘制成两幅不完整的统计图.请结合统计图,回答下列问题.
(1)(5分)在此次调查中一共抽取了多少名学生?并将条形统计图补充完整.
(2)(5分)扇形统计图中B部分的圆心角是多少度?
(3)(5分)在A类学生中,有2名男生和2名女生,现需要从这4名学生中随机抽取2名,在课前进行“火星冲日”天文景象的介绍,请利用画树状图或列表的方式,求所抽取的2名学生中恰好是1名男生和1名女生的概率.
18.(10分)(2024九下·关岭模拟)贵阳市作为中国西南地区的重要城市,近年来发展迅速,城市面貌日新月异.为了增加城市绿化面积,市政府计划建设一个大型的中央公园,公园中将设置一个独特的喷泉,以此来吸引更多的游客,该喷泉的水流从喷泉口O处喷出,其轨迹需要在空中形成一个开口向下的抛物线,且水流可以达到最高点4米,最远喷射6米.此外喷泉的水流轨迹在距离喷泉2米处的高度至少为2米.
(1)(5分)请你计算出该抛物线的表达式;
(2)(5分)验证在距离喷泉2米处水流的高度是否满足要求.
19.(10分)(2024九下·芙蓉模拟)如图,抛物线(),与x轴交于、O两点,为抛物线的顶点.
(1)(5分)求该抛物线的解析式;
(2)(5分)点E为的中点,以点E为圆心、以1为半径作,交x轴于B、C两点
①射线交抛物线于点P,若,求点P的坐标;
②如图2,连接,取的中点N,则线段的长度是否存在最大值或最小值?若存在,请求出的最值,请说明理由.
四、解答题(共4题;共47分)
20.(10分)(2024·泗阳模拟)一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上.
(1)(5分)甲坐在②号座位的概率是____________;
(2)(5分)用画树状图或列表等方法,求甲与乙相邻而坐的概率.
21.(10分)(2024·柴桑模拟)某市共青团委员会本着“受教育、长才干、作贡献”的宗旨,组织了大学生返回家乡参与社会实践的活动,并计划让某校学生从“A.条幅标语”“B.互联网推广”“C.宣传橱窗”“D.挂图海报”中随机选择一种宣传方式,对本次活动进行宣传.
(1)(5分)若小贤参与了此次活动的宣传,则他选择“D.挂图海报”的概率是 .
(2)(5分)若在选择“B.互联网推广”的学生中选取3名学生,在选择“C.宣传橱窗”的学生中选取1名学生,从选取的这4名学生中任选2名分享宣传经验,请用画树状图法或列表法,求选取的2名学生恰好都是选择“B.互联网推广”的概率.
22.(6分)一个不透明的口袋中有三个小球,上面分别标有字母A,B,C,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用画树状图(或列表)的方法,求该同学两次摸出的小球所标字母相同的概率.
23.(21分)(2025·玉林模拟)我们约定:若两条抛物线与轴有两个相同的交点,且开口方向相反,我们就把两条抛物线构成的封闭曲线叫做“山水线”,如图所示.根据约定,解答下列问题:
(1)(7分)判断下列每组的两条抛物线是否构成“山水线”.若是,请在横线上画“√”;若不是,请在横线上画“×”.
①和;________
②和;________
③和.________
(2)(7分)若抛物线和抛物线恰好构成“山水线”,求的值.
(3)(7分)若抛物线和构成的“山水线”关于轴对称,该“山水线”与轴交于点,,点在点左侧.设点,是线段上的动点,过点作轴的垂线交该“山水线”于点,,过点作轴的垂线交该“山水线”于点,,点,在轴下方.试探究:是否存在以线段长为斜边、线段,长为直角边的等腰直角三角形?若存在,请求出该三角形的面积;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
2.【答案】A
【知识点】事件的分类
3.【答案】D
【知识点】二次函数y=ax²+bx+c的性质
4.【答案】C
【知识点】二次函数图象与系数的关系
5.【答案】B
【知识点】中心对称及中心对称图形;概率公式
6.【答案】D
【知识点】二次函数图象的几何变换
7.【答案】D
【知识点】二次函数图象与系数的关系
8.【答案】D
【知识点】概率的意义
9.【答案】C
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
10.【答案】C
【知识点】反比例函数的性质;二次函数的最值;二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
11.【答案】﹣2
【知识点】二次函数的定义;二次函数y=ax²+bx+c的性质
12.【答案】
【知识点】二次函数图象的几何变换
13.【答案】
【知识点】函数解析式;二次函数的实际应用-百分率问题
14.【答案】15
【知识点】概率的简单应用
15.【答案】18a
【知识点】二次函数的最值;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
16.【答案】②③
【知识点】二次函数图象与系数的关系
17.【答案】(1)解:此次调查中一共抽取的学生人数为:(名)
(名),
补充条形统计图如图所示:
(2)解:
答:扇形统计图中部分的圆心角是.
(3)解:画树状图如下:
共有12种等可能的结果,其中恰好是一名男生和一名女生的结果有8种,
所抽取的2名学生中恰好是一名男生和一名女生的概率是.
【知识点】扇形统计图;条形统计图;用列表法或树状图法求概率
18.【答案】(1)
(2)符合要求
【知识点】二次函数的实际应用-喷水问题
19.【答案】(1)
(2)①点或②的最大值为,最小值为
【知识点】待定系数法求二次函数解析式;勾股定理;三角形的中位线定理
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
22.【答案】解:列表得:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由列表可知可能出现的结果共9种,其中两次摸出的小球所标字母相同的情况数有3种,所以该同学两次摸出的小球所标字母相同的概率= =
【知识点】用列表法或树状图法求概率
23.【答案】(1)①×,②√;③√;
(2)2;
(3)存在,2.
【知识点】二次函数图象与坐标轴的交点问题;等腰三角形的判定与性质;勾股定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025秋期浙教版数学九年级上册期中考试试卷
一、单选题(共10题;共20分)
1.(2分)(2024九上·合江月考)将二次函数化为的形式为( )
A. B. C. D.
2.(2分)(2020八下·无锡期中)对于“a,b都是实数,则(a-b)2≥0”这一事件是( )
A.必然事件 B.不确定事件 C.不可能事件 D.随机事件
3.(2分)(2022·海珠模拟)若二次函数,当时,,则a的值是( )
A.1 B. C. D.﹣1
4.(2分)(2023九上·巴东月考)如图,在同一直角坐标系下,一次函数与二次函数的图象可能是( )
A. B.
C. D.
5.(2分)(2024七下·长安期末)四张完全相同的卡片上,分别画有等边三角形、矩形、菱形、正五边形,现从中随机抽取一张,卡片上画的恰好是中心对称图形的概率为( )
A. B. C. D.1
6.(2分)(2023九上·邕宁期中)将二次函数的图象向下平移2个单位,再向右平移3个单位,则平移后的二次函数的解析式为( )
A. B.
C. D.
7.(2分)(2024九上·潮阳月考)已知二次函数的图象如图所示,在下列5个结论:①;②;③;④;⑤的实数),其中正确的结论有( )
A.5个 B.4个 C.3个 D.2个
8.(2分)(2021九上·阳东期末)两名同学在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制出统计图如图所示,则符合这一结果的试验可能是( )
A.抛一枚硬币,正面朝上的概率
B.掷一枚正六面体的骰子,出现 点的概率
C.转动如图所示的转盘,转到数字为奇数的概率
D.从装有 个红球和 个蓝球的口袋中任取一个球恰好是蓝球的概率
9.(2分)(2022·广州)如图,抛物线的对称轴为,下列结论正确的是( )
A. B.
C.当时,y随x的增大而减小 D.当时,y随x的增大而减小
10.(2分)(2024·宁波模拟)已知:,,,则下列说法中正确的是 ( )
A.有最大值4,最小值1 B.有最大值3,最小值
C.有最大值3,最小值1 D.有最大值3,最小值
二、填空题(共6题;共18分)
11.(3分)(2019九上·镇江期末)若二次函数y=(m+1)x|m|+4x﹣16的图象开口向下,则m= .
12.(3分)(2024九下·虹口模拟)将抛物线先向右平移3个单位,再向下平移4个单位后,所得到的新抛物线的表达式为 .
13.(3分)(2025·闵行模拟)某印刷厂10月份印书20万册,如果第四季度从11月份起,每月的印书量的增长率都为,如果设12月份比10月份多印了万册,那么关于的函数解析式是 .(不写定义域)
14.(3分)(2021七下·大连期末)一个不透明的盒子中有若干个白球和个黑球,从中摸出一球记下颜色后放回,重复摸球次,其中摸到黑球的次数为次,盒中有白球约 个.
15.(3分)已知二次函数 , 若 , 则函数 的最大值为 (用 表示).
16.(3分)(2023九上·椒江月考)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是 (填写所有正确结论的序号).
三、计算题(共3题;共35分)
17.(15分)(2025·红花岗模拟)某校七年级准备开展以“火星冲日”为主题的项目化学习.为了了解学生对“火星冲日”天文景象的知晓情况,该校七年级备课组随机对七年级部分学生进行了问卷调查,调查结果共分成四个类别:A表示“非常了解”,B表示“比较了解”,C表示“不太了解”,D表示“从未听说过”.根据调查统计结果,绘制成两幅不完整的统计图.请结合统计图,回答下列问题.
(1)(5分)在此次调查中一共抽取了多少名学生?并将条形统计图补充完整.
(2)(5分)扇形统计图中B部分的圆心角是多少度?
(3)(5分)在A类学生中,有2名男生和2名女生,现需要从这4名学生中随机抽取2名,在课前进行“火星冲日”天文景象的介绍,请利用画树状图或列表的方式,求所抽取的2名学生中恰好是1名男生和1名女生的概率.
18.(10分)(2024九下·关岭模拟)贵阳市作为中国西南地区的重要城市,近年来发展迅速,城市面貌日新月异.为了增加城市绿化面积,市政府计划建设一个大型的中央公园,公园中将设置一个独特的喷泉,以此来吸引更多的游客,该喷泉的水流从喷泉口O处喷出,其轨迹需要在空中形成一个开口向下的抛物线,且水流可以达到最高点4米,最远喷射6米.此外喷泉的水流轨迹在距离喷泉2米处的高度至少为2米.
(1)(5分)请你计算出该抛物线的表达式;
(2)(5分)验证在距离喷泉2米处水流的高度是否满足要求.
19.(10分)(2024九下·芙蓉模拟)如图,抛物线(),与x轴交于、O两点,为抛物线的顶点.
(1)(5分)求该抛物线的解析式;
(2)(5分)点E为的中点,以点E为圆心、以1为半径作,交x轴于B、C两点
①射线交抛物线于点P,若,求点P的坐标;
②如图2,连接,取的中点N,则线段的长度是否存在最大值或最小值?若存在,请求出的最值,请说明理由.
四、解答题(共4题;共47分)
20.(10分)(2024·泗阳模拟)一张圆桌旁设有4个座位,丙先坐在了如图所示的座位上,甲、乙2人等可能地坐到①、②、③中的2个座位上.
(1)(5分)甲坐在②号座位的概率是____________;
(2)(5分)用画树状图或列表等方法,求甲与乙相邻而坐的概率.
21.(10分)(2024·柴桑模拟)某市共青团委员会本着“受教育、长才干、作贡献”的宗旨,组织了大学生返回家乡参与社会实践的活动,并计划让某校学生从“A.条幅标语”“B.互联网推广”“C.宣传橱窗”“D.挂图海报”中随机选择一种宣传方式,对本次活动进行宣传.
(1)(5分)若小贤参与了此次活动的宣传,则他选择“D.挂图海报”的概率是 .
(2)(5分)若在选择“B.互联网推广”的学生中选取3名学生,在选择“C.宣传橱窗”的学生中选取1名学生,从选取的这4名学生中任选2名分享宣传经验,请用画树状图法或列表法,求选取的2名学生恰好都是选择“B.互联网推广”的概率.
22.(6分)一个不透明的口袋中有三个小球,上面分别标有字母A,B,C,除所标字母不同外,其它完全相同,从中随机摸出一个小球,记下字母后放回并搅匀,再随机摸出一个小球,用画树状图(或列表)的方法,求该同学两次摸出的小球所标字母相同的概率.
23.(21分)(2025·玉林模拟)我们约定:若两条抛物线与轴有两个相同的交点,且开口方向相反,我们就把两条抛物线构成的封闭曲线叫做“山水线”,如图所示.根据约定,解答下列问题:
(1)(7分)判断下列每组的两条抛物线是否构成“山水线”.若是,请在横线上画“√”;若不是,请在横线上画“×”.
①和;________
②和;________
③和.________
(2)(7分)若抛物线和抛物线恰好构成“山水线”,求的值.
(3)(7分)若抛物线和构成的“山水线”关于轴对称,该“山水线”与轴交于点,,点在点左侧.设点,是线段上的动点,过点作轴的垂线交该“山水线”于点,,过点作轴的垂线交该“山水线”于点,,点,在轴下方.试探究:是否存在以线段长为斜边、线段,长为直角边的等腰直角三角形?若存在,请求出该三角形的面积;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
2.【答案】A
【知识点】事件的分类
3.【答案】D
【知识点】二次函数y=ax²+bx+c的性质
4.【答案】C
【知识点】二次函数图象与系数的关系
5.【答案】B
【知识点】中心对称及中心对称图形;概率公式
6.【答案】D
【知识点】二次函数图象的几何变换
7.【答案】D
【知识点】二次函数图象与系数的关系
8.【答案】D
【知识点】概率的意义
9.【答案】C
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
10.【答案】C
【知识点】反比例函数的性质;二次函数的最值;二次函数y=a(x-h)²+k的性质;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
11.【答案】﹣2
【知识点】二次函数的定义;二次函数y=ax²+bx+c的性质
12.【答案】
【知识点】二次函数图象的几何变换
13.【答案】
【知识点】函数解析式;二次函数的实际应用-百分率问题
14.【答案】15
【知识点】概率的简单应用
15.【答案】18a
【知识点】二次函数的最值;二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
16.【答案】②③
【知识点】二次函数图象与系数的关系
17.【答案】(1)解:此次调查中一共抽取的学生人数为:(名)
(名),
补充条形统计图如图所示:
(2)解:
答:扇形统计图中部分的圆心角是.
(3)解:画树状图如下:
共有12种等可能的结果,其中恰好是一名男生和一名女生的结果有8种,
所抽取的2名学生中恰好是一名男生和一名女生的概率是.
【知识点】扇形统计图;条形统计图;用列表法或树状图法求概率
18.【答案】(1)
(2)符合要求
【知识点】二次函数的实际应用-喷水问题
19.【答案】(1)
(2)①点或②的最大值为,最小值为
【知识点】待定系数法求二次函数解析式;勾股定理;三角形的中位线定理
20.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
21.【答案】(1)
(2)
【知识点】用列表法或树状图法求概率;概率公式
22.【答案】解:列表得:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由列表可知可能出现的结果共9种,其中两次摸出的小球所标字母相同的情况数有3种,所以该同学两次摸出的小球所标字母相同的概率= =
【知识点】用列表法或树状图法求概率
23.【答案】(1)①×,②√;③√;
(2)2;
(3)存在,2.
【知识点】二次函数图象与坐标轴的交点问题;等腰三角形的判定与性质;勾股定理
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
