【巩固复习】第六单元 圆(培优卷.含解析)五年级下册数学苏教版
文档属性
| 名称 | 【巩固复习】第六单元 圆(培优卷.含解析)五年级下册数学苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 537.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 23:01:55 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第六单元 圆
一、选择题
1.车轮做成圆的,车轴应装在( )。
A.圆心位置 B.圆上任何位置 C.圆内任何位置 D.圆的直径上
2.在一个边长是4dm的正方形内画一个最大的圆,这个圆的周长是( )dm。
A.12.56 B.6.28 C.10.28 D.25.12
3.甲、乙两只蚂蚁以同样的速度,同时从点A出发,甲蚂蚁沿着正方形走,乙蚂蚁沿着圆形走,( )回到起点。
A.甲先 B.乙先 C.同时
4.小明画了一个半径4厘米的圆,再以这个圆的半径为直径画了一个小圆,小圆的面积是大圆面积的( )。
A. B. C. D.无法确定
5.从一张长14厘米、宽10厘米的长方形卡纸上剪下一个最大的圆,圆的面积是( )平方厘米。
A.78.5 B.62.8 C.153.86
6.下面三个图形中(单位:厘米),周长最长的是( )。
A. B. C.
二、填空题
7.每当唐僧念一声紧箍咒,孙悟空头上的金箍就会缩短0.314厘米,此时孙悟空头上的金箍半径将减少( )厘米。
8.如图,平行四边形的面积比长方形的面积小6cm2,则圆的面积是( )cm2。
9.有一个三角形,它的面积与直径是2厘米的圆的面积正好相等。已知三角形的底是3.14厘米。它的高是( )厘米。(π取3.14)
10.如图,三角形ABC是直角三角形,AB是圆的直径,AB长10厘米,已知阴影乙部分比阴影甲部分的面积少6平方厘米。那么BC的长是( )厘米,三角形ABC的面积是( )平方厘米。
三、判断题
11.一个圆的半径是3厘米,它的直径是6厘米。( )
12.圆的周长正好是它的直径的3.14倍。( )
13.一个圆环滚动一周前进的距离等于圆环的周长。( )
14.把半径的圆等分成若干份,拼成一个近似的长方形后,长方形的周长比圆的周长长。( )
15.圆的半径增加2倍,则周长增加2倍,面积增加4倍。( )
16.如果几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长。( )
四、计算题
17.口算下面各题,并熟记它们的结果。
3.14×1= 3.14×2= 3.14×3=
3.14×4= 3.14×5= 3.14×6=
3.14×7= 3.14×8= 3.14×9=
18.求下面各图阴影部分的面积。(单位:cm)
19.如图中大圆的半径是小圆的直径,请你计算下面图形阴影部分的面积。
五、作图题
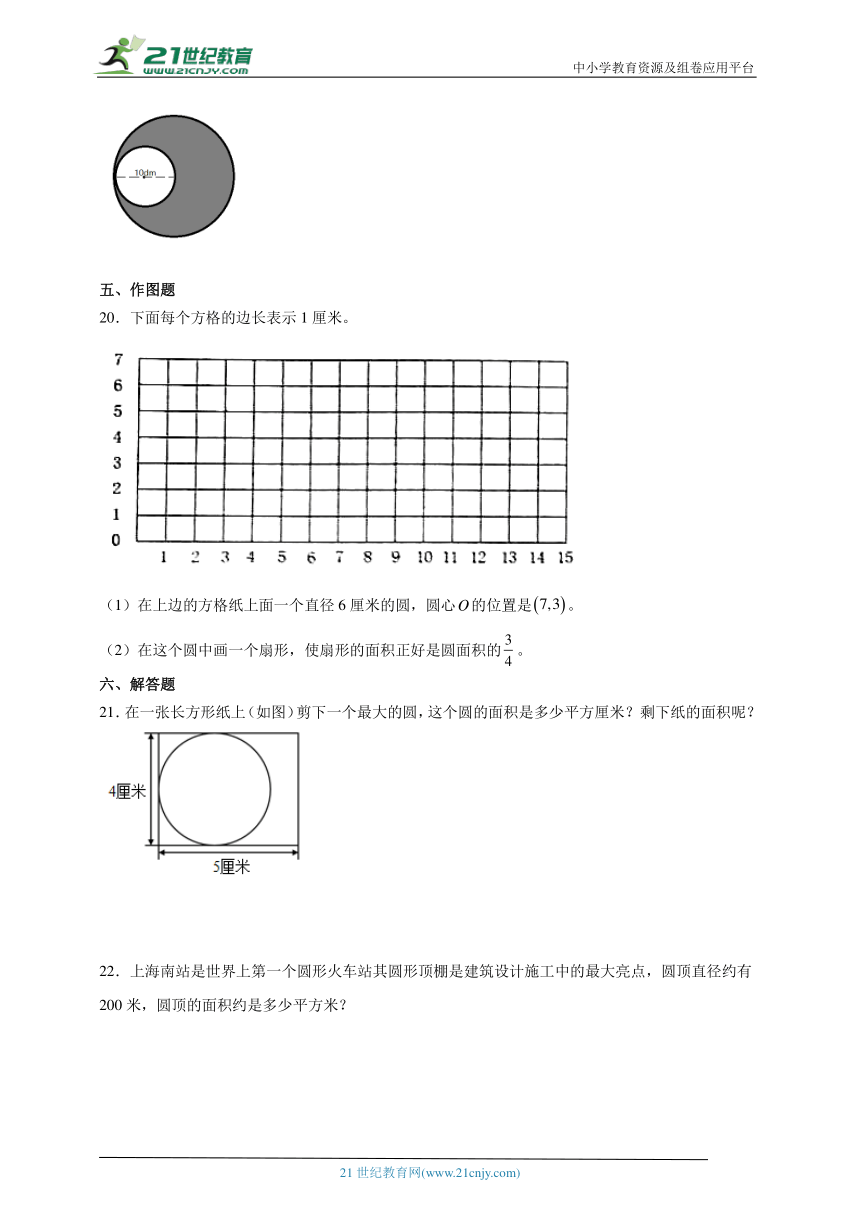
20.下面每个方格的边长表示1厘米。
(1)在上边的方格纸上面一个直径6厘米的圆,圆心的位置是。
(2)在这个圆中画一个扇形,使扇形的面积正好是圆面积的。
六、解答题
21.在一张长方形纸上(如图)剪下一个最大的圆,这个圆的面积是多少平方厘米?剩下纸的面积呢?
22.上海南站是世界上第一个圆形火车站其圆形顶棚是建筑设计施工中的最大亮点,圆顶直径约有200米,圆顶的面积约是多少平方米?
23.在一块草地的木柱上拴着一头牛,拴牛的绳长为5米(拴在木桩上的绳子忽略不计),牛最多可吃到草的面积是多少平方米?
24.中国生态环境保护吉祥物为一对名为“小山”和“小水”的卡通形象,以“青山绿水”为设计原型,有机结合“绿叶、花朵、云纹、水纹”等设计元素,表达出“绿水青山就是金山银山”的理念。刘阿姨绣了一幅“小山”和“小水”十字绣,她把这幅十字绣装裱在圆形铝合金镜框中,用了1.884米长的铝合金条,这幅十字绣的半径是多少厘米?
25.沙子堆在地面上占地正好是圆形,量出它一周的长度是15.7米,那么直径是多少米?
为迎接世博,某街道铺设一块草坪,草坪的形状如图所示,若每平方米的铺设费用是100元,则街道铺设该草坪需要多少费用?
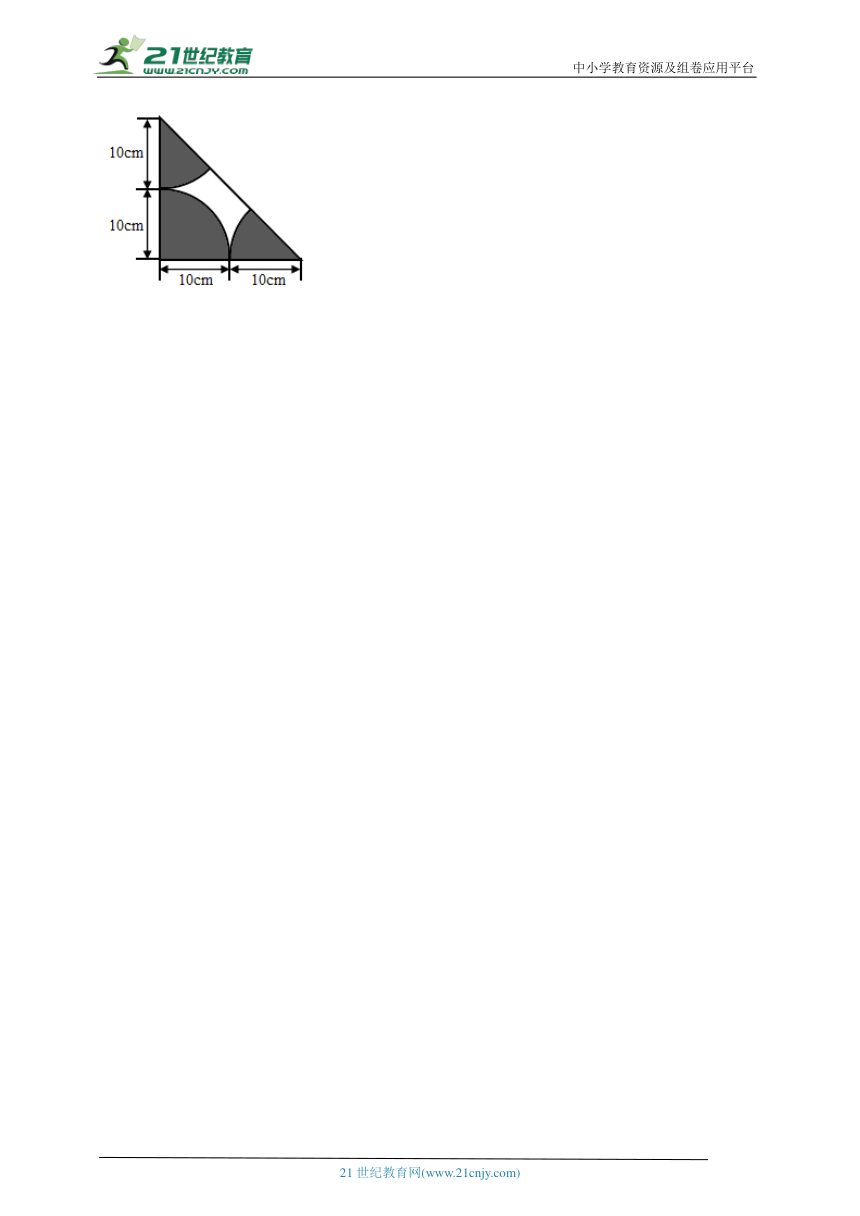
27.实验小学举行“最美班级”评比活动,王宁从一块三角形纸板上剪下3个扇形布置教室(如图)。这3个扇形的面积和是多少平方厘米?
答案与解析
1.A
【解题思路】连接圆心和圆上任意一点的线段叫做半径。半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。
把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【解答过程】车轮做成圆的,车轴应装在圆心位置。
故答案为:A
2.A
【解题思路】根据题意,在一个边长是4dm的正方形内画一个最大的圆,那么这个圆的直径等于正方形的边长;根据圆的周长公式C=πd,求出这个圆的周长。
【解答过程】3.14×4=12.56(dm)
这个圆的周长是12.56dm。
故答案为:A
3.B
【解题思路】设正方形的边长是1,从图中可知:正方形的边长=圆的直径,根据正方形的周长=边长×4,圆的周长:C=πd,分别代入数据计算,再判断即可。
【解答过程】设正方形的边长是1。
甲:1×4=4
乙:1×3.14=3.14
4>3.14
乙先回到起点。
故答案为:B
4.B
【解答过程】由题意可知小圆的直径是4厘米,由此得出小圆的半径,根据圆的面积=πr2,小圆面积÷大圆面积即可。
【解答过程】由分析可得:πr2÷πR2=r2÷R2=(4÷2)2÷16=,故选择:B。
【要点提示】如果小圆半径是大圆半径的 ,则小圆面积是大圆面积的 。
5.A
【解题思路】根据题意可知:在这张长方形纸上剪一个最大的圆,圆的直径等于长方形的宽,根据同圆或等圆直径与半径的关系,r=,圆的面积公式:S=πr2,把数据代入公式解答。
【解答过程】10÷2=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
故答案为:A
【要点提示】此题考查的目的是理解掌握同圆或等圆直径与半径的关系及应用,圆的面积公式及应用。
6.A
【解题思路】正方形的周长=边长×4,三角形周长等于三边的长度之和,圆的周长C,据此把每个图形的周长求出来,再比较即可。
【解答过程】
A.的周长是(厘米);
B.的周长是(厘米);
C.的周长是(厘米);
所以三个图形中(单位:厘米),周长最长的是。
故答案为:
【要点提示】本题考查正方形、三角形、圆的周长,解答本题的关键是掌握这些图形周长的计算公式。
7.0.05
【解题思路】缩短0.314厘米,圆的周长就会减少0.314厘米,根据圆的周长公式:C=,代入数据,即可求出半径缩短了多少厘米。
【解答过程】0.314÷2÷3.14
=0.157÷3.14
=0.05(厘米)
【要点提示】此题的解题关键是灵活运用圆的周长公式解决实际的问题。
8.28.26
【解题思路】平行四边形面积=底×高,长方形面积=长×宽,观察图发现平行四边形的高和长方形的长相等,则平行四边形的面积比长方形面积小的部分=高×(平行四边形的底-长方形的宽),据此求出平行四边形的高;圆的直径等于平行四边形的高,再根据圆的面积,求出圆的面积。
【解答过程】直径:6÷(5-4)
=6÷1
=6(厘米)
圆的面积:3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
所以圆的面积是28.26平方厘米。
9.2
【解题思路】先利用圆的面积公式S=πr 求出圆的面积,也就是三角形的面积,进而利用三角形的高=三角形的面积×2÷底,即可求出高。
【解答过程】3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
3.14×2÷3.14
=6.28÷3.14
=2(厘米)
【要点提示】此题主要考查圆和三角形的面积的计算方法的灵活应用。
10. 6.65 33.25
【解题思路】看图可知,半圆的面积-三角形ABC的面积是=阴影甲部分的面积-阴影乙部分的面积=6平方厘米,设BC的长是x厘米,根据半圆的面积-三角形ABC的面积是=6平方厘米,列出方程求出x的值是BC的长,再根据三角形面积=底×高÷2,求出三角形ABC的面积。
【解答过程】解:设BC的长是x厘米。
3.14×(10÷2)2÷2-10x÷2=6
3.14×52÷2-5x=6
3.14×25÷2-5x=6
39.25-5x+5x=6+5x
6+5x=39.25
6+5x-6=39.25-6
5x=33.25
5x÷5=33.25÷5
x=6.65
10×6.65÷2=33.25(平方厘米)
BC的长是6.65厘米,三角形ABC的面积是33.25平方厘米。
【要点提示】关键是掌握并灵活运用圆和三角形面积公式,用方程解决问题的关键是找到等量关系。
11.√
【解题思路】在同一个圆或等圆中,直径是半径的2倍,半径是直径的一半,由此解答问题。
【解答过程】3×2=6(厘米)
一个圆的半径是3厘米,它的直径是6厘米。原说法正确。
故答案为:√
12.×
【解题思路】圆的周长和它的直径的比值是一个固定的数,我们叫它圆周率(π),也就是说圆的周长是它的直径的π倍,在实际应用时,我们常常取它的近似值,π≈3.14;π≠3.14,据此解答。
【解答过程】根据分析可知,圆的周长正好是它的直径的π倍。
原题干说法错误。
故答案为:×
13.√
【解题思路】围成圆的曲线的长叫做圆的周长。圆是曲面,要测量圆的周长,可以用线绕圆一周,然后将线拉直量出它的长度,即是圆的周长;也可以先在圆上选定一个点,滚动一周,测量前进的距离,即是这个圆的周长。
【解答过程】一个圆环滚动一周前进的距离等于圆环的周长。
原题说法正确。
故答案为:√
14.√
【解题思路】根据圆拼成长方形可知,近似长方形的长等于圆的周长的一半,宽等于圆的半径,根据长方形周长公式:(长+宽)×2,长方形周长=圆的周长+2×半径,据此解答。
【解答过程】根据分析可知,长方形周长=圆的周长+2×半径
长方形周长-圆的周长
=圆的周长+2×4-圆的周长
=8(cm)
把半径4cm的圆等分成若干份,拼成一个近似长方形,长方形的周长比圆的周长长8cm。
原题干说法正确。
故答案为:√
【要点提示】本题考查圆的周长公式与长方形周长公式的联系。
15.×
【解题思路】圆的周长C=,圆的面积S=,如果半径增加2倍就等于半径扩大了3倍,即可求出扩大后的周长和面积。
【解答过程】圆的半径增加2倍后为,增加后圆的周长:×=,所以周长增加了-=,增加了=2倍;
增加后圆的面积:S==,所以面积增加了-=,增加了=8倍。
故答案为:错误
【要点提示】此题考查的是圆的周长与半径之间的关系及圆的面积与半径之间的关系,解题的关键是半径增加了2倍,也就是扩大了3倍。
16.√
【解题思路】根据圆的周长公式:周长=π×直径;设大圆的直径为D;小圆的直径为d1、d2、d3、…dn;d1+d2+d3+…+dn=D;小圆的周长为πd1、πd2、πd3、…πdn;大圆的周长为πD。小圆的周长和=πd1+πd2+πd3+…+πdn,根据乘法分配律的逆运算,原式化为:π(d1+d2+d3+…+dn);即π(d1+d2+d3+…+dn)=πD,即几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长,据此解答。
【解答过程】根据分析可知,如果几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长。
原题干说法正确。
故答案为:√
17.3.14;6.28;9.42;
12.56;15.7;18.84;
21.98;25.12;28.26
【解答过程】略
18.(1)9.12cm ;(2)1.57cm
【解题思路】(1)画辅助线切割成如图:,可知每一个小阴影部分面积的一半=圆的面积减去等腰直角三角形的面积,图中阴影部分可以分解成8个这样的图形即可。
(2)已知三角形的内角和是180°,由题意得,图中3个阴影部分的面积可以拼成一个半径为1厘米的半圆。
【解答过程】(1)×3.14×(4÷2)-2×2×=1.14(cm ),1.14×8=9.12(cm );
(2)3.14×1÷2=1.57(cm )。
故答案为:(1)9.12cm ;(2)1.57cm
【要点提示】本题主要考查的是求不规则图形的面积。可以把组合的图形看成是几个基本图形的相加,也可以看成是一个图形减另一个图形。
19.235.5dm2
【解题思路】由题意可知,阴影部分面积等于大圆面积减去小圆的面积。
【解答过程】
(dm2)
20.
【解题思路】(1)根据数对先确定点O的位置,点O的位置是(7,3),即表示点O是第7列与第3行的交点,直径是6厘米,说明半径是6÷2=3(厘米),据此画圆即可。
(2)把一个圆的面积看作单位“1”,依据扇形的特征,把圆平均分成4个扇形,取其中的三份就是即可。
【解答过程】如图:
【要点提示】依据数对找准圆心的位置和根据直径确定半径的长度是解决此题的关键,注意画扇形的方法。
21.12.56平方厘米;7.44平方厘米
【解题思路】在这个长方形中剪一个最大圆,这个圆的直径等于长方形的宽,根据圆的面积公式:S=,把数据代入公式即可求出圆的面积,再根据长方形的面积公式:S=ab,把数据代入公式求出长方形与圆的面积差即可求出剩余部分的面积。
【解答过程】4÷2=2(厘米)
3.14×22=3.14×4=12.56(平方厘米)
4×5-12.56
=20-12.56
=7.44(平方厘米)
答:这个圆的面积是12.56平方厘米,剩下纸的面积是7.44平方厘米。
【要点提示】此题主要考查圆的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
22.31400平方米
【解题思路】根据圆的面积公式求解即可。
【解答过程】
(平方米)
答:圆顶的面积约是31400平方米。
【要点提示】掌握圆的面积公式是解题的关键。
23.78.5平方米
【解题思路】牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积。
【解答过程】
(平方米)
答:牛所能吃到草的最大面积是78.5平方米。
【要点提示】本题主要考查圆的面积公式。能理解牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积是解题的关键。
24.30厘米
【解题思路】此题的1.884米,是用来裱画的铝合金条的长度,实际就是一个圆形的周长,转化成已知周长求半径,利用周长公式计算即可。
【解答过程】1.884米=188.4厘米
188.4÷3.14÷2
=30(厘米)
答:这幅十字绣的半径是30厘米。
【要点提示】这题考查的是学生在复杂的条件中,提取出简单的量,把前面修饰的语言概括成已知周长求半径这一个简单的数学问题。此题还要注意把题目中的单位进行统一,熟记圆的周长公式。
25.5米
【解题思路】由圆的周长=πd,所以直径d=周长÷π。
【解答过程】15.7÷3.14=5(米)
答:直径是5米。
【要点提示】此题主要考查的是圆的周长公式的灵活应用。
26.244200元
【解答过程】试题分析:根据题意,组合图形的面积等于长方形的面积加上两个圆的的面积,其中长方形的宽即为圆的半径,可根据长方形的面积公式和圆的面积公式进行计算可得到组合图形的面积,然后再用组合图形的面积乘100元即可得到铺设该草坪需要的总钱数,列式解答即可得到答案.
解:(30×50+3.14×302××2)×100
=(1500+3.14×900××2)×100,
=(1500+942)×100,
=2442×100,
=244200(元);
答:街道铺设该草坪需要244200元的费用.
点评:解答此题的关键是根据长方形的面积公式和圆的面积公式确定组合图形的面积.
27.157平方厘米
【解题思路】从图中得知:此三角形为等腰直角三角形,所以把这3个扇形拼在一起,能得到半径为5厘米的半圆,由此得出这3个扇形的面积和是半径为5厘米的半圆的面积;所以利用圆的面积公式S=πr2进行解答。
【解答过程】把这3个扇形拼在一起,能得到半径为5厘米的半圆;
3.14×102÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
答:这3个扇形的面积和是157平方厘米。
【要点提示】关键是根据图得出这3个扇形的面积和是半径为5厘米的半圆的面积,再利用圆的面积公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六单元 圆
一、选择题
1.车轮做成圆的,车轴应装在( )。
A.圆心位置 B.圆上任何位置 C.圆内任何位置 D.圆的直径上
2.在一个边长是4dm的正方形内画一个最大的圆,这个圆的周长是( )dm。
A.12.56 B.6.28 C.10.28 D.25.12
3.甲、乙两只蚂蚁以同样的速度,同时从点A出发,甲蚂蚁沿着正方形走,乙蚂蚁沿着圆形走,( )回到起点。
A.甲先 B.乙先 C.同时
4.小明画了一个半径4厘米的圆,再以这个圆的半径为直径画了一个小圆,小圆的面积是大圆面积的( )。
A. B. C. D.无法确定
5.从一张长14厘米、宽10厘米的长方形卡纸上剪下一个最大的圆,圆的面积是( )平方厘米。
A.78.5 B.62.8 C.153.86
6.下面三个图形中(单位:厘米),周长最长的是( )。
A. B. C.
二、填空题
7.每当唐僧念一声紧箍咒,孙悟空头上的金箍就会缩短0.314厘米,此时孙悟空头上的金箍半径将减少( )厘米。
8.如图,平行四边形的面积比长方形的面积小6cm2,则圆的面积是( )cm2。
9.有一个三角形,它的面积与直径是2厘米的圆的面积正好相等。已知三角形的底是3.14厘米。它的高是( )厘米。(π取3.14)
10.如图,三角形ABC是直角三角形,AB是圆的直径,AB长10厘米,已知阴影乙部分比阴影甲部分的面积少6平方厘米。那么BC的长是( )厘米,三角形ABC的面积是( )平方厘米。
三、判断题
11.一个圆的半径是3厘米,它的直径是6厘米。( )
12.圆的周长正好是它的直径的3.14倍。( )
13.一个圆环滚动一周前进的距离等于圆环的周长。( )
14.把半径的圆等分成若干份,拼成一个近似的长方形后,长方形的周长比圆的周长长。( )
15.圆的半径增加2倍,则周长增加2倍,面积增加4倍。( )
16.如果几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长。( )
四、计算题
17.口算下面各题,并熟记它们的结果。
3.14×1= 3.14×2= 3.14×3=
3.14×4= 3.14×5= 3.14×6=
3.14×7= 3.14×8= 3.14×9=
18.求下面各图阴影部分的面积。(单位:cm)
19.如图中大圆的半径是小圆的直径,请你计算下面图形阴影部分的面积。
五、作图题
20.下面每个方格的边长表示1厘米。
(1)在上边的方格纸上面一个直径6厘米的圆,圆心的位置是。
(2)在这个圆中画一个扇形,使扇形的面积正好是圆面积的。
六、解答题
21.在一张长方形纸上(如图)剪下一个最大的圆,这个圆的面积是多少平方厘米?剩下纸的面积呢?
22.上海南站是世界上第一个圆形火车站其圆形顶棚是建筑设计施工中的最大亮点,圆顶直径约有200米,圆顶的面积约是多少平方米?
23.在一块草地的木柱上拴着一头牛,拴牛的绳长为5米(拴在木桩上的绳子忽略不计),牛最多可吃到草的面积是多少平方米?
24.中国生态环境保护吉祥物为一对名为“小山”和“小水”的卡通形象,以“青山绿水”为设计原型,有机结合“绿叶、花朵、云纹、水纹”等设计元素,表达出“绿水青山就是金山银山”的理念。刘阿姨绣了一幅“小山”和“小水”十字绣,她把这幅十字绣装裱在圆形铝合金镜框中,用了1.884米长的铝合金条,这幅十字绣的半径是多少厘米?
25.沙子堆在地面上占地正好是圆形,量出它一周的长度是15.7米,那么直径是多少米?
为迎接世博,某街道铺设一块草坪,草坪的形状如图所示,若每平方米的铺设费用是100元,则街道铺设该草坪需要多少费用?
27.实验小学举行“最美班级”评比活动,王宁从一块三角形纸板上剪下3个扇形布置教室(如图)。这3个扇形的面积和是多少平方厘米?
答案与解析
1.A
【解题思路】连接圆心和圆上任意一点的线段叫做半径。半径决定圆的大小,在同一个圆内有无数条半径,同一个圆内所有的半径都相等。
把车轴安装在车轮的圆心处,车开起来更平稳,是利用了同一个圆的半径都相等的特性。
【解答过程】车轮做成圆的,车轴应装在圆心位置。
故答案为:A
2.A
【解题思路】根据题意,在一个边长是4dm的正方形内画一个最大的圆,那么这个圆的直径等于正方形的边长;根据圆的周长公式C=πd,求出这个圆的周长。
【解答过程】3.14×4=12.56(dm)
这个圆的周长是12.56dm。
故答案为:A
3.B
【解题思路】设正方形的边长是1,从图中可知:正方形的边长=圆的直径,根据正方形的周长=边长×4,圆的周长:C=πd,分别代入数据计算,再判断即可。
【解答过程】设正方形的边长是1。
甲:1×4=4
乙:1×3.14=3.14
4>3.14
乙先回到起点。
故答案为:B
4.B
【解答过程】由题意可知小圆的直径是4厘米,由此得出小圆的半径,根据圆的面积=πr2,小圆面积÷大圆面积即可。
【解答过程】由分析可得:πr2÷πR2=r2÷R2=(4÷2)2÷16=,故选择:B。
【要点提示】如果小圆半径是大圆半径的 ,则小圆面积是大圆面积的 。
5.A
【解题思路】根据题意可知:在这张长方形纸上剪一个最大的圆,圆的直径等于长方形的宽,根据同圆或等圆直径与半径的关系,r=,圆的面积公式:S=πr2,把数据代入公式解答。
【解答过程】10÷2=5(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
故答案为:A
【要点提示】此题考查的目的是理解掌握同圆或等圆直径与半径的关系及应用,圆的面积公式及应用。
6.A
【解题思路】正方形的周长=边长×4,三角形周长等于三边的长度之和,圆的周长C,据此把每个图形的周长求出来,再比较即可。
【解答过程】
A.的周长是(厘米);
B.的周长是(厘米);
C.的周长是(厘米);
所以三个图形中(单位:厘米),周长最长的是。
故答案为:
【要点提示】本题考查正方形、三角形、圆的周长,解答本题的关键是掌握这些图形周长的计算公式。
7.0.05
【解题思路】缩短0.314厘米,圆的周长就会减少0.314厘米,根据圆的周长公式:C=,代入数据,即可求出半径缩短了多少厘米。
【解答过程】0.314÷2÷3.14
=0.157÷3.14
=0.05(厘米)
【要点提示】此题的解题关键是灵活运用圆的周长公式解决实际的问题。
8.28.26
【解题思路】平行四边形面积=底×高,长方形面积=长×宽,观察图发现平行四边形的高和长方形的长相等,则平行四边形的面积比长方形面积小的部分=高×(平行四边形的底-长方形的宽),据此求出平行四边形的高;圆的直径等于平行四边形的高,再根据圆的面积,求出圆的面积。
【解答过程】直径:6÷(5-4)
=6÷1
=6(厘米)
圆的面积:3.14×(6÷2)2
=3.14×9
=28.26(平方厘米)
所以圆的面积是28.26平方厘米。
9.2
【解题思路】先利用圆的面积公式S=πr 求出圆的面积,也就是三角形的面积,进而利用三角形的高=三角形的面积×2÷底,即可求出高。
【解答过程】3.14×(2÷2)2
=3.14×1
=3.14(平方厘米)
3.14×2÷3.14
=6.28÷3.14
=2(厘米)
【要点提示】此题主要考查圆和三角形的面积的计算方法的灵活应用。
10. 6.65 33.25
【解题思路】看图可知,半圆的面积-三角形ABC的面积是=阴影甲部分的面积-阴影乙部分的面积=6平方厘米,设BC的长是x厘米,根据半圆的面积-三角形ABC的面积是=6平方厘米,列出方程求出x的值是BC的长,再根据三角形面积=底×高÷2,求出三角形ABC的面积。
【解答过程】解:设BC的长是x厘米。
3.14×(10÷2)2÷2-10x÷2=6
3.14×52÷2-5x=6
3.14×25÷2-5x=6
39.25-5x+5x=6+5x
6+5x=39.25
6+5x-6=39.25-6
5x=33.25
5x÷5=33.25÷5
x=6.65
10×6.65÷2=33.25(平方厘米)
BC的长是6.65厘米,三角形ABC的面积是33.25平方厘米。
【要点提示】关键是掌握并灵活运用圆和三角形面积公式,用方程解决问题的关键是找到等量关系。
11.√
【解题思路】在同一个圆或等圆中,直径是半径的2倍,半径是直径的一半,由此解答问题。
【解答过程】3×2=6(厘米)
一个圆的半径是3厘米,它的直径是6厘米。原说法正确。
故答案为:√
12.×
【解题思路】圆的周长和它的直径的比值是一个固定的数,我们叫它圆周率(π),也就是说圆的周长是它的直径的π倍,在实际应用时,我们常常取它的近似值,π≈3.14;π≠3.14,据此解答。
【解答过程】根据分析可知,圆的周长正好是它的直径的π倍。
原题干说法错误。
故答案为:×
13.√
【解题思路】围成圆的曲线的长叫做圆的周长。圆是曲面,要测量圆的周长,可以用线绕圆一周,然后将线拉直量出它的长度,即是圆的周长;也可以先在圆上选定一个点,滚动一周,测量前进的距离,即是这个圆的周长。
【解答过程】一个圆环滚动一周前进的距离等于圆环的周长。
原题说法正确。
故答案为:√
14.√
【解题思路】根据圆拼成长方形可知,近似长方形的长等于圆的周长的一半,宽等于圆的半径,根据长方形周长公式:(长+宽)×2,长方形周长=圆的周长+2×半径,据此解答。
【解答过程】根据分析可知,长方形周长=圆的周长+2×半径
长方形周长-圆的周长
=圆的周长+2×4-圆的周长
=8(cm)
把半径4cm的圆等分成若干份,拼成一个近似长方形,长方形的周长比圆的周长长8cm。
原题干说法正确。
故答案为:√
【要点提示】本题考查圆的周长公式与长方形周长公式的联系。
15.×
【解题思路】圆的周长C=,圆的面积S=,如果半径增加2倍就等于半径扩大了3倍,即可求出扩大后的周长和面积。
【解答过程】圆的半径增加2倍后为,增加后圆的周长:×=,所以周长增加了-=,增加了=2倍;
增加后圆的面积:S==,所以面积增加了-=,增加了=8倍。
故答案为:错误
【要点提示】此题考查的是圆的周长与半径之间的关系及圆的面积与半径之间的关系,解题的关键是半径增加了2倍,也就是扩大了3倍。
16.√
【解题思路】根据圆的周长公式:周长=π×直径;设大圆的直径为D;小圆的直径为d1、d2、d3、…dn;d1+d2+d3+…+dn=D;小圆的周长为πd1、πd2、πd3、…πdn;大圆的周长为πD。小圆的周长和=πd1+πd2+πd3+…+πdn,根据乘法分配律的逆运算,原式化为:π(d1+d2+d3+…+dn);即π(d1+d2+d3+…+dn)=πD,即几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长,据此解答。
【解答过程】根据分析可知,如果几个圆的直径之和等于一个大圆的直径,那么这几个圆的周长之和一定等于这个大圆的周长。
原题干说法正确。
故答案为:√
17.3.14;6.28;9.42;
12.56;15.7;18.84;
21.98;25.12;28.26
【解答过程】略
18.(1)9.12cm ;(2)1.57cm
【解题思路】(1)画辅助线切割成如图:,可知每一个小阴影部分面积的一半=圆的面积减去等腰直角三角形的面积,图中阴影部分可以分解成8个这样的图形即可。
(2)已知三角形的内角和是180°,由题意得,图中3个阴影部分的面积可以拼成一个半径为1厘米的半圆。
【解答过程】(1)×3.14×(4÷2)-2×2×=1.14(cm ),1.14×8=9.12(cm );
(2)3.14×1÷2=1.57(cm )。
故答案为:(1)9.12cm ;(2)1.57cm
【要点提示】本题主要考查的是求不规则图形的面积。可以把组合的图形看成是几个基本图形的相加,也可以看成是一个图形减另一个图形。
19.235.5dm2
【解题思路】由题意可知,阴影部分面积等于大圆面积减去小圆的面积。
【解答过程】
(dm2)
20.
【解题思路】(1)根据数对先确定点O的位置,点O的位置是(7,3),即表示点O是第7列与第3行的交点,直径是6厘米,说明半径是6÷2=3(厘米),据此画圆即可。
(2)把一个圆的面积看作单位“1”,依据扇形的特征,把圆平均分成4个扇形,取其中的三份就是即可。
【解答过程】如图:
【要点提示】依据数对找准圆心的位置和根据直径确定半径的长度是解决此题的关键,注意画扇形的方法。
21.12.56平方厘米;7.44平方厘米
【解题思路】在这个长方形中剪一个最大圆,这个圆的直径等于长方形的宽,根据圆的面积公式:S=,把数据代入公式即可求出圆的面积,再根据长方形的面积公式:S=ab,把数据代入公式求出长方形与圆的面积差即可求出剩余部分的面积。
【解答过程】4÷2=2(厘米)
3.14×22=3.14×4=12.56(平方厘米)
4×5-12.56
=20-12.56
=7.44(平方厘米)
答:这个圆的面积是12.56平方厘米,剩下纸的面积是7.44平方厘米。
【要点提示】此题主要考查圆的面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
22.31400平方米
【解题思路】根据圆的面积公式求解即可。
【解答过程】
(平方米)
答:圆顶的面积约是31400平方米。
【要点提示】掌握圆的面积公式是解题的关键。
23.78.5平方米
【解题思路】牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积。
【解答过程】
(平方米)
答:牛所能吃到草的最大面积是78.5平方米。
【要点提示】本题主要考查圆的面积公式。能理解牛最多可吃到草的面积就是以木桩为圆心,绳长为半径的圆的面积是解题的关键。
24.30厘米
【解题思路】此题的1.884米,是用来裱画的铝合金条的长度,实际就是一个圆形的周长,转化成已知周长求半径,利用周长公式计算即可。
【解答过程】1.884米=188.4厘米
188.4÷3.14÷2
=30(厘米)
答:这幅十字绣的半径是30厘米。
【要点提示】这题考查的是学生在复杂的条件中,提取出简单的量,把前面修饰的语言概括成已知周长求半径这一个简单的数学问题。此题还要注意把题目中的单位进行统一,熟记圆的周长公式。
25.5米
【解题思路】由圆的周长=πd,所以直径d=周长÷π。
【解答过程】15.7÷3.14=5(米)
答:直径是5米。
【要点提示】此题主要考查的是圆的周长公式的灵活应用。
26.244200元
【解答过程】试题分析:根据题意,组合图形的面积等于长方形的面积加上两个圆的的面积,其中长方形的宽即为圆的半径,可根据长方形的面积公式和圆的面积公式进行计算可得到组合图形的面积,然后再用组合图形的面积乘100元即可得到铺设该草坪需要的总钱数,列式解答即可得到答案.
解:(30×50+3.14×302××2)×100
=(1500+3.14×900××2)×100,
=(1500+942)×100,
=2442×100,
=244200(元);
答:街道铺设该草坪需要244200元的费用.
点评:解答此题的关键是根据长方形的面积公式和圆的面积公式确定组合图形的面积.
27.157平方厘米
【解题思路】从图中得知:此三角形为等腰直角三角形,所以把这3个扇形拼在一起,能得到半径为5厘米的半圆,由此得出这3个扇形的面积和是半径为5厘米的半圆的面积;所以利用圆的面积公式S=πr2进行解答。
【解答过程】把这3个扇形拼在一起,能得到半径为5厘米的半圆;
3.14×102÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
答:这3个扇形的面积和是157平方厘米。
【要点提示】关键是根据图得出这3个扇形的面积和是半径为5厘米的半圆的面积,再利用圆的面积公式解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
