【巩固复习】第二单元 圆柱和圆锥(培优卷.含解析)六年级下册数学苏教版
文档属性
| 名称 | 【巩固复习】第二单元 圆柱和圆锥(培优卷.含解析)六年级下册数学苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二单元 圆柱和圆锥
一、选择题
1.要求圆柱形烟囱用料多少就是求圆柱的( )。
A.表面积 B.侧面积 C.体积
2.把圆锥切一刀,切面不可能是( )。
A.三角形 B.椭圆形 C.平行四边形
3.一个圆锥的体积是18立方厘米,底面积是6平方厘米,高是( )厘米。
A.8 B.3 C.9 D.6
4.如图所示,绕3cm这条边旋转一周,得到的圆锥的体积是( )立方厘米。
A.50.24 B.37.68 C.150.72
5.一个圆柱的侧面积展开图是一个正方形,这个圆柱的底面周长与高的比是( )。
A.1∶4π B.1∶2 C.1∶1
6.如图,以长方形的边a作底面周长,边b作高分别可以围成一个长方体、正方体和圆柱体,再分别给它们配上两个底面。它们的体积相比,结果是( )。
A.长方体的体积最大 B.正方体的体积最大
C.圆柱体的体积最大 D.它们的体积一样大
7.下图中的正方体、圆柱和圆锥底面积相等,高也相等,下面( )是正确的。
A.正方体的体积是圆锥体积的3倍 B.圆柱的体积比正方体的体积大
C.圆柱的体积比正方体的体积小 D.圆锥的体积与正方体积相等
二、填空题
8.圆柱( )之间的距离叫作圆柱的高,圆锥( )到( )的距离是圆锥的高;圆柱有( )条高,圆锥有( )条高。
9.油漆圆柱形柱子,要计算油漆的面积有多大,就是求( )面积。
10.一根圆柱体的木料长6米。王明用了5分钟把它锯成了5段,表面积增加了20平方分米,这根木料的体积是( )立方分米。如果把它锯成8段要用( )分钟。
11.一个圆锥体积是5.024立方米,底面半径是4米,这个圆锥高 米.
12.一个圆锥和一个圆柱的底面积相等,体积比是1∶5,它们高的比是( )。
三、判断题
13.上、下两个底面都是圆的物体一定是圆柱。( )
14.圆柱的表面积是包裹在外面的部分,总比它的体积大。( )
15.将一张长40厘米、宽20厘米的长方形纸片卷成一个圆柱形纸筒,纸筒的侧面积是800平方厘米。( )
16.一个圆柱体水杯的底面直径是,高是(从里面测量得到的),则这个杯子可以装下一袋的豆奶。( )
17.一个圆锥的底面直径和高都是6dm,如果沿着底面直径纵切成两半,表面积增加12。( )
18.求圆柱木桶内盛多少升水,就是求木桶的容积。( )
19.一个正方体木料,加工成一个最大的圆锥,圆锥的体积是正方体体积的。( )
四、计算题
20.计算下面圆锥的体积。
21.计算下列圆柱的表面积与体积。(单位:厘米)
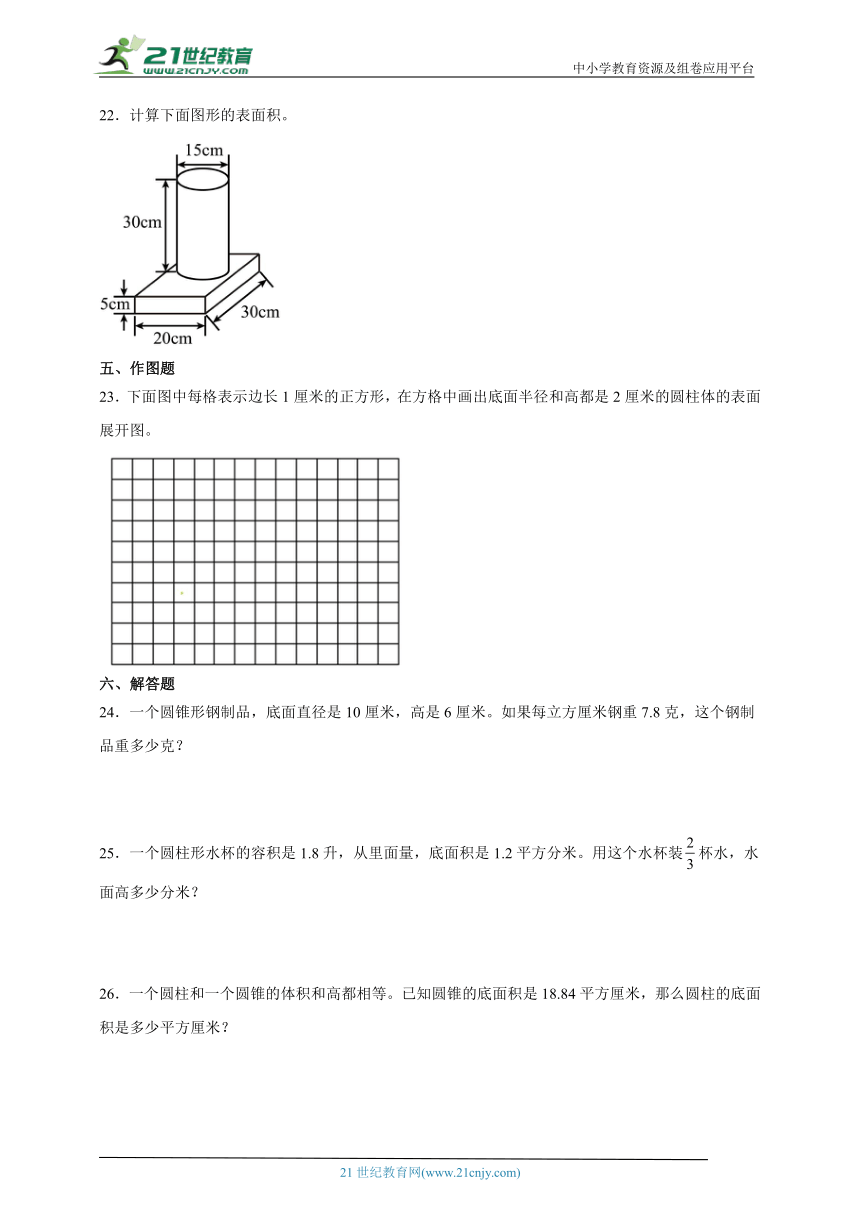
22.计算下面图形的表面积。
五、作图题
23.下面图中每格表示边长1厘米的正方形,在方格中画出底面半径和高都是2厘米的圆柱体的表面展开图。
六、解答题
24.一个圆锥形钢制品,底面直径是10厘米,高是6厘米。如果每立方厘米钢重7.8克,这个钢制品重多少克?
25.一个圆柱形水杯的容积是1.8升,从里面量,底面积是1.2平方分米。用这个水杯装杯水,水面高多少分米?
26.一个圆柱和一个圆锥的体积和高都相等。已知圆锥的底面积是18.84平方厘米,那么圆柱的底面积是多少平方厘米?
27.做一个底面直径是4分米,高是5分米的有盖圆柱形铁皮油桶。
(1)做这个铁皮油桶,至少要用铁皮多少平方分米?(得数保留整数)
(2)这个油桶里装了的油,这些油重多少千克?(每升油重0.82千克,得数保留整数)
28.一个圆柱形玻璃水槽,底面直径是20厘米,深是15厘米,用这个水槽装满水,再把这个水槽里的水全部倒入一个空的正方体金鱼缸中,已知金鱼缸从里面量的深是30厘米,问:金鱼缸中的水面高度大约是多少厘米?(最后得数保留整厘米)
29.张明买了一个圆柱形塑料笔筒,这个笔筒的高是1.5分米,底面周长是3.14分米。做这个笔筒至少需要塑料材料多少平方分米?
30.一根圆柱形木材长lOm,截成两根圆柱体后,表面积增加了1.2m2,原来这根木料的体积是多少立方米?
31.用一张长37.68cm、宽12.56cm的长方形纸围成一个圆柱形,有几种围法?计算一下,看哪一种围法体积大?
答案与解析
1.B
【解题思路】圆柱形烟囱只有侧面,没有底面,要求圆柱形烟囱用料多少就是求圆柱的侧面积。
【解答过程】通过分析,要求圆柱形烟囱用料多少就是求圆柱的侧面积。
故答案为:B
【要点提示】掌握圆柱的表面积、侧面积和体积的意义是解题的关键。
2.C
【解题思路】圆锥有一个圆形的底面和一个曲面,把圆锥切一刀,切面不可能是平行四边形。
【解答过程】把圆锥沿着顶点到底面直径切一刀,切面是三角形,沿着圆锥的一侧切一刀,切面是椭圆形,不可能是平行四边形。
故答案为:C
3.C
【解析】根据圆锥的体积公式:圆锥的体积=πr2h可得,圆锥的高=体积×3÷底面积,由此代入数据即可解答。
【解答过程】18×3÷6
=54÷6
=9(厘米)
故答案为:C
【要点提示】此题考查了圆锥的体积公式的应用。牢记公式是解题关键。
4.A
【解题思路】根据题意可知,圆锥的底面半径是4厘米,高是3厘米,圆锥的体积V= πr2h,代入数据计算即可。
【解答过程】×3.14×42×3
=3.14×16
=50.24(立方厘米)
故选择:A
【要点提示】此题考查圆锥的体积计算,牢记公式,找出圆锥的底面半径和高是解题关键。
5.C
【解题思路】由圆柱的侧面展开图的特点可知:圆柱的侧面沿高展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,再由“一个圆柱的侧面展开是一个正方形”可知,圆柱的高与底面周长相等,从而可以求出它们的比。
【解答过程】由题意可知:圆柱的高与底面周长相等,
则圆柱的底面周长∶高=1∶1
故答案为:C
【要点提示】本题考查了圆柱的展开图及比的意义,圆柱侧面沿高展开一般是长方形,当底面周长=高时,侧面沿高展开就是正方形。
6.C
【解题思路】围成的长方体、正方体和圆柱的高都是b,长方体、正方体和圆柱的体积V=Sh,高相等时,比较底面积,这三个图形哪个图形的底面积最大,对应图形的体积就最大。
【解答过程】围成的三个图形底面周长相等,周长相等时,圆的面积最大,所以圆柱的底面积最大。又因为围成的三个图形高相等,所以圆柱的体积最大。
故答案为:C
【要点提示】本题考查了长方体、正方体和圆柱的体积,熟记公式是解题的关键。
7.A
【解析】正方体和圆柱底面积相等,高也相等,那么体积必然相等;圆柱和圆锥底面积相等,高也相等,圆柱体积是圆锥的3倍,那么正方体的体积同样是圆锥的3倍。
【解答过程】
所以正方体和圆柱的体积相等,都是圆锥的3倍;
故答案选:A。
【要点提示】对于任何柱体,体积都可以用底面积乘高来计算,对于任何柱体,体积都是与其等底等高的柱体的。
8. 两个底面 顶点 底面圆心 无数 一
【解题思路】圆柱的上、下两个面都是圆形,两个底面面积大小相等,上下两个底面之间的距离叫作高;圆锥的底面是一个圆形,圆锥的侧面是曲面,从圆锥的顶点到底面圆心的距离是圆锥的高;
圆柱有无数条高,圆锥有一条高。
【解答过程】圆柱( 两个底面 )之间的距离叫作圆柱的高,圆锥( 顶点 )到( 底面圆心 )的距离是圆锥的高;圆柱有( 无数 )条高,圆锥有( 一 )条高。
【要点提示】该题考察圆柱和圆锥的定义和基本性质,属于基础知识,需熟练掌握。
9.侧
【解题思路】由于圆柱形柱子的上下底面不外露,所以求圆柱的侧面积,据此解答。
【解答过程】油漆圆柱形柱子,要计算油漆的面积有多大,就是求侧面积。
【要点提示】根据圆柱的表面积公式可知,表面积=侧面积+两个底面积,此题联系生活实际进行解答即可。
10. 150 8.75
【解题思路】锯成5段,增加了个面,用增加的面积除以增加的面数,即可求出一个面的面积,再乘圆柱的长,即可求出这根木料的体积,用了5分钟把它锯成了5段,可以理解为锯了4次,用时间除以次数,即可求出锯一次需要的时间,锯成8段,需要锯次,乘锯一次需要的时间,即可求出锯成8段要用的时间。
【解答过程】
(平方分米)
6米分米
(立方分米)
(分钟)
(分钟)
这根木料的体积是150立方分米。如果把它锯成8段要用8.75分钟。
11.0.3
【解答过程】试题分析:根据圆锥的体积公式,V=Sh,得出h=3V÷S,代入数据,即可解答.
解:5.024×3÷[3.14×42],
=15.072÷50.24,
=0.3(米);
答:这个圆锥的高是0.3米;
故答案为0.3.
点评:解答此题的关键是,将圆锥的体积公式进行变形,得出高的求法,代入数据,即可解答.
12.3∶5
【解析】设圆锥和圆柱的底面积都是1,设圆锥和圆柱的体积分别是1和5,然后求出各自的高,并计算圆锥和圆柱的高之比。
【解答过程】设圆锥和圆柱的底面积都是1,设圆锥和圆柱的体积分别是1和5;
圆柱:
5÷1=5
圆锥:
1×3÷1=3
所以圆锥和圆柱的高之比3∶5。
【要点提示】举例子是求解问题常用的方法,举例子的时候,尽可能举简单的、方便计算的例子。
13.×
【解题思路】因为圆柱每个横截面都是相等的,而不止是上下两个面相等,且圆柱的侧面展开是一个长方形,如:生活中我们认识的腰鼓,上下两个面都是相等的圆,但它不是圆柱体,所以一个物体,它的上下两个底面是相同的两个圆,它可能是圆柱体;据此判断。
【解答过程】一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体,此说法是错误的。
故答案为:×
【要点提示】此题考查了圆柱的特征,可通过举实例来推翻问题结论。
14.×
【解题思路】表面积和体积的比较是不成立的,两种不同的单位,不能进行比较。
【解答过程】表面积和体积是两种不同的单位,不能进行比较。圆柱的表面积是包裹在外面的部分,总比它的体积大,是错误的。
故答案为:×
【要点提示】此题考查的是对表面积和体积单位的概念区分。
15.√
【解题思路】根据题意,用一张长方形纸片卷成一个圆柱形纸筒,无论是以长方形的长作为圆柱的底面周长,宽作为圆柱的高;还是以长方形的宽作为圆柱的底面周长,长作为圆柱的高;根据可知,卷成的圆柱形纸筒的侧面积都等于长方形的面积,根据长方形面积=长×宽,即可求出纸筒的侧面积,据此判断。
【解答过程】40×20=800(平方厘米)
将一张长40厘米、宽20厘米的长方形纸片卷成一个圆柱形纸筒,纸筒的侧面积是800平方厘米。
原题说法正确。
故答案为:√
16.√
【解题思路】根据公式求出圆柱体的容积,再与498ml比较即可。
【解答过程】1立方厘米毫升。
(立方厘米)
502.4立方厘米毫升
502.4毫升毫升。
故答案为:√
【要点提示】本题主要考查的是圆柱体体积公式的应用。
17.×
【解题思路】沿着底面直径纵切成两半,增加了两个三角形,三角形的底和高都是6dm,据此列式计算。
【解答过程】表面积增加:
6×6÷2×2
=36÷2×2
=18×2
=36(平方分米)
故答案为:×
【要点提示】本题考查了立体图形的切拼,要熟悉圆锥的特征。
18.√
【解题思路】一个圆柱形木桶能盛水多少升,是指这个圆柱形木桶所能容纳水的体积,根据容积的意义:物体所能容纳物体的体积叫做物体的容积,据此解答。
【解答过程】根据分析可知,求圆柱木桶内盛多少升水,就是求木桶的容积。
原题干说法正确。
故答案为:√
【要点提示】解答本题的关键是弄清物体体积、容积的意义。
19.×
【解答过程】设正方体的棱长为a,则圆锥的高是a,圆锥的底面直径是a,底面半径是, 圆锥的体积是:×π×()2×a
=×π××a
=
正方体的体积是a×a×a=a3
圆锥的体积是正方体体积的:÷a3=, 原题说法错误。
故答案为:×
20.25.12cm3
【解题思路】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆锥的底面半径;再根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解答过程】12.56÷3.14÷2
=4÷2
=2(cm)
3.14×22×6×
=3.14×4×6×
=12.56×6×
=75.36×
=25.12(cm3)
圆锥的体积是25.12cm3。
21.533.8平方厘米;942立方厘米
【解题思路】由图可知,圆柱的直径为10厘米,则半径为5厘米,高为20厘米。根据圆柱的表面积公式:, 圆柱的体积公式:,代入数据即可解答。
【解答过程】3.14×(10÷2)2×2+3.14×10×12
=3.14×52×2+31.4×12
=3.14×25×2+376.8
=78.5×2+376.8
=157+376.8
=533.8(平方厘米)
3.14×(10÷2)2×12
=3.14×52×12
=3.14×25×12
=78.5×12
=942(立方厘米)
所以圆柱的表面积是533.8平方厘米,体积是942立方厘米。
22.3113cm2
【解题思路】观察图形可知,该图形的表面积等于长方体的表面积加上圆柱的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可。
【解答过程】(20×30+20×5+30×5)×2+3.14×15×30
=(600+100+150)×2+3.14×15×30
=850×2+3.14×15×30
=1700+1413
=1700+1413
=3113(cm2)
23.【解题思路】圆柱的展开图包含两个底面和一个侧面,其中底面是半径为2厘米的圆,侧面是长是半径是2厘米的圆的周长,宽是2厘米的长方形,据此画图。
【解答过程】长:2×2×3.14=12.56(厘米),宽:2厘米。
画图如下:
【要点提示】此题考查了圆柱的展开图,关键是明确侧面展开图与圆柱之间的关系。
24.1224.6克
【解题思路】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形钢制品的体积,再乘7.8,即可解答。
【解答过程】3.14×(10÷2)2×6××7.8
=3.14×52×6××7.8
=3.14×25×6××7.8
=78.5×6××7.8
=471××7.8
=157×7.8
=1224.6(克)
答:这个钢制品重1224.6克。
25.1分米
【解题思路】已知容积是1.8升,底面积是1.2平方分米,由圆柱体积公式变形,那么圆柱的高为1.8÷1.2=1.5(分米),因为装了杯水,则水面高为1.5×分米。据此解答即可。
【解答过程】1.8升=1.8立方分米
1.8÷1.2×
=1.5×
=1(分米)
答:水面高1分米。
26.6.28平方厘米
【解题思路】根据V柱=Sh,V锥=Sh可知,圆柱的底面积S柱=V÷h,圆锥的底面积S锥=3V÷h,所以当圆柱和圆锥等体积等高时,圆锥的底面积是圆柱底面积的3倍;用圆锥的底面积除以3,即是圆柱的底面积。
【解答过程】18.84÷3=6.28(平方厘米)
答:圆柱的底面积是6.28平方厘米。
27.(1)88平方分米
(2)41千克
【解题思路】(1)求所需要铁皮的平方米数,就是求圆柱的表面积。利用圆柱的表面积公式=2rh+2r,将数据代入即可;
(2)根据圆柱的体积公式=rh,求出圆柱的体积,再乘求出油的体积,再乘每升油的千克数,即可求出油的重量。
【解答过程】(1)2×3.14×(4÷2)×5+2×3.14×(4÷2)
=62.8+25.12
=87.92
88(平方分米)
答:做这个铁皮油桶,至少要用铁皮88平方分米。
(2)3.14×(4÷2)×5×
=3.14×4×5×
=50.24(立方分米)
=50.24(升)
50.24×0.82=41.196841(千克)
答:这些油重41千克。
【要点提示】本题主要考查属于圆柱的表面积和体积(容积)的实际应用,解答本题的关键是把问题转换为求圆柱的表面积与体积。
28.5厘米
【解题思路】根据圆柱的体积公式:底面积×高,代入数据,求出圆柱的体积;根据题意,已知金鱼缸从里面量深是30厘米,这个正方体的棱长是30厘米,根据正方体的体积公式:底面积×高,高=体积÷底面积,由于体积不变,用圆柱的体积除以正方体的底面积,即可求出金鱼缸的水面的高度。
【解答过程】3.14×(20÷2)2×15÷(30×30)
=3.14×102×15÷900
=3.14×100×15÷900
=314×15÷900
=4710÷900
≈5(厘米)
答:金鱼缸中的水面高度大约是5厘米。
【要点提示】本题考查圆柱的体积公式和正方体的体积公式的应用,关键是熟记公式,灵活运用。
29.5.495平方分米
【解题思路】需要多少材料就是求圆柱形塑料笔筒的表面积,因为笔筒的上底面没有,所以笔筒的表面积包括一个底面圆和一个侧面长方形。根据底面周长,求出底面半径,然后求出底面圆的面积,根据圆柱的表面积公式带入数据计算。
【解答过程】3.14×1.5=4.71(平方分米)
3.14÷3.14÷2=0.5(分米)
3.14×0.52=0.785(平方分米)
4.71+0.785=5.495(平方分米)
答:至少需要塑料材料5.495平方分米。
【要点提示】本题考查圆柱表面积的计算,熟记基本公式。易错点是笔筒的表面积只有一个底面和侧面。
30.6立方米
【解答过程】试题分析:将圆柱平行于底面截成2段,则表面积是增加了2个圆柱的底面积,由此即可求出圆柱的底面积是1.2÷2=0.6平方米,再利用圆柱的体积=底面积×高即可得解.
解:1.2÷2×10=6(立方米),
答:原来这根木材的体积是6立方米.
点评:抓住圆柱的切割特点,得出增加的表面积是2个圆柱的底面积,从而求出圆柱的底面积,是解决本题的关键.
31.有2种围法;当37.68厘米作为底面周长,12.56厘米作为高时圆柱体积最大,这个圆柱体的体积是1419.7824立方厘米
【解题思路】由题意知,圆柱的侧面展开后是一个长方形,有两种情况:①这个长方形的长跟圆柱的底面周长相等,是37.68厘米,宽跟圆柱的高相等,是12.56厘米;②这个长方形的宽跟圆柱的底面周长相等,是12.56厘米,宽跟圆柱的高相等,是37.68厘米;由此可利用公式V=Sh求得圆柱体的体积.
【解答过程】37.68÷3.14÷2=6(厘米)
3.14×62×12.56
=3.14×452.16
=1419.7824(立方厘米)
12.56÷3.14÷2=2(厘米)
3.14×22×37.68
=3.14×150.72
=473.2608(立方厘米)
答:有2种围法;当37.68厘米作为底面周长,12.56厘米作为高时圆柱体积最大,这个圆柱体的体积是1419.7824立方厘米.
【要点提示】此题考查了圆柱的体积计算,当题中没有直接告诉底面半径和高时要想办法先求得.注意分情况求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二单元 圆柱和圆锥
一、选择题
1.要求圆柱形烟囱用料多少就是求圆柱的( )。
A.表面积 B.侧面积 C.体积
2.把圆锥切一刀,切面不可能是( )。
A.三角形 B.椭圆形 C.平行四边形
3.一个圆锥的体积是18立方厘米,底面积是6平方厘米,高是( )厘米。
A.8 B.3 C.9 D.6
4.如图所示,绕3cm这条边旋转一周,得到的圆锥的体积是( )立方厘米。
A.50.24 B.37.68 C.150.72
5.一个圆柱的侧面积展开图是一个正方形,这个圆柱的底面周长与高的比是( )。
A.1∶4π B.1∶2 C.1∶1
6.如图,以长方形的边a作底面周长,边b作高分别可以围成一个长方体、正方体和圆柱体,再分别给它们配上两个底面。它们的体积相比,结果是( )。
A.长方体的体积最大 B.正方体的体积最大
C.圆柱体的体积最大 D.它们的体积一样大
7.下图中的正方体、圆柱和圆锥底面积相等,高也相等,下面( )是正确的。
A.正方体的体积是圆锥体积的3倍 B.圆柱的体积比正方体的体积大
C.圆柱的体积比正方体的体积小 D.圆锥的体积与正方体积相等
二、填空题
8.圆柱( )之间的距离叫作圆柱的高,圆锥( )到( )的距离是圆锥的高;圆柱有( )条高,圆锥有( )条高。
9.油漆圆柱形柱子,要计算油漆的面积有多大,就是求( )面积。
10.一根圆柱体的木料长6米。王明用了5分钟把它锯成了5段,表面积增加了20平方分米,这根木料的体积是( )立方分米。如果把它锯成8段要用( )分钟。
11.一个圆锥体积是5.024立方米,底面半径是4米,这个圆锥高 米.
12.一个圆锥和一个圆柱的底面积相等,体积比是1∶5,它们高的比是( )。
三、判断题
13.上、下两个底面都是圆的物体一定是圆柱。( )
14.圆柱的表面积是包裹在外面的部分,总比它的体积大。( )
15.将一张长40厘米、宽20厘米的长方形纸片卷成一个圆柱形纸筒,纸筒的侧面积是800平方厘米。( )
16.一个圆柱体水杯的底面直径是,高是(从里面测量得到的),则这个杯子可以装下一袋的豆奶。( )
17.一个圆锥的底面直径和高都是6dm,如果沿着底面直径纵切成两半,表面积增加12。( )
18.求圆柱木桶内盛多少升水,就是求木桶的容积。( )
19.一个正方体木料,加工成一个最大的圆锥,圆锥的体积是正方体体积的。( )
四、计算题
20.计算下面圆锥的体积。
21.计算下列圆柱的表面积与体积。(单位:厘米)
22.计算下面图形的表面积。
五、作图题
23.下面图中每格表示边长1厘米的正方形,在方格中画出底面半径和高都是2厘米的圆柱体的表面展开图。
六、解答题
24.一个圆锥形钢制品,底面直径是10厘米,高是6厘米。如果每立方厘米钢重7.8克,这个钢制品重多少克?
25.一个圆柱形水杯的容积是1.8升,从里面量,底面积是1.2平方分米。用这个水杯装杯水,水面高多少分米?
26.一个圆柱和一个圆锥的体积和高都相等。已知圆锥的底面积是18.84平方厘米,那么圆柱的底面积是多少平方厘米?
27.做一个底面直径是4分米,高是5分米的有盖圆柱形铁皮油桶。
(1)做这个铁皮油桶,至少要用铁皮多少平方分米?(得数保留整数)
(2)这个油桶里装了的油,这些油重多少千克?(每升油重0.82千克,得数保留整数)
28.一个圆柱形玻璃水槽,底面直径是20厘米,深是15厘米,用这个水槽装满水,再把这个水槽里的水全部倒入一个空的正方体金鱼缸中,已知金鱼缸从里面量的深是30厘米,问:金鱼缸中的水面高度大约是多少厘米?(最后得数保留整厘米)
29.张明买了一个圆柱形塑料笔筒,这个笔筒的高是1.5分米,底面周长是3.14分米。做这个笔筒至少需要塑料材料多少平方分米?
30.一根圆柱形木材长lOm,截成两根圆柱体后,表面积增加了1.2m2,原来这根木料的体积是多少立方米?
31.用一张长37.68cm、宽12.56cm的长方形纸围成一个圆柱形,有几种围法?计算一下,看哪一种围法体积大?
答案与解析
1.B
【解题思路】圆柱形烟囱只有侧面,没有底面,要求圆柱形烟囱用料多少就是求圆柱的侧面积。
【解答过程】通过分析,要求圆柱形烟囱用料多少就是求圆柱的侧面积。
故答案为:B
【要点提示】掌握圆柱的表面积、侧面积和体积的意义是解题的关键。
2.C
【解题思路】圆锥有一个圆形的底面和一个曲面,把圆锥切一刀,切面不可能是平行四边形。
【解答过程】把圆锥沿着顶点到底面直径切一刀,切面是三角形,沿着圆锥的一侧切一刀,切面是椭圆形,不可能是平行四边形。
故答案为:C
3.C
【解析】根据圆锥的体积公式:圆锥的体积=πr2h可得,圆锥的高=体积×3÷底面积,由此代入数据即可解答。
【解答过程】18×3÷6
=54÷6
=9(厘米)
故答案为:C
【要点提示】此题考查了圆锥的体积公式的应用。牢记公式是解题关键。
4.A
【解题思路】根据题意可知,圆锥的底面半径是4厘米,高是3厘米,圆锥的体积V= πr2h,代入数据计算即可。
【解答过程】×3.14×42×3
=3.14×16
=50.24(立方厘米)
故选择:A
【要点提示】此题考查圆锥的体积计算,牢记公式,找出圆锥的底面半径和高是解题关键。
5.C
【解题思路】由圆柱的侧面展开图的特点可知:圆柱的侧面沿高展开后,是一个长方形,长方形的长等于底面周长,宽等于圆柱的高,再由“一个圆柱的侧面展开是一个正方形”可知,圆柱的高与底面周长相等,从而可以求出它们的比。
【解答过程】由题意可知:圆柱的高与底面周长相等,
则圆柱的底面周长∶高=1∶1
故答案为:C
【要点提示】本题考查了圆柱的展开图及比的意义,圆柱侧面沿高展开一般是长方形,当底面周长=高时,侧面沿高展开就是正方形。
6.C
【解题思路】围成的长方体、正方体和圆柱的高都是b,长方体、正方体和圆柱的体积V=Sh,高相等时,比较底面积,这三个图形哪个图形的底面积最大,对应图形的体积就最大。
【解答过程】围成的三个图形底面周长相等,周长相等时,圆的面积最大,所以圆柱的底面积最大。又因为围成的三个图形高相等,所以圆柱的体积最大。
故答案为:C
【要点提示】本题考查了长方体、正方体和圆柱的体积,熟记公式是解题的关键。
7.A
【解析】正方体和圆柱底面积相等,高也相等,那么体积必然相等;圆柱和圆锥底面积相等,高也相等,圆柱体积是圆锥的3倍,那么正方体的体积同样是圆锥的3倍。
【解答过程】
所以正方体和圆柱的体积相等,都是圆锥的3倍;
故答案选:A。
【要点提示】对于任何柱体,体积都可以用底面积乘高来计算,对于任何柱体,体积都是与其等底等高的柱体的。
8. 两个底面 顶点 底面圆心 无数 一
【解题思路】圆柱的上、下两个面都是圆形,两个底面面积大小相等,上下两个底面之间的距离叫作高;圆锥的底面是一个圆形,圆锥的侧面是曲面,从圆锥的顶点到底面圆心的距离是圆锥的高;
圆柱有无数条高,圆锥有一条高。
【解答过程】圆柱( 两个底面 )之间的距离叫作圆柱的高,圆锥( 顶点 )到( 底面圆心 )的距离是圆锥的高;圆柱有( 无数 )条高,圆锥有( 一 )条高。
【要点提示】该题考察圆柱和圆锥的定义和基本性质,属于基础知识,需熟练掌握。
9.侧
【解题思路】由于圆柱形柱子的上下底面不外露,所以求圆柱的侧面积,据此解答。
【解答过程】油漆圆柱形柱子,要计算油漆的面积有多大,就是求侧面积。
【要点提示】根据圆柱的表面积公式可知,表面积=侧面积+两个底面积,此题联系生活实际进行解答即可。
10. 150 8.75
【解题思路】锯成5段,增加了个面,用增加的面积除以增加的面数,即可求出一个面的面积,再乘圆柱的长,即可求出这根木料的体积,用了5分钟把它锯成了5段,可以理解为锯了4次,用时间除以次数,即可求出锯一次需要的时间,锯成8段,需要锯次,乘锯一次需要的时间,即可求出锯成8段要用的时间。
【解答过程】
(平方分米)
6米分米
(立方分米)
(分钟)
(分钟)
这根木料的体积是150立方分米。如果把它锯成8段要用8.75分钟。
11.0.3
【解答过程】试题分析:根据圆锥的体积公式,V=Sh,得出h=3V÷S,代入数据,即可解答.
解:5.024×3÷[3.14×42],
=15.072÷50.24,
=0.3(米);
答:这个圆锥的高是0.3米;
故答案为0.3.
点评:解答此题的关键是,将圆锥的体积公式进行变形,得出高的求法,代入数据,即可解答.
12.3∶5
【解析】设圆锥和圆柱的底面积都是1,设圆锥和圆柱的体积分别是1和5,然后求出各自的高,并计算圆锥和圆柱的高之比。
【解答过程】设圆锥和圆柱的底面积都是1,设圆锥和圆柱的体积分别是1和5;
圆柱:
5÷1=5
圆锥:
1×3÷1=3
所以圆锥和圆柱的高之比3∶5。
【要点提示】举例子是求解问题常用的方法,举例子的时候,尽可能举简单的、方便计算的例子。
13.×
【解题思路】因为圆柱每个横截面都是相等的,而不止是上下两个面相等,且圆柱的侧面展开是一个长方形,如:生活中我们认识的腰鼓,上下两个面都是相等的圆,但它不是圆柱体,所以一个物体,它的上下两个底面是相同的两个圆,它可能是圆柱体;据此判断。
【解答过程】一个物体,它的上下两个底面是相同的两个圆,这个物体一定就是圆柱体,此说法是错误的。
故答案为:×
【要点提示】此题考查了圆柱的特征,可通过举实例来推翻问题结论。
14.×
【解题思路】表面积和体积的比较是不成立的,两种不同的单位,不能进行比较。
【解答过程】表面积和体积是两种不同的单位,不能进行比较。圆柱的表面积是包裹在外面的部分,总比它的体积大,是错误的。
故答案为:×
【要点提示】此题考查的是对表面积和体积单位的概念区分。
15.√
【解题思路】根据题意,用一张长方形纸片卷成一个圆柱形纸筒,无论是以长方形的长作为圆柱的底面周长,宽作为圆柱的高;还是以长方形的宽作为圆柱的底面周长,长作为圆柱的高;根据可知,卷成的圆柱形纸筒的侧面积都等于长方形的面积,根据长方形面积=长×宽,即可求出纸筒的侧面积,据此判断。
【解答过程】40×20=800(平方厘米)
将一张长40厘米、宽20厘米的长方形纸片卷成一个圆柱形纸筒,纸筒的侧面积是800平方厘米。
原题说法正确。
故答案为:√
16.√
【解题思路】根据公式求出圆柱体的容积,再与498ml比较即可。
【解答过程】1立方厘米毫升。
(立方厘米)
502.4立方厘米毫升
502.4毫升毫升。
故答案为:√
【要点提示】本题主要考查的是圆柱体体积公式的应用。
17.×
【解题思路】沿着底面直径纵切成两半,增加了两个三角形,三角形的底和高都是6dm,据此列式计算。
【解答过程】表面积增加:
6×6÷2×2
=36÷2×2
=18×2
=36(平方分米)
故答案为:×
【要点提示】本题考查了立体图形的切拼,要熟悉圆锥的特征。
18.√
【解题思路】一个圆柱形木桶能盛水多少升,是指这个圆柱形木桶所能容纳水的体积,根据容积的意义:物体所能容纳物体的体积叫做物体的容积,据此解答。
【解答过程】根据分析可知,求圆柱木桶内盛多少升水,就是求木桶的容积。
原题干说法正确。
故答案为:√
【要点提示】解答本题的关键是弄清物体体积、容积的意义。
19.×
【解答过程】设正方体的棱长为a,则圆锥的高是a,圆锥的底面直径是a,底面半径是, 圆锥的体积是:×π×()2×a
=×π××a
=
正方体的体积是a×a×a=a3
圆锥的体积是正方体体积的:÷a3=, 原题说法错误。
故答案为:×
20.25.12cm3
【解题思路】根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆锥的底面半径;再根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解答过程】12.56÷3.14÷2
=4÷2
=2(cm)
3.14×22×6×
=3.14×4×6×
=12.56×6×
=75.36×
=25.12(cm3)
圆锥的体积是25.12cm3。
21.533.8平方厘米;942立方厘米
【解题思路】由图可知,圆柱的直径为10厘米,则半径为5厘米,高为20厘米。根据圆柱的表面积公式:, 圆柱的体积公式:,代入数据即可解答。
【解答过程】3.14×(10÷2)2×2+3.14×10×12
=3.14×52×2+31.4×12
=3.14×25×2+376.8
=78.5×2+376.8
=157+376.8
=533.8(平方厘米)
3.14×(10÷2)2×12
=3.14×52×12
=3.14×25×12
=78.5×12
=942(立方厘米)
所以圆柱的表面积是533.8平方厘米,体积是942立方厘米。
22.3113cm2
【解题思路】观察图形可知,该图形的表面积等于长方体的表面积加上圆柱的侧面积,根据长方体的表面积公式:S=(ab+ah+bh)×2,圆柱的侧面积公式:S=πdh,据此代入数值进行计算即可。
【解答过程】(20×30+20×5+30×5)×2+3.14×15×30
=(600+100+150)×2+3.14×15×30
=850×2+3.14×15×30
=1700+1413
=1700+1413
=3113(cm2)
23.【解题思路】圆柱的展开图包含两个底面和一个侧面,其中底面是半径为2厘米的圆,侧面是长是半径是2厘米的圆的周长,宽是2厘米的长方形,据此画图。
【解答过程】长:2×2×3.14=12.56(厘米),宽:2厘米。
画图如下:
【要点提示】此题考查了圆柱的展开图,关键是明确侧面展开图与圆柱之间的关系。
24.1224.6克
【解题思路】根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形钢制品的体积,再乘7.8,即可解答。
【解答过程】3.14×(10÷2)2×6××7.8
=3.14×52×6××7.8
=3.14×25×6××7.8
=78.5×6××7.8
=471××7.8
=157×7.8
=1224.6(克)
答:这个钢制品重1224.6克。
25.1分米
【解题思路】已知容积是1.8升,底面积是1.2平方分米,由圆柱体积公式变形,那么圆柱的高为1.8÷1.2=1.5(分米),因为装了杯水,则水面高为1.5×分米。据此解答即可。
【解答过程】1.8升=1.8立方分米
1.8÷1.2×
=1.5×
=1(分米)
答:水面高1分米。
26.6.28平方厘米
【解题思路】根据V柱=Sh,V锥=Sh可知,圆柱的底面积S柱=V÷h,圆锥的底面积S锥=3V÷h,所以当圆柱和圆锥等体积等高时,圆锥的底面积是圆柱底面积的3倍;用圆锥的底面积除以3,即是圆柱的底面积。
【解答过程】18.84÷3=6.28(平方厘米)
答:圆柱的底面积是6.28平方厘米。
27.(1)88平方分米
(2)41千克
【解题思路】(1)求所需要铁皮的平方米数,就是求圆柱的表面积。利用圆柱的表面积公式=2rh+2r,将数据代入即可;
(2)根据圆柱的体积公式=rh,求出圆柱的体积,再乘求出油的体积,再乘每升油的千克数,即可求出油的重量。
【解答过程】(1)2×3.14×(4÷2)×5+2×3.14×(4÷2)
=62.8+25.12
=87.92
88(平方分米)
答:做这个铁皮油桶,至少要用铁皮88平方分米。
(2)3.14×(4÷2)×5×
=3.14×4×5×
=50.24(立方分米)
=50.24(升)
50.24×0.82=41.196841(千克)
答:这些油重41千克。
【要点提示】本题主要考查属于圆柱的表面积和体积(容积)的实际应用,解答本题的关键是把问题转换为求圆柱的表面积与体积。
28.5厘米
【解题思路】根据圆柱的体积公式:底面积×高,代入数据,求出圆柱的体积;根据题意,已知金鱼缸从里面量深是30厘米,这个正方体的棱长是30厘米,根据正方体的体积公式:底面积×高,高=体积÷底面积,由于体积不变,用圆柱的体积除以正方体的底面积,即可求出金鱼缸的水面的高度。
【解答过程】3.14×(20÷2)2×15÷(30×30)
=3.14×102×15÷900
=3.14×100×15÷900
=314×15÷900
=4710÷900
≈5(厘米)
答:金鱼缸中的水面高度大约是5厘米。
【要点提示】本题考查圆柱的体积公式和正方体的体积公式的应用,关键是熟记公式,灵活运用。
29.5.495平方分米
【解题思路】需要多少材料就是求圆柱形塑料笔筒的表面积,因为笔筒的上底面没有,所以笔筒的表面积包括一个底面圆和一个侧面长方形。根据底面周长,求出底面半径,然后求出底面圆的面积,根据圆柱的表面积公式带入数据计算。
【解答过程】3.14×1.5=4.71(平方分米)
3.14÷3.14÷2=0.5(分米)
3.14×0.52=0.785(平方分米)
4.71+0.785=5.495(平方分米)
答:至少需要塑料材料5.495平方分米。
【要点提示】本题考查圆柱表面积的计算,熟记基本公式。易错点是笔筒的表面积只有一个底面和侧面。
30.6立方米
【解答过程】试题分析:将圆柱平行于底面截成2段,则表面积是增加了2个圆柱的底面积,由此即可求出圆柱的底面积是1.2÷2=0.6平方米,再利用圆柱的体积=底面积×高即可得解.
解:1.2÷2×10=6(立方米),
答:原来这根木材的体积是6立方米.
点评:抓住圆柱的切割特点,得出增加的表面积是2个圆柱的底面积,从而求出圆柱的底面积,是解决本题的关键.
31.有2种围法;当37.68厘米作为底面周长,12.56厘米作为高时圆柱体积最大,这个圆柱体的体积是1419.7824立方厘米
【解题思路】由题意知,圆柱的侧面展开后是一个长方形,有两种情况:①这个长方形的长跟圆柱的底面周长相等,是37.68厘米,宽跟圆柱的高相等,是12.56厘米;②这个长方形的宽跟圆柱的底面周长相等,是12.56厘米,宽跟圆柱的高相等,是37.68厘米;由此可利用公式V=Sh求得圆柱体的体积.
【解答过程】37.68÷3.14÷2=6(厘米)
3.14×62×12.56
=3.14×452.16
=1419.7824(立方厘米)
12.56÷3.14÷2=2(厘米)
3.14×22×37.68
=3.14×150.72
=473.2608(立方厘米)
答:有2种围法;当37.68厘米作为底面周长,12.56厘米作为高时圆柱体积最大,这个圆柱体的体积是1419.7824立方厘米.
【要点提示】此题考查了圆柱的体积计算,当题中没有直接告诉底面半径和高时要想办法先求得.注意分情况求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
