浙江省宁波市慈溪市2024-2025学年下学期八年级期末数学试题(图片版,含答案)
文档属性
| 名称 | 浙江省宁波市慈溪市2024-2025学年下学期八年级期末数学试题(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 20:59:14 | ||
图片预览


文档简介
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
2024学年第二学期八年级期末测试卷
数学学科
参考答案及评分标准
一、选择题(本题共有 10题,每题 3分,满分 30分)
题号 1 2 3 *网] 4 5 6[来 7 8 9] 10
答案 B A B D C A D B C A
二、填空题(本题共有6题,每题3分,满分18分)
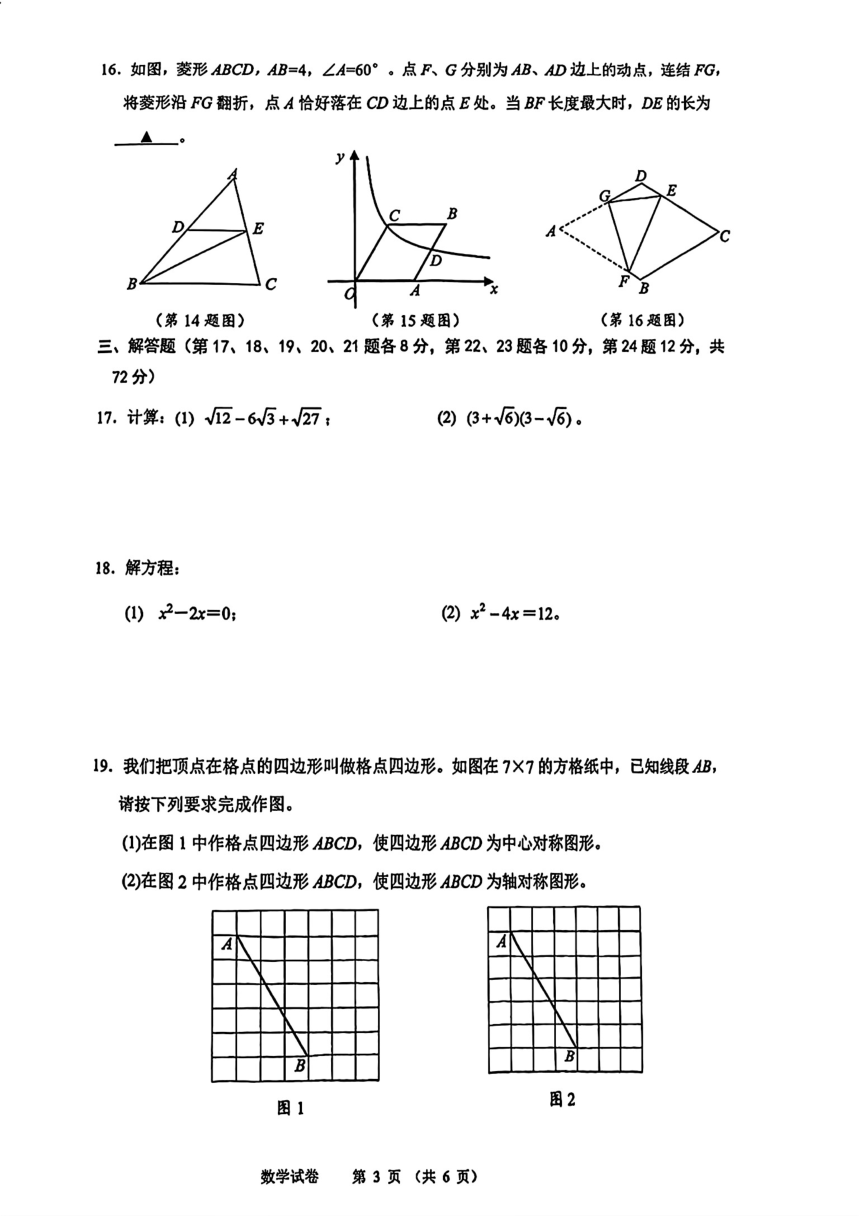
11. a 2 12.六 13.x 5 14.4 15.4 16.2 3 2
注:第 11题漏等号得 2分,第 13题只写 5得满分。
三、解答题(本大题共 8小题,共 72分。解答应写出文字说明、证明过程或演算步骤)
17.(1)原式= 2 3 6 3 3 3 2分
= 3。 4分
(2)原式=9-6 6分
=3。 8分
18.(1)x2-2x=0
x(x-2)=0 2分
∴方程的解为 x1=0,x2=2。 4分
(2)x2-4x=12
x 6 x 2 0 6分
∴方程的解为 x1=6,x2=-2 。 8分
19.答案不唯一
(1) (2) 8分
注:每图 4分,作法不唯一。
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
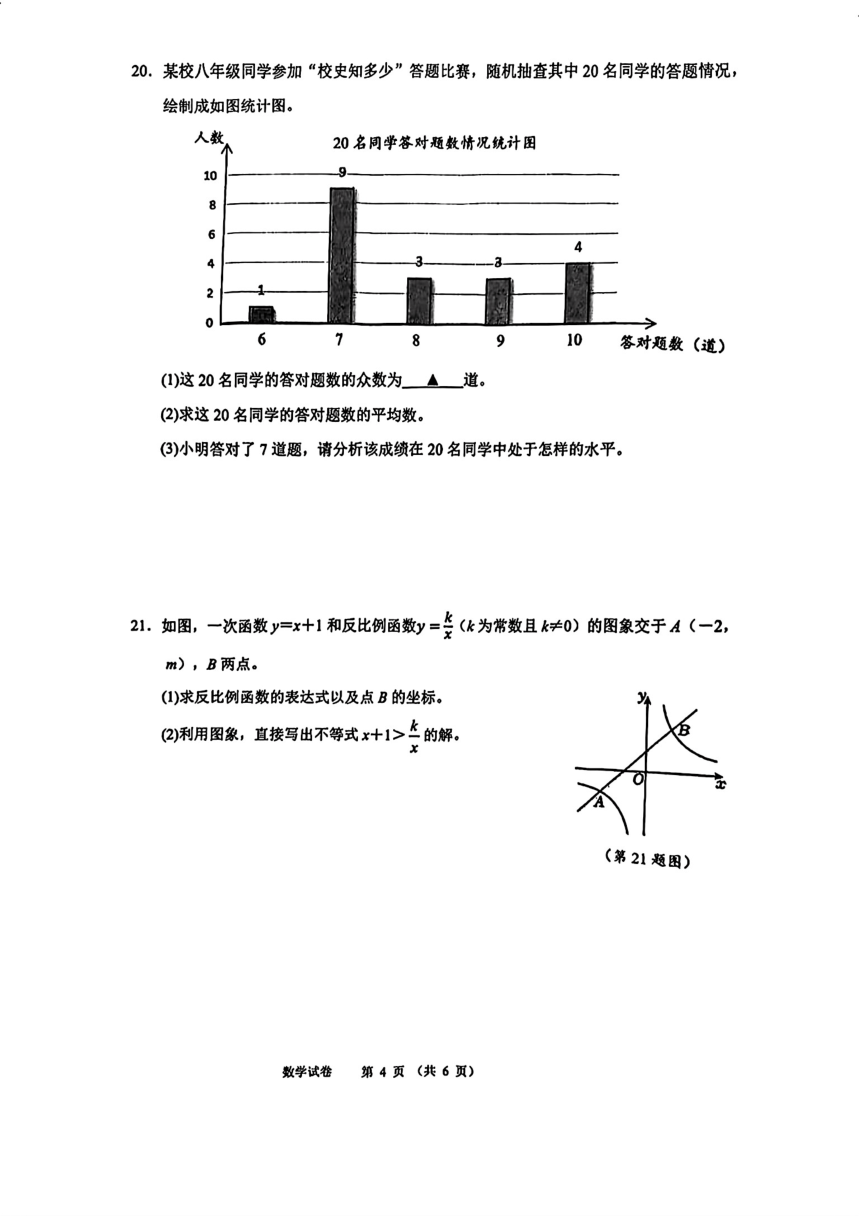
20.(1)7。 3分
2 x 1 6 9 7 3 8 3 9 4 10( )∵ 8道;
20
∴这 20名同学的答对题数的平均数为 8道。 6分
(3)平均数为 8道,中位数为 7.5道,所以小明的成绩略低于平均水平(合理即可)。
8分
21.(1)将点 A(-2,m)代入 y=x+1得,m=-2+1=-1,
∴点 A的坐标为(-2,-1), 2分
将 A(-2,-1)代入 = ,得 k=2
2
∴反比例函数的表达式为 y= 。 4分
∴点 B的坐标为(1,2) 5分
(2)-2<x<0或 x>1。 8分
注:第(2)小题其中 1个范围完全写对得 2分。
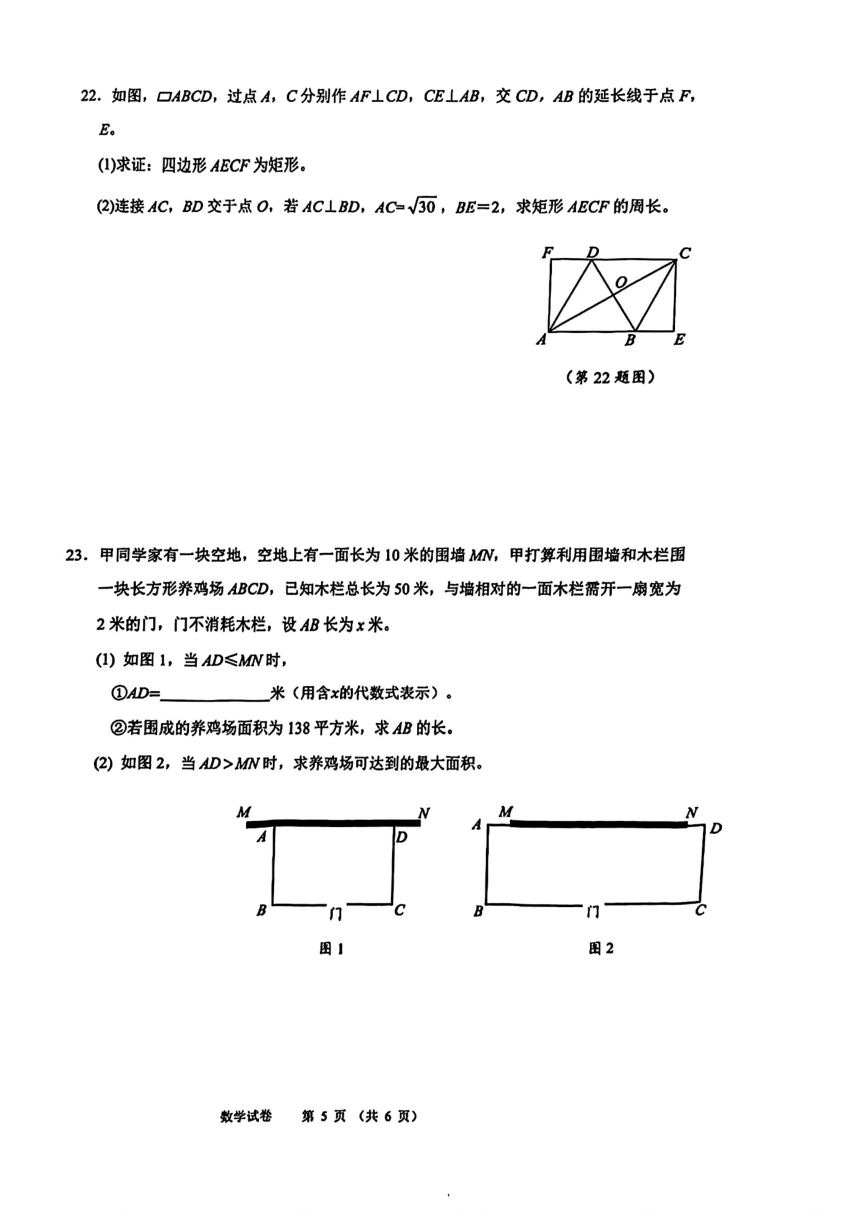
22.(1)证明:∵ABCD中,
∴CD∥AB,AD∥BC;
∵AF⊥CD,
∴AF⊥AB,
又∵CE⊥AB,
∴AF∥CE,
∴四边形 AECF是平行四边形。 3分
∴四边形 AECF是矩形。 5分
(2)∵四边形 ABCD是平行四边,AC⊥BD,
∴四边形 ABCD是菱形 , 6分
∴AB=BC。
设 AB=BC=x,
∵CE 2 AC 2 AE 2 CB2 BE 2,
2
∴ 30 x 2 2 x2 22, 8分
解得 x1 3, x2 5 (舍去)。
∴CE 5, 9分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
∴矩形 AECF的周长为 2 5 10。 10分
23. (1)①AD=52-2x 2分
②∵ x 52 2x 138, 4分
∴解得 x1 3, x2 23。 6分
∵52 2x 2 , 21 x 25
∴ AB的长为 23米。 7分
2 AD 50 12 2x( )∵ x 31,
2
31 2∴养鸡场 ABCD的面积 x 31 x x 961 。 9分
2 4
∵ x 31 10,
∴ x 21。
x 31 961∴当 时,养鸡场面积可以达到最大值 平方米。 10分
2 4
24(1)证明: ∵四边形 ABCD和四边形 CEFG均为正方形
∴CB=CD,CE=CG,∠BCD=∠ECG,
∴∠BCE=90° ∠ECD=∠DCG, 2分
∴△BCE≌△DCG(SAS),
∴DG=BE。 4分
(2)连结 CH,设 DG=x,DH=2x,
CE2 BE2 BC2∵ x2 16, EH 2 (4 x)2 (4 2x)2,
∴在 Rt△EHC中, HC 2 EH 2 EC 2 x2 16 (4 x)2 (4 2x)2。
∵在 Rt△HDC中,HC 2 HD2 DC 2 (2x)2 16,
∴16 (2x)2 x2 16 (4 x)2 (4 2x)2,
M
解得 x1 6 2 (5 舍去),x2 6 2 5,
∴BE= 6 2 5。 8分
9分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
(3)延长 CK,作 EP⊥CK于 P,作 DQ⊥CK于 Q,
易知 = ,∠ =∠ = 90°,
通过直角转换易得∠ =∠ ,
∠ =∠ = 90°
在△CEP和△GCN中, ∠ =∠ ,
=
∴△CEP≌△GCN(AAS)
∴ =
同理可证△CDQ≌△BCN,∴ = ,
∵ ⊥ , ⊥
∴ ∥
故以 E、P、D、Q为顶点的四边形是平行四边形
∴对角线 DE、PQ互相平分
即 K为 DE中点.
12分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
2024学年第二学期八年级期末测试卷
数学学科
参考答案及评分标准
一、选择题(本题共有 10题,每题 3分,满分 30分)
题号 1 2 3 *网] 4 5 6[来 7 8 9] 10
答案 B A B D C A D B C A
二、填空题(本题共有6题,每题3分,满分18分)
11. a 2 12.六 13.x 5 14.4 15.4 16.2 3 2
注:第 11题漏等号得 2分,第 13题只写 5得满分。
三、解答题(本大题共 8小题,共 72分。解答应写出文字说明、证明过程或演算步骤)
17.(1)原式= 2 3 6 3 3 3 2分
= 3。 4分
(2)原式=9-6 6分
=3。 8分
18.(1)x2-2x=0
x(x-2)=0 2分
∴方程的解为 x1=0,x2=2。 4分
(2)x2-4x=12
x 6 x 2 0 6分
∴方程的解为 x1=6,x2=-2 。 8分
19.答案不唯一
(1) (2) 8分
注:每图 4分,作法不唯一。
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
20.(1)7。 3分
2 x 1 6 9 7 3 8 3 9 4 10( )∵ 8道;
20
∴这 20名同学的答对题数的平均数为 8道。 6分
(3)平均数为 8道,中位数为 7.5道,所以小明的成绩略低于平均水平(合理即可)。
8分
21.(1)将点 A(-2,m)代入 y=x+1得,m=-2+1=-1,
∴点 A的坐标为(-2,-1), 2分
将 A(-2,-1)代入 = ,得 k=2
2
∴反比例函数的表达式为 y= 。 4分
∴点 B的坐标为(1,2) 5分
(2)-2<x<0或 x>1。 8分
注:第(2)小题其中 1个范围完全写对得 2分。
22.(1)证明:∵ABCD中,
∴CD∥AB,AD∥BC;
∵AF⊥CD,
∴AF⊥AB,
又∵CE⊥AB,
∴AF∥CE,
∴四边形 AECF是平行四边形。 3分
∴四边形 AECF是矩形。 5分
(2)∵四边形 ABCD是平行四边,AC⊥BD,
∴四边形 ABCD是菱形 , 6分
∴AB=BC。
设 AB=BC=x,
∵CE 2 AC 2 AE 2 CB2 BE 2,
2
∴ 30 x 2 2 x2 22, 8分
解得 x1 3, x2 5 (舍去)。
∴CE 5, 9分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
∴矩形 AECF的周长为 2 5 10。 10分
23. (1)①AD=52-2x 2分
②∵ x 52 2x 138, 4分
∴解得 x1 3, x2 23。 6分
∵52 2x 2 , 21 x 25
∴ AB的长为 23米。 7分
2 AD 50 12 2x( )∵ x 31,
2
31 2∴养鸡场 ABCD的面积 x 31 x x 961 。 9分
2 4
∵ x 31 10,
∴ x 21。
x 31 961∴当 时,养鸡场面积可以达到最大值 平方米。 10分
2 4
24(1)证明: ∵四边形 ABCD和四边形 CEFG均为正方形
∴CB=CD,CE=CG,∠BCD=∠ECG,
∴∠BCE=90° ∠ECD=∠DCG, 2分
∴△BCE≌△DCG(SAS),
∴DG=BE。 4分
(2)连结 CH,设 DG=x,DH=2x,
CE2 BE2 BC2∵ x2 16, EH 2 (4 x)2 (4 2x)2,
∴在 Rt△EHC中, HC 2 EH 2 EC 2 x2 16 (4 x)2 (4 2x)2。
∵在 Rt△HDC中,HC 2 HD2 DC 2 (2x)2 16,
∴16 (2x)2 x2 16 (4 x)2 (4 2x)2,
M
解得 x1 6 2 (5 舍去),x2 6 2 5,
∴BE= 6 2 5。 8分
9分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
(3)延长 CK,作 EP⊥CK于 P,作 DQ⊥CK于 Q,
易知 = ,∠ =∠ = 90°,
通过直角转换易得∠ =∠ ,
∠ =∠ = 90°
在△CEP和△GCN中, ∠ =∠ ,
=
∴△CEP≌△GCN(AAS)
∴ =
同理可证△CDQ≌△BCN,∴ = ,
∵ ⊥ , ⊥
∴ ∥
故以 E、P、D、Q为顶点的四边形是平行四边形
∴对角线 DE、PQ互相平分
即 K为 DE中点.
12分
{#{QQABaQSl4wAw0BQACI7aBUmeCAsQkJATLYomxRCYuAQiCBFABCA=}#}
同课章节目录
