2.3《二次根式》复习题--二次根式的加减法(含解析)八年级数学上册北师大版
文档属性
| 名称 | 2.3《二次根式》复习题--二次根式的加减法(含解析)八年级数学上册北师大版 |

|
|
| 格式 | docx | ||
| 文件大小 | 538.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 00:00:00 | ||
图片预览




文档简介
2.3《二次根式》复习题--二次根式的加减法
【题型1 最简二次根式的判断】
1.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
3.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4.下列各式中,属于最简二次根式的是( )
A. B. C. D.
【题型2 化为最简二次根式】
1.化简: .
2.将化成最简二次根式为 .
3.把化成最简二次根式的结果为 .
4.化简: ; : .
【题型3 已知最简二次根式求参数】
1.若与最简二次根式可以合并,则 .
2.若最简二次根式与可以合并,则的值为 .
3.若最简二次根式与最简二次根式相等,则 . .
4.若最简二次根式与可以合并,则 .
【题型4 同类二次根式的判断】
1.下列二次根式中,能与合并的是( )
A. B. C. D.
2.有下列二次根式:①、②、③、④,其中,与是同类二次根式的是( )
A.①③ B.②③ C.①④ D.③④
3.下列各组二次根式中,属于同类二次根式的是( ).
A.与 B.与 C.与 D.与
4.下列各组根式中,是同类二次根式的是( )
A.和 B.和
C.和 D.和
【题型5 求同类二次根式中的参数】
1.写出的两个同类二次根式为 .
2.已知与是同类二次根式,则的值可以是 (写两个即可).
3.若与最简二次根式是同类二次根式,则 .
4.如果最简二次根式和是同类二次根式,那么这两个二次根式的和为 .
【题型6 二次根式加减运算】
1.计算:
(1); (2).
2.计算:
(1) (2) (3)
3.计算:
(1) (2) (3) (4)
4.计算:
(1) (2) (3)
(4) (5); (6)
【题型7 二次根式的混合运算】
1.计算:
(1); (2).
2.计算:
(1); (2).
3.计算:
(1); (2).
4.计算:
(1); (2).
5.居民小区有块矩形绿地,绿地的长为米,宽为米.要在绿地内修建一个矩形小花坛(阴影部分),花坛的长为()米,宽为()米.
(1)求绿地的周长;(参考数值:,,结果精确到1米)
(2)除去修建花坛的地方,绿地的其余地方修建成通道.若通道要铺设造价为80元/米的地砖,铺设地砖需要花费多少元?
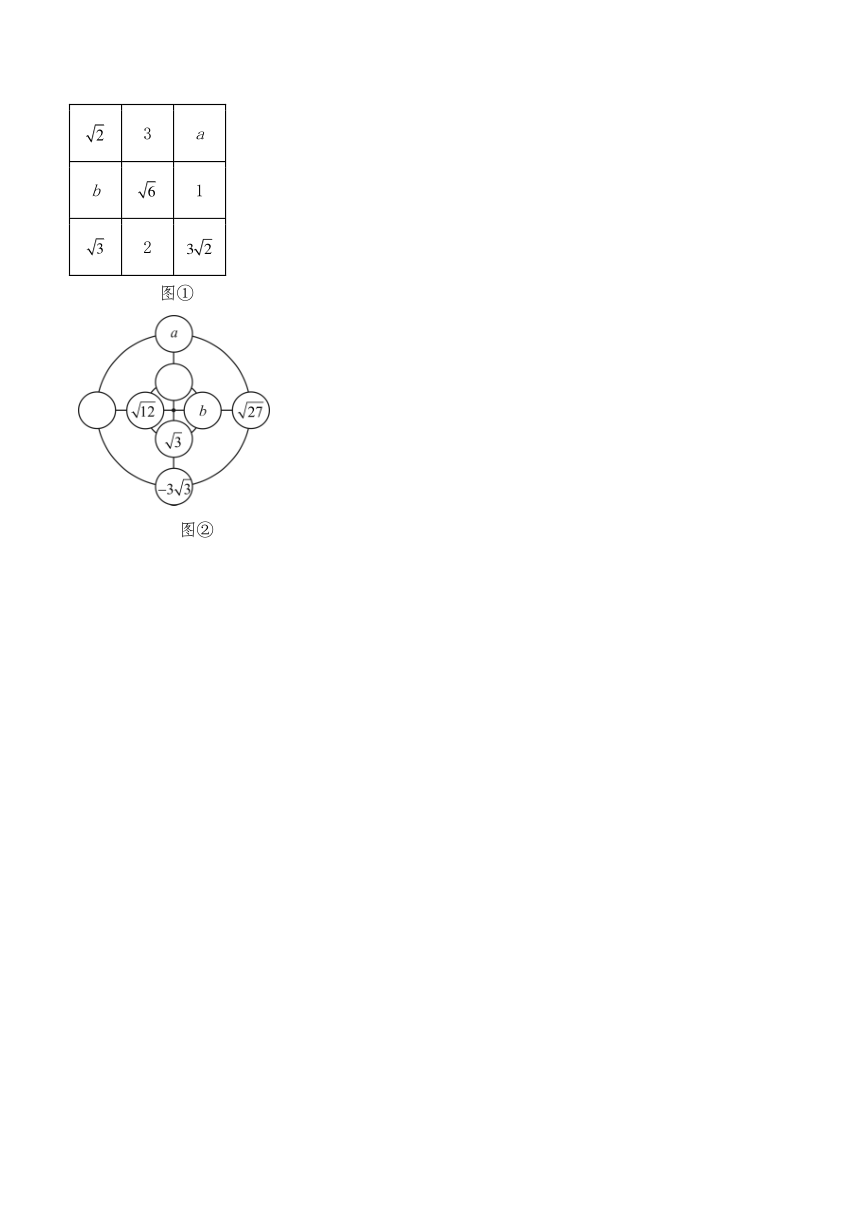
6.我国古代的《洛书》记载了世界上最早的幻方——“九宫格”.
(1)任务一:在图①方格中,若要使每一横、竖、斜对角的3个实数相乘都得到同样的结果,则__________,__________;
(2)任务二:在如图②的“幻圆”中,若内、外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,求的值.
3 a
b 1
2
图①
图②
参考答案
【题型1 最简二次根式的判断】
1.C
【知识点】最简二次根式的判断、化为最简二次根式
【分析】本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.
【详解】解:.,二次根式不是最简二次根式,故该选项不符合题意;
.,二次根式不是最简二次根式,故该选项不符合题意;
.是最简二次根式,故该选项符合题意;
.,二次根式不是最简二次根式,故该选项不符合题意;
故选:C.
2.A
【知识点】利用二次根式的性质化简、最简二次根式的判断
【分析】本题考查最简二次根式,熟练掌握相关的知识点是解题的关键.根据最简二次根式的定义进行判断即可.
【详解】解:A、是最简二次根式,符合题意;
B、,不是最简二次根式,不符合题意;
C、,不是最简二次根式,不符合题意;
D、,不是最简二次根式,不符合题意;
故选:A
3.B
【知识点】最简二次根式的判断
【分析】本题考查了最简二次根式的定义,掌握最简二次根式的定义是解题的关键.
根据最简二次根式的定义逐一判断即可.
【详解】解:A、,可以进行分母有理化,不是最简二次根式,故选项不符合题意;
B、,被开方数,不含能开得尽方的因数,是最简二次根式,故选项符合题意;
C、,可以进行分母有理化,不是最简二次根式,故选项不符合题意;
D、,含能开得尽方的因数4,不是最简二次根式,故选项不符合题意;
故选:B.
4.B
【知识点】最简二次根式的判断
【分析】本题考查了最简二次根式的定义.判定一个二次根式是不是最简二次根式的方法,就是逐个检查定义中的两个条件:①被开方数不含分母;②被开方数不含能开得尽方的因数或因式,据此即可判断.
【详解】解:A、,不是最简二次根式,故该选项不符合题意;
B、符合最简二次根式的条件,故本选项符合题意;
C、,不是最简二次根式,故本选项不符合题意;
D、,不是最简二次根式,故本选项不符合题意;
故答案为:B.
【题型2 化为最简二次根式】
1.
【知识点】利用二次根式的性质化简、化为最简二次根式
【分析】本题考查了利用二次根式的性质进行化简,根据二次根式的性质计算即可得解,熟练掌握二次根式的性质是解此题的关键.
【详解】解:,
故答案为:.
2.
【知识点】化为最简二次根式
【分析】本题考查的是最简二次根式,熟练运用二次根式的性质是解题的关键.直接利用二次根式性质化简即可.
【详解】解:,
故答案为:.
3.
【知识点】化为最简二次根式
【分析】本题考查了二次根式的性质,根据二次根式的性质进行化简即可.
【详解】解:,
故答案为:.
4. 7 /
【知识点】利用二次根式的性质化简、化为最简二次根式
【分析】本题主要考查的是二次根式的性质,熟练掌握二次根式的性质是解题的关键.依据二次根式的性质化简即可.
【详解】解:,,,
故答案为:,7,.
【题型3 已知最简二次根式求参数】
1.
【知识点】已知最简二次根式求参数
【分析】本题考查了同类二次根式及最简二次根式,根据题意得,进而可求解,熟练掌握基础知识是解题的关键.
【详解】解:依题意得:,
解得:,
故答案为:.
2.
【知识点】已知最简二次根式求参数、同类二次根式
【分析】此题考查了同类二次根式的定义及解一元一次方程等知识点,正确理解题意是解答本题的关键.
根据同类二次根式的定义得到,求解即可.
【详解】解:∵最简二次根式与可以合并,
∴与是同类二次根式,
∴,
解得,
故答案为.
3. 3 5
【知识点】已知最简二次根式求参数
【分析】本题考查最简二次根式的定义,同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.
根据题意可知,同类二次根式的被开方数相同,根指数相同,可得答案.
【详解】解:最简二次根式与最简二次根式相等,
∴,4n-m=2n+1
解得:,.
故答案为:3,5.
4.
【知识点】已知字母的值 ,求代数式的值、已知最简二次根式求参数、同类二次根式
【分析】根据最简二次根式与可以合并,判定二式是同类二次根式,得到,解答即可.
本题考查了最简二次根式,同类二次根式,求代数式的值,熟练掌握定义是解题的关键.
【详解】解:∵最简二次根式与可以合并
∴最简二次根式与是同类二次根式,
∴,
解得,
∴.
故答案为:.
【题型4 同类二次根式的判断】
1.B
【知识点】同类二次根式
【分析】本题考查了二次根式的加减,先把所给二次根式化简,再根据同类二次根式的定义判断即可,熟练掌握运算法则是解题的关键.
【详解】解:、与不能合并,原选项不符合题意;
、与能合并,原选项符合题意;
、与不能合并,原选项不符合题意;
、与不能合并,原选项不符合题意;
故选:.
2.C
【知识点】二次根式的除法、化为最简二次根式、同类二次根式
【分析】本题考查二次根式的化简、分母有理化、同类二次根式等知识.将题中四个数分别化成最简二次根式,再结合同类二次根式的定义解题即可.
【详解】解:①;②;③;④中,与是同类二次根式的是①④
故选:C.
3.A
【知识点】利用二次根式的性质化简、同类二次根式
【分析】本题主要考查了同类二次根式的定义,一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式,据此进行逐项分析,即可作答..
【详解】解:A、, 与是同类二次根式,故该选项符合题意;
B、,,与不是同类二次根式,故该选项不符合题意;
C、,,与不是同类二次根式,故该选项不符合题意;
D、,,与不是同类二次根式,故该选项不符合题意;
故选:A.
4.B
【知识点】同类二次根式
【分析】本题考查了同类二次根式,熟练掌握同类二次根式的定义是解题的关键.根据同类二次根式的定义,逐项分析即可判断.
【详解】A、,故和不是同类根式,不符合题意;
B、,故和是同类根式,符合题意;
C、,,故和不是同类根式,不符合题意;
D、和不是同类根式,不符合题意;
故选:B.
【题型5 求同类二次根式中的参数】
1.,(答案不唯一)
【知识点】利用二次根式的性质化简、同类二次根式
【分析】本题主要考查了同类二次根式的定义,熟练掌握一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式是解题的关键.
【详解】解:依题意,,
∴的两个同类二次根式为,.
故答案为:,(答案不唯一).
2.4或15
【知识点】同类二次根式、解一元一次方程(一)——合并同类项与移项
【分析】本题考查同类二次根式定义、解一元二次方程等知识,先由与是同类二次根式,得到,其中为实数,且,任意取两个值即可得到答案,熟记同类二次根式定义是解决问题的关键.
【详解】解:与是同类二次根式,
,其中为实数,且
当时,则,解得;
当时,则,解得;
......
的值可以是4或15(答案不唯一),
故答案为:4或15.
3.4
【知识点】同类二次根式
【分析】本题主要考查了同类二次根式,化简二次根式,熟知被开方数相同的最简二次根式是同类二次根式是解题的关键.先把化为最简二次根式,再根据同类二次根式的定义进行求解即可.
【详解】解:∵与最简二次根式是同类二次根式,
,
,
故答案为:4.
4.
【知识点】同类二次根式、二次根式的加减运算
【分析】本题考查了同类二次根式的知识,一元一次方程,注意掌握同类二次根式化为最简二次根式后被开方数相同且根指数均为2.根据同类二次根式的被开方数相同可得出关于的方程,解出的值,再求和即可.
【详解】解:∵最简二次根式和是同类二次根式,
∴,
解得:.
故这两个二次根式的和为,
故答案为:.
【题型6 二次根式加减运算】
1.(1)解:
;
(2)解:
.
2.(1)解:原式;
(2)解:原式;
(3)解:原式.
3.(1)解:原式;
(2)原式;
(3)原式;
(4)原式.
4.(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
;
(5)解:
;
(6)解:
.
【题型7 二次根式的混合运算】
1.(1)解:
;
(2)解:
2.(1)解:
;
(2)解:
.
3.(1)解:原式
;
(2)解:原式
.
4.(1)解:
;
(2)解:
;
5.(1)解:绿地的周长:
(米).
∴绿地的周长约为42米;
(2)解:
(平方米).
∴购买地砖的花费为(元).
6.解:(1)由题意可得:,
解得:,
,
解得:,
故答案为:,;
(2)设小圆与竖线相交的空白区域为,依题意得:
,
∴.
【题型1 最简二次根式的判断】
1.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
3.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
4.下列各式中,属于最简二次根式的是( )
A. B. C. D.
【题型2 化为最简二次根式】
1.化简: .
2.将化成最简二次根式为 .
3.把化成最简二次根式的结果为 .
4.化简: ; : .
【题型3 已知最简二次根式求参数】
1.若与最简二次根式可以合并,则 .
2.若最简二次根式与可以合并,则的值为 .
3.若最简二次根式与最简二次根式相等,则 . .
4.若最简二次根式与可以合并,则 .
【题型4 同类二次根式的判断】
1.下列二次根式中,能与合并的是( )
A. B. C. D.
2.有下列二次根式:①、②、③、④,其中,与是同类二次根式的是( )
A.①③ B.②③ C.①④ D.③④
3.下列各组二次根式中,属于同类二次根式的是( ).
A.与 B.与 C.与 D.与
4.下列各组根式中,是同类二次根式的是( )
A.和 B.和
C.和 D.和
【题型5 求同类二次根式中的参数】
1.写出的两个同类二次根式为 .
2.已知与是同类二次根式,则的值可以是 (写两个即可).
3.若与最简二次根式是同类二次根式,则 .
4.如果最简二次根式和是同类二次根式,那么这两个二次根式的和为 .
【题型6 二次根式加减运算】
1.计算:
(1); (2).
2.计算:
(1) (2) (3)
3.计算:
(1) (2) (3) (4)
4.计算:
(1) (2) (3)
(4) (5); (6)
【题型7 二次根式的混合运算】
1.计算:
(1); (2).
2.计算:
(1); (2).
3.计算:
(1); (2).
4.计算:
(1); (2).
5.居民小区有块矩形绿地,绿地的长为米,宽为米.要在绿地内修建一个矩形小花坛(阴影部分),花坛的长为()米,宽为()米.
(1)求绿地的周长;(参考数值:,,结果精确到1米)
(2)除去修建花坛的地方,绿地的其余地方修建成通道.若通道要铺设造价为80元/米的地砖,铺设地砖需要花费多少元?
6.我国古代的《洛书》记载了世界上最早的幻方——“九宫格”.
(1)任务一:在图①方格中,若要使每一横、竖、斜对角的3个实数相乘都得到同样的结果,则__________,__________;
(2)任务二:在如图②的“幻圆”中,若内、外两个圆周上四个数字之和以及外圆两直径上的四个数字之和都相等,求的值.
3 a
b 1
2
图①
图②
参考答案
【题型1 最简二次根式的判断】
1.C
【知识点】最简二次根式的判断、化为最简二次根式
【分析】本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.
【详解】解:.,二次根式不是最简二次根式,故该选项不符合题意;
.,二次根式不是最简二次根式,故该选项不符合题意;
.是最简二次根式,故该选项符合题意;
.,二次根式不是最简二次根式,故该选项不符合题意;
故选:C.
2.A
【知识点】利用二次根式的性质化简、最简二次根式的判断
【分析】本题考查最简二次根式,熟练掌握相关的知识点是解题的关键.根据最简二次根式的定义进行判断即可.
【详解】解:A、是最简二次根式,符合题意;
B、,不是最简二次根式,不符合题意;
C、,不是最简二次根式,不符合题意;
D、,不是最简二次根式,不符合题意;
故选:A
3.B
【知识点】最简二次根式的判断
【分析】本题考查了最简二次根式的定义,掌握最简二次根式的定义是解题的关键.
根据最简二次根式的定义逐一判断即可.
【详解】解:A、,可以进行分母有理化,不是最简二次根式,故选项不符合题意;
B、,被开方数,不含能开得尽方的因数,是最简二次根式,故选项符合题意;
C、,可以进行分母有理化,不是最简二次根式,故选项不符合题意;
D、,含能开得尽方的因数4,不是最简二次根式,故选项不符合题意;
故选:B.
4.B
【知识点】最简二次根式的判断
【分析】本题考查了最简二次根式的定义.判定一个二次根式是不是最简二次根式的方法,就是逐个检查定义中的两个条件:①被开方数不含分母;②被开方数不含能开得尽方的因数或因式,据此即可判断.
【详解】解:A、,不是最简二次根式,故该选项不符合题意;
B、符合最简二次根式的条件,故本选项符合题意;
C、,不是最简二次根式,故本选项不符合题意;
D、,不是最简二次根式,故本选项不符合题意;
故答案为:B.
【题型2 化为最简二次根式】
1.
【知识点】利用二次根式的性质化简、化为最简二次根式
【分析】本题考查了利用二次根式的性质进行化简,根据二次根式的性质计算即可得解,熟练掌握二次根式的性质是解此题的关键.
【详解】解:,
故答案为:.
2.
【知识点】化为最简二次根式
【分析】本题考查的是最简二次根式,熟练运用二次根式的性质是解题的关键.直接利用二次根式性质化简即可.
【详解】解:,
故答案为:.
3.
【知识点】化为最简二次根式
【分析】本题考查了二次根式的性质,根据二次根式的性质进行化简即可.
【详解】解:,
故答案为:.
4. 7 /
【知识点】利用二次根式的性质化简、化为最简二次根式
【分析】本题主要考查的是二次根式的性质,熟练掌握二次根式的性质是解题的关键.依据二次根式的性质化简即可.
【详解】解:,,,
故答案为:,7,.
【题型3 已知最简二次根式求参数】
1.
【知识点】已知最简二次根式求参数
【分析】本题考查了同类二次根式及最简二次根式,根据题意得,进而可求解,熟练掌握基础知识是解题的关键.
【详解】解:依题意得:,
解得:,
故答案为:.
2.
【知识点】已知最简二次根式求参数、同类二次根式
【分析】此题考查了同类二次根式的定义及解一元一次方程等知识点,正确理解题意是解答本题的关键.
根据同类二次根式的定义得到,求解即可.
【详解】解:∵最简二次根式与可以合并,
∴与是同类二次根式,
∴,
解得,
故答案为.
3. 3 5
【知识点】已知最简二次根式求参数
【分析】本题考查最简二次根式的定义,同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式称为同类二次根式.
根据题意可知,同类二次根式的被开方数相同,根指数相同,可得答案.
【详解】解:最简二次根式与最简二次根式相等,
∴,4n-m=2n+1
解得:,.
故答案为:3,5.
4.
【知识点】已知字母的值 ,求代数式的值、已知最简二次根式求参数、同类二次根式
【分析】根据最简二次根式与可以合并,判定二式是同类二次根式,得到,解答即可.
本题考查了最简二次根式,同类二次根式,求代数式的值,熟练掌握定义是解题的关键.
【详解】解:∵最简二次根式与可以合并
∴最简二次根式与是同类二次根式,
∴,
解得,
∴.
故答案为:.
【题型4 同类二次根式的判断】
1.B
【知识点】同类二次根式
【分析】本题考查了二次根式的加减,先把所给二次根式化简,再根据同类二次根式的定义判断即可,熟练掌握运算法则是解题的关键.
【详解】解:、与不能合并,原选项不符合题意;
、与能合并,原选项符合题意;
、与不能合并,原选项不符合题意;
、与不能合并,原选项不符合题意;
故选:.
2.C
【知识点】二次根式的除法、化为最简二次根式、同类二次根式
【分析】本题考查二次根式的化简、分母有理化、同类二次根式等知识.将题中四个数分别化成最简二次根式,再结合同类二次根式的定义解题即可.
【详解】解:①;②;③;④中,与是同类二次根式的是①④
故选:C.
3.A
【知识点】利用二次根式的性质化简、同类二次根式
【分析】本题主要考查了同类二次根式的定义,一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式,据此进行逐项分析,即可作答..
【详解】解:A、, 与是同类二次根式,故该选项符合题意;
B、,,与不是同类二次根式,故该选项不符合题意;
C、,,与不是同类二次根式,故该选项不符合题意;
D、,,与不是同类二次根式,故该选项不符合题意;
故选:A.
4.B
【知识点】同类二次根式
【分析】本题考查了同类二次根式,熟练掌握同类二次根式的定义是解题的关键.根据同类二次根式的定义,逐项分析即可判断.
【详解】A、,故和不是同类根式,不符合题意;
B、,故和是同类根式,符合题意;
C、,,故和不是同类根式,不符合题意;
D、和不是同类根式,不符合题意;
故选:B.
【题型5 求同类二次根式中的参数】
1.,(答案不唯一)
【知识点】利用二次根式的性质化简、同类二次根式
【分析】本题主要考查了同类二次根式的定义,熟练掌握一般地,把几个二次根式化为最简二次根式后,如果它们的被开方数相同,就把这几个二次根式叫做同类二次根式是解题的关键.
【详解】解:依题意,,
∴的两个同类二次根式为,.
故答案为:,(答案不唯一).
2.4或15
【知识点】同类二次根式、解一元一次方程(一)——合并同类项与移项
【分析】本题考查同类二次根式定义、解一元二次方程等知识,先由与是同类二次根式,得到,其中为实数,且,任意取两个值即可得到答案,熟记同类二次根式定义是解决问题的关键.
【详解】解:与是同类二次根式,
,其中为实数,且
当时,则,解得;
当时,则,解得;
......
的值可以是4或15(答案不唯一),
故答案为:4或15.
3.4
【知识点】同类二次根式
【分析】本题主要考查了同类二次根式,化简二次根式,熟知被开方数相同的最简二次根式是同类二次根式是解题的关键.先把化为最简二次根式,再根据同类二次根式的定义进行求解即可.
【详解】解:∵与最简二次根式是同类二次根式,
,
,
故答案为:4.
4.
【知识点】同类二次根式、二次根式的加减运算
【分析】本题考查了同类二次根式的知识,一元一次方程,注意掌握同类二次根式化为最简二次根式后被开方数相同且根指数均为2.根据同类二次根式的被开方数相同可得出关于的方程,解出的值,再求和即可.
【详解】解:∵最简二次根式和是同类二次根式,
∴,
解得:.
故这两个二次根式的和为,
故答案为:.
【题型6 二次根式加减运算】
1.(1)解:
;
(2)解:
.
2.(1)解:原式;
(2)解:原式;
(3)解:原式.
3.(1)解:原式;
(2)原式;
(3)原式;
(4)原式.
4.(1)解:
;
(2)解:
;
(3)解:
;
(4)解:
;
(5)解:
;
(6)解:
.
【题型7 二次根式的混合运算】
1.(1)解:
;
(2)解:
2.(1)解:
;
(2)解:
.
3.(1)解:原式
;
(2)解:原式
.
4.(1)解:
;
(2)解:
;
5.(1)解:绿地的周长:
(米).
∴绿地的周长约为42米;
(2)解:
(平方米).
∴购买地砖的花费为(元).
6.解:(1)由题意可得:,
解得:,
,
解得:,
故答案为:,;
(2)设小圆与竖线相交的空白区域为,依题意得:
,
∴.
同课章节目录
