【新课预习衔接】3.4向量在立体几何中的应用(培优卷.含解析)2025-2026学年高二上学期数学选择性必修第一册北师大版(2019)
文档属性
| 名称 | 【新课预习衔接】3.4向量在立体几何中的应用(培优卷.含解析)2025-2026学年高二上学期数学选择性必修第一册北师大版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 492.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 10:56:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 向量在立体几何中的应用
一.选择题(共5小题)
1.(2024 金东区校级模拟)已知矩形ABCD,AB=1,BC,沿对角线AC将△ABC折起,若平面ABC与平面ACD所成角的余弦值为,则B与D之间距离为( )
A.1 B. C. D.
2.(2024 福州期末)如图,ABCD﹣EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到直线AB的距离为( )
A. B. C. D.
3.(2024 肇东市校级期末)已知A(1,0,1),是平面α的一个法向量,且B(﹣1,2,2)是平面α内一点,则点A到平面α的距离为( )
A. B. C. D.
4.(2024 辽阳期末)在平面四边形ABCD中,△ABC为正三角形,AD⊥CD,AD=CD,如图1,将四边形沿AC折起,得到如图2所示的四面体B﹣ACD,若四面体B﹣ACD外接球的球心为O,当四面体B﹣ACD的体积最大时,点O到平面ABD的距离为( )
A. B. C. D.
5.(2024秋 吕梁月考)若平面α的法向量(1,2,﹣3),直线l的方向向量(1,1,1),则( )
A.l∥α B.l⊥α C.l α D.l∥α或l α
二.多选题(共2小题)
(多选)6.(2024 博爱县校级期末)若平面α,β的法向量分别是,,直线l的方向向量为,直线m的方向向量为,则( )
A.α⊥β
B.l∥α
C.l与m为相交直线
D.在上的投影向量为
(多选)7.(2024 南岸区模拟)如图,在正三棱柱ABC﹣A1B1C1中,P为空间一动点,若,则( )
A.若λ=μ,则点P的轨迹为线段BC1
B.若λ+μ=1,则点P的轨迹为线段B1C
C.存在λ,μ∈(0,1),使得AP⊥BC
D.存在λ,μ∈(0,1),使得AP∥平面A1B1C1
三.填空题(共3小题)
8.(2024 徐汇区校级期末)直线m与平面α所成角为60°,则m与平面α内任意直线所成角的取值范围是 .
9.(2024 博白县模拟)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到库底与水坝的交线AB的距离分别为m,CB=5m.又测得AB的长为5m,CD的长为m,则水库底面与水坝斜面所成的二面角的大小为 .
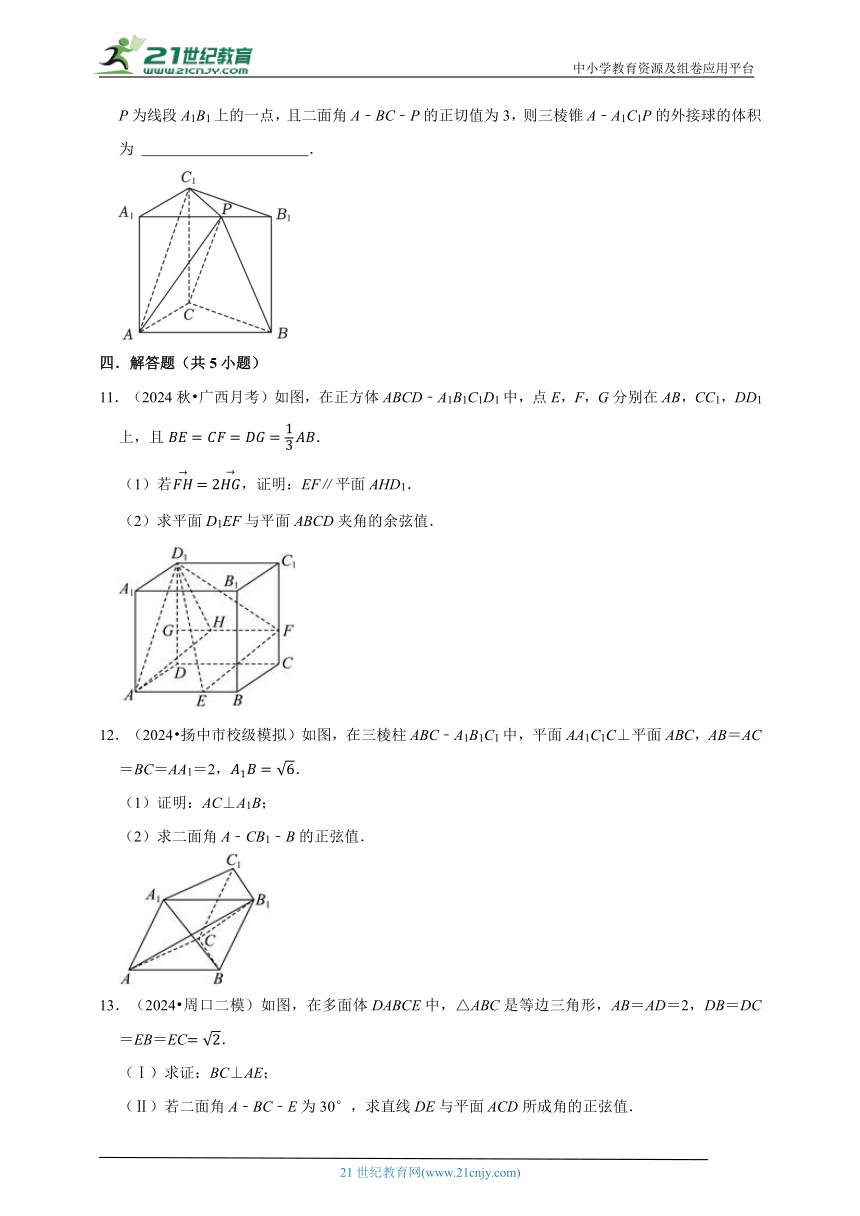
10.(2024 洪山区校级模拟)如图,在直三棱柱ABC﹣A1B1C1中,AA1=3,BC=6,,P为线段A1B1上的一点,且二面角A﹣BC﹣P的正切值为3,则三棱锥A﹣A1C1P的外接球的体积为 .
四.解答题(共5小题)
11.(2024秋 广西月考)如图,在正方体ABCD﹣A1B1C1D1中,点E,F,G分别在AB,CC1,DD1上,且.
(1)若,证明:EF∥平面AHD1.
(2)求平面D1EF与平面ABCD夹角的余弦值.
12.(2024 扬中市校级模拟)如图,在三棱柱ABC﹣A1B1C1中,平面AA1C1C⊥平面ABC,AB=AC=BC=AA1=2,.
(1)证明:AC⊥A1B;
(2)求二面角A﹣CB1﹣B的正弦值.
13.(2024 周口二模)如图,在多面体DABCE中,△ABC是等边三角形,AB=AD=2,DB=DC=EB=EC.
(Ⅰ)求证:BC⊥AE;
(Ⅱ)若二面角A﹣BC﹣E为30°,求直线DE与平面ACD所成角的正弦值.
14.(2024 山西模拟)如图,已知平行六面体ABCD﹣A1B1C1D1的所有棱长均相等,AD⊥平面ABB1A1,P为D1C1的中点,且PD=PC.
(1)求证:CC1⊥BD;
(2)求平面CPB与平面DPB的夹角的正弦值.
15.(2024 保定三模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,AC与BD相交于点E,点F在PC上,.
(1)证明:DF⊥平面PBC;
(2)若PA与平面BDF所成的角为α,平面PAD与平面PBC的夹角为β,求α+β.
新课预习衔接 向量在立体几何中的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024 金东区校级模拟)已知矩形ABCD,AB=1,BC,沿对角线AC将△ABC折起,若平面ABC与平面ACD所成角的余弦值为,则B与D之间距离为( )
A.1 B. C. D.
【考点】空间向量法求解二面角及两平面的夹角.
【专题】转化思想;向量法;转化法;空间位置关系与距离;数学运算.
【答案】C
【分析】过B和D分别作BE⊥AC,DF⊥AC,根据向量垂直的性质,利用向量数量积进行转化求解即可.
【解答】解:过B和D分别作BE⊥AC,DF⊥AC,
∵AB=1,BC,
∴AC=2,
∵AB BCAC BE,
∴BE=DF,
则AE=CF,即EF=2﹣1=1,
∵平面ABC与平面ACD所成角的余弦值为,
∴cos,,
∵,
∴2=()2222+2 2 2 12|| ||cos,2()3,
则||,
即B与D之间距离为,
故选:C.
【点评】本题主要考查空间两点间距离的计算,利用向量数量积与长度之间的关系进行转化求解是解决本题的关键,是中档题.
2.(2024 福州期末)如图,ABCD﹣EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到直线AB的距离为( )
A. B. C. D.
【考点】空间中点到直线的距离及两平行直线间的距离.
【专题】计算题;转化思想;综合法;空间位置关系与距离;逻辑推理;直观想象;数学运算.
【答案】C
【分析】建立空间直角坐标系,表示出,,进而得到在上的投影向量的长度,即可求出答案.
【解答】解:建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),D(0,1,0),E(0,0,1),
所以(1,0,0),(0,1,0),(0,0,1),
则(1,0,0)(0,1,0)(0,0,1)=(,,),
因为(1,0,0),
所以在上的投影向量的长度为:,
所以点P到AB的距离,
故选:C.
【点评】本题考查点到直线的距离,利用空间直角坐标系是关键,属于中档题.
3.(2024 肇东市校级期末)已知A(1,0,1),是平面α的一个法向量,且B(﹣1,2,2)是平面α内一点,则点A到平面α的距离为( )
A. B. C. D.
【考点】空间中点到平面的距离.
【专题】转化思想;向量法;空间向量及应用;数学运算.
【答案】D
【分析】求出的坐标,再利用点到面的距离公式求解即可.
【解答】解:由已知,又是平面α的一个法向量,
则点A到平面α的距离为.
故选:D.
【点评】本题考查利用向量法求解点到平面的距离,属基础题.
4.(2024 辽阳期末)在平面四边形ABCD中,△ABC为正三角形,AD⊥CD,AD=CD,如图1,将四边形沿AC折起,得到如图2所示的四面体B﹣ACD,若四面体B﹣ACD外接球的球心为O,当四面体B﹣ACD的体积最大时,点O到平面ABD的距离为( )
A. B. C. D.
【考点】空间中点到平面的距离.
【专题】转化思想;综合法;立体几何;数学运算.
【答案】C
【分析】根据题意可得当平面ABC⊥平面ACD时,四面体B﹣ACD的体积最大,在平面ABC内过B作BE⊥AC于点E,则BE⊥平面ACD,再建系,利用向量法,向量数量积运算,即可求解.
【解答】解:根据题意可得当平面ABC⊥平面ACD时,四面体B﹣ACD的体积最大,
在平面ABC内过B作BE⊥AC于点E,则BE⊥平面ACD,
∵△ABC为正三角形,AD⊥CD,易知AC⊥ED,
∴四面体B﹣ACD外接球的球心O为正三角形ABC的中心,即BH的靠近E的三等分点,
建系如图,则根据题意可得:
A(1,0,0),B(0,0,),D(0,1,0),O(0,0,),
∴,,,
设平面ABD的法向量为,
则,取,
∴点O到平面ABD的距离为.
故选:C.
【点评】本题考查向量法求解点面距问题,属中档题.
5.(2024秋 吕梁月考)若平面α的法向量(1,2,﹣3),直线l的方向向量(1,1,1),则( )
A.l∥α B.l⊥α C.l α D.l∥α或l α
【考点】平面的法向量;空间向量的数量积判断向量的共线与垂直;空间直线的方向向量、空间直线的向量参数方程.
【专题】计算题;转化思想;向量法;空间位置关系与距离;数学运算.
【答案】D
【分析】根据法向量与方向向量数量积的运算结果,结合线面关系进行判断即可.
【解答】解:因为,
所以l∥α或l α.
故选:D.
【点评】本题考查了利用向量法判断直线与平面的位置关系,属于基础题.
二.多选题(共2小题)
(多选)6.(2024 博爱县校级期末)若平面α,β的法向量分别是,,直线l的方向向量为,直线m的方向向量为,则( )
A.α⊥β
B.l∥α
C.l与m为相交直线
D.在上的投影向量为
【考点】空间向量语言表述线面的垂直、平行关系;空间向量语言表述面面的垂直、平行关系;空间向量的数量积判断向量的共线与垂直;空间直线的方向向量、空间直线的向量参数方程;平面的法向量.
【专题】计算题;方程思想;转化思想;综合法;空间向量及应用;数学运算.
【答案】AD
【分析】根据题意,由平面与平面垂直的判断方法分析A,由直线与平面的位置关系分析B,由向量平行的方法分析C,由投影向量公式分析D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,平面α,β的法向量分别是,,
由于,则有α⊥β,故A正确;
对于B,,则l∥α或l α,故B错误;
对于C,设,,此方程组无解,则l与为相交直线或异面直线,故C错误;
对于D,在上的投影向量为,故D正确.
故选:AD.
【点评】本题考查空间向量的应用,涉及直线与平面平行、垂直的判断方法,属于基础题.
(多选)7.(2024 南岸区模拟)如图,在正三棱柱ABC﹣A1B1C1中,P为空间一动点,若,则( )
A.若λ=μ,则点P的轨迹为线段BC1
B.若λ+μ=1,则点P的轨迹为线段B1C
C.存在λ,μ∈(0,1),使得AP⊥BC
D.存在λ,μ∈(0,1),使得AP∥平面A1B1C1
【考点】空间向量方法证明线、面的位置关系定理;棱柱的结构特征.
【专题】计算题;方程思想;转化思想;综合法;立体几何;数学抽象.
【答案】ABC
【分析】根据题意,由平面向量基本定理分析A、B、C,由直线与平面平行的性质分析D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,由平面向量基本定理,若,则点P在侧面BCC1B1内(含边界),
又由λ=μ,则,而λ∈[0,1],故点P的轨迹为线段BC1,故A正确;
对于B,若λ+μ=1,则,所以,即,则P在直线B1C上,
又λ∈[0,1],故点P的轨迹为线段B1C,故B正确;
对于C,分别取棱BC,B1C1的中点D,E,连接DE,由于BC⊥AD且BC⊥DE,则BC⊥平面ADEA1,
当点P在线段DE上时,AP⊥BC,故存在λ,μ∈(0,1),使得AP⊥BC,故C正确;
对于D,由直线与平面平行的性质,若AP∥平面A1B1C1,则点P必在棱BC上,此时μ=0,
故不存在λ,μ∈(0,1),使得AP∥平面A1B1C1,故D错误.
故选:ABC.
【点评】本题考查棱柱的结构特征,涉及向量的线性运算,属于中档题.
三.填空题(共3小题)
8.(2024 徐汇区校级期末)直线m与平面α所成角为60°,则m与平面α内任意直线所成角的取值范围是 [,] .
【考点】直线与平面所成的角;异面直线及其所成的角.
【专题】转化思想;综合法;空间角;数学运算.
【答案】[,].
【分析】直线与平面所成的角是直线与平面内任意一条直线所成角中最小的角,结合直线与平面所成角的范围为00≤θ即可得.
【解答】解:直线与平面所成的角是直线与平面内任意一条直线所成角中最小的角,
且直线与平面所成角的范围为0≤θ,
则m与平面α内任意直线所成角的取值范围是[,].
故答案为:[,].
【点评】本题考查直线与平面所成角与异面直线所成角,属于中档题.
9.(2024 博白县模拟)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到库底与水坝的交线AB的距离分别为m,CB=5m.又测得AB的长为5m,CD的长为m,则水库底面与水坝斜面所成的二面角的大小为 .
【考点】二面角的平面角及求法.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】.
【分析】作BE∥AD且BE=AD,连接DE,可得∠CBE是所求二面角的平面角,进而求得BE,CE,再利用余弦定理可求得cos∠CBE,可求得∠CBE.
【解答】解:如图,作BE∥AD且BE=AD,连接DE,又AD⊥AB,则四边形ABED是矩形,
BE⊥AB.又BC⊥AB,所以∠CBE是所求二面角的平面角,
因为DE∥AB,BC⊥AB,则BC⊥DE,
又BE⊥DE,BC∩BE=B,BC,BE 平面BCE,
所以DE⊥平面BCE,而CE 平面BCE,
所以DE⊥CE,DE=AB=5,
所以,,
由题可知BC=5,
则,
又∠CBE是三角形的内角,
所以.
故答案为:.
【点评】本题考查二面角的计算,属于中档题.
10.(2024 洪山区校级模拟)如图,在直三棱柱ABC﹣A1B1C1中,AA1=3,BC=6,,P为线段A1B1上的一点,且二面角A﹣BC﹣P的正切值为3,则三棱锥A﹣A1C1P的外接球的体积为 .
【考点】二面角的平面角及求法;球的体积和表面积.
【专题】计算题;转化思想;综合法;空间位置关系与距离;空间角;直观想象;数学运算.
【答案】.
【分析】根据题意,由条件可得∠PNM是二面角A﹣BC﹣P的平面角,再将三棱锥A﹣A1C1P补为长方体,则长方体的外接球即为三棱锥的外接球,再由球的体积公式,即可得到结果.
【解答】解:如图,作PM∥AA1,交AB于M,则PM=AA1=3,
过M作MN⊥BC交BC于点N,连接PN.
因为ABC﹣A1B1C1为直三棱柱,则AA1⊥平面ABC,且PM∥AA1,
则PM⊥平面ABC,且BC 平面ABC,所以PM⊥BC,
又MN⊥BC,PM∩MN=M,PM,MN 平面PMN,
所以BC⊥平面PMN,PN 平面PMN,所以PN⊥BC,
则∠PNM是二面角A﹣BC﹣P的平面角,
所以,所以MN=1,
又,BC=6,所以,所以,.
可把三棱锥A﹣A1C1P补成棱长为,,3的长方体,
则三棱锥A﹣A1C1P的外接球的半径为,
所以三棱锥A﹣A1C1P的外接球的体积为.
故答案为:.
【点评】本题考查球的体积计算问题,涉及二面角的求法,是中档题.
四.解答题(共5小题)
11.(2024秋 广西月考)如图,在正方体ABCD﹣A1B1C1D1中,点E,F,G分别在AB,CC1,DD1上,且.
(1)若,证明:EF∥平面AHD1.
(2)求平面D1EF与平面ABCD夹角的余弦值.
【考点】空间向量法求解二面角及两平面的夹角;直线与平面平行.
【专题】转化思想;向量法;空间角;数学运算.
【答案】(1)证明过程请见解答;(2).
【分析】(1)先证明四边形HFEA为平行四边形,可得EF∥AH,再由线面平行的判定定理,即可得证;
(2)以D为坐标原点建立空间直角坐标系,利用向量法求平面与平面的夹角,即可得解.
【解答】(1)证明:因为CC1∥DD1,CF=DG,
所以四边形CFGD为平行四边形,
所以CD=FG,CD∥FG,
又AB=CD,AB∥CD,
所以AB=FG,AB∥FG,
又,,
所以HF=AE,所以四边形HFEA为平行四边形,
所以EF∥AH,
又EF 平面AHD1,AH 平面AHD1,
所以EF∥平面AHD1.
(2)解:以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设正方体棱长为3,则D1(0,0,3),E(3,2,0),F(0,3,1),
所以,
设平面D1EF的法向量为,则,
令y=2,得z=3,,所以,
易知平面ABCD的一个法向量为,
设平面D1EF与平面ABCD夹角的大小为θ,
则,
所以平面D1EF与平面ABCD夹角的余弦值为.
【点评】本题考查立体几何的综合应用,熟练掌握线面平行的判定定理,利用向量法求平面与平面的夹角是解题的关键,考查空间立体感,逻辑推理能力和运算能力,属于中档题.
12.(2024 扬中市校级模拟)如图,在三棱柱ABC﹣A1B1C1中,平面AA1C1C⊥平面ABC,AB=AC=BC=AA1=2,.
(1)证明:AC⊥A1B;
(2)求二面角A﹣CB1﹣B的正弦值.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】(1)证明见解析;(2).
【分析】(1)利用直线与平面垂直证明两直线垂直;(2)利用空间向量法求解二面角的正弦值;
【解答】解:(1)证明:取AC的中点O,则BO⊥AC,且,
因为平面AA1C1C⊥平面ABC,且平面AA1C1C∩平面ABC=AC,BO 平面ABC,
所以BO⊥平面AA1C1C,
因为A1O 平面AA1C1C,
所以BO⊥A1O,
所以,所以,
因为AO=1,AA1=2,所以AO⊥A1O,
又因为AO⊥BO,A1O∩BO=O,A1O,BO 平面A1OB,
所以AC⊥平面A1OB,
又A1B 平面A1OB,
所以AC⊥A1B;
(2)如图所示,以O为原点,OA,OB,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系O﹣xyz,
可得,
因为,
设平面ACB1的法向量为,
则,即得
令y=1,则z=﹣1,
所以,
设平面B1BC的法向量为,
则,即得
令,则n=﹣1,p=1,
所以,
记二面角A﹣CB1﹣B的平面角为α,
因为,
显然sinα>0,所以,
所以二面角A﹣CB1﹣B的正弦值为.
【点评】本题考查线线垂直的判定以及空间向量的应用,属于中档题.
13.(2024 周口二模)如图,在多面体DABCE中,△ABC是等边三角形,AB=AD=2,DB=DC=EB=EC.
(Ⅰ)求证:BC⊥AE;
(Ⅱ)若二面角A﹣BC﹣E为30°,求直线DE与平面ACD所成角的正弦值.
【考点】二面角的平面角及求法;直线与平面所成的角.
【专题】对应思想;综合法;立体几何;逻辑推理;数学运算.
【答案】(Ⅰ)证明见解析;
(Ⅱ).
【分析】(Ⅰ)取BC中点O,连接AO,EO,由题易证AO⊥BC,EO⊥BC,再由垂直的性质定理和判定定理即可得证;
(Ⅱ)先证DO⊥平面ABC,再建系,然后利用空间向量和空间角的关系即可求解.
【解答】(Ⅰ)证明:如图,取BC中点O,连接AO,EO,
∵△ABC是等边三角形,O为BC中点,
∴AO⊥BC,又EB=EC,
∴EO⊥BC,∵AO∩EO=O,
∴BC⊥平面AEO,又AE 平面AEO,
∴BC⊥AE;
解:(Ⅱ)连接DO,则DO⊥BC,由AB=AC=BC=2,,
则,DO=1,又AD=2,
∴AO2+DO2=AD2,
∴DO⊥AO,又AO∩BC=O,
∴DO⊥平面ABC,
如图,以O为坐标原点,OA,OB,OD所在直线分别为x,y,z轴,建立空间直角坐标系,
则O(0,0,0),,C(0,﹣1,0),D(0,0,1),
∴,,
设平面ACD的法向量为,
则,
即,
取x=1,则,
∵∠AOE是二面角A﹣BC﹣E的平面角,
∴∠AOE=30°,又OE=1,
∴,,
设直线DE与平面ACD所成角为θ,
则sinθ=|cos,|,
∴直线DE与平面ACD所成角的正弦值为.
【点评】本题考查了空间几何体中位置关系的证明和空间角的求解,属于中档题.
14.(2024 山西模拟)如图,已知平行六面体ABCD﹣A1B1C1D1的所有棱长均相等,AD⊥平面ABB1A1,P为D1C1的中点,且PD=PC.
(1)求证:CC1⊥BD;
(2)求平面CPB与平面DPB的夹角的正弦值.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;向量法;空间角;数学运算.
【答案】(1)证明过程请见解答;(2).
【分析】(1)设Q是CD的中点,连接PQ,先证CC1⊥CD,由AD⊥平面ABB1A1,知AD⊥AA1,进而得CC1⊥AD,从而有CC1⊥平面ABCD,再由线面垂直的性质定理,即可得证;
(2)先证DA,DC,DD1两两垂直,再以D为坐标原点建立空间直角坐标系,利用向量法求平面与平面的夹角,即可得解.
【解答】(1)证明:设Q是CD的中点,连接PQ,
因为P是C1D1的中点,所以CC1∥PQ,
因为PD=PC,所以PQ⊥CD,所以CC1⊥CD,
因为AD⊥平面ABB1A1,AA1 平面ABB1A1,所以AD⊥AA1,
因为CC1∥AA1,所以CC1⊥AD,
又CD∩AD=D,CD、AD 平面ABCD,
所以CC1⊥平面ABCD,
因为BD 平面ABCD,所以CC1⊥BD.
(2)解:因为AD⊥平面ABB1A1,AB 平面ABB1A1,所以AD⊥AB,
又四边形ABCD的各棱长均相等,
所以四边形ABCD是正方形,
故DA,DC,DD1两两垂直,
以D为坐标原点建立如图所示的空间直角坐标系,
不妨设AD=2,则D(0,0,0),P(0,1,2),B(2,2,0),C(0,2,0),
所以,,,,
设平面DPB的法向量为(x,y,z),则,
令y=﹣2,则(2,﹣2,1),
设平面CPB的法向量为(a,b,c),则,
令c=1,则(0,2,1),
设平面CPB与平面DPB的夹角为θ,则cosθ=|cos,|,
所以,
故平面CPB与平面DPB的夹角的正弦值为.
【点评】本题考查立体几何的综合应用,熟练掌握线面垂直的判定定理与性质定理,利用向量法求平面与平面的夹角是解题的关键,考查空间立体感,逻辑推理能力和运算能力,属于中档题.
15.(2024 保定三模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,AC与BD相交于点E,点F在PC上,.
(1)证明:DF⊥平面PBC;
(2)若PA与平面BDF所成的角为α,平面PAD与平面PBC的夹角为β,求α+β.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】(1)证明见解析;(2)75°.
【分析】(1)通过证明DF⊥PC,DF⊥FB即可证明DF⊥平面PBC;
(2)建立空间直角坐标系,由(1)知PC⊥平面BDF,即可得α=90°﹣∠APC=45°,再求平面PBC和平面PAD的法向量即可求出β.
【解答】解:(1)证明:∵底面ABCD是菱形,∴AC⊥BD,
∵PA⊥平面ABCD,且BD 平面ABCD,
∴PA⊥BD.
又∵AC∩PA=A,AC,PA 平面PAC,
∴BD⊥平面PAC,
∵PC 平面PAC,
∴BD⊥PC,又∵EF⊥PC,且EF,BD 平面BDF,EF∩BD=E,
∴PC⊥平面BDF,∵DF 平面BDF,
∴PC⊥DF,
∵EF=ED=EB=2,
∴∠DFB=90°,即DF⊥FB,又∵PC,FB 平面PBC,且PC∩FB=F,
∴DF⊥平面PBC.
(2)以E为原点,以EA,EB所在直线分别为x轴、y轴,过点E且平行PA的直线为z轴建立空间直角坐标系,如图所示,
则,
∵,
∴,又∵EF⊥PC,
∴在△FEC中由勾股定理得,
即,
∴.∴,
∵,
∴∠ACP=45°,
∴,∴∠APC=45°,
∵PC⊥平面BDF,
∴PA与平面BDF所成的角为α=90°﹣∠APC=45°,
∵DF⊥平面PBC,
∴DF是平面PBC的一个法向量,
∵PA⊥平面ABCD,PA 平面PAD,
∴平面PAD⊥平面ABCD,
设,只需,则平面PAD,
则,
令,则,
∴β=30°,
∴α+β=45°+30°=75°.
【点评】本题考查线面垂直的判定以及空间向量的应用,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 向量在立体几何中的应用
一.选择题(共5小题)
1.(2024 金东区校级模拟)已知矩形ABCD,AB=1,BC,沿对角线AC将△ABC折起,若平面ABC与平面ACD所成角的余弦值为,则B与D之间距离为( )
A.1 B. C. D.
2.(2024 福州期末)如图,ABCD﹣EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到直线AB的距离为( )
A. B. C. D.
3.(2024 肇东市校级期末)已知A(1,0,1),是平面α的一个法向量,且B(﹣1,2,2)是平面α内一点,则点A到平面α的距离为( )
A. B. C. D.
4.(2024 辽阳期末)在平面四边形ABCD中,△ABC为正三角形,AD⊥CD,AD=CD,如图1,将四边形沿AC折起,得到如图2所示的四面体B﹣ACD,若四面体B﹣ACD外接球的球心为O,当四面体B﹣ACD的体积最大时,点O到平面ABD的距离为( )
A. B. C. D.
5.(2024秋 吕梁月考)若平面α的法向量(1,2,﹣3),直线l的方向向量(1,1,1),则( )
A.l∥α B.l⊥α C.l α D.l∥α或l α
二.多选题(共2小题)
(多选)6.(2024 博爱县校级期末)若平面α,β的法向量分别是,,直线l的方向向量为,直线m的方向向量为,则( )
A.α⊥β
B.l∥α
C.l与m为相交直线
D.在上的投影向量为
(多选)7.(2024 南岸区模拟)如图,在正三棱柱ABC﹣A1B1C1中,P为空间一动点,若,则( )
A.若λ=μ,则点P的轨迹为线段BC1
B.若λ+μ=1,则点P的轨迹为线段B1C
C.存在λ,μ∈(0,1),使得AP⊥BC
D.存在λ,μ∈(0,1),使得AP∥平面A1B1C1
三.填空题(共3小题)
8.(2024 徐汇区校级期末)直线m与平面α所成角为60°,则m与平面α内任意直线所成角的取值范围是 .
9.(2024 博白县模拟)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到库底与水坝的交线AB的距离分别为m,CB=5m.又测得AB的长为5m,CD的长为m,则水库底面与水坝斜面所成的二面角的大小为 .
10.(2024 洪山区校级模拟)如图,在直三棱柱ABC﹣A1B1C1中,AA1=3,BC=6,,P为线段A1B1上的一点,且二面角A﹣BC﹣P的正切值为3,则三棱锥A﹣A1C1P的外接球的体积为 .
四.解答题(共5小题)
11.(2024秋 广西月考)如图,在正方体ABCD﹣A1B1C1D1中,点E,F,G分别在AB,CC1,DD1上,且.
(1)若,证明:EF∥平面AHD1.
(2)求平面D1EF与平面ABCD夹角的余弦值.
12.(2024 扬中市校级模拟)如图,在三棱柱ABC﹣A1B1C1中,平面AA1C1C⊥平面ABC,AB=AC=BC=AA1=2,.
(1)证明:AC⊥A1B;
(2)求二面角A﹣CB1﹣B的正弦值.
13.(2024 周口二模)如图,在多面体DABCE中,△ABC是等边三角形,AB=AD=2,DB=DC=EB=EC.
(Ⅰ)求证:BC⊥AE;
(Ⅱ)若二面角A﹣BC﹣E为30°,求直线DE与平面ACD所成角的正弦值.
14.(2024 山西模拟)如图,已知平行六面体ABCD﹣A1B1C1D1的所有棱长均相等,AD⊥平面ABB1A1,P为D1C1的中点,且PD=PC.
(1)求证:CC1⊥BD;
(2)求平面CPB与平面DPB的夹角的正弦值.
15.(2024 保定三模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,AC与BD相交于点E,点F在PC上,.
(1)证明:DF⊥平面PBC;
(2)若PA与平面BDF所成的角为α,平面PAD与平面PBC的夹角为β,求α+β.
新课预习衔接 向量在立体几何中的应用
参考答案与试题解析
一.选择题(共5小题)
1.(2024 金东区校级模拟)已知矩形ABCD,AB=1,BC,沿对角线AC将△ABC折起,若平面ABC与平面ACD所成角的余弦值为,则B与D之间距离为( )
A.1 B. C. D.
【考点】空间向量法求解二面角及两平面的夹角.
【专题】转化思想;向量法;转化法;空间位置关系与距离;数学运算.
【答案】C
【分析】过B和D分别作BE⊥AC,DF⊥AC,根据向量垂直的性质,利用向量数量积进行转化求解即可.
【解答】解:过B和D分别作BE⊥AC,DF⊥AC,
∵AB=1,BC,
∴AC=2,
∵AB BCAC BE,
∴BE=DF,
则AE=CF,即EF=2﹣1=1,
∵平面ABC与平面ACD所成角的余弦值为,
∴cos,,
∵,
∴2=()2222+2 2 2 12|| ||cos,2()3,
则||,
即B与D之间距离为,
故选:C.
【点评】本题主要考查空间两点间距离的计算,利用向量数量积与长度之间的关系进行转化求解是解决本题的关键,是中档题.
2.(2024 福州期末)如图,ABCD﹣EFGH是棱长为1的正方体,若P在正方体内部且满足,则P到直线AB的距离为( )
A. B. C. D.
【考点】空间中点到直线的距离及两平行直线间的距离.
【专题】计算题;转化思想;综合法;空间位置关系与距离;逻辑推理;直观想象;数学运算.
【答案】C
【分析】建立空间直角坐标系,表示出,,进而得到在上的投影向量的长度,即可求出答案.
【解答】解:建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),D(0,1,0),E(0,0,1),
所以(1,0,0),(0,1,0),(0,0,1),
则(1,0,0)(0,1,0)(0,0,1)=(,,),
因为(1,0,0),
所以在上的投影向量的长度为:,
所以点P到AB的距离,
故选:C.
【点评】本题考查点到直线的距离,利用空间直角坐标系是关键,属于中档题.
3.(2024 肇东市校级期末)已知A(1,0,1),是平面α的一个法向量,且B(﹣1,2,2)是平面α内一点,则点A到平面α的距离为( )
A. B. C. D.
【考点】空间中点到平面的距离.
【专题】转化思想;向量法;空间向量及应用;数学运算.
【答案】D
【分析】求出的坐标,再利用点到面的距离公式求解即可.
【解答】解:由已知,又是平面α的一个法向量,
则点A到平面α的距离为.
故选:D.
【点评】本题考查利用向量法求解点到平面的距离,属基础题.
4.(2024 辽阳期末)在平面四边形ABCD中,△ABC为正三角形,AD⊥CD,AD=CD,如图1,将四边形沿AC折起,得到如图2所示的四面体B﹣ACD,若四面体B﹣ACD外接球的球心为O,当四面体B﹣ACD的体积最大时,点O到平面ABD的距离为( )
A. B. C. D.
【考点】空间中点到平面的距离.
【专题】转化思想;综合法;立体几何;数学运算.
【答案】C
【分析】根据题意可得当平面ABC⊥平面ACD时,四面体B﹣ACD的体积最大,在平面ABC内过B作BE⊥AC于点E,则BE⊥平面ACD,再建系,利用向量法,向量数量积运算,即可求解.
【解答】解:根据题意可得当平面ABC⊥平面ACD时,四面体B﹣ACD的体积最大,
在平面ABC内过B作BE⊥AC于点E,则BE⊥平面ACD,
∵△ABC为正三角形,AD⊥CD,易知AC⊥ED,
∴四面体B﹣ACD外接球的球心O为正三角形ABC的中心,即BH的靠近E的三等分点,
建系如图,则根据题意可得:
A(1,0,0),B(0,0,),D(0,1,0),O(0,0,),
∴,,,
设平面ABD的法向量为,
则,取,
∴点O到平面ABD的距离为.
故选:C.
【点评】本题考查向量法求解点面距问题,属中档题.
5.(2024秋 吕梁月考)若平面α的法向量(1,2,﹣3),直线l的方向向量(1,1,1),则( )
A.l∥α B.l⊥α C.l α D.l∥α或l α
【考点】平面的法向量;空间向量的数量积判断向量的共线与垂直;空间直线的方向向量、空间直线的向量参数方程.
【专题】计算题;转化思想;向量法;空间位置关系与距离;数学运算.
【答案】D
【分析】根据法向量与方向向量数量积的运算结果,结合线面关系进行判断即可.
【解答】解:因为,
所以l∥α或l α.
故选:D.
【点评】本题考查了利用向量法判断直线与平面的位置关系,属于基础题.
二.多选题(共2小题)
(多选)6.(2024 博爱县校级期末)若平面α,β的法向量分别是,,直线l的方向向量为,直线m的方向向量为,则( )
A.α⊥β
B.l∥α
C.l与m为相交直线
D.在上的投影向量为
【考点】空间向量语言表述线面的垂直、平行关系;空间向量语言表述面面的垂直、平行关系;空间向量的数量积判断向量的共线与垂直;空间直线的方向向量、空间直线的向量参数方程;平面的法向量.
【专题】计算题;方程思想;转化思想;综合法;空间向量及应用;数学运算.
【答案】AD
【分析】根据题意,由平面与平面垂直的判断方法分析A,由直线与平面的位置关系分析B,由向量平行的方法分析C,由投影向量公式分析D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,平面α,β的法向量分别是,,
由于,则有α⊥β,故A正确;
对于B,,则l∥α或l α,故B错误;
对于C,设,,此方程组无解,则l与为相交直线或异面直线,故C错误;
对于D,在上的投影向量为,故D正确.
故选:AD.
【点评】本题考查空间向量的应用,涉及直线与平面平行、垂直的判断方法,属于基础题.
(多选)7.(2024 南岸区模拟)如图,在正三棱柱ABC﹣A1B1C1中,P为空间一动点,若,则( )
A.若λ=μ,则点P的轨迹为线段BC1
B.若λ+μ=1,则点P的轨迹为线段B1C
C.存在λ,μ∈(0,1),使得AP⊥BC
D.存在λ,μ∈(0,1),使得AP∥平面A1B1C1
【考点】空间向量方法证明线、面的位置关系定理;棱柱的结构特征.
【专题】计算题;方程思想;转化思想;综合法;立体几何;数学抽象.
【答案】ABC
【分析】根据题意,由平面向量基本定理分析A、B、C,由直线与平面平行的性质分析D,综合可得答案.
【解答】解:根据题意,依次分析选项:
对于A,由平面向量基本定理,若,则点P在侧面BCC1B1内(含边界),
又由λ=μ,则,而λ∈[0,1],故点P的轨迹为线段BC1,故A正确;
对于B,若λ+μ=1,则,所以,即,则P在直线B1C上,
又λ∈[0,1],故点P的轨迹为线段B1C,故B正确;
对于C,分别取棱BC,B1C1的中点D,E,连接DE,由于BC⊥AD且BC⊥DE,则BC⊥平面ADEA1,
当点P在线段DE上时,AP⊥BC,故存在λ,μ∈(0,1),使得AP⊥BC,故C正确;
对于D,由直线与平面平行的性质,若AP∥平面A1B1C1,则点P必在棱BC上,此时μ=0,
故不存在λ,μ∈(0,1),使得AP∥平面A1B1C1,故D错误.
故选:ABC.
【点评】本题考查棱柱的结构特征,涉及向量的线性运算,属于中档题.
三.填空题(共3小题)
8.(2024 徐汇区校级期末)直线m与平面α所成角为60°,则m与平面α内任意直线所成角的取值范围是 [,] .
【考点】直线与平面所成的角;异面直线及其所成的角.
【专题】转化思想;综合法;空间角;数学运算.
【答案】[,].
【分析】直线与平面所成的角是直线与平面内任意一条直线所成角中最小的角,结合直线与平面所成角的范围为00≤θ即可得.
【解答】解:直线与平面所成的角是直线与平面内任意一条直线所成角中最小的角,
且直线与平面所成角的范围为0≤θ,
则m与平面α内任意直线所成角的取值范围是[,].
故答案为:[,].
【点评】本题考查直线与平面所成角与异面直线所成角,属于中档题.
9.(2024 博白县模拟)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到库底与水坝的交线AB的距离分别为m,CB=5m.又测得AB的长为5m,CD的长为m,则水库底面与水坝斜面所成的二面角的大小为 .
【考点】二面角的平面角及求法.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】.
【分析】作BE∥AD且BE=AD,连接DE,可得∠CBE是所求二面角的平面角,进而求得BE,CE,再利用余弦定理可求得cos∠CBE,可求得∠CBE.
【解答】解:如图,作BE∥AD且BE=AD,连接DE,又AD⊥AB,则四边形ABED是矩形,
BE⊥AB.又BC⊥AB,所以∠CBE是所求二面角的平面角,
因为DE∥AB,BC⊥AB,则BC⊥DE,
又BE⊥DE,BC∩BE=B,BC,BE 平面BCE,
所以DE⊥平面BCE,而CE 平面BCE,
所以DE⊥CE,DE=AB=5,
所以,,
由题可知BC=5,
则,
又∠CBE是三角形的内角,
所以.
故答案为:.
【点评】本题考查二面角的计算,属于中档题.
10.(2024 洪山区校级模拟)如图,在直三棱柱ABC﹣A1B1C1中,AA1=3,BC=6,,P为线段A1B1上的一点,且二面角A﹣BC﹣P的正切值为3,则三棱锥A﹣A1C1P的外接球的体积为 .
【考点】二面角的平面角及求法;球的体积和表面积.
【专题】计算题;转化思想;综合法;空间位置关系与距离;空间角;直观想象;数学运算.
【答案】.
【分析】根据题意,由条件可得∠PNM是二面角A﹣BC﹣P的平面角,再将三棱锥A﹣A1C1P补为长方体,则长方体的外接球即为三棱锥的外接球,再由球的体积公式,即可得到结果.
【解答】解:如图,作PM∥AA1,交AB于M,则PM=AA1=3,
过M作MN⊥BC交BC于点N,连接PN.
因为ABC﹣A1B1C1为直三棱柱,则AA1⊥平面ABC,且PM∥AA1,
则PM⊥平面ABC,且BC 平面ABC,所以PM⊥BC,
又MN⊥BC,PM∩MN=M,PM,MN 平面PMN,
所以BC⊥平面PMN,PN 平面PMN,所以PN⊥BC,
则∠PNM是二面角A﹣BC﹣P的平面角,
所以,所以MN=1,
又,BC=6,所以,所以,.
可把三棱锥A﹣A1C1P补成棱长为,,3的长方体,
则三棱锥A﹣A1C1P的外接球的半径为,
所以三棱锥A﹣A1C1P的外接球的体积为.
故答案为:.
【点评】本题考查球的体积计算问题,涉及二面角的求法,是中档题.
四.解答题(共5小题)
11.(2024秋 广西月考)如图,在正方体ABCD﹣A1B1C1D1中,点E,F,G分别在AB,CC1,DD1上,且.
(1)若,证明:EF∥平面AHD1.
(2)求平面D1EF与平面ABCD夹角的余弦值.
【考点】空间向量法求解二面角及两平面的夹角;直线与平面平行.
【专题】转化思想;向量法;空间角;数学运算.
【答案】(1)证明过程请见解答;(2).
【分析】(1)先证明四边形HFEA为平行四边形,可得EF∥AH,再由线面平行的判定定理,即可得证;
(2)以D为坐标原点建立空间直角坐标系,利用向量法求平面与平面的夹角,即可得解.
【解答】(1)证明:因为CC1∥DD1,CF=DG,
所以四边形CFGD为平行四边形,
所以CD=FG,CD∥FG,
又AB=CD,AB∥CD,
所以AB=FG,AB∥FG,
又,,
所以HF=AE,所以四边形HFEA为平行四边形,
所以EF∥AH,
又EF 平面AHD1,AH 平面AHD1,
所以EF∥平面AHD1.
(2)解:以D为坐标原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
设正方体棱长为3,则D1(0,0,3),E(3,2,0),F(0,3,1),
所以,
设平面D1EF的法向量为,则,
令y=2,得z=3,,所以,
易知平面ABCD的一个法向量为,
设平面D1EF与平面ABCD夹角的大小为θ,
则,
所以平面D1EF与平面ABCD夹角的余弦值为.
【点评】本题考查立体几何的综合应用,熟练掌握线面平行的判定定理,利用向量法求平面与平面的夹角是解题的关键,考查空间立体感,逻辑推理能力和运算能力,属于中档题.
12.(2024 扬中市校级模拟)如图,在三棱柱ABC﹣A1B1C1中,平面AA1C1C⊥平面ABC,AB=AC=BC=AA1=2,.
(1)证明:AC⊥A1B;
(2)求二面角A﹣CB1﹣B的正弦值.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】(1)证明见解析;(2).
【分析】(1)利用直线与平面垂直证明两直线垂直;(2)利用空间向量法求解二面角的正弦值;
【解答】解:(1)证明:取AC的中点O,则BO⊥AC,且,
因为平面AA1C1C⊥平面ABC,且平面AA1C1C∩平面ABC=AC,BO 平面ABC,
所以BO⊥平面AA1C1C,
因为A1O 平面AA1C1C,
所以BO⊥A1O,
所以,所以,
因为AO=1,AA1=2,所以AO⊥A1O,
又因为AO⊥BO,A1O∩BO=O,A1O,BO 平面A1OB,
所以AC⊥平面A1OB,
又A1B 平面A1OB,
所以AC⊥A1B;
(2)如图所示,以O为原点,OA,OB,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系O﹣xyz,
可得,
因为,
设平面ACB1的法向量为,
则,即得
令y=1,则z=﹣1,
所以,
设平面B1BC的法向量为,
则,即得
令,则n=﹣1,p=1,
所以,
记二面角A﹣CB1﹣B的平面角为α,
因为,
显然sinα>0,所以,
所以二面角A﹣CB1﹣B的正弦值为.
【点评】本题考查线线垂直的判定以及空间向量的应用,属于中档题.
13.(2024 周口二模)如图,在多面体DABCE中,△ABC是等边三角形,AB=AD=2,DB=DC=EB=EC.
(Ⅰ)求证:BC⊥AE;
(Ⅱ)若二面角A﹣BC﹣E为30°,求直线DE与平面ACD所成角的正弦值.
【考点】二面角的平面角及求法;直线与平面所成的角.
【专题】对应思想;综合法;立体几何;逻辑推理;数学运算.
【答案】(Ⅰ)证明见解析;
(Ⅱ).
【分析】(Ⅰ)取BC中点O,连接AO,EO,由题易证AO⊥BC,EO⊥BC,再由垂直的性质定理和判定定理即可得证;
(Ⅱ)先证DO⊥平面ABC,再建系,然后利用空间向量和空间角的关系即可求解.
【解答】(Ⅰ)证明:如图,取BC中点O,连接AO,EO,
∵△ABC是等边三角形,O为BC中点,
∴AO⊥BC,又EB=EC,
∴EO⊥BC,∵AO∩EO=O,
∴BC⊥平面AEO,又AE 平面AEO,
∴BC⊥AE;
解:(Ⅱ)连接DO,则DO⊥BC,由AB=AC=BC=2,,
则,DO=1,又AD=2,
∴AO2+DO2=AD2,
∴DO⊥AO,又AO∩BC=O,
∴DO⊥平面ABC,
如图,以O为坐标原点,OA,OB,OD所在直线分别为x,y,z轴,建立空间直角坐标系,
则O(0,0,0),,C(0,﹣1,0),D(0,0,1),
∴,,
设平面ACD的法向量为,
则,
即,
取x=1,则,
∵∠AOE是二面角A﹣BC﹣E的平面角,
∴∠AOE=30°,又OE=1,
∴,,
设直线DE与平面ACD所成角为θ,
则sinθ=|cos,|,
∴直线DE与平面ACD所成角的正弦值为.
【点评】本题考查了空间几何体中位置关系的证明和空间角的求解,属于中档题.
14.(2024 山西模拟)如图,已知平行六面体ABCD﹣A1B1C1D1的所有棱长均相等,AD⊥平面ABB1A1,P为D1C1的中点,且PD=PC.
(1)求证:CC1⊥BD;
(2)求平面CPB与平面DPB的夹角的正弦值.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;向量法;空间角;数学运算.
【答案】(1)证明过程请见解答;(2).
【分析】(1)设Q是CD的中点,连接PQ,先证CC1⊥CD,由AD⊥平面ABB1A1,知AD⊥AA1,进而得CC1⊥AD,从而有CC1⊥平面ABCD,再由线面垂直的性质定理,即可得证;
(2)先证DA,DC,DD1两两垂直,再以D为坐标原点建立空间直角坐标系,利用向量法求平面与平面的夹角,即可得解.
【解答】(1)证明:设Q是CD的中点,连接PQ,
因为P是C1D1的中点,所以CC1∥PQ,
因为PD=PC,所以PQ⊥CD,所以CC1⊥CD,
因为AD⊥平面ABB1A1,AA1 平面ABB1A1,所以AD⊥AA1,
因为CC1∥AA1,所以CC1⊥AD,
又CD∩AD=D,CD、AD 平面ABCD,
所以CC1⊥平面ABCD,
因为BD 平面ABCD,所以CC1⊥BD.
(2)解:因为AD⊥平面ABB1A1,AB 平面ABB1A1,所以AD⊥AB,
又四边形ABCD的各棱长均相等,
所以四边形ABCD是正方形,
故DA,DC,DD1两两垂直,
以D为坐标原点建立如图所示的空间直角坐标系,
不妨设AD=2,则D(0,0,0),P(0,1,2),B(2,2,0),C(0,2,0),
所以,,,,
设平面DPB的法向量为(x,y,z),则,
令y=﹣2,则(2,﹣2,1),
设平面CPB的法向量为(a,b,c),则,
令c=1,则(0,2,1),
设平面CPB与平面DPB的夹角为θ,则cosθ=|cos,|,
所以,
故平面CPB与平面DPB的夹角的正弦值为.
【点评】本题考查立体几何的综合应用,熟练掌握线面垂直的判定定理与性质定理,利用向量法求平面与平面的夹角是解题的关键,考查空间立体感,逻辑推理能力和运算能力,属于中档题.
15.(2024 保定三模)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,PA⊥平面ABCD,AC与BD相交于点E,点F在PC上,.
(1)证明:DF⊥平面PBC;
(2)若PA与平面BDF所成的角为α,平面PAD与平面PBC的夹角为β,求α+β.
【考点】二面角的平面角及求法;直线与平面垂直.
【专题】转化思想;转化法;立体几何;数学运算.
【答案】(1)证明见解析;(2)75°.
【分析】(1)通过证明DF⊥PC,DF⊥FB即可证明DF⊥平面PBC;
(2)建立空间直角坐标系,由(1)知PC⊥平面BDF,即可得α=90°﹣∠APC=45°,再求平面PBC和平面PAD的法向量即可求出β.
【解答】解:(1)证明:∵底面ABCD是菱形,∴AC⊥BD,
∵PA⊥平面ABCD,且BD 平面ABCD,
∴PA⊥BD.
又∵AC∩PA=A,AC,PA 平面PAC,
∴BD⊥平面PAC,
∵PC 平面PAC,
∴BD⊥PC,又∵EF⊥PC,且EF,BD 平面BDF,EF∩BD=E,
∴PC⊥平面BDF,∵DF 平面BDF,
∴PC⊥DF,
∵EF=ED=EB=2,
∴∠DFB=90°,即DF⊥FB,又∵PC,FB 平面PBC,且PC∩FB=F,
∴DF⊥平面PBC.
(2)以E为原点,以EA,EB所在直线分别为x轴、y轴,过点E且平行PA的直线为z轴建立空间直角坐标系,如图所示,
则,
∵,
∴,又∵EF⊥PC,
∴在△FEC中由勾股定理得,
即,
∴.∴,
∵,
∴∠ACP=45°,
∴,∴∠APC=45°,
∵PC⊥平面BDF,
∴PA与平面BDF所成的角为α=90°﹣∠APC=45°,
∵DF⊥平面PBC,
∴DF是平面PBC的一个法向量,
∵PA⊥平面ABCD,PA 平面PAD,
∴平面PAD⊥平面ABCD,
设,只需,则平面PAD,
则,
令,则,
∴β=30°,
∴α+β=45°+30°=75°.
【点评】本题考查线面垂直的判定以及空间向量的应用,属于中档题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
