初中数学沪科版九年级上册21.4 二次函数的应用 教学设计(表格式)
文档属性
| 名称 | 初中数学沪科版九年级上册21.4 二次函数的应用 教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 202.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 07:11:39 | ||
图片预览

文档简介
课题:21.4二次函数的应用之拱桥问题
教学对象:九年级 课时:1
一、教学内容分析
本节课在二次函数图像和性质的基础上,运用二次函数模型解决生活中的实际问题。学生建立不同的平面直角坐标系,建立不同的二次函数模型,灵活运用二次函数模型解决实际问题,既注重了二次函数的实际应用又培养了学生的综合实践能力,起承上启下的作用,在教材中占据重要地位,在教学中,注重培养学生的建模思想,观察图形、分析问题和解决问题的能力。培养学生应用数学知识解决实际问题的能力。
二、教学目标分析
1:能结合实际图形将问题灵活转化为二次函数问题,利用二次函数的性质解决实际问题; 2:经历将实际问题转化为二次函数问题的过程,体会建模的数学思想及转化、数形结合的思想。 3:体验数学在实际生活中的作用,发展数学思维,提高数学价值,提高应用数学的意识。
三、学情分析
九年级学生已经初步具备解决简单实际问题的知识和能力,但由于函数问题比较抽象,学生从实际问题中抽象出数学模型,利用数学知识来解决实际问题的能力还比较弱。
四、重难点分析
重点:
将实际问题抽象成数学问题,建立二次函数模型,利用二次函数知识解决实际问题。
难点:
将实际问题转化为函数模型
五、教法、学法分析
教法:
问题情境式:从生活中的抛物线形展开,按照从具体实物到物体的运动路径层层推进。注重创设相关知识的问题情境。让学生充分感知数学来源于生活,又服务于生活。 启发式引导式:从提出问题开始,师生共同分析、讨论和探究中拓展学生的思路。
学法:
自主探究,合作交流的学习模式。充分体现了学生的自主地位,充分发挥学生的主动性、合作性和创造性,以达到自主学习、自主发展的目标。
六、教学过程
本节课设五个环节。 环节一:创设情境,引入课题。 环节二:合作探究,归纳建模。 环节三:综合应用,拓展提升。 环节四:归纳总结,达标测评。
具体如下
教师活动 学生活动 设计意图
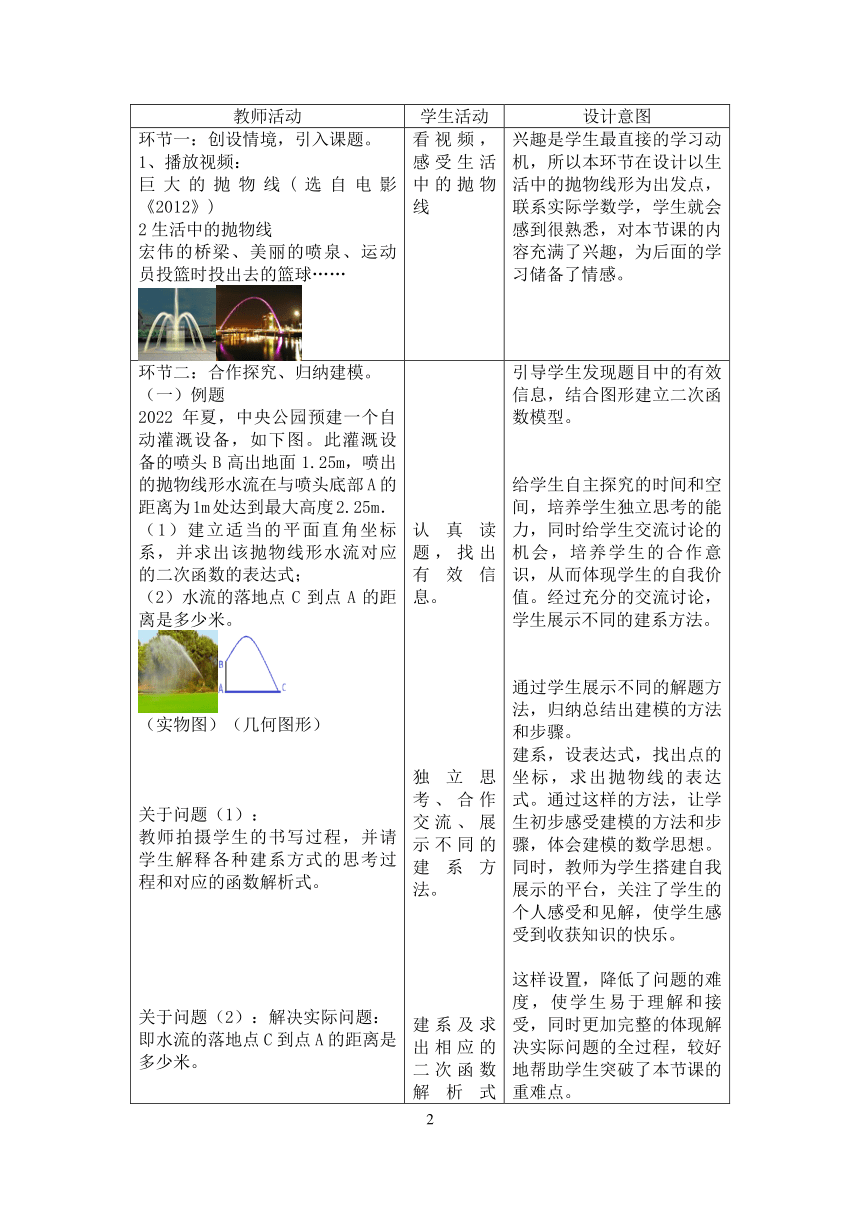
环节一:创设情境,引入课题。 播放视频: 巨大的抛物线(选自电影《2012》) 2生活中的抛物线 宏伟的桥梁、美丽的喷泉、运动员投篮时投出去的篮球…… 看视频,感受生活中的抛物线 兴趣是学生最直接的学习动机,所以本环节在设计以生活中的抛物线形为出发点,联系实际学数学,学生就会感到很熟悉,对本节课的内容充满了兴趣,为后面的学习储备了情感。
环节二:合作探究、归纳建模。 例题 2022年夏,中央公园预建一个自动灌溉设备,如下图。此灌溉设备的喷头B高出地面1.25m,喷出的抛物线形水流在与喷头底部A的距离为1m处达到最大高度2.25m. (1)建立适当的平面直角坐标系,并求出该抛物线形水流对应的二次函数的表达式; (2)水流的落地点C到点A的距离是多少米。 (实物图)(几何图形) 关于问题(1): 教师拍摄学生的书写过程,并请学生解释各种建系方式的思考过程和对应的函数解析式。 关于问题(2):解决实际问题: 即水流的落地点C到点A的距离是多少米。 交流讨论,归纳总结 教师引导学生交流各种不同建系方法,讨论解决抛物线型 实际问题的一般步骤: (1)根据题意建立适当的直角坐标系; (2)把实际问题中的长度转化为点的坐标; (3)合理设出函数解析式; (4)利用待定系数法求出函数解析式; (5)根据求得的解析式进一步分析、判断并进行有关的计算. 环节三:综合应用,拓展提升 巩固练习:1、如图(图形见课件),隧道的截面由抛物线和长方形构成,长方形OABC的长是12m,宽是4m,按照图中所示的平面直角坐标系,抛物线可以用 表示 请写出该抛物线的二次函数解析式。 (2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过? 环节四:归纳总结,达标测评。 归纳总结: 达标测评 如图,“中央公园高塘桥”是抛物线形拱桥,当拱顶离水面2米,水面宽是4米,水面下降1m,水面宽度增加多少?(图见课件) 课堂小结: 谈谈你学习本节课的收获? 布置作业: 课本第38页第2题 认真读题,找出有效信息。 独立思考、合作交流、展示不同的建系方法。 建系及求出相应的二次函数解析式后,将y=0带入求解,并思考解的合理性 整理思路,总结方法,归纳建模的步骤。 读题分析,把题目中的数据在图形中表示出来,求出抛物线的解析式,解决此实际问题 认真思考,积极参与,小组讨论。 用数学的眼光去分析和发现生活中的数学问题。 引导学生发现题目中的有效信息,结合图形建立二次函数模型。 给学生自主探究的时间和空间,培养学生独立思考的能力,同时给学生交流讨论的机会,培养学生的合作意识,从而体现学生的自我价值。经过充分的交流讨论,学生展示不同的建系方法。 通过学生展示不同的解题方法,归纳总结出建模的方法和步骤。 建系,设表达式,找出点的坐标,求出抛物线的表达式。通过这样的方法,让学生初步感受建模的方法和步骤,体会建模的数学思想。同时,教师为学生搭建自我展示的平台,关注了学生的个人感受和见解,使学生感受到收获知识的快乐。 这样设置,降低了问题的难度,使学生易于理解和接受,同时更加完整的体现解决实际问题的全过程,较好地帮助学生突破了本节课的重难点。 让学生明确解题方法,使解题思路更加清晰,再一次强调本节课的重难点。 对前面学习的知识的一个总结和归纳,同时将学会的知识进行一个类比和迁移,进一步体会建模的数学思想。 通过阶梯性问题的设置。有意向的实际问题的难度,目的是巩固和强化利用建模的数学思想来解决实际问题。 为了开阔学生的思路,设置拓展提升,即问题(2),对刚才问题进行拓展,设置汽车能否通过隧道的问题。 这样不仅加深了学生对问题的理解,拓展了学生的思路,同时也把课堂气氛推向了高潮。 帮助学生梳理知识体系,提炼思维方法 通过达标测评,对学生做出真实、可靠并带有鼓励性的评价,目的是帮助学生对自己的所学状况有一个确切的了解,同时也是为了学生巩固所学知识,提高独立思考和灵活运用知识的能力。 教师引导学生谈谈自己在本节课的收获
板书设计 21.4二次函数的应用之拱桥问题 例1
1
教学对象:九年级 课时:1
一、教学内容分析
本节课在二次函数图像和性质的基础上,运用二次函数模型解决生活中的实际问题。学生建立不同的平面直角坐标系,建立不同的二次函数模型,灵活运用二次函数模型解决实际问题,既注重了二次函数的实际应用又培养了学生的综合实践能力,起承上启下的作用,在教材中占据重要地位,在教学中,注重培养学生的建模思想,观察图形、分析问题和解决问题的能力。培养学生应用数学知识解决实际问题的能力。
二、教学目标分析
1:能结合实际图形将问题灵活转化为二次函数问题,利用二次函数的性质解决实际问题; 2:经历将实际问题转化为二次函数问题的过程,体会建模的数学思想及转化、数形结合的思想。 3:体验数学在实际生活中的作用,发展数学思维,提高数学价值,提高应用数学的意识。
三、学情分析
九年级学生已经初步具备解决简单实际问题的知识和能力,但由于函数问题比较抽象,学生从实际问题中抽象出数学模型,利用数学知识来解决实际问题的能力还比较弱。
四、重难点分析
重点:
将实际问题抽象成数学问题,建立二次函数模型,利用二次函数知识解决实际问题。
难点:
将实际问题转化为函数模型
五、教法、学法分析
教法:
问题情境式:从生活中的抛物线形展开,按照从具体实物到物体的运动路径层层推进。注重创设相关知识的问题情境。让学生充分感知数学来源于生活,又服务于生活。 启发式引导式:从提出问题开始,师生共同分析、讨论和探究中拓展学生的思路。
学法:
自主探究,合作交流的学习模式。充分体现了学生的自主地位,充分发挥学生的主动性、合作性和创造性,以达到自主学习、自主发展的目标。
六、教学过程
本节课设五个环节。 环节一:创设情境,引入课题。 环节二:合作探究,归纳建模。 环节三:综合应用,拓展提升。 环节四:归纳总结,达标测评。
具体如下
教师活动 学生活动 设计意图
环节一:创设情境,引入课题。 播放视频: 巨大的抛物线(选自电影《2012》) 2生活中的抛物线 宏伟的桥梁、美丽的喷泉、运动员投篮时投出去的篮球…… 看视频,感受生活中的抛物线 兴趣是学生最直接的学习动机,所以本环节在设计以生活中的抛物线形为出发点,联系实际学数学,学生就会感到很熟悉,对本节课的内容充满了兴趣,为后面的学习储备了情感。
环节二:合作探究、归纳建模。 例题 2022年夏,中央公园预建一个自动灌溉设备,如下图。此灌溉设备的喷头B高出地面1.25m,喷出的抛物线形水流在与喷头底部A的距离为1m处达到最大高度2.25m. (1)建立适当的平面直角坐标系,并求出该抛物线形水流对应的二次函数的表达式; (2)水流的落地点C到点A的距离是多少米。 (实物图)(几何图形) 关于问题(1): 教师拍摄学生的书写过程,并请学生解释各种建系方式的思考过程和对应的函数解析式。 关于问题(2):解决实际问题: 即水流的落地点C到点A的距离是多少米。 交流讨论,归纳总结 教师引导学生交流各种不同建系方法,讨论解决抛物线型 实际问题的一般步骤: (1)根据题意建立适当的直角坐标系; (2)把实际问题中的长度转化为点的坐标; (3)合理设出函数解析式; (4)利用待定系数法求出函数解析式; (5)根据求得的解析式进一步分析、判断并进行有关的计算. 环节三:综合应用,拓展提升 巩固练习:1、如图(图形见课件),隧道的截面由抛物线和长方形构成,长方形OABC的长是12m,宽是4m,按照图中所示的平面直角坐标系,抛物线可以用 表示 请写出该抛物线的二次函数解析式。 (2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过? 环节四:归纳总结,达标测评。 归纳总结: 达标测评 如图,“中央公园高塘桥”是抛物线形拱桥,当拱顶离水面2米,水面宽是4米,水面下降1m,水面宽度增加多少?(图见课件) 课堂小结: 谈谈你学习本节课的收获? 布置作业: 课本第38页第2题 认真读题,找出有效信息。 独立思考、合作交流、展示不同的建系方法。 建系及求出相应的二次函数解析式后,将y=0带入求解,并思考解的合理性 整理思路,总结方法,归纳建模的步骤。 读题分析,把题目中的数据在图形中表示出来,求出抛物线的解析式,解决此实际问题 认真思考,积极参与,小组讨论。 用数学的眼光去分析和发现生活中的数学问题。 引导学生发现题目中的有效信息,结合图形建立二次函数模型。 给学生自主探究的时间和空间,培养学生独立思考的能力,同时给学生交流讨论的机会,培养学生的合作意识,从而体现学生的自我价值。经过充分的交流讨论,学生展示不同的建系方法。 通过学生展示不同的解题方法,归纳总结出建模的方法和步骤。 建系,设表达式,找出点的坐标,求出抛物线的表达式。通过这样的方法,让学生初步感受建模的方法和步骤,体会建模的数学思想。同时,教师为学生搭建自我展示的平台,关注了学生的个人感受和见解,使学生感受到收获知识的快乐。 这样设置,降低了问题的难度,使学生易于理解和接受,同时更加完整的体现解决实际问题的全过程,较好地帮助学生突破了本节课的重难点。 让学生明确解题方法,使解题思路更加清晰,再一次强调本节课的重难点。 对前面学习的知识的一个总结和归纳,同时将学会的知识进行一个类比和迁移,进一步体会建模的数学思想。 通过阶梯性问题的设置。有意向的实际问题的难度,目的是巩固和强化利用建模的数学思想来解决实际问题。 为了开阔学生的思路,设置拓展提升,即问题(2),对刚才问题进行拓展,设置汽车能否通过隧道的问题。 这样不仅加深了学生对问题的理解,拓展了学生的思路,同时也把课堂气氛推向了高潮。 帮助学生梳理知识体系,提炼思维方法 通过达标测评,对学生做出真实、可靠并带有鼓励性的评价,目的是帮助学生对自己的所学状况有一个确切的了解,同时也是为了学生巩固所学知识,提高独立思考和灵活运用知识的能力。 教师引导学生谈谈自己在本节课的收获
板书设计 21.4二次函数的应用之拱桥问题 例1
1
