2024-2025学年期末模拟试卷(含解析)五年级下册数学(北师大版)
文档属性
| 名称 | 2024-2025学年期末模拟试卷(含解析)五年级下册数学(北师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 155.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-12 14:16:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年期末模拟试卷(试题)五年级下册数学(北师大版)
一、单选题
1.水果店运来一些苹果,卖出25.6千克后,还剩下34.9千克,水果店里原来有苹果(用方程解)( )
A.9.3千克 B.60.5千克 C.6.05千克 D.25.6千克
2.下面的展开图中,不能折成正方体的是( )。
A. B.
C. D.
3.如果★代表一个非零自然数,那么下列式子中,结果最大的是( )
A.★× B.★÷ C.÷★ D.★×1
4.如果x、y互为倒数,那么“xy+3”的计算结果是( )
A.3 B.4 C.不能确定
5.用一根铁丝刚好能围 成一个长6cm、宽4cm、高2cm的长方体框架,现在要把这个长方体框架改成一个正方体框架,这个正方体框架的棱长最大是( )cm。
A.4 B.6 C.12 D.24
6.如果把一个鸡蛋完全放入1个装满水的杯子里,溢出的水大约有( )。
A.500mL B.50mL C.51 D.5mL
7.A、B、c都是非0的自然数,如果A× =B× =C× =1,那么( )。
A.A>B>C B.B>A>C C.B>C>A
8.如图,这是一个正方体的展开图。当围成正方体时,与点I重合的点是( )。
A.点A B.点B C.点C
二、判断题
9.所有真分数的倒数一定大于 1 。( )
10.一个数除以 ,这个数就缩小到原来的8倍。( )
11.两个真分数的和仍是真分数。( )
12.长方体、正方体和圆锥的体积公式都可以用V=Sh 表示。( )
13.一个正方体的棱长增加 3cm,它的表面积增加 54 平方厘米。( )
三、填空题
14.要想更清楚地看出两组数据的多少,应绘制 统计图。
15.填上合适的单位。
教室的面积约60
一瓶止咳糖浆的含量是120
一块橡皮的体积约3
1 =1000
16.一个长方体,长8cm,宽6cm,高2cm,它的棱长和是 ,表面积是 ,体积是 。
17.一个正方体的棱长是7厘米,那么它的棱长总和是 厘米,它的表面积是 平方厘米,体积是 立方厘米。
18.一个正方体的表面积是54平方分米,它的体积是 dm3。
19.在括号里填上“>”“<”或“=”。
1.5小时 90分钟 12
20.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的 倍。
21.我国古代数学名著《孙子算经》中记载了一道数学趣题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”若设兔有x只,解决问题正确的方程是 。
四、计算
22.直接写得数。
+
=
+
= 1-
=
-
=
+
=
-
=
+
=
-
=
23.脱式计算,能简算的要简算。
5++ -+ +(-)
24.求下列方程的解。
(1)8x+23=183
(2) x- x=0.15
五、操作题
25.在下图中画一画,表示出×的意义。
六、解决问题
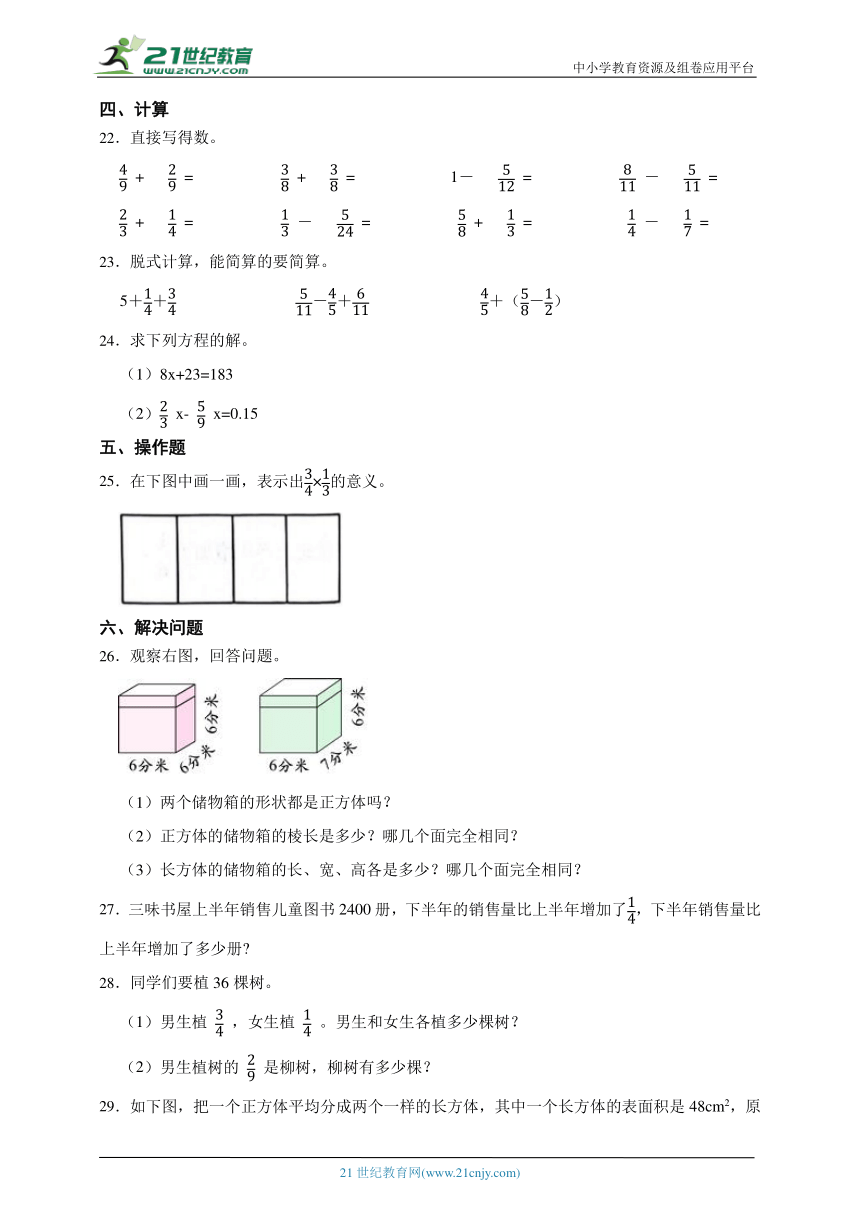
26.观察右图,回答问题。
(1)两个储物箱的形状都是正方体吗?
(2)正方体的储物箱的棱长是多少?哪几个面完全相同?
(3)长方体的储物箱的长、宽、高各是多少?哪几个面完全相同?
27.三味书屋上半年销售儿童图书2400册,下半年的销售量比上半年增加了,下半年销售量比上半年增加了多少册
28.同学们要植36棵树。
(1)男生植 ,女生植 。男生和女生各植多少棵树?
(2)男生植树的 是柳树,柳树有多少棵?
29.如下图,把一个正方体平均分成两个一样的长方体,其中一个长方体的表面积是48cm2,原来的正方体表面积是多少平方厘米?
30.学校组织46名同学和2位老师一起去参观科技馆,买票一共用去1480元。已知每张学生票比成人票便宜20元。每张学生票多少元?每张成人票多少元?
31.一间长8米,宽6米,高2.8米的教室,要粉刷教室的四周,已知门窗共42平方米,如果每平方米涂料用15元,粉刷这间教室一共需多少钱?
答案解析部分
1.【答案】B
【解析】【解答】解:设水果店原来有苹果x千克,
x-25.6=34.9
x-25.6+25.6=34.9+25.6
x=60.5
故答案为:B.
【分析】根据题意可知,设水果店原来有苹果x千克,用原来的苹果质量-卖出的苹果质量=剩下的苹果质量,据此列方程解答.
2.【答案】D
【解析】【解答】解:A项:是正方体展开图的“2-3-1”型;
B项:是正方体展开图的“2-2-2”型;
C项:是正方体展开图的“1-4-1”型;
D项: 不是正方体的展开图,不能折成正方体。
故答案为:D。
【分析】依据正方体展开图的各种类型判断。
3.【答案】B
【解析】【解答】解:解:<1,★×<★;★÷>★;÷★≤;★×1=★;所以结果最大的是★÷。
故答案为:B。
【分析】一个非0数除以一个大于1的数,商小于被除数;一个非0数乘一个小于1的数,积小于这个数;根据计算规律判断得数的大小即可。
4.【答案】B
【解析】【解答】解:x、y互为倒数,则xy=1
所以:
xy+3
=1+3
=4.
故选:B.
【分析】根据倒数的意义,乘积是1的两个数互为倒数.据此解答.
5.【答案】A
【解析】【解答】解: (6 + 4 + 2) × 4 = 48(cm)
48 ÷ 12 = 4(cm)
故答案为:A。
【分析】铁丝长度不变,长方体框架和正方体框架的棱长总和是相等的。因此,我们需要计算长方体框架的棱长总和,然后用这个总和除以12(因为正方体有12条棱),从而得到正方体框架的棱长。
6.【答案】B
【解析】【解答】 如果把一个鸡蛋完全放入1个装满水的杯子里,溢出的水大约有50mL。
故答案为:B。
【分析】这是一道排水法的题目,一个鸡蛋的大小大约是50立方厘米,因为杯子装满水,所以鸡蛋排开的水的体积也是50mL。
7.【答案】C
【解析】【解答】解:因为>>,所以B>C>A。
故答案为:C。
【分析】两个数相乘的积相等,较大的数要乘较小的数。
8.【答案】A
【解析】【解答】解:这是一个正方体的展开图。当围成正方体时,与点I重合的点是A。
故答案为:A。
【分析】如果CDEL为底面,那么ABCD就是后面,KJIH就是前面,由此确定重合的点即可。
9.【答案】正确
【解析】【解答】解:真分数<1,则1÷真分数>1,原题干说法正确。
故答案为:正确。
【分析】真分数<1,求一个数(0除外)的倒数=1÷这个数,则所有真分数的倒数一定大于 1 。
10.【答案】错误
【解析】【解答】解:一个数除以,这个数就扩大到原来的8倍,所以说法错误。
故答案为:错误。
【分析】除以一个数等于乘以这个数的倒数,本题中一个数除以等于这个数乘以8,即这个数扩大到原来的8倍,据此进行判断。
11.【答案】错误
【解析】【解答】解:如:+=,两个真分数的和是假分数;
+=,两个真分数的和是真分数;
+=1,两个真分数的和是整数。
故答案为:错误。
【分析】两个真分数的和可能是假分数、真分数、或者整数。
12.【答案】错误
【解析】【解答】解: 长方体和正方体的体积计算公式都可以用表示,而圆锥的体积计算公式是,不能用表示,所以原说法错误。
故答案为:错误
【分析】长方体和正方体的体积计算公式都可以用表示,其中S是底面积,h是高。圆锥的体积计算公式是,这与长方体和正方体的公式不同。据此解答。
13.【答案】错误
【解析】【解答】解:设正方体原来棱长为a厘米,则原正方体表面积为当棱长增加3厘米,新的棱长变为 (a+3)厘米。新的正方体表面积变为(a+3)×(a+3)×6厘米。
6(a+3)2-6a2
=6(a2+6a+9-a2)
=36a+54。
故答案为:错误。
【分析】由计算结果可以看出,表面积的增加量不仅与增加的棱长相关,还与原棱长直接相关。因此,对于任意的正方体棱长增加3cm,我们不能得出表面积增加54平方厘米的结论,这个增加量还取决于原来的棱长。
14.【答案】复式条形
【解析】【解答】解:要想更清楚地看出两组数据的多少,应绘制复式条形统计图。
故答案为:复式条形。
【分析】条形统计图可以清楚的看出数据的多少;复式条形统计图可以清楚的看出两种数据的多少。
15.【答案】平方米;毫升;立方厘米;千克;克
【解析】【解答】解:教室的面积约60平方米;
一瓶止咳糖浆的含量是120毫升;
一块橡皮的体积约3立方厘米;
1千克=1000克。
故答案为:平方米;毫升;立方厘米;千克;克。
【分析】根据每种事物的实际情况填上合适的单位即可;
进率是1000的单位换算有:1吨=1000千克;1千克=1000克;1升=1000毫升;1立方米=1000立方分米;1立方分米=1000立方厘米,等。
16.【答案】64cm;152cm2;96cm3
【解析】【解答】解:(8+6+2)×4=64cm,(8×6+8×2+6×2)×2=152cm2,8×6×2=96cm3,所以它的棱长和是64cm,表面积是152cm2,体积是96cm3。
故答案为:64cm;152cm2;96cm3。
【分析】长方体的棱长总和=(长+宽+高)×4;长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积=长×宽×高。
17.【答案】84;294;343
【解析】【解答】解:正方体的棱长总和=7×12=84(厘米);
正方体的表面积=7×7×6
=49×6
=294(平方厘米);
正方体的体积=7×7×7
=49×7
=343(立方厘米)。
故答案为:84;294;343。
【分析】正方体的棱长之和=正方体的棱长×12;正方体的表面积=正方体的棱长×正方体的棱长×6;正方体的体积=正方体的棱长×正方体的棱长×正方体的棱长,代入数值计算即可。
18.【答案】729
【解析】【解答】解:54÷6=9(平方分米)
因为3×3=9,所以正方体的棱长是3分米
3×3×3=27(立方分米)
故答案为:27。
【分析】正方体的表面积÷6=正方体一个面的面积;正方体的棱长×棱长=正方体一个面的面积,据此求出正方体的棱长;正方体的棱长×棱长×棱长=正方体的体积。
19.【答案】=;<;=
20.【答案】4
【解析】【解答】解:设小正方体的棱长是a,大正方体的棱长是b。
b×b×6=a×a×6×16
b×b= 4a×4a
所以,b=4a
12×4a÷(12a)
=48a÷12÷a
=4
故答案为:4。
【分析】正方体的表面积=棱长×棱长×6,正方体的棱长之和=棱长×12;根据题意可得:大正方体的棱长×棱长×6=小正方体的棱长×棱长×6×16,据此分别设小正方体的棱长是a,大正方体的棱长是b,代入关系式并化简即可找到大正方体棱长与小正方体棱长的关系,即大正方体的棱长是小正方体棱长的4倍,因此,小正方体的棱长×4×12÷(小正方体的棱长×12)=大正方体的棱长之和是小正方体棱长之和的倍数。
21.【答案】4x+2(35-x)=94
【解析】【解答】解:兔有x只,则雉有(35-x)只。方程:4x+2(35-x)=94。
故答案为:4x+2(35-x)=94。
【分析】此题属于鸡兔同笼问题,雉兔共有35只,脚有94只,先表示出雉的只数,然后根据脚的总数列出方程即可。
22.【答案】+ = + = 1- = - =
+ = - = + = - =
【解析】【分析】同分母分数相加减,分母不变,只把分子相加减;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算。
23.【答案】解:5++
=5+(+)
=5+1
=6
-+
=(+)-
=1-
=
+(-)
=+
=
【解析】【分析】应用加法结合律,先把后面两个数相加,再加上第一个数;
应用加法交换律、加法结合律,变成(+)-,先算括号里面的,再算括号外面的;
先算括号里面的,再算括号外面的。
24.【答案】(1)8x+23=183
解:8x=183-23
8x=160
x=160÷8
x=20
(2) x-x=0.15
解:x=0.15
x=0.15÷
x=1.35
【解析】【分析】综合运用等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等,解方程。
25.【答案】解:橙色部分表示×。
【解析】【分析】×表示把单位“1”平均分成4份,涂色部分占3份,然后把平均分成3份,涂色部分占1份。
26.【答案】(1)解:第一个储物箱的形状是正方体,第二个储物箱的形状是长方体。
(2)解:正方体的储物箱的棱长是6分米;正方体的6个面完全相同。
(3)解:长方体的储物箱的长、宽、高分别是6分米、7分米和6分米;前面和后面完全相同,都是正方形;上、下、左、右4个面完全相同是长方形,长7分米,宽6分米。
【解析】【解答】(1)观察可知,第一个储物箱的形状是正方体,第二个储物箱的形状是长方体;
(2)正方体的储物箱的棱长是6分米,正方体的6个面完全相同;
(3)长方体的储物箱的长、宽、高分别是6分米、7分米和6分米;前面和后面完全相同,都是正方形;上、下、左、右4个面完全相同是长方形,长7分米,宽6分米.
【分析】长方体的特征是:长方体有6个面,每个面都是长方形,也可能相对的两个面是正方形,相对的面完全相同,长方体有12条棱,相对的棱长度相等,长方体有8个顶点;正方体的特征:6个面,6个面是完全相同的正方形,12条棱,棱的长度相等;长方体中相交于一个顶点的三条棱分别叫作长方体的长、宽、高,一般情况下,把底面中较长的一条棱叫作长,较短的一条棱叫作宽,垂直于底面的棱叫作高,据此解答.
27.【答案】解:2400×=600(册)
答:下半年销售量比上半年增加了600册。
【解析】【分析】以上半年的销售量为单位“1”,用上半年销售儿童的册数乘增加的分率即可求出增加的册数。
28.【答案】(1)36×=27(棵)
36×=9(棵)
答:男生植了27棵,女生植了9棵。
(2)27×=6(棵)
答:柳树6棵。
【解析】【分析】(1)植树总棵树×男生植的几分之几=男生植树的棵数;植树总棵树×女生植的几分之几=女生植树的棵数;
(2)男生植树总棵树×柳树占的几分之几=柳树的棵数。
29.【答案】解:48÷4×6
=12×6
=72(平方厘米)
答:原来的正方体表面积是72平方厘米。
【解析】【分析】原来的正方体表面积=原来平均每个面的面积×6;其中,原来平均每个面的面积=一个长方体的表面积÷4。
30.【答案】解:解:设每张学生票为x元,则每张成人票为20+x元,
46x+2×(20+x)=1480
46x+40+2x=1480
48x+40=1480
48x=1480-40
48x=1440
x=1440÷48
x=30
成人票:20+30=50(元)
答:每张学生票30元,每张成人票50元。
【解析】【分析】依据等量关系式:学生票的单价×数量+成人票的单价×数量=总价,求出未知数学生票的单价;成人票的单价=学生票的单价+20元。
31.【答案】解:(8×2.8+6×2.8)×2
=(22.4+16.8)×2
=39.2×2
=78.4(平方米)
78.4-42=36.4(平方米)
36.4×15=546(元)
答:粉刷这间教室一共需546元。
【解析】【分析】粉刷这间教室一共需要的钱数=单价×数量;其中,数量=教室四周的面积-门窗的面积;其中,教室四周的面积=(长×高+宽×高)×2。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年期末模拟试卷(试题)五年级下册数学(北师大版)
一、单选题
1.水果店运来一些苹果,卖出25.6千克后,还剩下34.9千克,水果店里原来有苹果(用方程解)( )
A.9.3千克 B.60.5千克 C.6.05千克 D.25.6千克
2.下面的展开图中,不能折成正方体的是( )。
A. B.
C. D.
3.如果★代表一个非零自然数,那么下列式子中,结果最大的是( )
A.★× B.★÷ C.÷★ D.★×1
4.如果x、y互为倒数,那么“xy+3”的计算结果是( )
A.3 B.4 C.不能确定
5.用一根铁丝刚好能围 成一个长6cm、宽4cm、高2cm的长方体框架,现在要把这个长方体框架改成一个正方体框架,这个正方体框架的棱长最大是( )cm。
A.4 B.6 C.12 D.24
6.如果把一个鸡蛋完全放入1个装满水的杯子里,溢出的水大约有( )。
A.500mL B.50mL C.51 D.5mL
7.A、B、c都是非0的自然数,如果A× =B× =C× =1,那么( )。
A.A>B>C B.B>A>C C.B>C>A
8.如图,这是一个正方体的展开图。当围成正方体时,与点I重合的点是( )。
A.点A B.点B C.点C
二、判断题
9.所有真分数的倒数一定大于 1 。( )
10.一个数除以 ,这个数就缩小到原来的8倍。( )
11.两个真分数的和仍是真分数。( )
12.长方体、正方体和圆锥的体积公式都可以用V=Sh 表示。( )
13.一个正方体的棱长增加 3cm,它的表面积增加 54 平方厘米。( )
三、填空题
14.要想更清楚地看出两组数据的多少,应绘制 统计图。
15.填上合适的单位。
教室的面积约60
一瓶止咳糖浆的含量是120
一块橡皮的体积约3
1 =1000
16.一个长方体,长8cm,宽6cm,高2cm,它的棱长和是 ,表面积是 ,体积是 。
17.一个正方体的棱长是7厘米,那么它的棱长总和是 厘米,它的表面积是 平方厘米,体积是 立方厘米。
18.一个正方体的表面积是54平方分米,它的体积是 dm3。
19.在括号里填上“>”“<”或“=”。
1.5小时 90分钟 12
20.大正方体的表面积是小正方体表面积的16倍,那么大正方体的棱长之和是小正方体的棱长之和的 倍。
21.我国古代数学名著《孙子算经》中记载了一道数学趣题:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”若设兔有x只,解决问题正确的方程是 。
四、计算
22.直接写得数。
+
=
+
= 1-
=
-
=
+
=
-
=
+
=
-
=
23.脱式计算,能简算的要简算。
5++ -+ +(-)
24.求下列方程的解。
(1)8x+23=183
(2) x- x=0.15
五、操作题
25.在下图中画一画,表示出×的意义。
六、解决问题
26.观察右图,回答问题。
(1)两个储物箱的形状都是正方体吗?
(2)正方体的储物箱的棱长是多少?哪几个面完全相同?
(3)长方体的储物箱的长、宽、高各是多少?哪几个面完全相同?
27.三味书屋上半年销售儿童图书2400册,下半年的销售量比上半年增加了,下半年销售量比上半年增加了多少册
28.同学们要植36棵树。
(1)男生植 ,女生植 。男生和女生各植多少棵树?
(2)男生植树的 是柳树,柳树有多少棵?
29.如下图,把一个正方体平均分成两个一样的长方体,其中一个长方体的表面积是48cm2,原来的正方体表面积是多少平方厘米?
30.学校组织46名同学和2位老师一起去参观科技馆,买票一共用去1480元。已知每张学生票比成人票便宜20元。每张学生票多少元?每张成人票多少元?
31.一间长8米,宽6米,高2.8米的教室,要粉刷教室的四周,已知门窗共42平方米,如果每平方米涂料用15元,粉刷这间教室一共需多少钱?
答案解析部分
1.【答案】B
【解析】【解答】解:设水果店原来有苹果x千克,
x-25.6=34.9
x-25.6+25.6=34.9+25.6
x=60.5
故答案为:B.
【分析】根据题意可知,设水果店原来有苹果x千克,用原来的苹果质量-卖出的苹果质量=剩下的苹果质量,据此列方程解答.
2.【答案】D
【解析】【解答】解:A项:是正方体展开图的“2-3-1”型;
B项:是正方体展开图的“2-2-2”型;
C项:是正方体展开图的“1-4-1”型;
D项: 不是正方体的展开图,不能折成正方体。
故答案为:D。
【分析】依据正方体展开图的各种类型判断。
3.【答案】B
【解析】【解答】解:解:<1,★×<★;★÷>★;÷★≤;★×1=★;所以结果最大的是★÷。
故答案为:B。
【分析】一个非0数除以一个大于1的数,商小于被除数;一个非0数乘一个小于1的数,积小于这个数;根据计算规律判断得数的大小即可。
4.【答案】B
【解析】【解答】解:x、y互为倒数,则xy=1
所以:
xy+3
=1+3
=4.
故选:B.
【分析】根据倒数的意义,乘积是1的两个数互为倒数.据此解答.
5.【答案】A
【解析】【解答】解: (6 + 4 + 2) × 4 = 48(cm)
48 ÷ 12 = 4(cm)
故答案为:A。
【分析】铁丝长度不变,长方体框架和正方体框架的棱长总和是相等的。因此,我们需要计算长方体框架的棱长总和,然后用这个总和除以12(因为正方体有12条棱),从而得到正方体框架的棱长。
6.【答案】B
【解析】【解答】 如果把一个鸡蛋完全放入1个装满水的杯子里,溢出的水大约有50mL。
故答案为:B。
【分析】这是一道排水法的题目,一个鸡蛋的大小大约是50立方厘米,因为杯子装满水,所以鸡蛋排开的水的体积也是50mL。
7.【答案】C
【解析】【解答】解:因为>>,所以B>C>A。
故答案为:C。
【分析】两个数相乘的积相等,较大的数要乘较小的数。
8.【答案】A
【解析】【解答】解:这是一个正方体的展开图。当围成正方体时,与点I重合的点是A。
故答案为:A。
【分析】如果CDEL为底面,那么ABCD就是后面,KJIH就是前面,由此确定重合的点即可。
9.【答案】正确
【解析】【解答】解:真分数<1,则1÷真分数>1,原题干说法正确。
故答案为:正确。
【分析】真分数<1,求一个数(0除外)的倒数=1÷这个数,则所有真分数的倒数一定大于 1 。
10.【答案】错误
【解析】【解答】解:一个数除以,这个数就扩大到原来的8倍,所以说法错误。
故答案为:错误。
【分析】除以一个数等于乘以这个数的倒数,本题中一个数除以等于这个数乘以8,即这个数扩大到原来的8倍,据此进行判断。
11.【答案】错误
【解析】【解答】解:如:+=,两个真分数的和是假分数;
+=,两个真分数的和是真分数;
+=1,两个真分数的和是整数。
故答案为:错误。
【分析】两个真分数的和可能是假分数、真分数、或者整数。
12.【答案】错误
【解析】【解答】解: 长方体和正方体的体积计算公式都可以用表示,而圆锥的体积计算公式是,不能用表示,所以原说法错误。
故答案为:错误
【分析】长方体和正方体的体积计算公式都可以用表示,其中S是底面积,h是高。圆锥的体积计算公式是,这与长方体和正方体的公式不同。据此解答。
13.【答案】错误
【解析】【解答】解:设正方体原来棱长为a厘米,则原正方体表面积为当棱长增加3厘米,新的棱长变为 (a+3)厘米。新的正方体表面积变为(a+3)×(a+3)×6厘米。
6(a+3)2-6a2
=6(a2+6a+9-a2)
=36a+54。
故答案为:错误。
【分析】由计算结果可以看出,表面积的增加量不仅与增加的棱长相关,还与原棱长直接相关。因此,对于任意的正方体棱长增加3cm,我们不能得出表面积增加54平方厘米的结论,这个增加量还取决于原来的棱长。
14.【答案】复式条形
【解析】【解答】解:要想更清楚地看出两组数据的多少,应绘制复式条形统计图。
故答案为:复式条形。
【分析】条形统计图可以清楚的看出数据的多少;复式条形统计图可以清楚的看出两种数据的多少。
15.【答案】平方米;毫升;立方厘米;千克;克
【解析】【解答】解:教室的面积约60平方米;
一瓶止咳糖浆的含量是120毫升;
一块橡皮的体积约3立方厘米;
1千克=1000克。
故答案为:平方米;毫升;立方厘米;千克;克。
【分析】根据每种事物的实际情况填上合适的单位即可;
进率是1000的单位换算有:1吨=1000千克;1千克=1000克;1升=1000毫升;1立方米=1000立方分米;1立方分米=1000立方厘米,等。
16.【答案】64cm;152cm2;96cm3
【解析】【解答】解:(8+6+2)×4=64cm,(8×6+8×2+6×2)×2=152cm2,8×6×2=96cm3,所以它的棱长和是64cm,表面积是152cm2,体积是96cm3。
故答案为:64cm;152cm2;96cm3。
【分析】长方体的棱长总和=(长+宽+高)×4;长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积=长×宽×高。
17.【答案】84;294;343
【解析】【解答】解:正方体的棱长总和=7×12=84(厘米);
正方体的表面积=7×7×6
=49×6
=294(平方厘米);
正方体的体积=7×7×7
=49×7
=343(立方厘米)。
故答案为:84;294;343。
【分析】正方体的棱长之和=正方体的棱长×12;正方体的表面积=正方体的棱长×正方体的棱长×6;正方体的体积=正方体的棱长×正方体的棱长×正方体的棱长,代入数值计算即可。
18.【答案】729
【解析】【解答】解:54÷6=9(平方分米)
因为3×3=9,所以正方体的棱长是3分米
3×3×3=27(立方分米)
故答案为:27。
【分析】正方体的表面积÷6=正方体一个面的面积;正方体的棱长×棱长=正方体一个面的面积,据此求出正方体的棱长;正方体的棱长×棱长×棱长=正方体的体积。
19.【答案】=;<;=
20.【答案】4
【解析】【解答】解:设小正方体的棱长是a,大正方体的棱长是b。
b×b×6=a×a×6×16
b×b= 4a×4a
所以,b=4a
12×4a÷(12a)
=48a÷12÷a
=4
故答案为:4。
【分析】正方体的表面积=棱长×棱长×6,正方体的棱长之和=棱长×12;根据题意可得:大正方体的棱长×棱长×6=小正方体的棱长×棱长×6×16,据此分别设小正方体的棱长是a,大正方体的棱长是b,代入关系式并化简即可找到大正方体棱长与小正方体棱长的关系,即大正方体的棱长是小正方体棱长的4倍,因此,小正方体的棱长×4×12÷(小正方体的棱长×12)=大正方体的棱长之和是小正方体棱长之和的倍数。
21.【答案】4x+2(35-x)=94
【解析】【解答】解:兔有x只,则雉有(35-x)只。方程:4x+2(35-x)=94。
故答案为:4x+2(35-x)=94。
【分析】此题属于鸡兔同笼问题,雉兔共有35只,脚有94只,先表示出雉的只数,然后根据脚的总数列出方程即可。
22.【答案】+ = + = 1- = - =
+ = - = + = - =
【解析】【分析】同分母分数相加减,分母不变,只把分子相加减;异分母分数相加减,先通分再按照同分母分数加减法的计算方法计算。
23.【答案】解:5++
=5+(+)
=5+1
=6
-+
=(+)-
=1-
=
+(-)
=+
=
【解析】【分析】应用加法结合律,先把后面两个数相加,再加上第一个数;
应用加法交换律、加法结合律,变成(+)-,先算括号里面的,再算括号外面的;
先算括号里面的,再算括号外面的。
24.【答案】(1)8x+23=183
解:8x=183-23
8x=160
x=160÷8
x=20
(2) x-x=0.15
解:x=0.15
x=0.15÷
x=1.35
【解析】【分析】综合运用等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等,解方程。
25.【答案】解:橙色部分表示×。
【解析】【分析】×表示把单位“1”平均分成4份,涂色部分占3份,然后把平均分成3份,涂色部分占1份。
26.【答案】(1)解:第一个储物箱的形状是正方体,第二个储物箱的形状是长方体。
(2)解:正方体的储物箱的棱长是6分米;正方体的6个面完全相同。
(3)解:长方体的储物箱的长、宽、高分别是6分米、7分米和6分米;前面和后面完全相同,都是正方形;上、下、左、右4个面完全相同是长方形,长7分米,宽6分米。
【解析】【解答】(1)观察可知,第一个储物箱的形状是正方体,第二个储物箱的形状是长方体;
(2)正方体的储物箱的棱长是6分米,正方体的6个面完全相同;
(3)长方体的储物箱的长、宽、高分别是6分米、7分米和6分米;前面和后面完全相同,都是正方形;上、下、左、右4个面完全相同是长方形,长7分米,宽6分米.
【分析】长方体的特征是:长方体有6个面,每个面都是长方形,也可能相对的两个面是正方形,相对的面完全相同,长方体有12条棱,相对的棱长度相等,长方体有8个顶点;正方体的特征:6个面,6个面是完全相同的正方形,12条棱,棱的长度相等;长方体中相交于一个顶点的三条棱分别叫作长方体的长、宽、高,一般情况下,把底面中较长的一条棱叫作长,较短的一条棱叫作宽,垂直于底面的棱叫作高,据此解答.
27.【答案】解:2400×=600(册)
答:下半年销售量比上半年增加了600册。
【解析】【分析】以上半年的销售量为单位“1”,用上半年销售儿童的册数乘增加的分率即可求出增加的册数。
28.【答案】(1)36×=27(棵)
36×=9(棵)
答:男生植了27棵,女生植了9棵。
(2)27×=6(棵)
答:柳树6棵。
【解析】【分析】(1)植树总棵树×男生植的几分之几=男生植树的棵数;植树总棵树×女生植的几分之几=女生植树的棵数;
(2)男生植树总棵树×柳树占的几分之几=柳树的棵数。
29.【答案】解:48÷4×6
=12×6
=72(平方厘米)
答:原来的正方体表面积是72平方厘米。
【解析】【分析】原来的正方体表面积=原来平均每个面的面积×6;其中,原来平均每个面的面积=一个长方体的表面积÷4。
30.【答案】解:解:设每张学生票为x元,则每张成人票为20+x元,
46x+2×(20+x)=1480
46x+40+2x=1480
48x+40=1480
48x=1480-40
48x=1440
x=1440÷48
x=30
成人票:20+30=50(元)
答:每张学生票30元,每张成人票50元。
【解析】【分析】依据等量关系式:学生票的单价×数量+成人票的单价×数量=总价,求出未知数学生票的单价;成人票的单价=学生票的单价+20元。
31.【答案】解:(8×2.8+6×2.8)×2
=(22.4+16.8)×2
=39.2×2
=78.4(平方米)
78.4-42=36.4(平方米)
36.4×15=546(元)
答:粉刷这间教室一共需546元。
【解析】【分析】粉刷这间教室一共需要的钱数=单价×数量;其中,数量=教室四周的面积-门窗的面积;其中,教室四周的面积=(长×高+宽×高)×2。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
