1.1 长度和时间的测量(易错题专项) 课件 人教版(2024)物理八年级上册(30页PPT)
文档属性
| 名称 | 1.1 长度和时间的测量(易错题专项) 课件 人教版(2024)物理八年级上册(30页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-12 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
物理易错题专项—长度和时间的测量
长度、时间、速度核心考点及易错解析
目录
CONTENT
单位换算(十进制 / 千进制)
01
常见估测值
02
刻度尺与停表的使用
03
单位换算(十进制 / 千进制)
R·八年级上册
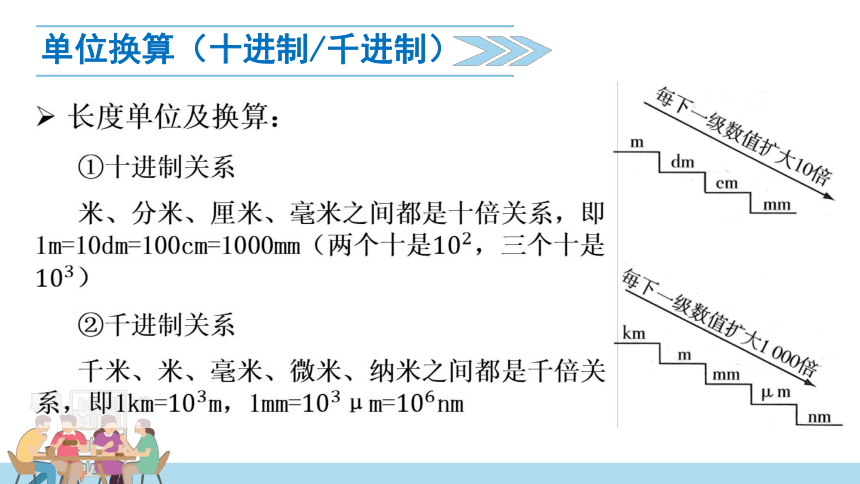
单位换算(十进制/千进制)
长度单位及换算:
①十进制关系
米、分米、厘米、毫米之间都是十倍关系,即1m=10dm=100cm=1000mm(两个十是,三个十是)
②千进制关系
千米、米、毫米、微米、纳米之间都是千倍关系,即1km=m,1mm=μm=nm
换算规则:
大单位→小单位:“乘指数”
如米→毫米:1m × = 1000mm
小单位→大单位:“除指数”
如毫米→米:1000mm ÷ = 1m
进阶换算:
1m= m(×)
1m=nm(×)
单位换算(十进制/千进制)
基础单位换算(大→小)
将下列长度单位换算为指定单位:
① 3.5 千米 = ______ 米
② 2.4 分米 = ______ 厘米
③ 0.08 米 = ______ 毫米
单位换算(十进制/千进制)
3500
24
80
科学计数法换算(小→大)
用科学计数法表示下列单位换算结果:
① 500 微米 = _____ _ 米
② 3 纳米 = 毫米
③ 2400 毫米 = 千米
单位换算(十进制/千进制)
5×\500×
2.4×\2400××
3×\3××
多步骤单位换算
完成下列复杂单位换算:
① 1.2 米 = 微米
② 0.05 毫米 = 纳米
③ 25 厘米 = 千米
单位换算(十进制/千进制)
1.2×\1.2××
2.5×\25××
5×\0.05××
实际应用场景换算
结合生活实例完成换算:
① 一张 A4 纸的厚度约为 0.1 毫米,合 微米。
② 新冠病毒的直径约为 100 纳米,合 米。
③ 珠穆朗玛峰海拔 8848.86 米,合 千米。
单位换算(十进制/千进制)
100\0.1×
1×\100×
8.84886\8848.86×
综合排序与计算
① 将下列长度按从大到小排列:
A. 2 千米 B. 3×10 毫米 C. 4000 厘米 D. 0.5×10 纳米
② 一根钢管长 3.2 米,另一根长 2800 毫米,第三根长 350 厘米,哪根最长?
单位换算(十进制/千进制)
B(3×10 mm=3km)> A(2km)> C(4000cm=40m)> D(0.5×10 nm=0.5m)
统一单位后:
3.2 米 = 320 厘米,2800 毫米 = 280 厘米,350 厘米,第一根最长。
常见估测值
R·八年级上册
常见估测值
生活实例速记:
中学生身高≈1.7m,物理课本长≈26cm,一元硬币直径≈2.5cm,课桌高≈80cm,一层楼高≈3m,门框高≈2m(约为楼层高的 2/3)
估测技巧:
以身体为参照(指甲宽 1cm,一拃20cm)
单位匹配:
长距离用km,微小物体用μm/nm
身体部位参照法:
① 小明用指甲宽度(约 1cm)估测铅笔芯的直径,发现铅笔芯约占指甲宽度的 1/5,铅笔芯直径约为______mm。
② 小红用 “一拃”(约 20cm)测量课桌长度,发现课桌长约 3 拃,课桌长度约为______m。
常见估测值
① 铅笔芯直径 = 1cm×1/5=0.2cm=2mm
② 课桌长度 = 20cm×3=60cm=0.6m
2
0.6
比例关系计算:
① 某楼层高 3m,门框高度约为楼层高度的 2/3,则门框高______m。
② 一张 A4 纸的长度约为物理课本长度(26cm)的 1.5 倍,A4 纸长度约为______cm。
常见估测值
① 门框高度 = 3m×2/3=2m
② A4 纸长度 = 26cm×1.5=39cm
2
39
单位匹配与换算:
① 新冠病毒直径约 100 纳米,合______微米(1 微米 = 1000 纳米)。
② 珠穆朗玛峰海拔 8848.86 米,合 千米。
常见估测值
① 100 纳米 = 100÷1000=0.1 微米
② 8848.86 米 = 8848.86÷1000=8.84886 千米
0.1
8.84886
实际场景估测:
① 中学生身高约 1.7m,教室门高度约为中学生身高的 1.2 倍,教室门高约______m。
② 一元硬币直径 2.5cm,将 10 枚硬币排成一行,总长度约为______cm。
常见估测值
① 门高度 = 1.7m×1.2≈2.04m(接近实际门框高度 2m)
② 总长度 = 2.5cm×10=25cm
2.04
25
综合排序与应用:
① 将下列物体按长度从大到小排列:
A. 物理课本长度(26cm) B. 课桌高度(80cm)
C. 中学生身高(1.7m) D. 一元硬币直径(2.5cm)
② 用 “指甲宽度(1cm)” 估测物理课本厚度,发现课本厚约 5 个指甲宽度,课本厚度约为______mm。
常见估测值
① 排序:C(1.7m)> B(80cm)> A(26cm)> D(2.5cm)
② 课本厚度 = 1cm×5=5cm=50mm
50
刻度尺与停表的使用
R·八年级上册
刻度尺与停表的使用
刻度尺的使用 ——“选、观、放、读、记”
刻度尺的选择与 “三要素” 判断:
① 测量教室的长度,应选择下列哪种刻度尺更合适?( )
A. 量程 0~10cm,分度值 1mm
B. 量程 0~1m,分度值 1cm
C. 量程 0~5m,分度值 1cm
② 某刻度尺标注 “0~20cm”“1mm”,则其量程是_________,分度值是______,若零刻度线磨损,应选__________________作为测量起点。
清晰的整刻度线
C
刻度尺与停表的使用
※教室长度通常 5~10m,需选量程足够且分度值合理的卷尺/ 刻度尺
0~20cm
1mm
刻度尺的放置规范:
测量某物体长度时,如下哪种放置方式正确?( )
方式 A:刻度尺倾斜,刻度线未紧贴物体
方式 B:零刻度线与物体左端对齐,刻度线紧贴物体,与被测边平行
方式 C:零刻度线未对齐物体左端,刻度尺水平放置但刻度线朝上(未紧贴)
B
刻度尺与停表的使用
刻度尺的读数(含估读):
① 某刻度尺分度值为 1mm,测量某物体长度时,末端对齐刻度 “5.32cm”,则物体长度为__________,其中 “5.3cm” 是______值,“0.02cm” 是______值。
② 如图(假设情景:刻度尺分度值 1cm,物体左端对齐 3.0cm 刻度线,右端对齐 9.6cm 刻度线),物体长度为______。
5.32cm
刻度尺与停表的使用
准确
估读
※分度值1mm,需估读到0.1mm即0.01cm
6.6cm
※分度值 1cm,估读到 0.1cm
测量结果的记录规范:
① 某同学测量课本宽度时,读数为 18.5cm,但未写单位,该记录是否正确?为什么?
② 正确测量某物体长度后,记录为 “4.5”,该记录错误在于___________,正确记录应为______(假设分度值 1mm,测量值为 4.50cm)。
刻度尺与停表的使用
缺少单位
① 不正确。测量结果必须包含数值和单位,只写数值无法明确物理意义。
4.50cm
※需体现分度值下一位的估读
综合操作与误差分析:
① 某同学用分度值 1mm 的刻度尺测量铅笔长度,三次测量结果分别为 18.42cm、18.43cm、18.41cm,则铅笔的长度应记为________,多次测量的目的是______________。
② 下列操作会导致测量值偏大的是( )
A. 刻度尺放斜了
B. 刻度线未紧贴被测物体
C. 读数时视线未与刻度线垂直(视线偏低)
D. 零刻度线磨损后,未用末端刻度减起始刻度
刻度尺与停表的使用
减少误差
18.42cm
※B、D 可能导致误差但不一定偏大
A、C
刻度尺与停表的使用
时间单位及停表使用:
单位换算:1h=60min=3600s(60进制),1s=10 ms(千进制)
停表读数规则:
结构:小表盘(分钟)、大表盘(秒)
口诀:“内分外秒,过半读大”
分针未过半→读小刻度(0-30s),分针过半→读大刻度(30-60s)
示例:
小表盘4min,大表盘7.7s(未过半→总时间= 4×60+7.7=247.7s
基础单位换算:
① 3 小时 15 分钟 =____________秒
② 45000 毫秒 =___________分钟
① 3×3600 +15×60 = 11700 秒
② 45000÷1000 =45 秒 → 45÷60 = 0.75 分钟
11700
刻度尺与停表的使用
0.75
停表读数规则应用:
① 小表盘显示 2 分钟,分针未过半,大表盘显示 28.4 秒 → 总时间 =__________秒。
② 小表盘显示 5 分钟,分针过半,大表盘显示 18.3 秒 → 总时间 =__________秒。
① 2×60 +28.4 = 148.4 秒
② 5×60 + (30+18.3)=300+48.3= 348.3 秒
148.4
刻度尺与停表的使用
348.3
复杂单位换算与误差分析:
① 某短跑运动员成绩为 10.5 秒,合______________毫秒,若停表显示小表盘 0 分钟,分针未过半,大表盘 10.5 秒,是否正确?
② 某会议持续时间为 2 小时 45 分钟 30 秒,合__________小时(保留两位小数)
① 10.5×1000 = 10500 毫秒;停表显示错误(10.5 秒超过 0-30 秒范围,分针应过半,大表盘读 10.5 秒需小表盘 0 分钟 + 分针过半)
② 2 +45/60 +30/3600 ≈ 2.76 小时
10500
刻度尺与停表的使用
2.76
停表读数与实际场景结合:
① 实验室测单摆周期,停表显示小表盘 3 分钟,分针过半,大表盘 35.7 秒 → 总时间 =__________秒。
② 某火箭发射倒计时 “10、9、8…1” 共用时 8.5 秒,若停表显示小表盘 0 分钟,分针未过半,大表盘 8.5 秒,是否正确?
② 正确(8.5 秒在 0-30 秒范围内,分针未过半)
① 3×60 +35.7 = 215.7 秒
215.7
刻度尺与停表的使用
综合排序与单位换算:
① 将下列时间按从长到短排序:
A. 1 小时 20 分钟 B. 4500 秒
C. 80000 毫秒 D. 0.5 小时
② 某同学用停表测脉搏,小表盘 0 分钟,分针未过半,大表盘显示 7.2 秒 → 脉搏跳动 10 次用时______秒
② 脉搏时间 =7.2 秒(直接读取大表盘数值)
7.2
刻度尺与停表的使用
① 排序:A(80 分钟)> B(75 分钟)> D(30 分钟)> C(80 秒)
物理易错题专项—长度和时间的测量
长度、时间、速度核心考点及易错解析
目录
CONTENT
单位换算(十进制 / 千进制)
01
常见估测值
02
刻度尺与停表的使用
03
单位换算(十进制 / 千进制)
R·八年级上册
单位换算(十进制/千进制)
长度单位及换算:
①十进制关系
米、分米、厘米、毫米之间都是十倍关系,即1m=10dm=100cm=1000mm(两个十是,三个十是)
②千进制关系
千米、米、毫米、微米、纳米之间都是千倍关系,即1km=m,1mm=μm=nm
换算规则:
大单位→小单位:“乘指数”
如米→毫米:1m × = 1000mm
小单位→大单位:“除指数”
如毫米→米:1000mm ÷ = 1m
进阶换算:
1m= m(×)
1m=nm(×)
单位换算(十进制/千进制)
基础单位换算(大→小)
将下列长度单位换算为指定单位:
① 3.5 千米 = ______ 米
② 2.4 分米 = ______ 厘米
③ 0.08 米 = ______ 毫米
单位换算(十进制/千进制)
3500
24
80
科学计数法换算(小→大)
用科学计数法表示下列单位换算结果:
① 500 微米 = _____ _ 米
② 3 纳米 = 毫米
③ 2400 毫米 = 千米
单位换算(十进制/千进制)
5×\500×
2.4×\2400××
3×\3××
多步骤单位换算
完成下列复杂单位换算:
① 1.2 米 = 微米
② 0.05 毫米 = 纳米
③ 25 厘米 = 千米
单位换算(十进制/千进制)
1.2×\1.2××
2.5×\25××
5×\0.05××
实际应用场景换算
结合生活实例完成换算:
① 一张 A4 纸的厚度约为 0.1 毫米,合 微米。
② 新冠病毒的直径约为 100 纳米,合 米。
③ 珠穆朗玛峰海拔 8848.86 米,合 千米。
单位换算(十进制/千进制)
100\0.1×
1×\100×
8.84886\8848.86×
综合排序与计算
① 将下列长度按从大到小排列:
A. 2 千米 B. 3×10 毫米 C. 4000 厘米 D. 0.5×10 纳米
② 一根钢管长 3.2 米,另一根长 2800 毫米,第三根长 350 厘米,哪根最长?
单位换算(十进制/千进制)
B(3×10 mm=3km)> A(2km)> C(4000cm=40m)> D(0.5×10 nm=0.5m)
统一单位后:
3.2 米 = 320 厘米,2800 毫米 = 280 厘米,350 厘米,第一根最长。
常见估测值
R·八年级上册
常见估测值
生活实例速记:
中学生身高≈1.7m,物理课本长≈26cm,一元硬币直径≈2.5cm,课桌高≈80cm,一层楼高≈3m,门框高≈2m(约为楼层高的 2/3)
估测技巧:
以身体为参照(指甲宽 1cm,一拃20cm)
单位匹配:
长距离用km,微小物体用μm/nm
身体部位参照法:
① 小明用指甲宽度(约 1cm)估测铅笔芯的直径,发现铅笔芯约占指甲宽度的 1/5,铅笔芯直径约为______mm。
② 小红用 “一拃”(约 20cm)测量课桌长度,发现课桌长约 3 拃,课桌长度约为______m。
常见估测值
① 铅笔芯直径 = 1cm×1/5=0.2cm=2mm
② 课桌长度 = 20cm×3=60cm=0.6m
2
0.6
比例关系计算:
① 某楼层高 3m,门框高度约为楼层高度的 2/3,则门框高______m。
② 一张 A4 纸的长度约为物理课本长度(26cm)的 1.5 倍,A4 纸长度约为______cm。
常见估测值
① 门框高度 = 3m×2/3=2m
② A4 纸长度 = 26cm×1.5=39cm
2
39
单位匹配与换算:
① 新冠病毒直径约 100 纳米,合______微米(1 微米 = 1000 纳米)。
② 珠穆朗玛峰海拔 8848.86 米,合 千米。
常见估测值
① 100 纳米 = 100÷1000=0.1 微米
② 8848.86 米 = 8848.86÷1000=8.84886 千米
0.1
8.84886
实际场景估测:
① 中学生身高约 1.7m,教室门高度约为中学生身高的 1.2 倍,教室门高约______m。
② 一元硬币直径 2.5cm,将 10 枚硬币排成一行,总长度约为______cm。
常见估测值
① 门高度 = 1.7m×1.2≈2.04m(接近实际门框高度 2m)
② 总长度 = 2.5cm×10=25cm
2.04
25
综合排序与应用:
① 将下列物体按长度从大到小排列:
A. 物理课本长度(26cm) B. 课桌高度(80cm)
C. 中学生身高(1.7m) D. 一元硬币直径(2.5cm)
② 用 “指甲宽度(1cm)” 估测物理课本厚度,发现课本厚约 5 个指甲宽度,课本厚度约为______mm。
常见估测值
① 排序:C(1.7m)> B(80cm)> A(26cm)> D(2.5cm)
② 课本厚度 = 1cm×5=5cm=50mm
50
刻度尺与停表的使用
R·八年级上册
刻度尺与停表的使用
刻度尺的使用 ——“选、观、放、读、记”
刻度尺的选择与 “三要素” 判断:
① 测量教室的长度,应选择下列哪种刻度尺更合适?( )
A. 量程 0~10cm,分度值 1mm
B. 量程 0~1m,分度值 1cm
C. 量程 0~5m,分度值 1cm
② 某刻度尺标注 “0~20cm”“1mm”,则其量程是_________,分度值是______,若零刻度线磨损,应选__________________作为测量起点。
清晰的整刻度线
C
刻度尺与停表的使用
※教室长度通常 5~10m,需选量程足够且分度值合理的卷尺/ 刻度尺
0~20cm
1mm
刻度尺的放置规范:
测量某物体长度时,如下哪种放置方式正确?( )
方式 A:刻度尺倾斜,刻度线未紧贴物体
方式 B:零刻度线与物体左端对齐,刻度线紧贴物体,与被测边平行
方式 C:零刻度线未对齐物体左端,刻度尺水平放置但刻度线朝上(未紧贴)
B
刻度尺与停表的使用
刻度尺的读数(含估读):
① 某刻度尺分度值为 1mm,测量某物体长度时,末端对齐刻度 “5.32cm”,则物体长度为__________,其中 “5.3cm” 是______值,“0.02cm” 是______值。
② 如图(假设情景:刻度尺分度值 1cm,物体左端对齐 3.0cm 刻度线,右端对齐 9.6cm 刻度线),物体长度为______。
5.32cm
刻度尺与停表的使用
准确
估读
※分度值1mm,需估读到0.1mm即0.01cm
6.6cm
※分度值 1cm,估读到 0.1cm
测量结果的记录规范:
① 某同学测量课本宽度时,读数为 18.5cm,但未写单位,该记录是否正确?为什么?
② 正确测量某物体长度后,记录为 “4.5”,该记录错误在于___________,正确记录应为______(假设分度值 1mm,测量值为 4.50cm)。
刻度尺与停表的使用
缺少单位
① 不正确。测量结果必须包含数值和单位,只写数值无法明确物理意义。
4.50cm
※需体现分度值下一位的估读
综合操作与误差分析:
① 某同学用分度值 1mm 的刻度尺测量铅笔长度,三次测量结果分别为 18.42cm、18.43cm、18.41cm,则铅笔的长度应记为________,多次测量的目的是______________。
② 下列操作会导致测量值偏大的是( )
A. 刻度尺放斜了
B. 刻度线未紧贴被测物体
C. 读数时视线未与刻度线垂直(视线偏低)
D. 零刻度线磨损后,未用末端刻度减起始刻度
刻度尺与停表的使用
减少误差
18.42cm
※B、D 可能导致误差但不一定偏大
A、C
刻度尺与停表的使用
时间单位及停表使用:
单位换算:1h=60min=3600s(60进制),1s=10 ms(千进制)
停表读数规则:
结构:小表盘(分钟)、大表盘(秒)
口诀:“内分外秒,过半读大”
分针未过半→读小刻度(0-30s),分针过半→读大刻度(30-60s)
示例:
小表盘4min,大表盘7.7s(未过半→总时间= 4×60+7.7=247.7s
基础单位换算:
① 3 小时 15 分钟 =____________秒
② 45000 毫秒 =___________分钟
① 3×3600 +15×60 = 11700 秒
② 45000÷1000 =45 秒 → 45÷60 = 0.75 分钟
11700
刻度尺与停表的使用
0.75
停表读数规则应用:
① 小表盘显示 2 分钟,分针未过半,大表盘显示 28.4 秒 → 总时间 =__________秒。
② 小表盘显示 5 分钟,分针过半,大表盘显示 18.3 秒 → 总时间 =__________秒。
① 2×60 +28.4 = 148.4 秒
② 5×60 + (30+18.3)=300+48.3= 348.3 秒
148.4
刻度尺与停表的使用
348.3
复杂单位换算与误差分析:
① 某短跑运动员成绩为 10.5 秒,合______________毫秒,若停表显示小表盘 0 分钟,分针未过半,大表盘 10.5 秒,是否正确?
② 某会议持续时间为 2 小时 45 分钟 30 秒,合__________小时(保留两位小数)
① 10.5×1000 = 10500 毫秒;停表显示错误(10.5 秒超过 0-30 秒范围,分针应过半,大表盘读 10.5 秒需小表盘 0 分钟 + 分针过半)
② 2 +45/60 +30/3600 ≈ 2.76 小时
10500
刻度尺与停表的使用
2.76
停表读数与实际场景结合:
① 实验室测单摆周期,停表显示小表盘 3 分钟,分针过半,大表盘 35.7 秒 → 总时间 =__________秒。
② 某火箭发射倒计时 “10、9、8…1” 共用时 8.5 秒,若停表显示小表盘 0 分钟,分针未过半,大表盘 8.5 秒,是否正确?
② 正确(8.5 秒在 0-30 秒范围内,分针未过半)
① 3×60 +35.7 = 215.7 秒
215.7
刻度尺与停表的使用
综合排序与单位换算:
① 将下列时间按从长到短排序:
A. 1 小时 20 分钟 B. 4500 秒
C. 80000 毫秒 D. 0.5 小时
② 某同学用停表测脉搏,小表盘 0 分钟,分针未过半,大表盘显示 7.2 秒 → 脉搏跳动 10 次用时______秒
② 脉搏时间 =7.2 秒(直接读取大表盘数值)
7.2
刻度尺与停表的使用
① 排序:A(80 分钟)> B(75 分钟)> D(30 分钟)> C(80 秒)
同课章节目录
