2025秋高考物理一轮复习第二章相互作用专题三动态平衡和临界、极值问题课件(49页PPT)
文档属性
| 名称 | 2025秋高考物理一轮复习第二章相互作用专题三动态平衡和临界、极值问题课件(49页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-12 17:57:47 | ||
图片预览









文档简介
(共49张PPT)
第二章 相互作用
专题三 动态平衡和临界、极值问题
素养目标 1.学会用图解法、解析法等解决动态平衡问题.(科学思维) 2.会分析平衡中的临界与极值问题.(科学思维)
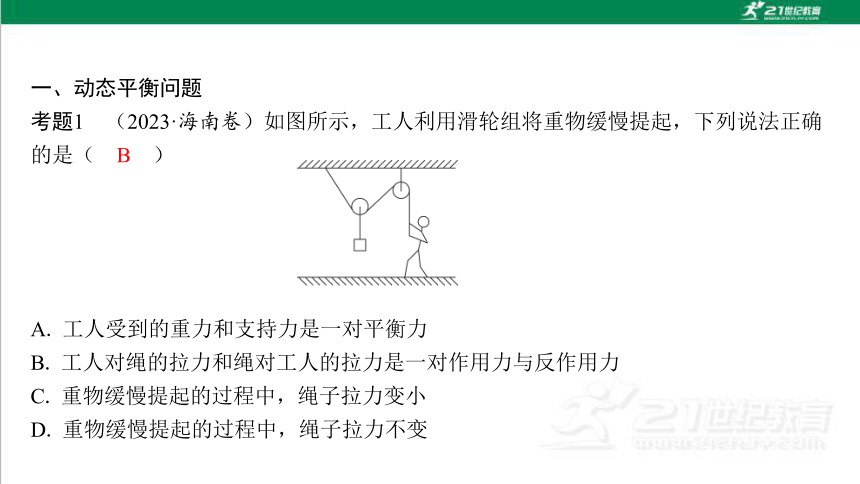
一、动态平衡问题
A. 工人受到的重力和支持力是一对平衡力
B. 工人对绳的拉力和绳对工人的拉力是一对作用力与反作用力
C. 重物缓慢提起的过程中,绳子拉力变小
D. 重物缓慢提起的过程中,绳子拉力不变
B
解析:工人受到三个力的作用,即绳的拉力、地面的支持力和重力,三力平衡,A错误;工人对绳的拉力和绳对工人的拉力是一对作用力与反作用力,B正确;将动滑轮和重物以及两者之间的绳看作一个整体,对整体受力分析,设绕过动滑轮的绳的拉力为T,绳与竖直方向的夹角为θ,动滑轮和重物所受重力为G,由平衡条件有2Tcos θ=G,重物提起过程中,两绳的张角变大,θ变大,拉力T变大,C、D错误.
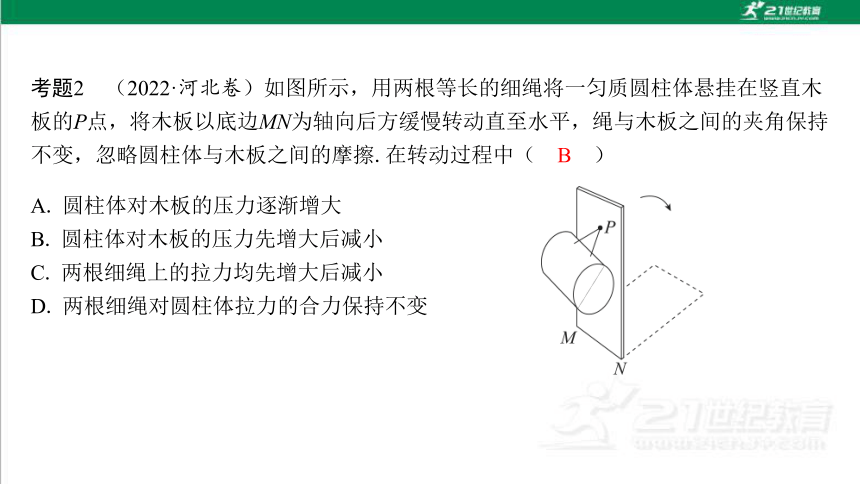
B
A. 圆柱体对木板的压力逐渐增大
B. 圆柱体对木板的压力先增大后减小
C. 两根细绳上的拉力均先增大后减小
D. 两根细绳对圆柱体拉力的合力保持不变
解法二(图像法:作辅助圆)
选圆柱体为研究对象,设两根细绳的拉力的合力为T,除此之外圆柱体还受重力G和木板的支持力N,将三力首尾依次相接构成矢量三角形,如图所示,在木板缓慢转动过程中,两绳拉力的合力T和木板的支持力N同时顺时针转动,重力G恒定,两绳拉力的合力T和木板的支持力N之间的夹角不变,所以矢量三角形外接圆中弦AB所对的角不变,在木板转至水平的过程中,两绳拉力的合力T和木板的弹力N的连接点C由初位置移至B点,由图可知支持力N先增大后减小(由牛顿第三定律可知圆柱体对木板的压力先增大后减小),两绳拉力的合力T一直减小,B正确,A、C、D错误.
深化1 动态平衡:“动态平衡”是指物体的受力状态缓慢发生变化,但变化过程中的每一个状态均可视为平衡状态,所以叫作动态平衡.
解析法 分析研究对象的受力,写出所要分析的力与变化角度的关系式,然后进行数学分析
2Fcos θ=mg
图解法 物体所受的三个力中,如果其中一个力的大小、方向均不变,另一个力的方向不变,求解第三个力的变化时可用图解法
深化2 分析动态平衡问题的方法
相似三
角形法 物体所受的三个力中,如果其中的一个力大小、方向均不变,另外两个力的方向均发生变化,且三个力中没有哪两个力保持垂直关系,可用力三角形与几何三角形相似的方法求解(如△F合BT∽△AOB)
矢量圆法 如图所示,物体受三个共点力作用而平衡,其中一力恒定,另外两力方向一直变化,但两力的夹角不变,作出不同状态的矢量三角形,利用两力夹角不变,可以作出动态圆(也可以由正弦定理列式求解),恒力为圆的一条弦,根据不同位置判断各力的大小变化
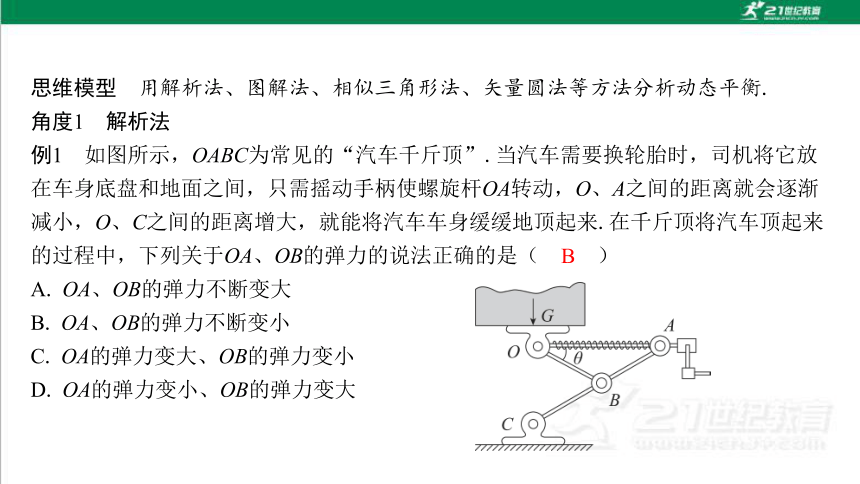
B
A. OA、OB的弹力不断变大
B. OA、OB的弹力不断变小
C. OA的弹力变大、OB的弹力变小
D. OA的弹力变小、OB的弹力变大
角度2 图解法
C
A. T1与T2的合力增大
B. T1与T2的合力减小
C. T1一直增大
D. T2一直减小
解析:由题意知,重物始终处于平衡状态,所以T1与T2的合力与重物重力等大反向,即T1与T2的合力始终保持不变,A、B错误;因为T1与T2的合力F与重物重力等大反向,则对重物受力分析,可得力的矢量三角形如图所示,可以看出,轻绳乙从竖直方向顺时针缓慢旋转至水平过程中,轻绳甲对重物的弹力T1一直增大,当轻绳乙与轻绳甲垂直时,轻绳乙上弹力最小,即轻绳乙对重物的弹力T2先减小后增大,C正确,D错误.
BC
角度3 相似三角形法
A. FT1>FT2 B. FT1=FT2
C. F1<F2 D. F1=F2
角度4 矢量圆法
AD
A. MN上的张力逐渐增大
B. MN上的张力先增大后减小
C. OM上的张力逐渐增大
D. OM上的张力先增大后减小
解析:以重物为研究对象分析受力情况,受重力mg、OM绳上拉力F2、MN上拉力F1,由题意知,三个力的合力始终为零,矢量三角形如图所示,F1、F2的夹角不变,在F2转至水平的过程中,矢量三角形在同一外接圆上,由图可知,MN上的张力F1逐渐增大,OM上的张力F2先增大后减小,所以A、D正确,B、C错误.
二、平衡中的临界、极值问题
B
C. 减小夹角θ,轻绳的合拉力一定减小
D. 轻绳的合拉力最小时,地面对石墩的摩擦力也最小
深化1 临界问题:当某物理量变化时,会引起其他几个物理量的变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,在问题的描述中常用“刚好”“刚能”“恰好”等语言叙述.
临界问题常见的种类:(1)由静止到运动,摩擦力达到最大静摩擦力;(2)绳子恰好绷紧,拉力F=0;(3)刚好离开接触面,支持力F=0.
深化2 极值问题:平衡物体的极值,一般是指在力的变化过程中的最大值和最小值问题.
深化3 解题思路
(1)确定研究对象,并对其受力分析.
(2)画出力的平行四边形或三角形.
(3)明确变量和不变量,结合数学规律对比分析.
(4)动态问题转换为静态问题,抽象问题转换为形象化问题.
深化4 解答平衡中的临界、极值问题的三种方法
图解法 根据平衡条件,作出力的矢量图,通过对物理过程的分析,利用平行四边形定则进行动态分析,确定最大值和最小值
函数法 通过对问题分析,根据平衡条件列出物理量之间的函数关系(画出函数图像),用数学方法求极值(如求二次函数极值、公式极值、三角函数极值)
极限法 正确进行受力分析和变化过程分析,找到平衡的临界点和极值点;临界条件必须在变化中寻找,不能在一个状态上研究临界问题,要把某个物理量推向极大或极小
A. 10 N,30°
C. 25 N,30° D. 25 N,60°
C
角度2 平衡中的临界问题
C
解析:当木板与水平面的夹角为45°时,两物块刚好要滑动,对A物块受力分析如图甲所示,沿斜面方向,A、B之间的滑动摩擦力f1=μN1=μmgcos 45°
根据平衡条件可知T=mgsin 45°+μmgcos 45°
对B物块受力分析如图乙所示,
沿斜面方向,B与斜面之间的滑动摩擦力
f2=μN2=μ·3mgcos 45°
①
根据平衡条件可知
2mgsin 45°=T+μmgcos 45°+μ·3mgcos 45°
①、②两式相加,可得2mgsin 45°=mgsin 45°+2μmgcos 45°+μ·3mgcos 45°
②
限时跟踪检测
A级·基础对点练
题组一 动态平衡问题
A. 摩擦力变小
B. 摩擦力大小不变
C. 弹力变大
D. 弹力变小
D
解析:该过程中蚂蚁受力平衡,设碗弧的切线与水平面的夹角为θ,则Ff=mgsin θ,FN=mgcos θ,由几何知识可知θa<θb,所以Ffa<Ffb,FNa>FNb,故选D.
1
2
3
4
5
6
7
8
9
10
A. 斜面对小球的作用力先减小后增大
B. 挡板对小球的作用力一直增大
C. 挡板对小球的作用力一直减小
D. 挡板与斜面对小球的合力保持不变
D
1
2
3
4
5
6
7
8
9
10
解析:对球受力分析,应用平行四边形定则,如图所示,挡板以底端O点为轴缓慢转到水平位置的过程中,斜面对球的弹力FN2逐渐减小,挡板对球的弹力FN1先减小后增大,故A、B、C错误;小球始终处于平衡状态,所以小球所受的合力始终为零,挡板与斜面对小球的合力与小球的重力等大反向,保持不变,故D正确.
1
2
3
4
5
6
7
8
9
10
A. 外力F大小不变
B. 轻杆对小球的作用力大小变小
C. 地面对木板的支持力逐渐变小
D. 地面对木板的摩擦力逐渐变小
D
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 挡板OA对圆柱的作用力一直增大
B. 挡板OA对圆柱的作用力先增大后减小
C. 挡板OB对圆柱的作用力一直增大
D. 小车对圆柱的作用力先减小后增大
B
1
2
3
4
5
6
7
8
9
10
解析:由题意可知,对圆柱体进行受力分析,如图1所示.将重力、两个弹力平移组成闭合三角形(提示:二力夹角不变,考虑用辅助圆法分析),如图2所示.
两挡板沿逆时针方向缓慢转动至OA水平过程中,两挡板弹力夹角不变,则挡板OA对圆柱的作用力先增大后减小,挡板OB对圆柱的作用力逐渐减小.小车对圆柱的作用力等于mg保持不变,故选B.
1
2
3
4
5
6
7
8
9
10
题组二 平衡中的临界、极值问题
A. 1.5mg B. 1.8mg
C. 2.1mg D. 2.4mg
解析:以a、b、c三球整体为研究对象,所受力的矢量三角形如图所示,当F垂直于T时F最小,Fmin=3mg sin 30°=1.5mg,A正确.
A
1
2
3
4
5
6
7
8
9
10
B. μ>tan α
A
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
B级·能力提升练
A. F1逐渐增大,F2逐渐减小
B. F1逐渐减小,F2逐渐增大
C. F1逐渐减小,F2先增大后减小
D. F1先增大后减小,F2逐渐减小
A
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 地面所受M的压力逐渐增大
B. 地面对M的摩擦力逐渐减小
C. 拉力F的大小从2G逐渐减小为0
D. E、M间的压力从2G逐渐减小到G
BD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10. (1)如图甲所示,三条不可伸长的轻绳结于O点,OC绳将质量为m=1 kg的重物悬挂起来,保持O点的位置不变,改变BO绳拉力方向时,求BO绳拉力的最小值.(重力加速度取10 m/s2,sin 37°=0.6,cos 37°=0.8)
答案:(1)6 N
解析:(1)当BO绳与AO绳垂直时,BO绳的拉力最小,如图所示
根据几何关系有FBO=mgsin 37°=6 N.
1
2
3
4
5
6
7
8
9
10
乙
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
第二章 相互作用
专题三 动态平衡和临界、极值问题
素养目标 1.学会用图解法、解析法等解决动态平衡问题.(科学思维) 2.会分析平衡中的临界与极值问题.(科学思维)
一、动态平衡问题
A. 工人受到的重力和支持力是一对平衡力
B. 工人对绳的拉力和绳对工人的拉力是一对作用力与反作用力
C. 重物缓慢提起的过程中,绳子拉力变小
D. 重物缓慢提起的过程中,绳子拉力不变
B
解析:工人受到三个力的作用,即绳的拉力、地面的支持力和重力,三力平衡,A错误;工人对绳的拉力和绳对工人的拉力是一对作用力与反作用力,B正确;将动滑轮和重物以及两者之间的绳看作一个整体,对整体受力分析,设绕过动滑轮的绳的拉力为T,绳与竖直方向的夹角为θ,动滑轮和重物所受重力为G,由平衡条件有2Tcos θ=G,重物提起过程中,两绳的张角变大,θ变大,拉力T变大,C、D错误.
B
A. 圆柱体对木板的压力逐渐增大
B. 圆柱体对木板的压力先增大后减小
C. 两根细绳上的拉力均先增大后减小
D. 两根细绳对圆柱体拉力的合力保持不变
解法二(图像法:作辅助圆)
选圆柱体为研究对象,设两根细绳的拉力的合力为T,除此之外圆柱体还受重力G和木板的支持力N,将三力首尾依次相接构成矢量三角形,如图所示,在木板缓慢转动过程中,两绳拉力的合力T和木板的支持力N同时顺时针转动,重力G恒定,两绳拉力的合力T和木板的支持力N之间的夹角不变,所以矢量三角形外接圆中弦AB所对的角不变,在木板转至水平的过程中,两绳拉力的合力T和木板的弹力N的连接点C由初位置移至B点,由图可知支持力N先增大后减小(由牛顿第三定律可知圆柱体对木板的压力先增大后减小),两绳拉力的合力T一直减小,B正确,A、C、D错误.
深化1 动态平衡:“动态平衡”是指物体的受力状态缓慢发生变化,但变化过程中的每一个状态均可视为平衡状态,所以叫作动态平衡.
解析法 分析研究对象的受力,写出所要分析的力与变化角度的关系式,然后进行数学分析
2Fcos θ=mg
图解法 物体所受的三个力中,如果其中一个力的大小、方向均不变,另一个力的方向不变,求解第三个力的变化时可用图解法
深化2 分析动态平衡问题的方法
相似三
角形法 物体所受的三个力中,如果其中的一个力大小、方向均不变,另外两个力的方向均发生变化,且三个力中没有哪两个力保持垂直关系,可用力三角形与几何三角形相似的方法求解(如△F合BT∽△AOB)
矢量圆法 如图所示,物体受三个共点力作用而平衡,其中一力恒定,另外两力方向一直变化,但两力的夹角不变,作出不同状态的矢量三角形,利用两力夹角不变,可以作出动态圆(也可以由正弦定理列式求解),恒力为圆的一条弦,根据不同位置判断各力的大小变化
B
A. OA、OB的弹力不断变大
B. OA、OB的弹力不断变小
C. OA的弹力变大、OB的弹力变小
D. OA的弹力变小、OB的弹力变大
角度2 图解法
C
A. T1与T2的合力增大
B. T1与T2的合力减小
C. T1一直增大
D. T2一直减小
解析:由题意知,重物始终处于平衡状态,所以T1与T2的合力与重物重力等大反向,即T1与T2的合力始终保持不变,A、B错误;因为T1与T2的合力F与重物重力等大反向,则对重物受力分析,可得力的矢量三角形如图所示,可以看出,轻绳乙从竖直方向顺时针缓慢旋转至水平过程中,轻绳甲对重物的弹力T1一直增大,当轻绳乙与轻绳甲垂直时,轻绳乙上弹力最小,即轻绳乙对重物的弹力T2先减小后增大,C正确,D错误.
BC
角度3 相似三角形法
A. FT1>FT2 B. FT1=FT2
C. F1<F2 D. F1=F2
角度4 矢量圆法
AD
A. MN上的张力逐渐增大
B. MN上的张力先增大后减小
C. OM上的张力逐渐增大
D. OM上的张力先增大后减小
解析:以重物为研究对象分析受力情况,受重力mg、OM绳上拉力F2、MN上拉力F1,由题意知,三个力的合力始终为零,矢量三角形如图所示,F1、F2的夹角不变,在F2转至水平的过程中,矢量三角形在同一外接圆上,由图可知,MN上的张力F1逐渐增大,OM上的张力F2先增大后减小,所以A、D正确,B、C错误.
二、平衡中的临界、极值问题
B
C. 减小夹角θ,轻绳的合拉力一定减小
D. 轻绳的合拉力最小时,地面对石墩的摩擦力也最小
深化1 临界问题:当某物理量变化时,会引起其他几个物理量的变化,从而使物体所处的平衡状态“恰好出现”或“恰好不出现”,在问题的描述中常用“刚好”“刚能”“恰好”等语言叙述.
临界问题常见的种类:(1)由静止到运动,摩擦力达到最大静摩擦力;(2)绳子恰好绷紧,拉力F=0;(3)刚好离开接触面,支持力F=0.
深化2 极值问题:平衡物体的极值,一般是指在力的变化过程中的最大值和最小值问题.
深化3 解题思路
(1)确定研究对象,并对其受力分析.
(2)画出力的平行四边形或三角形.
(3)明确变量和不变量,结合数学规律对比分析.
(4)动态问题转换为静态问题,抽象问题转换为形象化问题.
深化4 解答平衡中的临界、极值问题的三种方法
图解法 根据平衡条件,作出力的矢量图,通过对物理过程的分析,利用平行四边形定则进行动态分析,确定最大值和最小值
函数法 通过对问题分析,根据平衡条件列出物理量之间的函数关系(画出函数图像),用数学方法求极值(如求二次函数极值、公式极值、三角函数极值)
极限法 正确进行受力分析和变化过程分析,找到平衡的临界点和极值点;临界条件必须在变化中寻找,不能在一个状态上研究临界问题,要把某个物理量推向极大或极小
A. 10 N,30°
C. 25 N,30° D. 25 N,60°
C
角度2 平衡中的临界问题
C
解析:当木板与水平面的夹角为45°时,两物块刚好要滑动,对A物块受力分析如图甲所示,沿斜面方向,A、B之间的滑动摩擦力f1=μN1=μmgcos 45°
根据平衡条件可知T=mgsin 45°+μmgcos 45°
对B物块受力分析如图乙所示,
沿斜面方向,B与斜面之间的滑动摩擦力
f2=μN2=μ·3mgcos 45°
①
根据平衡条件可知
2mgsin 45°=T+μmgcos 45°+μ·3mgcos 45°
①、②两式相加,可得2mgsin 45°=mgsin 45°+2μmgcos 45°+μ·3mgcos 45°
②
限时跟踪检测
A级·基础对点练
题组一 动态平衡问题
A. 摩擦力变小
B. 摩擦力大小不变
C. 弹力变大
D. 弹力变小
D
解析:该过程中蚂蚁受力平衡,设碗弧的切线与水平面的夹角为θ,则Ff=mgsin θ,FN=mgcos θ,由几何知识可知θa<θb,所以Ffa<Ffb,FNa>FNb,故选D.
1
2
3
4
5
6
7
8
9
10
A. 斜面对小球的作用力先减小后增大
B. 挡板对小球的作用力一直增大
C. 挡板对小球的作用力一直减小
D. 挡板与斜面对小球的合力保持不变
D
1
2
3
4
5
6
7
8
9
10
解析:对球受力分析,应用平行四边形定则,如图所示,挡板以底端O点为轴缓慢转到水平位置的过程中,斜面对球的弹力FN2逐渐减小,挡板对球的弹力FN1先减小后增大,故A、B、C错误;小球始终处于平衡状态,所以小球所受的合力始终为零,挡板与斜面对小球的合力与小球的重力等大反向,保持不变,故D正确.
1
2
3
4
5
6
7
8
9
10
A. 外力F大小不变
B. 轻杆对小球的作用力大小变小
C. 地面对木板的支持力逐渐变小
D. 地面对木板的摩擦力逐渐变小
D
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 挡板OA对圆柱的作用力一直增大
B. 挡板OA对圆柱的作用力先增大后减小
C. 挡板OB对圆柱的作用力一直增大
D. 小车对圆柱的作用力先减小后增大
B
1
2
3
4
5
6
7
8
9
10
解析:由题意可知,对圆柱体进行受力分析,如图1所示.将重力、两个弹力平移组成闭合三角形(提示:二力夹角不变,考虑用辅助圆法分析),如图2所示.
两挡板沿逆时针方向缓慢转动至OA水平过程中,两挡板弹力夹角不变,则挡板OA对圆柱的作用力先增大后减小,挡板OB对圆柱的作用力逐渐减小.小车对圆柱的作用力等于mg保持不变,故选B.
1
2
3
4
5
6
7
8
9
10
题组二 平衡中的临界、极值问题
A. 1.5mg B. 1.8mg
C. 2.1mg D. 2.4mg
解析:以a、b、c三球整体为研究对象,所受力的矢量三角形如图所示,当F垂直于T时F最小,Fmin=3mg sin 30°=1.5mg,A正确.
A
1
2
3
4
5
6
7
8
9
10
B. μ>tan α
A
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
B级·能力提升练
A. F1逐渐增大,F2逐渐减小
B. F1逐渐减小,F2逐渐增大
C. F1逐渐减小,F2先增大后减小
D. F1先增大后减小,F2逐渐减小
A
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
A. 地面所受M的压力逐渐增大
B. 地面对M的摩擦力逐渐减小
C. 拉力F的大小从2G逐渐减小为0
D. E、M间的压力从2G逐渐减小到G
BD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10. (1)如图甲所示,三条不可伸长的轻绳结于O点,OC绳将质量为m=1 kg的重物悬挂起来,保持O点的位置不变,改变BO绳拉力方向时,求BO绳拉力的最小值.(重力加速度取10 m/s2,sin 37°=0.6,cos 37°=0.8)
答案:(1)6 N
解析:(1)当BO绳与AO绳垂直时,BO绳的拉力最小,如图所示
根据几何关系有FBO=mgsin 37°=6 N.
1
2
3
4
5
6
7
8
9
10
乙
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
同课章节目录
