21.3 二次函数与一元二次方程 同步练习(含答案)
文档属性
| 名称 | 21.3 二次函数与一元二次方程 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
21.3 二次函数与一元二次方程
一、单选题
1.(2024九上·安宁月考)关于二次函数的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线
C.顶点坐标是 D.与轴有两个交点
2.(2016九上·达拉特旗期末)已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为( )
A.k>- B.k>- 且k≠0
C.k≥- D.k≥- 且k≠0
3.(2024九上·海安期中)对于二次函数的图象,下列说法正确的是( )
A.与y轴交点坐标为 B.与x轴有两个公共点
C.当时,y随x增大而减小 D.对称轴为直线
4.(2024九上·兰州期中)根据下列表格对应值:判断关于的方程的一个解的范围是( )
3.24 3.25 3.26
0.01 0.03
A. B.
C. D.
5.(2024九下·池州模拟)二次函数图象如图.下列结论:①;②;③若m为任意实数,则有;④若,且,则;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(2024九上·苍南期中)二次函数的顶点坐标为,则实数c的值为( )
A. B. C.4 D.16
7.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0)一个解x的取值范围是( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
﹣0.05
﹣0.01
0.04
0.08
A.1.23<x<1.24 B.1.24<x<1.25
C.1.25<x<1.26 D.1<x<1.23
8.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
9.(2023九上·宁波期末)如图所示为二次函数的图象,对称轴是直线,下列结论:;;;;其中正确的个数是( )
A.1 B.2 C.3 D.4
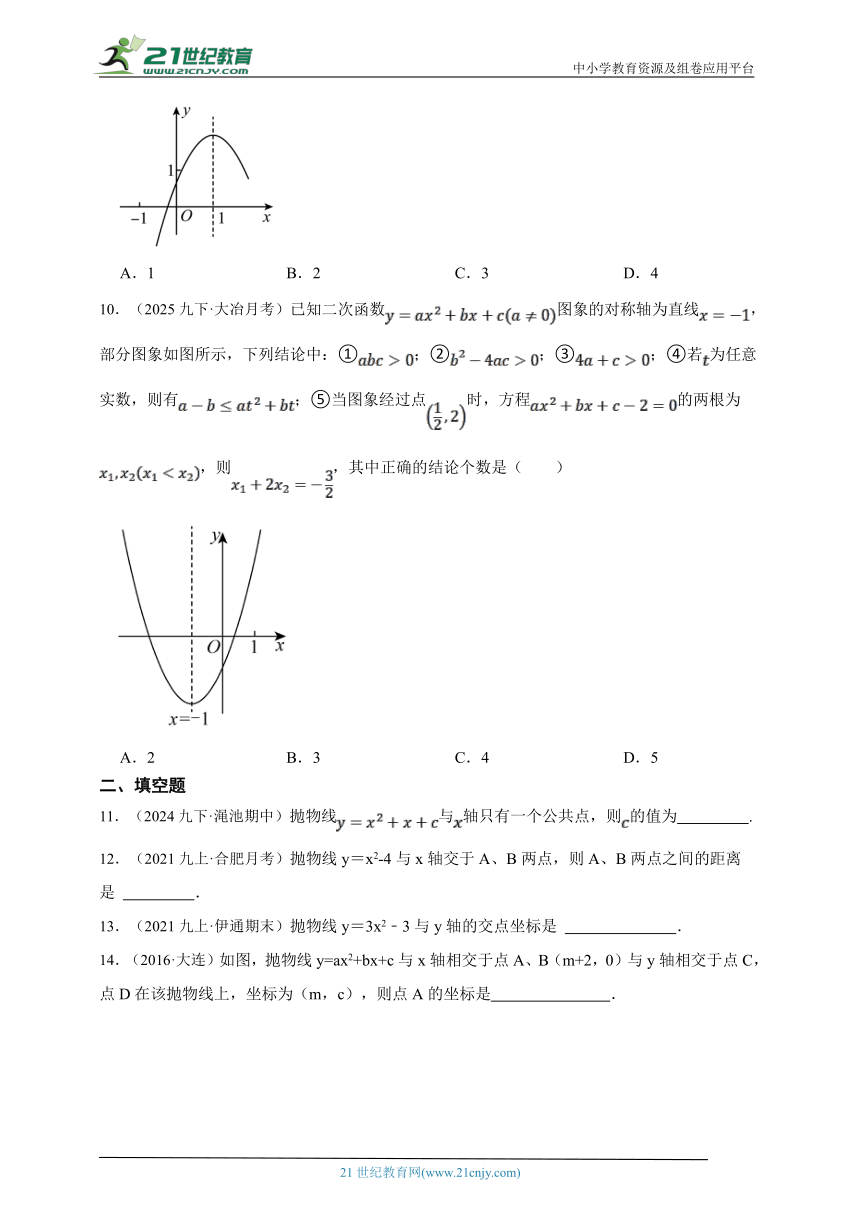
10.(2025九下·大冶月考)已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若为任意实数,则有;⑤当图象经过点时,方程的两根为,则,其中正确的结论个数是( )
A.2 B.3 C.4 D.5
二、填空题
11.(2024九下·渑池期中)抛物线与轴只有一个公共点,则的值为 .
12.(2021九上·合肥月考)抛物线y=x2-4与x轴交于A、B两点,则A、B两点之间的距离是 .
13.(2021九上·伊通期末)抛物线y=3x2﹣3与y轴的交点坐标是 .
14.(2016·大连)如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
15.(2017九上·宁城期末)设抛物线y= +8x-k的顶点在x轴上,则k= .
16.(2025九下·昌平开学考)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
三、计算题
17.(2024九上·潼南月考)(1)求一元二次方程的根;
(2)求抛物线与轴的交点坐标.
18.(2019九下·新乐开学考)已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
19.(2019·广东模拟)如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
20.(2023九下·桐乡市开学考)已知二次函数,的图象如图所示.
(1)求y的取值范围;
(2)若直线与该函数图象只有一个交点,直接写出k的取值范围.
21.(2024九上·姑苏月考)已知抛物线,根据下列条件,求值:
(1)抛物线的顶点在轴上;
(2)抛物线的顶点在轴上.
22.(2023九上·盐山月考)已知关于x的一元二次方程:.
(1)当时,解方程;
(2)若的一个解是,求k的值;
(3)若抛物线与x轴无交点,请确定k的取值范围.
23.(2024九上·北京市月考)在平面直角坐标系中,已知抛物线G:.
(1)直接写出抛物线G的顶点坐标;
(2)若在抛物线G上有两点,,且,直接写出n的取值范围;
(3)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段恰有一个公共点,结合图象,求m的取值范围.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】C
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
7.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
11.【答案】
【知识点】二次函数图象与坐标轴的交点问题
12.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
13.【答案】(0,-3)
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】(﹣2,0)
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】-16
【知识点】二次函数图象与坐标轴的交点问题
16.【答案】②④
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
17.【答案】(1),;(2),
【知识点】公式法解一元二次方程;二次函数图象与坐标轴的交点问题
18.【答案】解:令 , 则
解关于 的方程得 ,
设 ,
∵
∴ 或
∴ 或
解得 , ,经检验 , 是分式方程的根.
∴m的值为2或 .
【知识点】二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
19.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
20.【答案】(1)
(2)或
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题
21.【答案】(1)2
(2)0
【知识点】二次函数图象与坐标轴的交点问题
22.【答案】(1)解:将代入
则方程为,,,
,,
故方程的解为,
(2)解:将代入得:
,∴得
(3)解:由可知,∴
∵令△<0,则原方程无解,∴,∴,即时,抛物线与x轴无交点.
【知识点】配方法解一元二次方程;二次函数图象与坐标轴的交点问题
23.【答案】(1)
(2)或
(3)或
【知识点】二次函数图象与坐标轴的交点问题
21.3 二次函数与一元二次方程
一、单选题
1.(2024九上·安宁月考)关于二次函数的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线
C.顶点坐标是 D.与轴有两个交点
2.(2016九上·达拉特旗期末)已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为( )
A.k>- B.k>- 且k≠0
C.k≥- D.k≥- 且k≠0
3.(2024九上·海安期中)对于二次函数的图象,下列说法正确的是( )
A.与y轴交点坐标为 B.与x轴有两个公共点
C.当时,y随x增大而减小 D.对称轴为直线
4.(2024九上·兰州期中)根据下列表格对应值:判断关于的方程的一个解的范围是( )
3.24 3.25 3.26
0.01 0.03
A. B.
C. D.
5.(2024九下·池州模拟)二次函数图象如图.下列结论:①;②;③若m为任意实数,则有;④若,且,则;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(2024九上·苍南期中)二次函数的顶点坐标为,则实数c的值为( )
A. B. C.4 D.16
7.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0)一个解x的取值范围是( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
﹣0.05
﹣0.01
0.04
0.08
A.1.23<x<1.24 B.1.24<x<1.25
C.1.25<x<1.26 D.1<x<1.23
8.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
9.(2023九上·宁波期末)如图所示为二次函数的图象,对称轴是直线,下列结论:;;;;其中正确的个数是( )
A.1 B.2 C.3 D.4
10.(2025九下·大冶月考)已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若为任意实数,则有;⑤当图象经过点时,方程的两根为,则,其中正确的结论个数是( )
A.2 B.3 C.4 D.5
二、填空题
11.(2024九下·渑池期中)抛物线与轴只有一个公共点,则的值为 .
12.(2021九上·合肥月考)抛物线y=x2-4与x轴交于A、B两点,则A、B两点之间的距离是 .
13.(2021九上·伊通期末)抛物线y=3x2﹣3与y轴的交点坐标是 .
14.(2016·大连)如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
15.(2017九上·宁城期末)设抛物线y= +8x-k的顶点在x轴上,则k= .
16.(2025九下·昌平开学考)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
三、计算题
17.(2024九上·潼南月考)(1)求一元二次方程的根;
(2)求抛物线与轴的交点坐标.
18.(2019九下·新乐开学考)已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
19.(2019·广东模拟)如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
20.(2023九下·桐乡市开学考)已知二次函数,的图象如图所示.
(1)求y的取值范围;
(2)若直线与该函数图象只有一个交点,直接写出k的取值范围.
21.(2024九上·姑苏月考)已知抛物线,根据下列条件,求值:
(1)抛物线的顶点在轴上;
(2)抛物线的顶点在轴上.
22.(2023九上·盐山月考)已知关于x的一元二次方程:.
(1)当时,解方程;
(2)若的一个解是,求k的值;
(3)若抛物线与x轴无交点,请确定k的取值范围.
23.(2024九上·北京市月考)在平面直角坐标系中,已知抛物线G:.
(1)直接写出抛物线G的顶点坐标;
(2)若在抛物线G上有两点,,且,直接写出n的取值范围;
(3)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段恰有一个公共点,结合图象,求m的取值范围.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】C
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
7.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
11.【答案】
【知识点】二次函数图象与坐标轴的交点问题
12.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
13.【答案】(0,-3)
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】(﹣2,0)
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】-16
【知识点】二次函数图象与坐标轴的交点问题
16.【答案】②④
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
17.【答案】(1),;(2),
【知识点】公式法解一元二次方程;二次函数图象与坐标轴的交点问题
18.【答案】解:令 , 则
解关于 的方程得 ,
设 ,
∵
∴ 或
∴ 或
解得 , ,经检验 , 是分式方程的根.
∴m的值为2或 .
【知识点】二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
19.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
20.【答案】(1)
(2)或
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题
21.【答案】(1)2
(2)0
【知识点】二次函数图象与坐标轴的交点问题
22.【答案】(1)解:将代入
则方程为,,,
,,
故方程的解为,
(2)解:将代入得:
,∴得
(3)解:由可知,∴
∵令△<0,则原方程无解,∴,∴,即时,抛物线与x轴无交点.
【知识点】配方法解一元二次方程;二次函数图象与坐标轴的交点问题
23.【答案】(1)
(2)或
(3)或
【知识点】二次函数图象与坐标轴的交点问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
21.3 二次函数与一元二次方程
一、单选题
1.(2024九上·安宁月考)关于二次函数的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线
C.顶点坐标是 D.与轴有两个交点
2.(2016九上·达拉特旗期末)已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为( )
A.k>- B.k>- 且k≠0
C.k≥- D.k≥- 且k≠0
3.(2024九上·海安期中)对于二次函数的图象,下列说法正确的是( )
A.与y轴交点坐标为 B.与x轴有两个公共点
C.当时,y随x增大而减小 D.对称轴为直线
4.(2024九上·兰州期中)根据下列表格对应值:判断关于的方程的一个解的范围是( )
3.24 3.25 3.26
0.01 0.03
A. B.
C. D.
5.(2024九下·池州模拟)二次函数图象如图.下列结论:①;②;③若m为任意实数,则有;④若,且,则;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(2024九上·苍南期中)二次函数的顶点坐标为,则实数c的值为( )
A. B. C.4 D.16
7.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0)一个解x的取值范围是( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
﹣0.05
﹣0.01
0.04
0.08
A.1.23<x<1.24 B.1.24<x<1.25
C.1.25<x<1.26 D.1<x<1.23
8.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
9.(2023九上·宁波期末)如图所示为二次函数的图象,对称轴是直线,下列结论:;;;;其中正确的个数是( )
A.1 B.2 C.3 D.4
10.(2025九下·大冶月考)已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若为任意实数,则有;⑤当图象经过点时,方程的两根为,则,其中正确的结论个数是( )
A.2 B.3 C.4 D.5
二、填空题
11.(2024九下·渑池期中)抛物线与轴只有一个公共点,则的值为 .
12.(2021九上·合肥月考)抛物线y=x2-4与x轴交于A、B两点,则A、B两点之间的距离是 .
13.(2021九上·伊通期末)抛物线y=3x2﹣3与y轴的交点坐标是 .
14.(2016·大连)如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
15.(2017九上·宁城期末)设抛物线y= +8x-k的顶点在x轴上,则k= .
16.(2025九下·昌平开学考)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
三、计算题
17.(2024九上·潼南月考)(1)求一元二次方程的根;
(2)求抛物线与轴的交点坐标.
18.(2019九下·新乐开学考)已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
19.(2019·广东模拟)如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
20.(2023九下·桐乡市开学考)已知二次函数,的图象如图所示.
(1)求y的取值范围;
(2)若直线与该函数图象只有一个交点,直接写出k的取值范围.
21.(2024九上·姑苏月考)已知抛物线,根据下列条件,求值:
(1)抛物线的顶点在轴上;
(2)抛物线的顶点在轴上.
22.(2023九上·盐山月考)已知关于x的一元二次方程:.
(1)当时,解方程;
(2)若的一个解是,求k的值;
(3)若抛物线与x轴无交点,请确定k的取值范围.
23.(2024九上·北京市月考)在平面直角坐标系中,已知抛物线G:.
(1)直接写出抛物线G的顶点坐标;
(2)若在抛物线G上有两点,,且,直接写出n的取值范围;
(3)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段恰有一个公共点,结合图象,求m的取值范围.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】C
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
7.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
11.【答案】
【知识点】二次函数图象与坐标轴的交点问题
12.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
13.【答案】(0,-3)
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】(﹣2,0)
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】-16
【知识点】二次函数图象与坐标轴的交点问题
16.【答案】②④
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
17.【答案】(1),;(2),
【知识点】公式法解一元二次方程;二次函数图象与坐标轴的交点问题
18.【答案】解:令 , 则
解关于 的方程得 ,
设 ,
∵
∴ 或
∴ 或
解得 , ,经检验 , 是分式方程的根.
∴m的值为2或 .
【知识点】二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
19.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
20.【答案】(1)
(2)或
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题
21.【答案】(1)2
(2)0
【知识点】二次函数图象与坐标轴的交点问题
22.【答案】(1)解:将代入
则方程为,,,
,,
故方程的解为,
(2)解:将代入得:
,∴得
(3)解:由可知,∴
∵令△<0,则原方程无解,∴,∴,即时,抛物线与x轴无交点.
【知识点】配方法解一元二次方程;二次函数图象与坐标轴的交点问题
23.【答案】(1)
(2)或
(3)或
【知识点】二次函数图象与坐标轴的交点问题
21.3 二次函数与一元二次方程
一、单选题
1.(2024九上·安宁月考)关于二次函数的图象,下列说法正确的是( )
A.开口向下 B.对称轴是直线
C.顶点坐标是 D.与轴有两个交点
2.(2016九上·达拉特旗期末)已知二次函数y=kx2-7x-7的图象与x轴有两个交点,则k的取值范围为( )
A.k>- B.k>- 且k≠0
C.k≥- D.k≥- 且k≠0
3.(2024九上·海安期中)对于二次函数的图象,下列说法正确的是( )
A.与y轴交点坐标为 B.与x轴有两个公共点
C.当时,y随x增大而减小 D.对称轴为直线
4.(2024九上·兰州期中)根据下列表格对应值:判断关于的方程的一个解的范围是( )
3.24 3.25 3.26
0.01 0.03
A. B.
C. D.
5.(2024九下·池州模拟)二次函数图象如图.下列结论:①;②;③若m为任意实数,则有;④若,且,则;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.(2024九上·苍南期中)二次函数的顶点坐标为,则实数c的值为( )
A. B. C.4 D.16
7.根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0)一个解x的取值范围是( )
x
1.23
1.24
1.25
1.26
ax2+bx+c
﹣0.05
﹣0.01
0.04
0.08
A.1.23<x<1.24 B.1.24<x<1.25
C.1.25<x<1.26 D.1<x<1.23
8.(2025·邛崃模拟)某同学用描点法画二次函数的图象时,列出了下面的表格,请你根据获得的信息分析下列四个结论,其中正确的是( )
A.对称轴为
B.关于的一元二次方程只有一个根
C.当时,随的减小而减小
D.二次函数图象的顶点坐标为
9.(2023九上·宁波期末)如图所示为二次函数的图象,对称轴是直线,下列结论:;;;;其中正确的个数是( )
A.1 B.2 C.3 D.4
10.(2025九下·大冶月考)已知二次函数图象的对称轴为直线,部分图象如图所示,下列结论中:①;②;③;④若为任意实数,则有;⑤当图象经过点时,方程的两根为,则,其中正确的结论个数是( )
A.2 B.3 C.4 D.5
二、填空题
11.(2024九下·渑池期中)抛物线与轴只有一个公共点,则的值为 .
12.(2021九上·合肥月考)抛物线y=x2-4与x轴交于A、B两点,则A、B两点之间的距离是 .
13.(2021九上·伊通期末)抛物线y=3x2﹣3与y轴的交点坐标是 .
14.(2016·大连)如图,抛物线y=ax2+bx+c与x轴相交于点A、B(m+2,0)与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是 .
15.(2017九上·宁城期末)设抛物线y= +8x-k的顶点在x轴上,则k= .
16.(2025九下·昌平开学考)如图,在平面直角坐标系中,已知点,其中,抛物线经过点和,以下四个结论:
①;②;③关于的一元二次方程无实根;④点,在抛物线上且在对称轴的同侧,当时,总有时,则.其中所有正确结论的序号是 .
三、计算题
17.(2024九上·潼南月考)(1)求一元二次方程的根;
(2)求抛物线与轴的交点坐标.
18.(2019九下·新乐开学考)已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴相交于A、B两点,且AB=2,求m的值.
19.(2019·广东模拟)如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
四、解答题
20.(2023九下·桐乡市开学考)已知二次函数,的图象如图所示.
(1)求y的取值范围;
(2)若直线与该函数图象只有一个交点,直接写出k的取值范围.
21.(2024九上·姑苏月考)已知抛物线,根据下列条件,求值:
(1)抛物线的顶点在轴上;
(2)抛物线的顶点在轴上.
22.(2023九上·盐山月考)已知关于x的一元二次方程:.
(1)当时,解方程;
(2)若的一个解是,求k的值;
(3)若抛物线与x轴无交点,请确定k的取值范围.
23.(2024九上·北京市月考)在平面直角坐标系中,已知抛物线G:.
(1)直接写出抛物线G的顶点坐标;
(2)若在抛物线G上有两点,,且,直接写出n的取值范围;
(3)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段恰有一个公共点,结合图象,求m的取值范围.
答案解析部分
1.【答案】C
【知识点】二次函数图象与坐标轴的交点问题
2.【答案】B
【知识点】二次函数图象与坐标轴的交点问题
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
5.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
6.【答案】C
【知识点】一元二次方程根的判别式及应用;二次函数图象与坐标轴的交点问题
7.【答案】B
【知识点】利用二次函数图象求一元二次方程的近似根
8.【答案】D
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
9.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
10.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
11.【答案】
【知识点】二次函数图象与坐标轴的交点问题
12.【答案】4
【知识点】二次函数图象与坐标轴的交点问题
13.【答案】(0,-3)
【知识点】二次函数图象与坐标轴的交点问题
14.【答案】(﹣2,0)
【知识点】二次函数图象与坐标轴的交点问题
15.【答案】-16
【知识点】二次函数图象与坐标轴的交点问题
16.【答案】②④
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
17.【答案】(1),;(2),
【知识点】公式法解一元二次方程;二次函数图象与坐标轴的交点问题
18.【答案】解:令 , 则
解关于 的方程得 ,
设 ,
∵
∴ 或
∴ 或
解得 , ,经检验 , 是分式方程的根.
∴m的值为2或 .
【知识点】二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征
19.【答案】(1)将点A(-1,0),B(4,0)的坐标代入函数的表达式得:
,
解得:b=3,c=4.
抛物线的解析式为y=-x2+3x+4.
(2)如图1所示: ∵令x=0得y=4, ∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°, ∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,-a2+3a+4)(a>0).
则CF=a,PF=|-a2+3a+4-4|=|a2-3a|.
∴|a2-3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)如图2所示:连接EC. 设点P的坐标为(a,-a2+3a+4).则OE=a,PE=-a2+3a+4,EB=4-a.
∵S四边形PCEB= OB PE= ×4(-a2+3a+4),S△CEB= EB OC= ×4×(4-a),
∴S△PBC=S四边形PCEB-S△CEB=2(-a2+3a+4)-2(4-a)=-2a2+8a.
∵a=-2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;二次函数-动态几何问题
20.【答案】(1)
(2)或
【知识点】二次函数的最值;二次函数图象与坐标轴的交点问题
21.【答案】(1)2
(2)0
【知识点】二次函数图象与坐标轴的交点问题
22.【答案】(1)解:将代入
则方程为,,,
,,
故方程的解为,
(2)解:将代入得:
,∴得
(3)解:由可知,∴
∵令△<0,则原方程无解,∴,∴,即时,抛物线与x轴无交点.
【知识点】配方法解一元二次方程;二次函数图象与坐标轴的交点问题
23.【答案】(1)
(2)或
(3)或
【知识点】二次函数图象与坐标轴的交点问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
