21.4 二次函数的应用 同步练习(含答案)
文档属性
| 名称 | 21.4 二次函数的应用 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 11:41:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
21.4 二次函数的应用
一、单选题
1.(2024九下·江阴模拟)某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
2.(2024九上·汉阳期中)如图,一名男生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,他推出铅球的距离为( )
A. B. C. D.
3.(2022九上·顺平期中)某书店销售某种中考复习资料,若每本可获利元,一天可售出本,则该书店出售该种中考复习资料的日利润最大为( )
A.250元 B.500元 C.750元 D.1000元
4.(2023九上·武汉月考)某超市一月份的营业额为万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,则根据题意列方程为( )
A. B.
C. D.
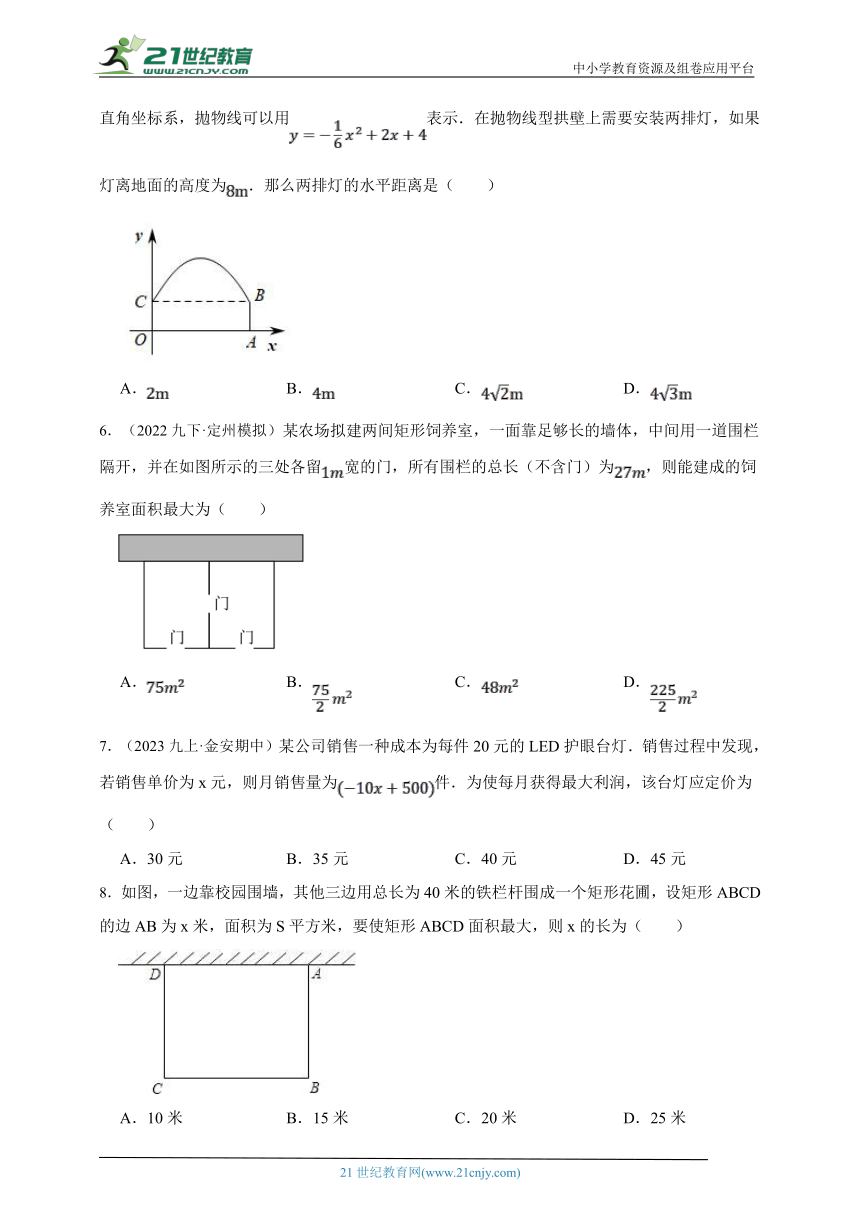
5.(2024九下·嘉禾期中)如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
6.(2022九下·定州模拟)某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的三处各留宽的门,所有围栏的总长(不含门)为,则能建成的饲养室面积最大为( )
A. B. C. D.
7.(2023九上·金安期中)某公司销售一种成本为每件20元的LED护眼台灯.销售过程中发现,若销售单价为x元,则月销售量为件.为使每月获得最大利润,该台灯应定价为( )
A.30元 B.35元 C.40元 D.45元
8.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
9.(2018九上·绍兴期中)已知如图,抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,垂足为Q,当∠ACH=∠CPQ时,此时CP的长为()
A. B. C. D.
10.(2020九上·霸州期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( )
A.①④ B.②④ C.①③ D.②③
二、填空题
11.(2023九上·招远期中)如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是,则选取点B为坐标原点时的抛物线表达式是 .
12.(2023九上·平邑月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出千克,经调查,售价每降元,每天多卖千克,另外,每天的其它固定成本元.当定价为 元能获得最大利润.
13.(2024九上·济宁月考)一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的函数关系式是,则他将铅球推出的距离是 m.
14.(2021九上·雄县)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为 ;
(2)日销售的最大利润为 元.
15.(2023·平凉模拟) 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则小球飞行最大高度是
16.(2023九上·上虞月考)如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
(1)如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .
(2)如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .
三、计算题
17.(2025·罗湖模拟)抖音直播购物逐渐走进了人们的生活.为提高我县特产红富士苹果的影响力,某电商在抖音平台上对我县红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可售出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.若想通过涨价增加每日利润,设涨价后的售价为元,每日获得的利润为元.
(1)涨价后每日销量将减少______件(用含的代数式表示);
(2)当售价为多少时,每日获的利润最大?最大利润为多少?
18.(2023九上·新会期中)一名男生推铅球,铅球的行进高度(单位:)与水平距离(单位:)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4.
19.(2024九上·大安期中)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
四、解答题
20.(2024九上·黑龙江期中)如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
(1)几秒后四边形APQC的面积是19平方厘米;
(2)若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.
21.(2023九上·杭州月考)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度与水平距离之间的关系式是.
(1)水流喷出的最大高度是多少?
(2)若不计其他因素,水池的半径至少为多少,才能使喷出的水流不落在池外?
22.(2025九上·门头沟期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
23.(2024九下·凉州期中)如图,已知抛物线经过,,三点,其顶点为,对称轴是直线,与轴交于点.
(1)求该抛物线的解析式;
(2)若点是该抛物线对称轴上的一个动点,求周长的最小值;
(3)如图(2),若是线段上的一个动点与、不重合),过点作平行于轴的直线交抛物线于点,交轴于点,设点的横坐标为,的面积为.
①求与的函数关系式;
②是否存在最大值?若存在,求出最大值及此时点的坐标; 若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数的实际应用-销售问题
2.【答案】C
【知识点】二次函数的实际应用-抛球问题
3.【答案】B
【知识点】二次函数的实际应用-销售问题
4.【答案】D
【知识点】二次函数的实际应用-百分率问题
5.【答案】D
【知识点】二次函数的实际应用-拱桥问题
6.【答案】A
【知识点】二次函数的实际应用-几何问题
7.【答案】B
【知识点】二次函数的实际应用-销售问题
8.【答案】A
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】A
【知识点】二次函数-动态几何问题
11.【答案】
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
12.【答案】
【知识点】二次函数的实际应用-销售问题
13.【答案】10
【知识点】二次函数的实际应用-抛球问题
14.【答案】(1)
(2)2450
【知识点】二次函数的实际应用-销售问题
15.【答案】20
【知识点】二次函数的实际应用-抛球问题
16.【答案】(1)4
(2)
【知识点】平行四边形的判定与性质;轴对称的应用-最短距离问题;二次函数与一次函数的综合应用;二次函数的其他应用
17.【答案】(1)
(2)当售价为12元时,每日获的利润最大,最大利润为720元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)米;(2)铅球推出的水平距离为10米;(3)铅球的行进高度不能达到4米
【知识点】二次函数的实际应用-抛球问题
19.【答案】解:(1)由题知点在抛物线上,
得,
解得,
∴,
∴当时,
∴抛物线解析式为,拱顶D到地面OA的距离为10米;
(2)可以通过,理由如下:
由题知车最外侧与地面OA的交点为(2,0)或(10,0)
当x=2或x=10时,,
所以可以通过;
(3)令,即,
可得,
解得
答:两排灯的水平距离最小是.
【知识点】二次函数的实际应用-拱桥问题
20.【答案】(1)1秒后四边形APQC的面积是19平方厘米
(2)时,取最小值为15平方厘米
【知识点】二次函数-动态几何问题
21.【答案】(1)
(2)当米时,水流不落在池外
【知识点】二次函数的实际应用-喷水问题
22.【答案】(1)12m或16m;(2)195m2.
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
23.【答案】(1).
(2)
(3)①
②当m=﹣2时,S最大,最大值为1,此时点E的坐标为(﹣2,2).
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
21.4 二次函数的应用
一、单选题
1.(2024九下·江阴模拟)某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
2.(2024九上·汉阳期中)如图,一名男生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,他推出铅球的距离为( )
A. B. C. D.
3.(2022九上·顺平期中)某书店销售某种中考复习资料,若每本可获利元,一天可售出本,则该书店出售该种中考复习资料的日利润最大为( )
A.250元 B.500元 C.750元 D.1000元
4.(2023九上·武汉月考)某超市一月份的营业额为万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,则根据题意列方程为( )
A. B.
C. D.
5.(2024九下·嘉禾期中)如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
6.(2022九下·定州模拟)某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的三处各留宽的门,所有围栏的总长(不含门)为,则能建成的饲养室面积最大为( )
A. B. C. D.
7.(2023九上·金安期中)某公司销售一种成本为每件20元的LED护眼台灯.销售过程中发现,若销售单价为x元,则月销售量为件.为使每月获得最大利润,该台灯应定价为( )
A.30元 B.35元 C.40元 D.45元
8.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
9.(2018九上·绍兴期中)已知如图,抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,垂足为Q,当∠ACH=∠CPQ时,此时CP的长为()
A. B. C. D.
10.(2020九上·霸州期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( )
A.①④ B.②④ C.①③ D.②③
二、填空题
11.(2023九上·招远期中)如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是,则选取点B为坐标原点时的抛物线表达式是 .
12.(2023九上·平邑月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出千克,经调查,售价每降元,每天多卖千克,另外,每天的其它固定成本元.当定价为 元能获得最大利润.
13.(2024九上·济宁月考)一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的函数关系式是,则他将铅球推出的距离是 m.
14.(2021九上·雄县)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为 ;
(2)日销售的最大利润为 元.
15.(2023·平凉模拟) 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则小球飞行最大高度是
16.(2023九上·上虞月考)如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
(1)如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .
(2)如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .
三、计算题
17.(2025·罗湖模拟)抖音直播购物逐渐走进了人们的生活.为提高我县特产红富士苹果的影响力,某电商在抖音平台上对我县红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可售出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.若想通过涨价增加每日利润,设涨价后的售价为元,每日获得的利润为元.
(1)涨价后每日销量将减少______件(用含的代数式表示);
(2)当售价为多少时,每日获的利润最大?最大利润为多少?
18.(2023九上·新会期中)一名男生推铅球,铅球的行进高度(单位:)与水平距离(单位:)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4.
19.(2024九上·大安期中)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
四、解答题
20.(2024九上·黑龙江期中)如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
(1)几秒后四边形APQC的面积是19平方厘米;
(2)若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.
21.(2023九上·杭州月考)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度与水平距离之间的关系式是.
(1)水流喷出的最大高度是多少?
(2)若不计其他因素,水池的半径至少为多少,才能使喷出的水流不落在池外?
22.(2025九上·门头沟期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
23.(2024九下·凉州期中)如图,已知抛物线经过,,三点,其顶点为,对称轴是直线,与轴交于点.
(1)求该抛物线的解析式;
(2)若点是该抛物线对称轴上的一个动点,求周长的最小值;
(3)如图(2),若是线段上的一个动点与、不重合),过点作平行于轴的直线交抛物线于点,交轴于点,设点的横坐标为,的面积为.
①求与的函数关系式;
②是否存在最大值?若存在,求出最大值及此时点的坐标; 若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数的实际应用-销售问题
2.【答案】C
【知识点】二次函数的实际应用-抛球问题
3.【答案】B
【知识点】二次函数的实际应用-销售问题
4.【答案】D
【知识点】二次函数的实际应用-百分率问题
5.【答案】D
【知识点】二次函数的实际应用-拱桥问题
6.【答案】A
【知识点】二次函数的实际应用-几何问题
7.【答案】B
【知识点】二次函数的实际应用-销售问题
8.【答案】A
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】A
【知识点】二次函数-动态几何问题
11.【答案】
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
12.【答案】
【知识点】二次函数的实际应用-销售问题
13.【答案】10
【知识点】二次函数的实际应用-抛球问题
14.【答案】(1)
(2)2450
【知识点】二次函数的实际应用-销售问题
15.【答案】20
【知识点】二次函数的实际应用-抛球问题
16.【答案】(1)4
(2)
【知识点】平行四边形的判定与性质;轴对称的应用-最短距离问题;二次函数与一次函数的综合应用;二次函数的其他应用
17.【答案】(1)
(2)当售价为12元时,每日获的利润最大,最大利润为720元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)米;(2)铅球推出的水平距离为10米;(3)铅球的行进高度不能达到4米
【知识点】二次函数的实际应用-抛球问题
19.【答案】解:(1)由题知点在抛物线上,
得,
解得,
∴,
∴当时,
∴抛物线解析式为,拱顶D到地面OA的距离为10米;
(2)可以通过,理由如下:
由题知车最外侧与地面OA的交点为(2,0)或(10,0)
当x=2或x=10时,,
所以可以通过;
(3)令,即,
可得,
解得
答:两排灯的水平距离最小是.
【知识点】二次函数的实际应用-拱桥问题
20.【答案】(1)1秒后四边形APQC的面积是19平方厘米
(2)时,取最小值为15平方厘米
【知识点】二次函数-动态几何问题
21.【答案】(1)
(2)当米时,水流不落在池外
【知识点】二次函数的实际应用-喷水问题
22.【答案】(1)12m或16m;(2)195m2.
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
23.【答案】(1).
(2)
(3)①
②当m=﹣2时,S最大,最大值为1,此时点E的坐标为(﹣2,2).
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
21.4 二次函数的应用
一、单选题
1.(2024九下·江阴模拟)某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
2.(2024九上·汉阳期中)如图,一名男生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,他推出铅球的距离为( )
A. B. C. D.
3.(2022九上·顺平期中)某书店销售某种中考复习资料,若每本可获利元,一天可售出本,则该书店出售该种中考复习资料的日利润最大为( )
A.250元 B.500元 C.750元 D.1000元
4.(2023九上·武汉月考)某超市一月份的营业额为万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,则根据题意列方程为( )
A. B.
C. D.
5.(2024九下·嘉禾期中)如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
6.(2022九下·定州模拟)某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的三处各留宽的门,所有围栏的总长(不含门)为,则能建成的饲养室面积最大为( )
A. B. C. D.
7.(2023九上·金安期中)某公司销售一种成本为每件20元的LED护眼台灯.销售过程中发现,若销售单价为x元,则月销售量为件.为使每月获得最大利润,该台灯应定价为( )
A.30元 B.35元 C.40元 D.45元
8.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
9.(2018九上·绍兴期中)已知如图,抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,垂足为Q,当∠ACH=∠CPQ时,此时CP的长为()
A. B. C. D.
10.(2020九上·霸州期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( )
A.①④ B.②④ C.①③ D.②③
二、填空题
11.(2023九上·招远期中)如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是,则选取点B为坐标原点时的抛物线表达式是 .
12.(2023九上·平邑月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出千克,经调查,售价每降元,每天多卖千克,另外,每天的其它固定成本元.当定价为 元能获得最大利润.
13.(2024九上·济宁月考)一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的函数关系式是,则他将铅球推出的距离是 m.
14.(2021九上·雄县)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为 ;
(2)日销售的最大利润为 元.
15.(2023·平凉模拟) 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则小球飞行最大高度是
16.(2023九上·上虞月考)如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
(1)如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .
(2)如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .
三、计算题
17.(2025·罗湖模拟)抖音直播购物逐渐走进了人们的生活.为提高我县特产红富士苹果的影响力,某电商在抖音平台上对我县红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可售出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.若想通过涨价增加每日利润,设涨价后的售价为元,每日获得的利润为元.
(1)涨价后每日销量将减少______件(用含的代数式表示);
(2)当售价为多少时,每日获的利润最大?最大利润为多少?
18.(2023九上·新会期中)一名男生推铅球,铅球的行进高度(单位:)与水平距离(单位:)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4.
19.(2024九上·大安期中)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
四、解答题
20.(2024九上·黑龙江期中)如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
(1)几秒后四边形APQC的面积是19平方厘米;
(2)若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.
21.(2023九上·杭州月考)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度与水平距离之间的关系式是.
(1)水流喷出的最大高度是多少?
(2)若不计其他因素,水池的半径至少为多少,才能使喷出的水流不落在池外?
22.(2025九上·门头沟期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
23.(2024九下·凉州期中)如图,已知抛物线经过,,三点,其顶点为,对称轴是直线,与轴交于点.
(1)求该抛物线的解析式;
(2)若点是该抛物线对称轴上的一个动点,求周长的最小值;
(3)如图(2),若是线段上的一个动点与、不重合),过点作平行于轴的直线交抛物线于点,交轴于点,设点的横坐标为,的面积为.
①求与的函数关系式;
②是否存在最大值?若存在,求出最大值及此时点的坐标; 若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数的实际应用-销售问题
2.【答案】C
【知识点】二次函数的实际应用-抛球问题
3.【答案】B
【知识点】二次函数的实际应用-销售问题
4.【答案】D
【知识点】二次函数的实际应用-百分率问题
5.【答案】D
【知识点】二次函数的实际应用-拱桥问题
6.【答案】A
【知识点】二次函数的实际应用-几何问题
7.【答案】B
【知识点】二次函数的实际应用-销售问题
8.【答案】A
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】A
【知识点】二次函数-动态几何问题
11.【答案】
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
12.【答案】
【知识点】二次函数的实际应用-销售问题
13.【答案】10
【知识点】二次函数的实际应用-抛球问题
14.【答案】(1)
(2)2450
【知识点】二次函数的实际应用-销售问题
15.【答案】20
【知识点】二次函数的实际应用-抛球问题
16.【答案】(1)4
(2)
【知识点】平行四边形的判定与性质;轴对称的应用-最短距离问题;二次函数与一次函数的综合应用;二次函数的其他应用
17.【答案】(1)
(2)当售价为12元时,每日获的利润最大,最大利润为720元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)米;(2)铅球推出的水平距离为10米;(3)铅球的行进高度不能达到4米
【知识点】二次函数的实际应用-抛球问题
19.【答案】解:(1)由题知点在抛物线上,
得,
解得,
∴,
∴当时,
∴抛物线解析式为,拱顶D到地面OA的距离为10米;
(2)可以通过,理由如下:
由题知车最外侧与地面OA的交点为(2,0)或(10,0)
当x=2或x=10时,,
所以可以通过;
(3)令,即,
可得,
解得
答:两排灯的水平距离最小是.
【知识点】二次函数的实际应用-拱桥问题
20.【答案】(1)1秒后四边形APQC的面积是19平方厘米
(2)时,取最小值为15平方厘米
【知识点】二次函数-动态几何问题
21.【答案】(1)
(2)当米时,水流不落在池外
【知识点】二次函数的实际应用-喷水问题
22.【答案】(1)12m或16m;(2)195m2.
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
23.【答案】(1).
(2)
(3)①
②当m=﹣2时,S最大,最大值为1,此时点E的坐标为(﹣2,2).
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
21.4 二次函数的应用
一、单选题
1.(2024九下·江阴模拟)某公司计划生产一种新型电子产品,经过公司测算,在生产数量不超过8万件的情况下,生产成本和销售价格均是生产数量的一次函数,其部分数据如下表:
生产数量(万件) 生产成本(元/件) 销售价格(元/件)
1 9 16
2 8 14
3 7 12
为获最大利润,生产数量应为( )
A.3万件 B.4万件 C.5万件 D.6万件
2.(2024九上·汉阳期中)如图,一名男生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是,他推出铅球的距离为( )
A. B. C. D.
3.(2022九上·顺平期中)某书店销售某种中考复习资料,若每本可获利元,一天可售出本,则该书店出售该种中考复习资料的日利润最大为( )
A.250元 B.500元 C.750元 D.1000元
4.(2023九上·武汉月考)某超市一月份的营业额为万元,一月、二月、三月的营业额共万元,如果平均每月增长率为,则根据题意列方程为( )
A. B.
C. D.
5.(2024九下·嘉禾期中)如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
6.(2022九下·定州模拟)某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图所示的三处各留宽的门,所有围栏的总长(不含门)为,则能建成的饲养室面积最大为( )
A. B. C. D.
7.(2023九上·金安期中)某公司销售一种成本为每件20元的LED护眼台灯.销售过程中发现,若销售单价为x元,则月销售量为件.为使每月获得最大利润,该台灯应定价为( )
A.30元 B.35元 C.40元 D.45元
8.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
9.(2018九上·绍兴期中)已知如图,抛物线y=-x2-2x+3交x轴于A、B两点,顶点为C,CH⊥AB交x轴于H,在CH右侧的抛物线上有一点P,已知PQ⊥AC,垂足为Q,当∠ACH=∠CPQ时,此时CP的长为()
A. B. C. D.
10.(2020九上·霸州期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿抛物线向点 匀速运动,到达点 停止,设运动时间为 秒,当 和 时, 的值相等.有下列结论:① 时, 的值最大;② 时,点 停止运动;③当 和 时, 的值不相等;④ 时, .其中正确的是( )
A.①④ B.②④ C.①③ D.②③
二、填空题
11.(2023九上·招远期中)如图的一座拱桥,当水面宽为时,桥洞顶部离水面,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线表达式是,则选取点B为坐标原点时的抛物线表达式是 .
12.(2023九上·平邑月考)某西瓜经营户以2元/千克的价格购进一批西瓜,以3元/千克售出,每天可售出千克,经调查,售价每降元,每天多卖千克,另外,每天的其它固定成本元.当定价为 元能获得最大利润.
13.(2024九上·济宁月考)一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的函数关系式是,则他将铅球推出的距离是 m.
14.(2021九上·雄县)某公司经过市场调查,整理出某种商品在某个月的第x天与日销售量的相关信息如下表所示.已知商品的进价为20元/件,设该商品的日销售利润为y元.
第x天 售价(元/件) 日销售量件
(1)y与x的函数解析式为 ;
(2)日销售的最大利润为 元.
15.(2023·平凉模拟) 如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线若不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系:,则小球飞行最大高度是
16.(2023九上·上虞月考)如图①,是一建筑物造型的纵截面,曲线OBA是抛物线的一部分,该抛物线开口向右、对称轴正好是水平线OH,AC,BD是与水平线OH垂直的两根支柱,AC=4米,BD=2米,OD=2米.
(1)如图②,为了安全美观,准备拆除支柱AC、BD,在水平线OH上另找一点P作为地面上的支撑点,用固定材料连接PA、PB,对抛物线造型进行支撑加固,用料最省时点O,P之间的距离是 .
(2)如图③,在水平线OH上增添一张2米长的椅子EF(E在F右侧),用固定材料连接AE、BF,对抛物线造型进行支撑加固,用料最省时点O,E之间的距离是 .
三、计算题
17.(2025·罗湖模拟)抖音直播购物逐渐走进了人们的生活.为提高我县特产红富士苹果的影响力,某电商在抖音平台上对我县红富士苹果进行直播销售.已知苹果的成本价为6元/千克,如果按10元/千克销售,每天可售出160千克.通过调查发现,每千克苹果售价增加1元,日销售量减少20千克.若想通过涨价增加每日利润,设涨价后的售价为元,每日获得的利润为元.
(1)涨价后每日销量将减少______件(用含的代数式表示);
(2)当售价为多少时,每日获的利润最大?最大利润为多少?
18.(2023九上·新会期中)一名男生推铅球,铅球的行进高度(单位:)与水平距离(单位:)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4.
19.(2024九上·大安期中)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
四、解答题
20.(2024九上·黑龙江期中)如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
(1)几秒后四边形APQC的面积是19平方厘米;
(2)若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.
21.(2023九上·杭州月考)如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置,处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度与水平距离之间的关系式是.
(1)水流喷出的最大高度是多少?
(2)若不计其他因素,水池的半径至少为多少,才能使喷出的水流不落在池外?
22.(2025九上·门头沟期末)在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
23.(2024九下·凉州期中)如图,已知抛物线经过,,三点,其顶点为,对称轴是直线,与轴交于点.
(1)求该抛物线的解析式;
(2)若点是该抛物线对称轴上的一个动点,求周长的最小值;
(3)如图(2),若是线段上的一个动点与、不重合),过点作平行于轴的直线交抛物线于点,交轴于点,设点的横坐标为,的面积为.
①求与的函数关系式;
②是否存在最大值?若存在,求出最大值及此时点的坐标; 若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】二次函数的实际应用-销售问题
2.【答案】C
【知识点】二次函数的实际应用-抛球问题
3.【答案】B
【知识点】二次函数的实际应用-销售问题
4.【答案】D
【知识点】二次函数的实际应用-百分率问题
5.【答案】D
【知识点】二次函数的实际应用-拱桥问题
6.【答案】A
【知识点】二次函数的实际应用-几何问题
7.【答案】B
【知识点】二次函数的实际应用-销售问题
8.【答案】A
【知识点】二次函数的实际应用-几何问题
9.【答案】D
【知识点】二次函数的实际应用-几何问题
10.【答案】A
【知识点】二次函数-动态几何问题
11.【答案】
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-拱桥问题
12.【答案】
【知识点】二次函数的实际应用-销售问题
13.【答案】10
【知识点】二次函数的实际应用-抛球问题
14.【答案】(1)
(2)2450
【知识点】二次函数的实际应用-销售问题
15.【答案】20
【知识点】二次函数的实际应用-抛球问题
16.【答案】(1)4
(2)
【知识点】平行四边形的判定与性质;轴对称的应用-最短距离问题;二次函数与一次函数的综合应用;二次函数的其他应用
17.【答案】(1)
(2)当售价为12元时,每日获的利润最大,最大利润为720元
【知识点】二次函数的最值;二次函数的实际应用-销售问题
18.【答案】(1)米;(2)铅球推出的水平距离为10米;(3)铅球的行进高度不能达到4米
【知识点】二次函数的实际应用-抛球问题
19.【答案】解:(1)由题知点在抛物线上,
得,
解得,
∴,
∴当时,
∴抛物线解析式为,拱顶D到地面OA的距离为10米;
(2)可以通过,理由如下:
由题知车最外侧与地面OA的交点为(2,0)或(10,0)
当x=2或x=10时,,
所以可以通过;
(3)令,即,
可得,
解得
答:两排灯的水平距离最小是.
【知识点】二次函数的实际应用-拱桥问题
20.【答案】(1)1秒后四边形APQC的面积是19平方厘米
(2)时,取最小值为15平方厘米
【知识点】二次函数-动态几何问题
21.【答案】(1)
(2)当米时,水流不落在池外
【知识点】二次函数的实际应用-喷水问题
22.【答案】(1)12m或16m;(2)195m2.
【知识点】一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
23.【答案】(1).
(2)
(3)①
②当m=﹣2时,S最大,最大值为1,此时点E的坐标为(﹣2,2).
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
