2024-2025学年江苏省扬州中学树人教育集团七年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年江苏省扬州中学树人教育集团七年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 15:15:52 | ||
图片预览




文档简介
2024-2025学年江苏省扬州中学树人教育集团七年级(下)期末数学试卷
一、选择题(共8小题,每题3分,共24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(3分)若(3×3×3×3)m=92,则m的值为( )
A.1 B.2 C.3 D.4
3.(3分)如果a>b,则下列结论一定正确的是( )
A.﹣2a>﹣2b B. C.2﹣a>2﹣b D.a﹣2>b﹣2
4.(3分)若(x2+ax+2)(2x﹣4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.﹣2
5.(3分)下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.若a2>b2,则a>b
C.如果a2=b2,那么a=b
D.对顶角相等
6.(3分)若a+b=﹣4,ab=﹣2,则(a﹣b)2=( )
A.8 B.12 C.16 D.24
7.(3分)如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
8.(3分)式子2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381,则log381=4,同理log327=3,log33=1.由此可以得到下列式子:log381=log3(27×3)=log327+log33,且若logab=logac,则b=c,根据以上的信息及运关系,若log4(x+12)+log4x=2log4(x+2),则x=( )
A. B. C.7 D.
二、填空题(共10小题,每题3分,共30分)
9.(3分)中国科研团队突破性研制全球最薄金属材料,材料的厚度仅为0.00000000058m,是头发丝的二十万分之一.将0.00000000058用科学记数法表示为 .
10.(3分)若3a=4,3b=2,则3a﹣b= .
11.(3分)已知某多边形的每个外角都等于36°,则这个多边形是 边形.
12.(3分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 .
13.(3分)若x2﹣3(k+1)x+36是一个完全平方式,则k= .
14.(3分)若关于x,y的方程组的解满足3x﹣y≤1,则m的最大整数解为 .
15.(3分)用反证法证明“三角形中必有一个内角不大于60°”时,应假设 .
16.(3分)如图,在4×4的正方形网格中有三个黑色正方形,请你在网格中再涂黑一个小正方形,使其与原有的黑色正方形构成一个中心对称图形,则可供选择的白色小正方形的个数为 .
17.(3分)设a1,a2,…,a2025是从﹣1,0,1这三个数中取值的一列数,若a1+a2+ +a2025=0,(a1+1)2+(a2+1)2+ +(a2025+1)2=3025,则a1,a2,…,a2025中值为﹣1或0的个数共有 个.
18.(3分)如图,在△AOB在和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,OD与OA重叠.若△AOB绕点O按每秒20°的速度沿逆时针方向旋转不停,在旋转过程中,若△AOB和△COD中第一次有一组边平行,则称之为第一次“边平行”,当旋转到 秒时,第2025次边平行.
三.解答题(共10小题,共96分)
19.(8分)计算:
(1);
(2)a a5﹣(2a3)2+a9÷a3.
20.(8分)(1)解方程组:;
(2)解不等式组:,并用数轴表示解集.
21.(8分)先化简,再求值:(x﹣y)(x+y)﹣(y﹣4)2+x(y﹣x),其中.
22.(8分)如图,在边长为1的小正方形组成的网格中,将△ABC平移得到△A′B′C′,连接AA′,BB′.
(1)根据题意,补全图形;
(2)线段AA′与线段BB′之间的位置关系和数量关系是 ;
(3)在BB′上画出一点P,使得∠PA′B′=∠ABC.
23.(10分)定义:任意两个数a,b,按规则c=(a+1)(b+1)运算得到一个新数c,称所得的新数c为a,b的“和积数”.
(1)若a=4,b=﹣2,求a,b的“和积数”c;
(2)若,求a,b的“和积数”c.
24.(10分)如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
25.(10分)如图,在△ABC中,∠C=90°,∠A=30°,请用无刻度直尺和圆规作图.(标注字母,保留作图痕迹,不要求写作法)
(1)图①,在边AC上找一点D,使得∠BDC=60°;
(2)图②,E是AB上一点,在边AC上作点F,使∠EFC=2∠A.
26.(10分)某奶茶店推出A、B两款新品奶茶,已知购买5杯A奶茶和4杯B奶茶共花费130元,购买3杯A奶茶和2杯B奶茶共花费72元.
(1)求A、B两款奶茶的单价各为多少元?
(2)某班参加社会实践活动的有56位学生和4名教师,现该班决定团购下午茶,恰逢A、B两款新品奶茶搞促销活动,其中A奶茶在原来单价的基础上优惠5元,B奶茶在原来单价的基础上打八折,在班级现有经费648元的情况下,若B奶茶的数量不少于34杯,且所有参加活动的师生均有下午茶享用,则共有哪几种购买方案?哪种方案花费最少?最少费用多少元?
27.(12分)若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
例如,方程x﹣1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x﹣1=3是不等式组的“关联方程”.
(1)请判断,方程3(x+1)﹣x=9 (“是”或“不是”)不等式组的“关联方程”;
(2)若关于x的方程2x﹣k=6是不等式组的“关联方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“关联方程”.且此时不等式组有4个整数解,试求m的取值范围.
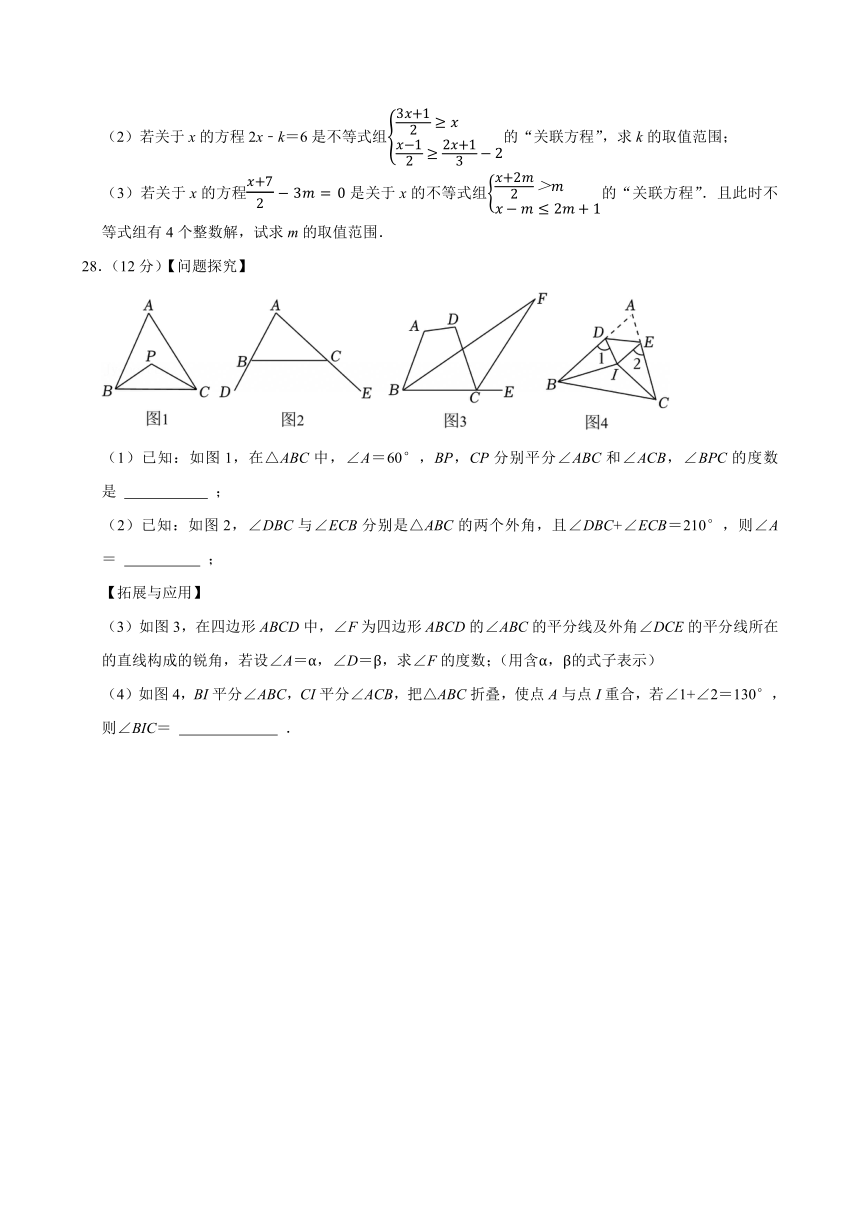
28.(12分)【问题探究】
(1)已知:如图1,在△ABC中,∠A=60°,BP,CP分别平分∠ABC和∠ACB,∠BPC的度数是 ;
(2)已知:如图2,∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,则∠A= ;
【拓展与应用】
(3)如图3,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β,求∠F的度数;(用含α,β的式子表示)
(4)如图4,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,则∠BIC= .
2024-2025学年江苏省扬州中学树人教育集团七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A D B C D A A
一、选择题(共8小题,每题3分,共24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形但是中心对称图形,故不符合题意;
B、是轴对称图形但不是中心对称图形,故不符合题意;
C、既不是轴对称图形也不是中心对称图形,故不符合题意;
D、既是轴对称图形也是中心对称图形,故符合题意;
故选:D.
2.(3分)若(3×3×3×3)m=92,则m的值为( )
A.1 B.2 C.3 D.4
【解答】解:由条件可得(34)m=(32)2,
34m=34,
即4m=4,
∴m=1.
故选:A.
3.(3分)如果a>b,则下列结论一定正确的是( )
A.﹣2a>﹣2b B. C.2﹣a>2﹣b D.a﹣2>b﹣2
【解答】解:A、∵a>b,∴﹣2a<﹣2b,不符合题意,选项错误;
B、∵a>b,∴,不符合题意,选项错误;
C、∵a>b,∴﹣a<﹣b,∴2﹣a<2﹣b,不符合题意,选项错误;
D、∵a>b,∴a﹣2>b﹣2,符合题意,选项正确;
故选:D.
4.(3分)若(x2+ax+2)(2x﹣4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.﹣2
【解答】解:(x2+ax+2)(2x﹣4)
=2x3﹣4x2+2ax2﹣4ax+4x﹣8
=2x3+(2a﹣4)x2+(4﹣4a)x﹣8,
∵结果中不含x2项,
∴2a﹣4=0,
∴a=2,
故选:B.
5.(3分)下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.若a2>b2,则a>b
C.如果a2=b2,那么a=b
D.对顶角相等
【解答】解:A、如果两个角是直角,那么它们相等,逆命题是如果两个角相等,那么这两个角是直角,逆命题是假命题,不符合题意;
B、若a2>b2,则a>b,逆命题是若a>b,则a2>b2,逆命题是假命题,不符合题意;
C、如果a2=b2,那么a=b,逆命题是如果a=b,那么a2=b2,逆命题是真命题,符合题意;
D、对顶角相等,逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
故选:C.
6.(3分)若a+b=﹣4,ab=﹣2,则(a﹣b)2=( )
A.8 B.12 C.16 D.24
【解答】解:∵a+b=﹣4,ab=﹣2,
∴(a﹣b)2
=(a+b)2﹣4ab
=(﹣4)2﹣4×(﹣2)
=16+8
=24,
故选:D.
7.(3分)如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解.
【解答】解:如图,过点A作l1的平行线AC,过点B作l2的平行线BD,
则∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选:A.
8.(3分)式子2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381,则log381=4,同理log327=3,log33=1.由此可以得到下列式子:log381=log3(27×3)=log327+log33,且若logab=logac,则b=c,根据以上的信息及运关系,若log4(x+12)+log4x=2log4(x+2),则x=( )
A. B. C.7 D.
【解答】解:设a=log3(x+12),b=log3x,c=log3(x+2),
∴3a+b=x(x+12),32c=(x+2) (x+2)=(x+2)2,
∴a+b=log3x(x+12),,
∴,
∴x(x+12)=(x+2)2,
解得:.
故选:A.
二、填空题(共10小题,每题3分,共30分)
9.(3分)中国科研团队突破性研制全球最薄金属材料,材料的厚度仅为0.00000000058m,是头发丝的二十万分之一.将0.00000000058用科学记数法表示为 5.8×10﹣10 .
【解答】解:0.00000000058=5.8×10﹣10.
故答案为:5.8×10﹣10.
10.(3分)若3a=4,3b=2,则3a﹣b= 2 .
【解答】解:由条件可得3a﹣b=3a÷3b=4÷2=2;
故答案为:2.
11.(3分)已知某多边形的每个外角都等于36°,则这个多边形是 10 边形.
【解答】解:∵这个多边形的每个外角都等于36°,
∴这个多边形的边数是:360÷36=10,
故答案为:10.
12.(3分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 2 .
【解答】解:∵(a+2)x|a|﹣1+y=5是一个二元一次方程,
∴,
解得:a=2,
故答案为:2.
13.(3分)若x2﹣3(k+1)x+36是一个完全平方式,则k= 3或﹣5 .
【解答】解:由条件可得﹣3(k+1)x=±2×6x,
∴k+1=4或k+1=﹣4,
解得k=3或k=﹣5,
故答案为:3或﹣5.
14.(3分)若关于x,y的方程组的解满足3x﹣y≤1,则m的最大整数解为 0 .
【解答】解:,
①+②得:3x﹣y=3m+1,
∵关于x,y的方程组的解满足3x﹣y≤1,
∴3m+1≤1,
∴m≤0,
∴m的最大整数解为0,
故答案为:0.
15.(3分)用反证法证明“三角形中必有一个内角不大于60°”时,应假设 每一个内角都大于60° .
【解答】解:根据反证法可知:每一个内角都大于60°.
故答案为:每一个内角都大于60°.
16.(3分)如图,在4×4的正方形网格中有三个黑色正方形,请你在网格中再涂黑一个小正方形,使其与原有的黑色正方形构成一个中心对称图形,则可供选择的白色小正方形的个数为 3 .
【解答】解:如图所示:标有数字的3个位置都是中心对称图形.
故答案为:3.
17.(3分)设a1,a2,…,a2025是从﹣1,0,1这三个数中取值的一列数,若a1+a2+ +a2025=0,(a1+1)2+(a2+1)2+ +(a2025+1)2=3025,则a1,a2,…,a2025中值为﹣1或0的个数共有 1525 个.
【解答】解:设值为﹣1、0、1的个数分别为x、y、z,
根据题意:,
解得:x=500,y=1025,z=500.
∴值为﹣1或0的个数为x+y=1525.
故答案为:1525.
18.(3分)如图,在△AOB在和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,OD与OA重叠.若△AOB绕点O按每秒20°的速度沿逆时针方向旋转不停,在旋转过程中,若△AOB和△COD中第一次有一组边平行,则称之为第一次“边平行”,当旋转到 3643.5 秒时,第2025次边平行.
【解答】解:在△AOB和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,
∴∠CDO=30°,∠ABO=50°如图,第1次边平行时,AB∥CO,
∴∠COB=180°﹣∠ABO=130°,
∴旋转了180°﹣130°=50°,旋转2.5(秒),
如图,第2次边平行时,CD∥BO,
∴∠BOD=∠D=30°,
∴旋转了90°﹣30°=60°,旋转3(秒),
如图,第3次边平行时,AC∥BD,设OB,CD交于点E,
∴∠DEB=∠ABO=50°,
∴∠BOD=∠BED﹣∠CDO=50°﹣30°=20°,
∴旋转了20°+90°=110°,旋转了5.5(秒),
如图,第4次边平行时,AB∥DO,
∴∠BOD=∠ABO=50°,
∴旋转了90°+50°=140°,旋转时间为7(秒),
如图,第5次边平行时,CD∥AO,
∴∠AOC=∠C=60°,
∴∠BOC=90°﹣∠AOC=30°,
∴∠BOD=90°﹣∠BOC=60°,
∴旋转了90°+60°=150°,旋转时间为7.5(秒),
如图,第6次边平行时,CO∥AB,
∵∠BOC=∠ABO=50°,
∴旋转了180°+50°=230°,旋转时间为11.5(秒),
如图,第7次边平行时,CD∥BO,
∴∠BOC=∠C=60°,
∴旋转了180°+60°=240°,
旋转时间为12(秒),
如图,第8次边平行时,CD∥AB,设直线OB交CD于点F,
∴∠DFO=180°﹣∠B=130°,
∴∠DOF=180°﹣130°﹣30°﹣20°,
∴旋转了180°+20°+90°=290°,
旋转时间为14.5(秒),
如图,第9次边平行时,OD∥AB,
∴∠AOD=∠BAO=40°,
∴旋转了360°﹣40°=320°,
旋转时间为16(秒),
如图,第10次边平行时,CD∥AO,
∠AOD=∠CDO=30°,
∴旋转了360°﹣30°=330°,
旋转时间为15.5 (秒),再旋转30°就回到初始位置,
∴△OAB旋转1周有10次边平行,旋转时间为18(秒),
∵2025÷10=202…5,
第2025次平行时,旋转了202周,再加7.5秒,
∴202×18+7.5=3643.5,
故答案为:3643.5.
三.解答题(共10小题,共96分)
19.(8分)计算:
(1);
(2)a a5﹣(2a3)2+a9÷a3.
【解答】解:(1)
=﹣1+3+1﹣8
=﹣5;
(2)a a5﹣(2a3)2+a9÷a3
=a6﹣4a6+a6
=﹣2a6.
20.(8分)(1)解方程组:;
(2)解不等式组:,并用数轴表示解集.
【解答】解:(1),
①×2+③得,7x=14,
解得x=2,
把x=2代入②得,2+4y=4,
解得y,
所以原方程组的解为;
(2),
解不等式①得,x<2,
解不等式②得,x≥﹣1,
把两个不等式的解集在数轴上表示为:
所以不等式组的解集为﹣1≤x<2.
21.(8分)先化简,再求值:(x﹣y)(x+y)﹣(y﹣4)2+x(y﹣x),其中.
【解答】解:原式=x2﹣y2﹣(y2﹣8y+16)+xy﹣x2
=x2﹣y2﹣y2+8y﹣16+xy﹣x2
=﹣2y2+8y﹣16+xy.
当时,原式=﹣8+16﹣16+1=﹣7.
22.(8分)如图,在边长为1的小正方形组成的网格中,将△ABC平移得到△A′B′C′,连接AA′,BB′.
(1)根据题意,补全图形;
(2)线段AA′与线段BB′之间的位置关系和数量关系是 AA'∥BB',AA'=BB' ;
(3)在BB′上画出一点P,使得∠PA′B′=∠ABC.
【解答】解:(1)如图所示.
(2)由题意得,线段AA′与线段BB′之间的位置关系和数量关系是AA'∥BB',AA'=BB'.
故答案为:AA'∥BB',AA'=BB'.
(3)如图,过点A'作B'C'的平行线,交BB'于点P,
∴∠PA′B′=∠A'B'C',
由平移得∠A'B'C'=∠ABC,
∴∠PA′B′=∠ABC,
则点P即为所求.
23.(10分)定义:任意两个数a,b,按规则c=(a+1)(b+1)运算得到一个新数c,称所得的新数c为a,b的“和积数”.
(1)若a=4,b=﹣2,求a,b的“和积数”c;
(2)若,求a,b的“和积数”c.
【解答】解:(1)c=(4+1)(﹣2+1)=﹣5;
(2)c=(a+1)(b+1)=ab+a+b+1,
由条件可知(a+b)2=a2+b2+2ab=8+1=9,
∴a+b=3或a+b=﹣3,
当a+b=3时,,
当a+b=﹣3时,,
综上所述:c得值为或.
24.(10分)如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
【解答】解:(1)∠AED+∠D=180°;
∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠D=∠BED,
∴∠AED+∠D=180°;
(2)∵∠DHG=∠EHF=70°,∠D=30°,
∴∠HGD=80°,
∴∠CGF=180°﹣80°=100°,
∵CE∥GF,
∴∠C=180°﹣∠CGF=180°﹣100°=80°,
∵AB∥CD,
∴∠AEC=∠C=80°,
∴∠AEM=180°﹣∠AEC=180°﹣80°=100°.
25.(10分)如图,在△ABC中,∠C=90°,∠A=30°,请用无刻度直尺和圆规作图.(标注字母,保留作图痕迹,不要求写作法)
(1)图①,在边AC上找一点D,使得∠BDC=60°;
(2)图②,E是AB上一点,在边AC上作点F,使∠EFC=2∠A.
【解答】解:(1)如图①,作线段AB的垂直平分线,交AC于点D,
则AD=BD,
∴∠ABD=∠A=30°,
∴∠BDC=∠ABD+∠A=60°,
则点D即为所求.
(2)如图②,作线段AE的垂直平分线,交AC于点F,
则AF=EF,
∴∠AEF=∠A,
∴∠EFC=∠AEF+∠A=2∠A,
则点F即为所求.
26.(10分)某奶茶店推出A、B两款新品奶茶,已知购买5杯A奶茶和4杯B奶茶共花费130元,购买3杯A奶茶和2杯B奶茶共花费72元.
(1)求A、B两款奶茶的单价各为多少元?
(2)某班参加社会实践活动的有56位学生和4名教师,现该班决定团购下午茶,恰逢A、B两款新品奶茶搞促销活动,其中A奶茶在原来单价的基础上优惠5元,B奶茶在原来单价的基础上打八折,在班级现有经费648元的情况下,若B奶茶的数量不少于34杯,且所有参加活动的师生均有下午茶享用,则共有哪几种购买方案?哪种方案花费最少?最少费用多少元?
【解答】解:(1)设A款奶茶的单价为x元,B款奶茶的单价为y元,
根据题意得:,
解得:,
答:A款奶茶的单价为14元,B款奶茶的单价为15元;
(2)设购买A宽奶茶m杯,则购买B宽奶茶(60﹣m)杯,
根据题意得:,
解得:24≤m≤26,
∵m为正整数,
∴m可以为24,25,26,
∴共有3种购买方案:
①购买A奶茶24杯,购买B奶茶36杯,花费(14﹣5)×24+15×0.8×36=648(元);
②购买A奶茶25杯,购买B奶茶35杯,花费(14﹣5)×25+15×0.8×35=645(元);
③购买A奶茶26杯,购买B奶茶34杯,花费(14﹣5)×26+15×0.8×34=642(元);
∵648>645>642,
∴购买A奶茶26杯,购买B奶茶34杯最少,最少费用为642元,
答:共有3种购买方案,①购买A奶茶24杯,购买B奶茶36杯;②购买A奶茶25杯,购买B奶茶35杯;③购买A奶茶26杯,购买B奶茶34杯;购买A奶茶26杯,购买B奶茶34杯最少,最少费用为642元.
27.(12分)若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
例如,方程x﹣1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x﹣1=3是不等式组的“关联方程”.
(1)请判断,方程3(x+1)﹣x=9 是 (“是”或“不是”)不等式组的“关联方程”;
(2)若关于x的方程2x﹣k=6是不等式组的“关联方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“关联方程”.且此时不等式组有4个整数解,试求m的取值范围.
【解答】解:(1)由题意,∵3(x+1)﹣x=9,
∴x=3.
又∵不等式组为,
∴1<x≤5.
∴方程3(x+1)﹣x=9是不等式组的“关联方程”.
故答案为:是.
(2)由题意,∵2x﹣k=6,
∴x.
又∵不等式组为,
∴﹣1≤x≤7.
∴﹣17.
∴﹣8≤k≤8.
(3)由题意,∵,
∴x=6m﹣7.
又由不等式组,
∴解不等式①得:x>0,解不等式②得:x≤3m+1,
∴原不等式组的解集为:0<x≤3m+1,
∵不等式组有4个整数解,
∴整数的值为1,2,3,4,
∴4≤3m+1<5.
∴.
∵关于x的方程是关于x的不等式组的“关联方程”,
∴.
∴.
∴m的取值范围是.
28.(12分)【问题探究】
(1)已知:如图1,在△ABC中,∠A=60°,BP,CP分别平分∠ABC和∠ACB,∠BPC的度数是 120° ;
(2)已知:如图2,∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,则∠A= 30° ;
【拓展与应用】
(3)如图3,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β,求∠F的度数;(用含α,β的式子表示)
(4)如图4,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,则∠BIC= 122.5° .
【解答】解:(1)在△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵BP,CP分别平分∠ABC和∠ACB,
∴,,
∴,
∴∠BPC=180°﹣(∠PBC+∠PCB)=120°;
故答案为:120°;
(2)∵∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,
∴∠ABC+∠ACB=180°+180°﹣(∠DBC+∠ECB)=360°﹣210°=150°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣150°=30°;
故答案为:30°;
(3)延长BA,CD交于点Q,
∵∠BAD=α,∠ADC=β,同(2)可得∠Q=α+β﹣180°,
∵∠F为四边形ABCD的∠ABC 的平分线及外角∠DCE的平分线所在的直线构成的锐角,
∴,,
∵∠DCE=∠QBC+∠Q,∠FCE=∠FBC+∠F,
∴∠Q=∠DCE﹣∠QBC,2∠F=2∠FCE﹣2∠FBC=∠DCE﹣∠QBC,
∴∠Q=2∠F,
∴,
(4)∵∠1+∠2=130°,结合折叠,
∴∠ADI+AEI=180°+180°﹣(∠1+∠2)=230°,∠A=∠DIE,
∴65°,
∵BI平分∠ABC,CI平分∠ACB,
由(1)得:90°+32.5°=122.5°.
故答案为:122.5°.
一、选择题(共8小题,每题3分,共24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.(3分)若(3×3×3×3)m=92,则m的值为( )
A.1 B.2 C.3 D.4
3.(3分)如果a>b,则下列结论一定正确的是( )
A.﹣2a>﹣2b B. C.2﹣a>2﹣b D.a﹣2>b﹣2
4.(3分)若(x2+ax+2)(2x﹣4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.﹣2
5.(3分)下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.若a2>b2,则a>b
C.如果a2=b2,那么a=b
D.对顶角相等
6.(3分)若a+b=﹣4,ab=﹣2,则(a﹣b)2=( )
A.8 B.12 C.16 D.24
7.(3分)如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
8.(3分)式子2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381,则log381=4,同理log327=3,log33=1.由此可以得到下列式子:log381=log3(27×3)=log327+log33,且若logab=logac,则b=c,根据以上的信息及运关系,若log4(x+12)+log4x=2log4(x+2),则x=( )
A. B. C.7 D.
二、填空题(共10小题,每题3分,共30分)
9.(3分)中国科研团队突破性研制全球最薄金属材料,材料的厚度仅为0.00000000058m,是头发丝的二十万分之一.将0.00000000058用科学记数法表示为 .
10.(3分)若3a=4,3b=2,则3a﹣b= .
11.(3分)已知某多边形的每个外角都等于36°,则这个多边形是 边形.
12.(3分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 .
13.(3分)若x2﹣3(k+1)x+36是一个完全平方式,则k= .
14.(3分)若关于x,y的方程组的解满足3x﹣y≤1,则m的最大整数解为 .
15.(3分)用反证法证明“三角形中必有一个内角不大于60°”时,应假设 .
16.(3分)如图,在4×4的正方形网格中有三个黑色正方形,请你在网格中再涂黑一个小正方形,使其与原有的黑色正方形构成一个中心对称图形,则可供选择的白色小正方形的个数为 .
17.(3分)设a1,a2,…,a2025是从﹣1,0,1这三个数中取值的一列数,若a1+a2+ +a2025=0,(a1+1)2+(a2+1)2+ +(a2025+1)2=3025,则a1,a2,…,a2025中值为﹣1或0的个数共有 个.
18.(3分)如图,在△AOB在和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,OD与OA重叠.若△AOB绕点O按每秒20°的速度沿逆时针方向旋转不停,在旋转过程中,若△AOB和△COD中第一次有一组边平行,则称之为第一次“边平行”,当旋转到 秒时,第2025次边平行.
三.解答题(共10小题,共96分)
19.(8分)计算:
(1);
(2)a a5﹣(2a3)2+a9÷a3.
20.(8分)(1)解方程组:;
(2)解不等式组:,并用数轴表示解集.
21.(8分)先化简,再求值:(x﹣y)(x+y)﹣(y﹣4)2+x(y﹣x),其中.
22.(8分)如图,在边长为1的小正方形组成的网格中,将△ABC平移得到△A′B′C′,连接AA′,BB′.
(1)根据题意,补全图形;
(2)线段AA′与线段BB′之间的位置关系和数量关系是 ;
(3)在BB′上画出一点P,使得∠PA′B′=∠ABC.
23.(10分)定义:任意两个数a,b,按规则c=(a+1)(b+1)运算得到一个新数c,称所得的新数c为a,b的“和积数”.
(1)若a=4,b=﹣2,求a,b的“和积数”c;
(2)若,求a,b的“和积数”c.
24.(10分)如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
25.(10分)如图,在△ABC中,∠C=90°,∠A=30°,请用无刻度直尺和圆规作图.(标注字母,保留作图痕迹,不要求写作法)
(1)图①,在边AC上找一点D,使得∠BDC=60°;
(2)图②,E是AB上一点,在边AC上作点F,使∠EFC=2∠A.
26.(10分)某奶茶店推出A、B两款新品奶茶,已知购买5杯A奶茶和4杯B奶茶共花费130元,购买3杯A奶茶和2杯B奶茶共花费72元.
(1)求A、B两款奶茶的单价各为多少元?
(2)某班参加社会实践活动的有56位学生和4名教师,现该班决定团购下午茶,恰逢A、B两款新品奶茶搞促销活动,其中A奶茶在原来单价的基础上优惠5元,B奶茶在原来单价的基础上打八折,在班级现有经费648元的情况下,若B奶茶的数量不少于34杯,且所有参加活动的师生均有下午茶享用,则共有哪几种购买方案?哪种方案花费最少?最少费用多少元?
27.(12分)若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
例如,方程x﹣1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x﹣1=3是不等式组的“关联方程”.
(1)请判断,方程3(x+1)﹣x=9 (“是”或“不是”)不等式组的“关联方程”;
(2)若关于x的方程2x﹣k=6是不等式组的“关联方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“关联方程”.且此时不等式组有4个整数解,试求m的取值范围.
28.(12分)【问题探究】
(1)已知:如图1,在△ABC中,∠A=60°,BP,CP分别平分∠ABC和∠ACB,∠BPC的度数是 ;
(2)已知:如图2,∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,则∠A= ;
【拓展与应用】
(3)如图3,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β,求∠F的度数;(用含α,β的式子表示)
(4)如图4,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,则∠BIC= .
2024-2025学年江苏省扬州中学树人教育集团七年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A D B C D A A
一、选择题(共8小题,每题3分,共24分)
1.(3分)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形但是中心对称图形,故不符合题意;
B、是轴对称图形但不是中心对称图形,故不符合题意;
C、既不是轴对称图形也不是中心对称图形,故不符合题意;
D、既是轴对称图形也是中心对称图形,故符合题意;
故选:D.
2.(3分)若(3×3×3×3)m=92,则m的值为( )
A.1 B.2 C.3 D.4
【解答】解:由条件可得(34)m=(32)2,
34m=34,
即4m=4,
∴m=1.
故选:A.
3.(3分)如果a>b,则下列结论一定正确的是( )
A.﹣2a>﹣2b B. C.2﹣a>2﹣b D.a﹣2>b﹣2
【解答】解:A、∵a>b,∴﹣2a<﹣2b,不符合题意,选项错误;
B、∵a>b,∴,不符合题意,选项错误;
C、∵a>b,∴﹣a<﹣b,∴2﹣a<2﹣b,不符合题意,选项错误;
D、∵a>b,∴a﹣2>b﹣2,符合题意,选项正确;
故选:D.
4.(3分)若(x2+ax+2)(2x﹣4)的结果中不含x2项,则a的值为( )
A.0 B.2 C. D.﹣2
【解答】解:(x2+ax+2)(2x﹣4)
=2x3﹣4x2+2ax2﹣4ax+4x﹣8
=2x3+(2a﹣4)x2+(4﹣4a)x﹣8,
∵结果中不含x2项,
∴2a﹣4=0,
∴a=2,
故选:B.
5.(3分)下列命题的逆命题是真命题的是( )
A.如果两个角是直角,那么它们相等
B.若a2>b2,则a>b
C.如果a2=b2,那么a=b
D.对顶角相等
【解答】解:A、如果两个角是直角,那么它们相等,逆命题是如果两个角相等,那么这两个角是直角,逆命题是假命题,不符合题意;
B、若a2>b2,则a>b,逆命题是若a>b,则a2>b2,逆命题是假命题,不符合题意;
C、如果a2=b2,那么a=b,逆命题是如果a=b,那么a2=b2,逆命题是真命题,符合题意;
D、对顶角相等,逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
故选:C.
6.(3分)若a+b=﹣4,ab=﹣2,则(a﹣b)2=( )
A.8 B.12 C.16 D.24
【解答】解:∵a+b=﹣4,ab=﹣2,
∴(a﹣b)2
=(a+b)2﹣4ab
=(﹣4)2﹣4×(﹣2)
=16+8
=24,
故选:D.
7.(3分)如图,直线CE∥DF,∠CAB=125°,∠ABD=85°,则∠1+∠2=( )
A.30° B.35° C.36° D.40°
∠4=∠2,再根据两直线平行,同旁内角互补求出∠CAB+∠ABD=180°,然后计算即可得解.
【解答】解:如图,过点A作l1的平行线AC,过点B作l2的平行线BD,
则∠3=∠1,∠4=∠2,
∵l1∥l2,
∴AC∥BD,
∴∠CAB+∠ABD=180°,
∴∠3+∠4=125°+85°﹣180°=30°,
∴∠1+∠2=30°.
故选:A.
8.(3分)式子2×2×2=23=8,此时3叫做以2为底8的对数,记为log28(即log28=3),一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n),如34=81,则4叫做以3为底81的对数,记为log381,则log381=4,同理log327=3,log33=1.由此可以得到下列式子:log381=log3(27×3)=log327+log33,且若logab=logac,则b=c,根据以上的信息及运关系,若log4(x+12)+log4x=2log4(x+2),则x=( )
A. B. C.7 D.
【解答】解:设a=log3(x+12),b=log3x,c=log3(x+2),
∴3a+b=x(x+12),32c=(x+2) (x+2)=(x+2)2,
∴a+b=log3x(x+12),,
∴,
∴x(x+12)=(x+2)2,
解得:.
故选:A.
二、填空题(共10小题,每题3分,共30分)
9.(3分)中国科研团队突破性研制全球最薄金属材料,材料的厚度仅为0.00000000058m,是头发丝的二十万分之一.将0.00000000058用科学记数法表示为 5.8×10﹣10 .
【解答】解:0.00000000058=5.8×10﹣10.
故答案为:5.8×10﹣10.
10.(3分)若3a=4,3b=2,则3a﹣b= 2 .
【解答】解:由条件可得3a﹣b=3a÷3b=4÷2=2;
故答案为:2.
11.(3分)已知某多边形的每个外角都等于36°,则这个多边形是 10 边形.
【解答】解:∵这个多边形的每个外角都等于36°,
∴这个多边形的边数是:360÷36=10,
故答案为:10.
12.(3分)已知(a+2)x|a|﹣1+y=5是二元一次方程,则a的值为 2 .
【解答】解:∵(a+2)x|a|﹣1+y=5是一个二元一次方程,
∴,
解得:a=2,
故答案为:2.
13.(3分)若x2﹣3(k+1)x+36是一个完全平方式,则k= 3或﹣5 .
【解答】解:由条件可得﹣3(k+1)x=±2×6x,
∴k+1=4或k+1=﹣4,
解得k=3或k=﹣5,
故答案为:3或﹣5.
14.(3分)若关于x,y的方程组的解满足3x﹣y≤1,则m的最大整数解为 0 .
【解答】解:,
①+②得:3x﹣y=3m+1,
∵关于x,y的方程组的解满足3x﹣y≤1,
∴3m+1≤1,
∴m≤0,
∴m的最大整数解为0,
故答案为:0.
15.(3分)用反证法证明“三角形中必有一个内角不大于60°”时,应假设 每一个内角都大于60° .
【解答】解:根据反证法可知:每一个内角都大于60°.
故答案为:每一个内角都大于60°.
16.(3分)如图,在4×4的正方形网格中有三个黑色正方形,请你在网格中再涂黑一个小正方形,使其与原有的黑色正方形构成一个中心对称图形,则可供选择的白色小正方形的个数为 3 .
【解答】解:如图所示:标有数字的3个位置都是中心对称图形.
故答案为:3.
17.(3分)设a1,a2,…,a2025是从﹣1,0,1这三个数中取值的一列数,若a1+a2+ +a2025=0,(a1+1)2+(a2+1)2+ +(a2025+1)2=3025,则a1,a2,…,a2025中值为﹣1或0的个数共有 1525 个.
【解答】解:设值为﹣1、0、1的个数分别为x、y、z,
根据题意:,
解得:x=500,y=1025,z=500.
∴值为﹣1或0的个数为x+y=1525.
故答案为:1525.
18.(3分)如图,在△AOB在和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,OD与OA重叠.若△AOB绕点O按每秒20°的速度沿逆时针方向旋转不停,在旋转过程中,若△AOB和△COD中第一次有一组边平行,则称之为第一次“边平行”,当旋转到 3643.5 秒时,第2025次边平行.
【解答】解:在△AOB和△COD中,∠AOB=∠COD=90°,∠A=40°,∠C=60°,
∴∠CDO=30°,∠ABO=50°如图,第1次边平行时,AB∥CO,
∴∠COB=180°﹣∠ABO=130°,
∴旋转了180°﹣130°=50°,旋转2.5(秒),
如图,第2次边平行时,CD∥BO,
∴∠BOD=∠D=30°,
∴旋转了90°﹣30°=60°,旋转3(秒),
如图,第3次边平行时,AC∥BD,设OB,CD交于点E,
∴∠DEB=∠ABO=50°,
∴∠BOD=∠BED﹣∠CDO=50°﹣30°=20°,
∴旋转了20°+90°=110°,旋转了5.5(秒),
如图,第4次边平行时,AB∥DO,
∴∠BOD=∠ABO=50°,
∴旋转了90°+50°=140°,旋转时间为7(秒),
如图,第5次边平行时,CD∥AO,
∴∠AOC=∠C=60°,
∴∠BOC=90°﹣∠AOC=30°,
∴∠BOD=90°﹣∠BOC=60°,
∴旋转了90°+60°=150°,旋转时间为7.5(秒),
如图,第6次边平行时,CO∥AB,
∵∠BOC=∠ABO=50°,
∴旋转了180°+50°=230°,旋转时间为11.5(秒),
如图,第7次边平行时,CD∥BO,
∴∠BOC=∠C=60°,
∴旋转了180°+60°=240°,
旋转时间为12(秒),
如图,第8次边平行时,CD∥AB,设直线OB交CD于点F,
∴∠DFO=180°﹣∠B=130°,
∴∠DOF=180°﹣130°﹣30°﹣20°,
∴旋转了180°+20°+90°=290°,
旋转时间为14.5(秒),
如图,第9次边平行时,OD∥AB,
∴∠AOD=∠BAO=40°,
∴旋转了360°﹣40°=320°,
旋转时间为16(秒),
如图,第10次边平行时,CD∥AO,
∠AOD=∠CDO=30°,
∴旋转了360°﹣30°=330°,
旋转时间为15.5 (秒),再旋转30°就回到初始位置,
∴△OAB旋转1周有10次边平行,旋转时间为18(秒),
∵2025÷10=202…5,
第2025次平行时,旋转了202周,再加7.5秒,
∴202×18+7.5=3643.5,
故答案为:3643.5.
三.解答题(共10小题,共96分)
19.(8分)计算:
(1);
(2)a a5﹣(2a3)2+a9÷a3.
【解答】解:(1)
=﹣1+3+1﹣8
=﹣5;
(2)a a5﹣(2a3)2+a9÷a3
=a6﹣4a6+a6
=﹣2a6.
20.(8分)(1)解方程组:;
(2)解不等式组:,并用数轴表示解集.
【解答】解:(1),
①×2+③得,7x=14,
解得x=2,
把x=2代入②得,2+4y=4,
解得y,
所以原方程组的解为;
(2),
解不等式①得,x<2,
解不等式②得,x≥﹣1,
把两个不等式的解集在数轴上表示为:
所以不等式组的解集为﹣1≤x<2.
21.(8分)先化简,再求值:(x﹣y)(x+y)﹣(y﹣4)2+x(y﹣x),其中.
【解答】解:原式=x2﹣y2﹣(y2﹣8y+16)+xy﹣x2
=x2﹣y2﹣y2+8y﹣16+xy﹣x2
=﹣2y2+8y﹣16+xy.
当时,原式=﹣8+16﹣16+1=﹣7.
22.(8分)如图,在边长为1的小正方形组成的网格中,将△ABC平移得到△A′B′C′,连接AA′,BB′.
(1)根据题意,补全图形;
(2)线段AA′与线段BB′之间的位置关系和数量关系是 AA'∥BB',AA'=BB' ;
(3)在BB′上画出一点P,使得∠PA′B′=∠ABC.
【解答】解:(1)如图所示.
(2)由题意得,线段AA′与线段BB′之间的位置关系和数量关系是AA'∥BB',AA'=BB'.
故答案为:AA'∥BB',AA'=BB'.
(3)如图,过点A'作B'C'的平行线,交BB'于点P,
∴∠PA′B′=∠A'B'C',
由平移得∠A'B'C'=∠ABC,
∴∠PA′B′=∠ABC,
则点P即为所求.
23.(10分)定义:任意两个数a,b,按规则c=(a+1)(b+1)运算得到一个新数c,称所得的新数c为a,b的“和积数”.
(1)若a=4,b=﹣2,求a,b的“和积数”c;
(2)若,求a,b的“和积数”c.
【解答】解:(1)c=(4+1)(﹣2+1)=﹣5;
(2)c=(a+1)(b+1)=ab+a+b+1,
由条件可知(a+b)2=a2+b2+2ab=8+1=9,
∴a+b=3或a+b=﹣3,
当a+b=3时,,
当a+b=﹣3时,,
综上所述:c得值为或.
24.(10分)如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF=70°,∠D=30°,求∠AEM的度数.
【解答】解:(1)∠AED+∠D=180°;
∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠D=∠BED,
∴∠AED+∠D=180°;
(2)∵∠DHG=∠EHF=70°,∠D=30°,
∴∠HGD=80°,
∴∠CGF=180°﹣80°=100°,
∵CE∥GF,
∴∠C=180°﹣∠CGF=180°﹣100°=80°,
∵AB∥CD,
∴∠AEC=∠C=80°,
∴∠AEM=180°﹣∠AEC=180°﹣80°=100°.
25.(10分)如图,在△ABC中,∠C=90°,∠A=30°,请用无刻度直尺和圆规作图.(标注字母,保留作图痕迹,不要求写作法)
(1)图①,在边AC上找一点D,使得∠BDC=60°;
(2)图②,E是AB上一点,在边AC上作点F,使∠EFC=2∠A.
【解答】解:(1)如图①,作线段AB的垂直平分线,交AC于点D,
则AD=BD,
∴∠ABD=∠A=30°,
∴∠BDC=∠ABD+∠A=60°,
则点D即为所求.
(2)如图②,作线段AE的垂直平分线,交AC于点F,
则AF=EF,
∴∠AEF=∠A,
∴∠EFC=∠AEF+∠A=2∠A,
则点F即为所求.
26.(10分)某奶茶店推出A、B两款新品奶茶,已知购买5杯A奶茶和4杯B奶茶共花费130元,购买3杯A奶茶和2杯B奶茶共花费72元.
(1)求A、B两款奶茶的单价各为多少元?
(2)某班参加社会实践活动的有56位学生和4名教师,现该班决定团购下午茶,恰逢A、B两款新品奶茶搞促销活动,其中A奶茶在原来单价的基础上优惠5元,B奶茶在原来单价的基础上打八折,在班级现有经费648元的情况下,若B奶茶的数量不少于34杯,且所有参加活动的师生均有下午茶享用,则共有哪几种购买方案?哪种方案花费最少?最少费用多少元?
【解答】解:(1)设A款奶茶的单价为x元,B款奶茶的单价为y元,
根据题意得:,
解得:,
答:A款奶茶的单价为14元,B款奶茶的单价为15元;
(2)设购买A宽奶茶m杯,则购买B宽奶茶(60﹣m)杯,
根据题意得:,
解得:24≤m≤26,
∵m为正整数,
∴m可以为24,25,26,
∴共有3种购买方案:
①购买A奶茶24杯,购买B奶茶36杯,花费(14﹣5)×24+15×0.8×36=648(元);
②购买A奶茶25杯,购买B奶茶35杯,花费(14﹣5)×25+15×0.8×35=645(元);
③购买A奶茶26杯,购买B奶茶34杯,花费(14﹣5)×26+15×0.8×34=642(元);
∵648>645>642,
∴购买A奶茶26杯,购买B奶茶34杯最少,最少费用为642元,
答:共有3种购买方案,①购买A奶茶24杯,购买B奶茶36杯;②购买A奶茶25杯,购买B奶茶35杯;③购买A奶茶26杯,购买B奶茶34杯;购买A奶茶26杯,购买B奶茶34杯最少,最少费用为642元.
27.(12分)若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”.
例如,方程x﹣1=3的解为x=4,而不等式组的解集为2<x<5,不难发现x=4在2<x<5的范围内,所以方程x﹣1=3是不等式组的“关联方程”.
(1)请判断,方程3(x+1)﹣x=9 是 (“是”或“不是”)不等式组的“关联方程”;
(2)若关于x的方程2x﹣k=6是不等式组的“关联方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“关联方程”.且此时不等式组有4个整数解,试求m的取值范围.
【解答】解:(1)由题意,∵3(x+1)﹣x=9,
∴x=3.
又∵不等式组为,
∴1<x≤5.
∴方程3(x+1)﹣x=9是不等式组的“关联方程”.
故答案为:是.
(2)由题意,∵2x﹣k=6,
∴x.
又∵不等式组为,
∴﹣1≤x≤7.
∴﹣17.
∴﹣8≤k≤8.
(3)由题意,∵,
∴x=6m﹣7.
又由不等式组,
∴解不等式①得:x>0,解不等式②得:x≤3m+1,
∴原不等式组的解集为:0<x≤3m+1,
∵不等式组有4个整数解,
∴整数的值为1,2,3,4,
∴4≤3m+1<5.
∴.
∵关于x的方程是关于x的不等式组的“关联方程”,
∴.
∴.
∴m的取值范围是.
28.(12分)【问题探究】
(1)已知:如图1,在△ABC中,∠A=60°,BP,CP分别平分∠ABC和∠ACB,∠BPC的度数是 120° ;
(2)已知:如图2,∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,则∠A= 30° ;
【拓展与应用】
(3)如图3,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β,求∠F的度数;(用含α,β的式子表示)
(4)如图4,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=130°,则∠BIC= 122.5° .
【解答】解:(1)在△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵BP,CP分别平分∠ABC和∠ACB,
∴,,
∴,
∴∠BPC=180°﹣(∠PBC+∠PCB)=120°;
故答案为:120°;
(2)∵∠DBC与∠ECB分别是△ABC的两个外角,且∠DBC+∠ECB=210°,
∴∠ABC+∠ACB=180°+180°﹣(∠DBC+∠ECB)=360°﹣210°=150°,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣150°=30°;
故答案为:30°;
(3)延长BA,CD交于点Q,
∵∠BAD=α,∠ADC=β,同(2)可得∠Q=α+β﹣180°,
∵∠F为四边形ABCD的∠ABC 的平分线及外角∠DCE的平分线所在的直线构成的锐角,
∴,,
∵∠DCE=∠QBC+∠Q,∠FCE=∠FBC+∠F,
∴∠Q=∠DCE﹣∠QBC,2∠F=2∠FCE﹣2∠FBC=∠DCE﹣∠QBC,
∴∠Q=2∠F,
∴,
(4)∵∠1+∠2=130°,结合折叠,
∴∠ADI+AEI=180°+180°﹣(∠1+∠2)=230°,∠A=∠DIE,
∴65°,
∵BI平分∠ABC,CI平分∠ACB,
由(1)得:90°+32.5°=122.5°.
故答案为:122.5°.
同课章节目录
