2024-2025学年江苏省镇江市丹徒区八年级(下)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年江苏省镇江市丹徒区八年级(下)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 15:17:23 | ||
图片预览




文档简介
2024-2025学年江苏省镇江市丹徒区八年级(下)期末数学试卷
一、选择题(本大题共10小题,每小题3分,共计30分.每题只有一个正确选项.)
1.(3分)一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下列事件中,发生可能性最大的是( )
A.摸出的是白球 B.摸出的是黑球
C.摸出的是红球 D.摸出的是绿球
2.(3分)若代数式有意义,则a的取值范围应是( )
A.a>0 B.a=0 C.a<0 D.a≥0
3.(3分)下列调查中,最适合抽样调查的是( )
A.调查某校八年级一班学生的课余体育运动情况
B.调查你班每位同学所穿鞋子的尺码
C.调查某品牌灯泡的使用寿命
D.调查我校足球队员的身高情况
4.(3分)已知反比例函数的图象经过点(﹣2,3),则这个反比例函数的解析式为( )
A. B. C. D.
5.(3分)下列计算错误的是( )
A. B. C. D.
6.(3分)如图,四边形ABCD是平行四边形,对角线AC、BD交于点O,则下列结论正确的是( )
A.当AB⊥BC时,它是矩形
B.当∠ABC=90°时,它是正方形
C.当AC⊥BD时,它是矩形
D.当AC=BD时,它是菱形
7.(3分)若点A(2,y1)、B(3,y2)都在反比例函数(k>0)的图象上,则y1,y2的大小关系为( )
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
8.(3分)如图,正比例函数y1=2x的图象与反比例函数的图象相交于A、B两点,点A的横坐标为﹣1,当y1<y2时,x的取值范围为( )
A.x<﹣1或x>1 B.﹣1<x<0或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或0<x<1
9.(3分)如图,在菱形ABCD中,AB=8,E是BC的中点,连接AE,将AB沿着AE翻折,点B与点C正好重合,则AE等于( )
A.2 B. C. D.4
10.(3分)如图,菱形ABCD中,E,F分别是边CD,BC上的动点(E,F不与菱形的顶点重合),连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠BAD=150°,GH的最小值是,则菱形的边长是( )
A. B. C.6 D.3
二、填空题(本大题共6小题,每小题3分,共计18分.不需要写出解答过程)
11.(3分)从甲、乙、丙三名学生中随机选出一名学生参加问卷调查,则选出乙的可能性是 .
12.(3分)若分式的值为0,则x的值为 .
13.(3分)若与最简二次根式是同类二次根式,则m= .
14.(3分)若反比例函数的图象在每一象限内,y随x的增大而增大,则k的取值范围是 .
15.(3分)关于x的分式方程无解,则m= .
16.(3分)如图,点A在反比例函数的图象上,作AB⊥x轴,垂足为B,线段AB交反比例函数的图象于点C,点D是y轴正半轴上一点,连接AD、BD、CD,如果n﹣m=10,则△ACD的面积为 .
三、解答题(本大题共8小题,共计72分,请在答题卡指定区域内作答,解答时应写出必要的文字说明或演算步骤)
17.(12分)(1)解方程:;
(2)化简:;
(3)计算:.
18.(7分)如图,在正方形ABCD中,E、F是对角线AC上的两点,AE=CF.
求证:四边形BEDF是菱形.
19.(7分)数学文化有利于激发学生数学学习兴趣.某校为了解学生数学文化知识掌握的情况,从该校七年级学生中随机抽取20名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示,共分三组:A.90≤x≤100,B.80≤x<90,C.70≤x<80).
七年级20名学生的竞赛成绩如下:
85,87,76,87,87,80,82,84,74,87,92,78,78,93,95,96,81,82,97,98.
根据以上信息,解答下列问题:
(1)填写表格:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 10
频率 0.5 0.2
(2)根据以上数据,画出该校七年级学生竞赛成绩扇形统计图(如图),则扇形统计图中A组对应的圆心角的度数是 °;
(3)该校七年级学生有180人,估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有多少人?
20.(8分)在正方形网格中,每个小正方形边长均为1个单位长度,线段AB的两个端点位置如图所示,请按要求画出图形.
(1)在图1中画一个平行四边形ABCD,使得点M是平行四边形ABCD的对称中心;
(2)在图2中画一个平行四边形ABEF,使得平行四边形ABEF的周长是整数且邻边不垂直.
21.(8分)一辆货车从北京开往乌鲁木齐,路线总长是3780km,为了实施西部大开发,京乌线决定全线提速,提速后的平均速度是原来的倍,提速后比提速前可提前7h到达.
(1)提速前的平均速度是多少?
(2)如果全程运行时间控制40h内,那么提速后的平均速度至少应为多少?
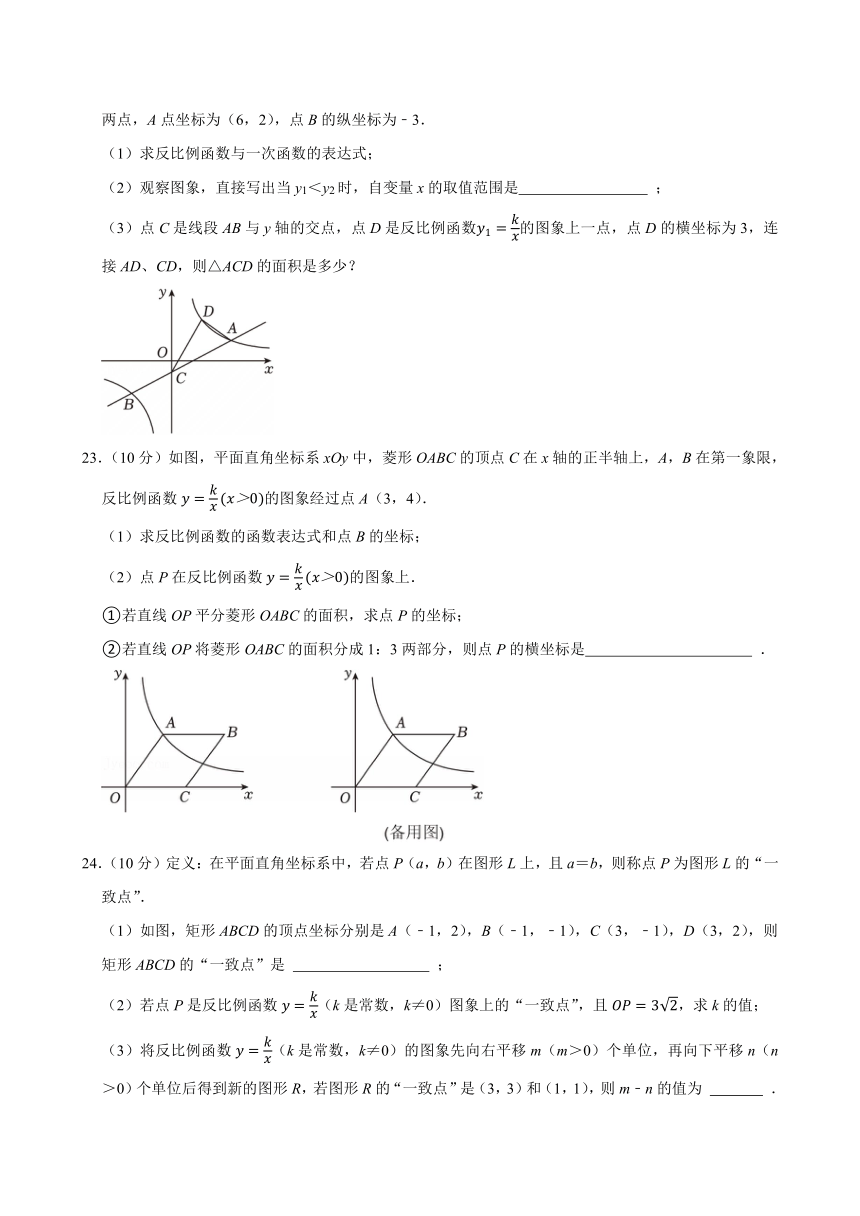
22.(10分)如图,反比例函数(k为常数,k≠0)的图象与一次函数的图象交于A、B两点,A点坐标为(6,2),点B的纵坐标为﹣3.
(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当y1<y2时,自变量x的取值范围是 ;
(3)点C是线段AB与y轴的交点,点D是反比例函数的图象上一点,点D的横坐标为3,连接AD、CD,则△ACD的面积是多少?
23.(10分)如图,平面直角坐标系xOy中,菱形OABC的顶点C在x轴的正半轴上,A,B在第一象限,反比例函数的图象经过点A(3,4).
(1)求反比例函数的函数表达式和点B的坐标;
(2)点P在反比例函数的图象上.
①若直线OP平分菱形OABC的面积,求点P的坐标;
②若直线OP将菱形OABC的面积分成1:3两部分,则点P的横坐标是 .
24.(10分)定义:在平面直角坐标系中,若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”.
(1)如图,矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),则矩形ABCD的“一致点”是 ;
(2)若点P是反比例函数(k是常数,k≠0)图象上的“一致点”,且,求k的值;
(3)将反比例函数(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,若图形R的“一致点”是(3,3)和(1,1),则m﹣n的值为 .
2024-2025学年江苏省镇江市丹徒区八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C D D A C C B C
一、选择题(本大题共10小题,每小题3分,共计30分.每题只有一个正确选项.)
1.(3分)一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下列事件中,发生可能性最大的是( )
A.摸出的是白球 B.摸出的是黑球
C.摸出的是红球 D.摸出的是绿球
【解答】解:因为白球最多,
所以被摸到的可能性最大.
故选:A.
2.(3分)若代数式有意义,则a的取值范围应是( )
A.a>0 B.a=0 C.a<0 D.a≥0
【解答】解:代数式有意义,则a是非负数,
即a≥0.
故选:D.
3.(3分)下列调查中,最适合抽样调查的是( )
A.调查某校八年级一班学生的课余体育运动情况
B.调查你班每位同学所穿鞋子的尺码
C.调查某品牌灯泡的使用寿命
D.调查我校足球队员的身高情况
【解答】解:调查某校八年级一班学生的课余体育运动情况适合全面调查,则A不符合题意,
调查你班每位同学所穿鞋子的尺码适合全面调查,则B不符合题意,
调查某品牌灯泡的使用寿命适合抽样调查,则C符合题意,
调查我校足球队员的身高情况适合全面调查,则D不符合题意,
故选:C.
4.(3分)已知反比例函数的图象经过点(﹣2,3),则这个反比例函数的解析式为( )
A. B. C. D.
【解答】解:设反比例函数的解析式y,
把点(﹣2,3)代入得3,解得k=﹣6,
则反比例函数的解析式是y,
故选:D.
5.(3分)下列计算错误的是( )
A. B. C. D.
【解答】解:A.,故选项A正确;
B.,故选项B正确;
C.,故选项C正确;
D.,故选项D错误.
故选:D.
6.(3分)如图,四边形ABCD是平行四边形,对角线AC、BD交于点O,则下列结论正确的是( )
A.当AB⊥BC时,它是矩形
B.当∠ABC=90°时,它是正方形
C.当AC⊥BD时,它是矩形
D.当AC=BD时,它是菱形
【解答】解:A、∵四边形ABCD是平行四边形,当AB⊥BC,
∴平行四边形ABCD是矩形,故符合题意;
B、∵四边形ABCD是平行四边形,∠ABC=90°,
∴平行四边形ABCD是矩形,故不符合题意;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故不符合题意;
故选:A.
7.(3分)若点A(2,y1)、B(3,y2)都在反比例函数(k>0)的图象上,则y1,y2的大小关系为( )
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
【解答】解:k>0,
∴图象的分支在第一、三象限,
在同一象限内,y随x的增大而减小,2<3,
∴y1>y2.
故选:C.
8.(3分)如图,正比例函数y1=2x的图象与反比例函数的图象相交于A、B两点,点A的横坐标为﹣1,当y1<y2时,x的取值范围为( )
A.x<﹣1或x>1 B.﹣1<x<0或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或0<x<1
【解答】解:∵正比例函数y1=2x的图象与反比例函数的图象关于原点对称,
∴两函数的交点A,B关于原点对称,
∵点A的横坐标为﹣1,
∴点B的横坐标为1,
当y1<y2时,反比例函数的图象在正比例函数图象的上方,即第一象限内点B的左侧和第三象限内点A的左侧,
∴当y1<y2时,x的取值范围为x<﹣1或0<x<1,
故选:C.
9.(3分)如图,在菱形ABCD中,AB=8,E是BC的中点,连接AE,将AB沿着AE翻折,点B与点C正好重合,则AE等于( )
A.2 B. C. D.4
【解答】解:∵四边形ABCD是菱形,AB=8,E是BC的中点,
∴AB=CB=8,
∴BE=CEBC=4,
∵将AB沿着AE翻折,点B与点C正好重合,
∴∠AEB=∠AEC180°=90°,
∴AE4,
故选:B.
10.(3分)如图,菱形ABCD中,E,F分别是边CD,BC上的动点(E,F不与菱形的顶点重合),连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠BAD=150°,GH的最小值是,则菱形的边长是( )
A. B. C.6 D.3
【解答】解:连接AF,
∵G,H分别为AE,EF的中点,
∴AF=2GH,
∴当AF⊥BC时,GH有最小值,
∴此时AF=2GH=3,
∵四边形ABCD是菱形,∠BAD=150°,
∴∠B=30°,
∴AB=2AF=6,
故选:C.
二、填空题(本大题共6小题,每小题3分,共计18分.不需要写出解答过程)
11.(3分)从甲、乙、丙三名学生中随机选出一名学生参加问卷调查,则选出乙的可能性是 .
【解答】解:从甲、乙、丙三名学生参加问卷调查共有3种等可能结果,其中选出乙的有1种结果,
所以选出女生的概率为,
故答案为:.
12.(3分)若分式的值为0,则x的值为 .
【解答】解:分式的值为0,
则2x﹣1=0,
解得:x.
故答案为:.
13.(3分)若与最简二次根式是同类二次根式,则m= 1 .
【解答】解:∵与最简二次根式是同类二次根式,
∴2m+1=3,
移项、合并同类项,得2m=2,
解得:m=1.
故答案为:1.
14.(3分)若反比例函数的图象在每一象限内,y随x的增大而增大,则k的取值范围是 k<3 .
【解答】解:∵反比例函数y的图象,在每个象限内y随x的增大而增大,
∴k﹣3<0,解得k<3.
故答案为:k<3.
15.(3分)关于x的分式方程无解,则m= ﹣1 .
【解答】解:将分式方程的两边都乘以x﹣1,得
m﹣x=﹣2,
解得x=m+2,
由于分式方程无解,即分式方程有增根x=1,
当x=1时,m=1﹣2=﹣1,
故答案为:﹣1.
16.(3分)如图,点A在反比例函数的图象上,作AB⊥x轴,垂足为B,线段AB交反比例函数的图象于点C,点D是y轴正半轴上一点,连接AD、BD、CD,如果n﹣m=10,则△ACD的面积为 5 .
【解答】解:如图,连接AO、CO,
∵AB∥y轴,点A在反比例函数的图象上,线段AB交反比例函数的图象于点C,
∴S△ABD=S△ABO,S△CBD=S△CBO,
∵n﹣m=10,
∴S△ACD=S△ABD﹣S△CBD|n﹣m|5,
故答案为:5.
三、解答题(本大题共8小题,共计72分,请在答题卡指定区域内作答,解答时应写出必要的文字说明或演算步骤)
17.(12分)(1)解方程:;
(2)化简:;
(3)计算:.
【解答】解:(1)去分母,得1+2(x﹣2)=﹣(3﹣x),
去括号,得1+2x﹣4=﹣3+x,
移项,得2x﹣x=﹣3﹣1+4,
合并,得x=0,
检验:当x=0时,x﹣2≠0,则x=0为原方程的解,
所以原方程的解为x=0;
(2)原式
;
(3)原式=8﹣3﹣2
=3.
18.(7分)如图,在正方形ABCD中,E、F是对角线AC上的两点,AE=CF.
求证:四边形BEDF是菱形.
【解答】证明:连接BD交AC于O,
∵四边形ABCD是正方形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴平行四边形BEDF是菱形.
19.(7分)数学文化有利于激发学生数学学习兴趣.某校为了解学生数学文化知识掌握的情况,从该校七年级学生中随机抽取20名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示,共分三组:A.90≤x≤100,B.80≤x<90,C.70≤x<80).
七年级20名学生的竞赛成绩如下:
85,87,76,87,87,80,82,84,74,87,92,78,78,93,95,96,81,82,97,98.
根据以上信息,解答下列问题:
(1)填写表格:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 6 10 4
频率 0.3 0.5 0.2
(2)根据以上数据,画出该校七年级学生竞赛成绩扇形统计图(如图),则扇形统计图中A组对应的圆心角的度数是 108 °;
(3)该校七年级学生有180人,估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有多少人?
【解答】解:(1)补全表格如下:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 6 10 4
频率 0.3 0.5 0.2
(2)扇形统计图中A组对应的圆心角的度数是360°×0.3=108°,
故答案为:108;
(3)180×(0.3+0.5)=144(人),
答:估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有144人.
20.(8分)在正方形网格中,每个小正方形边长均为1个单位长度,线段AB的两个端点位置如图所示,请按要求画出图形.
(1)在图1中画一个平行四边形ABCD,使得点M是平行四边形ABCD的对称中心;
(2)在图2中画一个平行四边形ABEF,使得平行四边形ABEF的周长是整数且邻边不垂直.
【解答】解:(1)如图1,平行四边形ABCD即为所求.
(2)如图2,平行四边形ABEF即为所求.
21.(8分)一辆货车从北京开往乌鲁木齐,路线总长是3780km,为了实施西部大开发,京乌线决定全线提速,提速后的平均速度是原来的倍,提速后比提速前可提前7h到达.
(1)提速前的平均速度是多少?
(2)如果全程运行时间控制40h内,那么提速后的平均速度至少应为多少?
【解答】解:(1)设提速前的平均速度是x km/h,则提速前的平均速度是km/h,
由题意得:7,
解得:x=60,
经检验,x=60是原方程的解,且符合题意,
答:提速前的平均速度是60km/h;
(2)设提速后的平均速度应为y km/h,
由题意得:40y≥3780,
解得:y≥94.5,
答:提速后的平均速度至少应为94.5km/h.
22.(10分)如图,反比例函数(k为常数,k≠0)的图象与一次函数的图象交于A、B两点,A点坐标为(6,2),点B的纵坐标为﹣3.
(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当y1<y2时,自变量x的取值范围是 x>6或﹣4<x<0 ;
(3)点C是线段AB与y轴的交点,点D是反比例函数的图象上一点,点D的横坐标为3,连接AD、CD,则△ACD的面积是多少?
【解答】解:(1)一次函数图象上A点坐标为(6,2),点B的纵坐标为﹣3.
∴2b,解得b=﹣1,
∴一次函数解析式为y2,B(﹣4,﹣3),
反比例函数解析式为y;
(2)观察图象,当y1<y2时,自变量x的取值范围是x>6或﹣4<x<0,
故答案为:x>6或﹣4<x<0;
(3)过点D作x轴的垂线交直线AB于点E,
∵点C是线段AB与y轴的交点,点D的横坐标为3,
∴C(0,﹣1),D(3,4),
在直线y=x﹣1中,当x=3时,y=2,
∴E(3,2),
∴DE=2,
S△ACD6.
23.(10分)如图,平面直角坐标系xOy中,菱形OABC的顶点C在x轴的正半轴上,A,B在第一象限,反比例函数的图象经过点A(3,4).
(1)求反比例函数的函数表达式和点B的坐标;
(2)点P在反比例函数的图象上.
①若直线OP平分菱形OABC的面积,求点P的坐标;
②若直线OP将菱形OABC的面积分成1:3两部分,则点P的横坐标是 或 .
【解答】解:(1)把A(3,4)代入y得:4,
解得k=12,
∴反比例函数的函数表达式为y;
∵A(3,4),
∴OA5,
∵四边形OABC是菱形,
∴AB=OA=5=OC,AB∥x轴,
∴B(8,4);
(2)①∵B(8,4),
∴菱形OABC的对称中心为OB的中点(4,2),
∵直线OP平分菱形OABC的面积,
∴直线OP经过点(4,2),此时直线OP的解析式为yx,
联立,
解得或,
∴P(2,);
②∵A(3,4),OC=5,
∴S菱形OABC=5×4=20,
当直线OP交边AB于H,S△OAH:S四边形HOCB=1:3时,如图:
∴S△OAHS菱形OABC=5,
∴AH×4=5,
∴AH,
∴H(,4),
∴直线OH解析式为yx,
联立可得x,
解得x或x(舍去),
∴P的横坐标为;
当直线OP交边BC于H',S△OCH':S四边形H'OAB=1:3时,如图:
∴S△OCH'S菱形OABC=5,
∴yH'×5=5,
∴yH'=2,
由B(8,4),C(5,0)得直线BC解析式为yx,
令y=2得x,
∴H'(,2),
∴直线OH'解析式为yx,
联立得x,
解得x或x(舍去);
∴P的横坐标为;
综上所述,P的横坐标为或.
24.(10分)定义:在平面直角坐标系中,若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”.
(1)如图,矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),则矩形ABCD的“一致点”是 (1,1)和(2,2) ;
(2)若点P是反比例函数(k是常数,k≠0)图象上的“一致点”,且,求k的值;
(3)将反比例函数(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,若图形R的“一致点”是(3,3)和(1,1),则m﹣n的值为 4 .
【解答】解:(1)∵若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”,
∴b=a,
∴点P(a,a),
∴点P在直线y=x上,
如图,
∵矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),
∴当x=﹣1时,y=x=1,
∴点(1,1)是矩形ABCD的“一致点”;
当y=2时,得:x=2,
∴点(2,2)是矩形ABCD的“一致点”;
综上所述,矩形ABCD的“一致点”的是(1,1)和(2,2),
故答案为:(1,1)和(2,2);
(2)如图,设点P在第一象限,过点P作PQ⊥x轴,
∵点P为反比例函数y(k≠0)图象上的“一致点”,
∴点P在直线y=x上,
∴△POQ是等腰直角三角形,
∴PQ=OQ,PQ2+OQ2=OP2=(3)2,
∴PQ=OQ=3,
∴P(3,3),
∴将P(3,3)代入y(k≠0)得:3,
解得k=9,
故答案为:9;
(3)∵将反比例函数y(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,
∴新的图形R对应的表达式为yn,
∵图形R的“一致点”是(3,3)和(1,1),
∴,
由①得:k=(3﹣m)(3+n)③,
由②得:k=(1﹣m)(1+n)④,
∴(3﹣m)(3+n)=(1﹣m)(1+n),
∴m﹣n=4,
故答案为:4.
一、选择题(本大题共10小题,每小题3分,共计30分.每题只有一个正确选项.)
1.(3分)一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下列事件中,发生可能性最大的是( )
A.摸出的是白球 B.摸出的是黑球
C.摸出的是红球 D.摸出的是绿球
2.(3分)若代数式有意义,则a的取值范围应是( )
A.a>0 B.a=0 C.a<0 D.a≥0
3.(3分)下列调查中,最适合抽样调查的是( )
A.调查某校八年级一班学生的课余体育运动情况
B.调查你班每位同学所穿鞋子的尺码
C.调查某品牌灯泡的使用寿命
D.调查我校足球队员的身高情况
4.(3分)已知反比例函数的图象经过点(﹣2,3),则这个反比例函数的解析式为( )
A. B. C. D.
5.(3分)下列计算错误的是( )
A. B. C. D.
6.(3分)如图,四边形ABCD是平行四边形,对角线AC、BD交于点O,则下列结论正确的是( )
A.当AB⊥BC时,它是矩形
B.当∠ABC=90°时,它是正方形
C.当AC⊥BD时,它是矩形
D.当AC=BD时,它是菱形
7.(3分)若点A(2,y1)、B(3,y2)都在反比例函数(k>0)的图象上,则y1,y2的大小关系为( )
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
8.(3分)如图,正比例函数y1=2x的图象与反比例函数的图象相交于A、B两点,点A的横坐标为﹣1,当y1<y2时,x的取值范围为( )
A.x<﹣1或x>1 B.﹣1<x<0或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或0<x<1
9.(3分)如图,在菱形ABCD中,AB=8,E是BC的中点,连接AE,将AB沿着AE翻折,点B与点C正好重合,则AE等于( )
A.2 B. C. D.4
10.(3分)如图,菱形ABCD中,E,F分别是边CD,BC上的动点(E,F不与菱形的顶点重合),连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠BAD=150°,GH的最小值是,则菱形的边长是( )
A. B. C.6 D.3
二、填空题(本大题共6小题,每小题3分,共计18分.不需要写出解答过程)
11.(3分)从甲、乙、丙三名学生中随机选出一名学生参加问卷调查,则选出乙的可能性是 .
12.(3分)若分式的值为0,则x的值为 .
13.(3分)若与最简二次根式是同类二次根式,则m= .
14.(3分)若反比例函数的图象在每一象限内,y随x的增大而增大,则k的取值范围是 .
15.(3分)关于x的分式方程无解,则m= .
16.(3分)如图,点A在反比例函数的图象上,作AB⊥x轴,垂足为B,线段AB交反比例函数的图象于点C,点D是y轴正半轴上一点,连接AD、BD、CD,如果n﹣m=10,则△ACD的面积为 .
三、解答题(本大题共8小题,共计72分,请在答题卡指定区域内作答,解答时应写出必要的文字说明或演算步骤)
17.(12分)(1)解方程:;
(2)化简:;
(3)计算:.
18.(7分)如图,在正方形ABCD中,E、F是对角线AC上的两点,AE=CF.
求证:四边形BEDF是菱形.
19.(7分)数学文化有利于激发学生数学学习兴趣.某校为了解学生数学文化知识掌握的情况,从该校七年级学生中随机抽取20名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示,共分三组:A.90≤x≤100,B.80≤x<90,C.70≤x<80).
七年级20名学生的竞赛成绩如下:
85,87,76,87,87,80,82,84,74,87,92,78,78,93,95,96,81,82,97,98.
根据以上信息,解答下列问题:
(1)填写表格:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 10
频率 0.5 0.2
(2)根据以上数据,画出该校七年级学生竞赛成绩扇形统计图(如图),则扇形统计图中A组对应的圆心角的度数是 °;
(3)该校七年级学生有180人,估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有多少人?
20.(8分)在正方形网格中,每个小正方形边长均为1个单位长度,线段AB的两个端点位置如图所示,请按要求画出图形.
(1)在图1中画一个平行四边形ABCD,使得点M是平行四边形ABCD的对称中心;
(2)在图2中画一个平行四边形ABEF,使得平行四边形ABEF的周长是整数且邻边不垂直.
21.(8分)一辆货车从北京开往乌鲁木齐,路线总长是3780km,为了实施西部大开发,京乌线决定全线提速,提速后的平均速度是原来的倍,提速后比提速前可提前7h到达.
(1)提速前的平均速度是多少?
(2)如果全程运行时间控制40h内,那么提速后的平均速度至少应为多少?
22.(10分)如图,反比例函数(k为常数,k≠0)的图象与一次函数的图象交于A、B两点,A点坐标为(6,2),点B的纵坐标为﹣3.
(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当y1<y2时,自变量x的取值范围是 ;
(3)点C是线段AB与y轴的交点,点D是反比例函数的图象上一点,点D的横坐标为3,连接AD、CD,则△ACD的面积是多少?
23.(10分)如图,平面直角坐标系xOy中,菱形OABC的顶点C在x轴的正半轴上,A,B在第一象限,反比例函数的图象经过点A(3,4).
(1)求反比例函数的函数表达式和点B的坐标;
(2)点P在反比例函数的图象上.
①若直线OP平分菱形OABC的面积,求点P的坐标;
②若直线OP将菱形OABC的面积分成1:3两部分,则点P的横坐标是 .
24.(10分)定义:在平面直角坐标系中,若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”.
(1)如图,矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),则矩形ABCD的“一致点”是 ;
(2)若点P是反比例函数(k是常数,k≠0)图象上的“一致点”,且,求k的值;
(3)将反比例函数(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,若图形R的“一致点”是(3,3)和(1,1),则m﹣n的值为 .
2024-2025学年江苏省镇江市丹徒区八年级(下)期末数学试卷
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 A D C D D A C C B C
一、选择题(本大题共10小题,每小题3分,共计30分.每题只有一个正确选项.)
1.(3分)一个布袋里装有2个红球,3个黑球,4个白球,它们除颜色外都相同,从中任意摸出1个球,则下列事件中,发生可能性最大的是( )
A.摸出的是白球 B.摸出的是黑球
C.摸出的是红球 D.摸出的是绿球
【解答】解:因为白球最多,
所以被摸到的可能性最大.
故选:A.
2.(3分)若代数式有意义,则a的取值范围应是( )
A.a>0 B.a=0 C.a<0 D.a≥0
【解答】解:代数式有意义,则a是非负数,
即a≥0.
故选:D.
3.(3分)下列调查中,最适合抽样调查的是( )
A.调查某校八年级一班学生的课余体育运动情况
B.调查你班每位同学所穿鞋子的尺码
C.调查某品牌灯泡的使用寿命
D.调查我校足球队员的身高情况
【解答】解:调查某校八年级一班学生的课余体育运动情况适合全面调查,则A不符合题意,
调查你班每位同学所穿鞋子的尺码适合全面调查,则B不符合题意,
调查某品牌灯泡的使用寿命适合抽样调查,则C符合题意,
调查我校足球队员的身高情况适合全面调查,则D不符合题意,
故选:C.
4.(3分)已知反比例函数的图象经过点(﹣2,3),则这个反比例函数的解析式为( )
A. B. C. D.
【解答】解:设反比例函数的解析式y,
把点(﹣2,3)代入得3,解得k=﹣6,
则反比例函数的解析式是y,
故选:D.
5.(3分)下列计算错误的是( )
A. B. C. D.
【解答】解:A.,故选项A正确;
B.,故选项B正确;
C.,故选项C正确;
D.,故选项D错误.
故选:D.
6.(3分)如图,四边形ABCD是平行四边形,对角线AC、BD交于点O,则下列结论正确的是( )
A.当AB⊥BC时,它是矩形
B.当∠ABC=90°时,它是正方形
C.当AC⊥BD时,它是矩形
D.当AC=BD时,它是菱形
【解答】解:A、∵四边形ABCD是平行四边形,当AB⊥BC,
∴平行四边形ABCD是矩形,故符合题意;
B、∵四边形ABCD是平行四边形,∠ABC=90°,
∴平行四边形ABCD是矩形,故不符合题意;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故不符合题意;
故选:A.
7.(3分)若点A(2,y1)、B(3,y2)都在反比例函数(k>0)的图象上,则y1,y2的大小关系为( )
A.y1<y2 B.y1≤y2 C.y1>y2 D.y1≥y2
【解答】解:k>0,
∴图象的分支在第一、三象限,
在同一象限内,y随x的增大而减小,2<3,
∴y1>y2.
故选:C.
8.(3分)如图,正比例函数y1=2x的图象与反比例函数的图象相交于A、B两点,点A的横坐标为﹣1,当y1<y2时,x的取值范围为( )
A.x<﹣1或x>1 B.﹣1<x<0或x>1
C.x<﹣1或0<x<1 D.﹣1<x<0或0<x<1
【解答】解:∵正比例函数y1=2x的图象与反比例函数的图象关于原点对称,
∴两函数的交点A,B关于原点对称,
∵点A的横坐标为﹣1,
∴点B的横坐标为1,
当y1<y2时,反比例函数的图象在正比例函数图象的上方,即第一象限内点B的左侧和第三象限内点A的左侧,
∴当y1<y2时,x的取值范围为x<﹣1或0<x<1,
故选:C.
9.(3分)如图,在菱形ABCD中,AB=8,E是BC的中点,连接AE,将AB沿着AE翻折,点B与点C正好重合,则AE等于( )
A.2 B. C. D.4
【解答】解:∵四边形ABCD是菱形,AB=8,E是BC的中点,
∴AB=CB=8,
∴BE=CEBC=4,
∵将AB沿着AE翻折,点B与点C正好重合,
∴∠AEB=∠AEC180°=90°,
∴AE4,
故选:B.
10.(3分)如图,菱形ABCD中,E,F分别是边CD,BC上的动点(E,F不与菱形的顶点重合),连接AE,EF,G,H分别为AE,EF的中点,连接GH.若∠BAD=150°,GH的最小值是,则菱形的边长是( )
A. B. C.6 D.3
【解答】解:连接AF,
∵G,H分别为AE,EF的中点,
∴AF=2GH,
∴当AF⊥BC时,GH有最小值,
∴此时AF=2GH=3,
∵四边形ABCD是菱形,∠BAD=150°,
∴∠B=30°,
∴AB=2AF=6,
故选:C.
二、填空题(本大题共6小题,每小题3分,共计18分.不需要写出解答过程)
11.(3分)从甲、乙、丙三名学生中随机选出一名学生参加问卷调查,则选出乙的可能性是 .
【解答】解:从甲、乙、丙三名学生参加问卷调查共有3种等可能结果,其中选出乙的有1种结果,
所以选出女生的概率为,
故答案为:.
12.(3分)若分式的值为0,则x的值为 .
【解答】解:分式的值为0,
则2x﹣1=0,
解得:x.
故答案为:.
13.(3分)若与最简二次根式是同类二次根式,则m= 1 .
【解答】解:∵与最简二次根式是同类二次根式,
∴2m+1=3,
移项、合并同类项,得2m=2,
解得:m=1.
故答案为:1.
14.(3分)若反比例函数的图象在每一象限内,y随x的增大而增大,则k的取值范围是 k<3 .
【解答】解:∵反比例函数y的图象,在每个象限内y随x的增大而增大,
∴k﹣3<0,解得k<3.
故答案为:k<3.
15.(3分)关于x的分式方程无解,则m= ﹣1 .
【解答】解:将分式方程的两边都乘以x﹣1,得
m﹣x=﹣2,
解得x=m+2,
由于分式方程无解,即分式方程有增根x=1,
当x=1时,m=1﹣2=﹣1,
故答案为:﹣1.
16.(3分)如图,点A在反比例函数的图象上,作AB⊥x轴,垂足为B,线段AB交反比例函数的图象于点C,点D是y轴正半轴上一点,连接AD、BD、CD,如果n﹣m=10,则△ACD的面积为 5 .
【解答】解:如图,连接AO、CO,
∵AB∥y轴,点A在反比例函数的图象上,线段AB交反比例函数的图象于点C,
∴S△ABD=S△ABO,S△CBD=S△CBO,
∵n﹣m=10,
∴S△ACD=S△ABD﹣S△CBD|n﹣m|5,
故答案为:5.
三、解答题(本大题共8小题,共计72分,请在答题卡指定区域内作答,解答时应写出必要的文字说明或演算步骤)
17.(12分)(1)解方程:;
(2)化简:;
(3)计算:.
【解答】解:(1)去分母,得1+2(x﹣2)=﹣(3﹣x),
去括号,得1+2x﹣4=﹣3+x,
移项,得2x﹣x=﹣3﹣1+4,
合并,得x=0,
检验:当x=0时,x﹣2≠0,则x=0为原方程的解,
所以原方程的解为x=0;
(2)原式
;
(3)原式=8﹣3﹣2
=3.
18.(7分)如图,在正方形ABCD中,E、F是对角线AC上的两点,AE=CF.
求证:四边形BEDF是菱形.
【解答】证明:连接BD交AC于O,
∵四边形ABCD是正方形,
∴OB=OD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴平行四边形BEDF是菱形.
19.(7分)数学文化有利于激发学生数学学习兴趣.某校为了解学生数学文化知识掌握的情况,从该校七年级学生中随机抽取20名学生参加了数学文化知识竞赛,并对数据(百分制)进行整理、描述和分析(成绩均不低于70分,用x表示,共分三组:A.90≤x≤100,B.80≤x<90,C.70≤x<80).
七年级20名学生的竞赛成绩如下:
85,87,76,87,87,80,82,84,74,87,92,78,78,93,95,96,81,82,97,98.
根据以上信息,解答下列问题:
(1)填写表格:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 6 10 4
频率 0.3 0.5 0.2
(2)根据以上数据,画出该校七年级学生竞赛成绩扇形统计图(如图),则扇形统计图中A组对应的圆心角的度数是 108 °;
(3)该校七年级学生有180人,估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有多少人?
【解答】解:(1)补全表格如下:
竞赛成绩(分) 90≤x≤100(A) 80≤x<90(B) 70≤x<80(C)
频数 6 10 4
频率 0.3 0.5 0.2
(2)扇形统计图中A组对应的圆心角的度数是360°×0.3=108°,
故答案为:108;
(3)180×(0.3+0.5)=144(人),
答:估计该校七年级学生中数学文化知识为“优秀”(x≥80)的总共有144人.
20.(8分)在正方形网格中,每个小正方形边长均为1个单位长度,线段AB的两个端点位置如图所示,请按要求画出图形.
(1)在图1中画一个平行四边形ABCD,使得点M是平行四边形ABCD的对称中心;
(2)在图2中画一个平行四边形ABEF,使得平行四边形ABEF的周长是整数且邻边不垂直.
【解答】解:(1)如图1,平行四边形ABCD即为所求.
(2)如图2,平行四边形ABEF即为所求.
21.(8分)一辆货车从北京开往乌鲁木齐,路线总长是3780km,为了实施西部大开发,京乌线决定全线提速,提速后的平均速度是原来的倍,提速后比提速前可提前7h到达.
(1)提速前的平均速度是多少?
(2)如果全程运行时间控制40h内,那么提速后的平均速度至少应为多少?
【解答】解:(1)设提速前的平均速度是x km/h,则提速前的平均速度是km/h,
由题意得:7,
解得:x=60,
经检验,x=60是原方程的解,且符合题意,
答:提速前的平均速度是60km/h;
(2)设提速后的平均速度应为y km/h,
由题意得:40y≥3780,
解得:y≥94.5,
答:提速后的平均速度至少应为94.5km/h.
22.(10分)如图,反比例函数(k为常数,k≠0)的图象与一次函数的图象交于A、B两点,A点坐标为(6,2),点B的纵坐标为﹣3.
(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当y1<y2时,自变量x的取值范围是 x>6或﹣4<x<0 ;
(3)点C是线段AB与y轴的交点,点D是反比例函数的图象上一点,点D的横坐标为3,连接AD、CD,则△ACD的面积是多少?
【解答】解:(1)一次函数图象上A点坐标为(6,2),点B的纵坐标为﹣3.
∴2b,解得b=﹣1,
∴一次函数解析式为y2,B(﹣4,﹣3),
反比例函数解析式为y;
(2)观察图象,当y1<y2时,自变量x的取值范围是x>6或﹣4<x<0,
故答案为:x>6或﹣4<x<0;
(3)过点D作x轴的垂线交直线AB于点E,
∵点C是线段AB与y轴的交点,点D的横坐标为3,
∴C(0,﹣1),D(3,4),
在直线y=x﹣1中,当x=3时,y=2,
∴E(3,2),
∴DE=2,
S△ACD6.
23.(10分)如图,平面直角坐标系xOy中,菱形OABC的顶点C在x轴的正半轴上,A,B在第一象限,反比例函数的图象经过点A(3,4).
(1)求反比例函数的函数表达式和点B的坐标;
(2)点P在反比例函数的图象上.
①若直线OP平分菱形OABC的面积,求点P的坐标;
②若直线OP将菱形OABC的面积分成1:3两部分,则点P的横坐标是 或 .
【解答】解:(1)把A(3,4)代入y得:4,
解得k=12,
∴反比例函数的函数表达式为y;
∵A(3,4),
∴OA5,
∵四边形OABC是菱形,
∴AB=OA=5=OC,AB∥x轴,
∴B(8,4);
(2)①∵B(8,4),
∴菱形OABC的对称中心为OB的中点(4,2),
∵直线OP平分菱形OABC的面积,
∴直线OP经过点(4,2),此时直线OP的解析式为yx,
联立,
解得或,
∴P(2,);
②∵A(3,4),OC=5,
∴S菱形OABC=5×4=20,
当直线OP交边AB于H,S△OAH:S四边形HOCB=1:3时,如图:
∴S△OAHS菱形OABC=5,
∴AH×4=5,
∴AH,
∴H(,4),
∴直线OH解析式为yx,
联立可得x,
解得x或x(舍去),
∴P的横坐标为;
当直线OP交边BC于H',S△OCH':S四边形H'OAB=1:3时,如图:
∴S△OCH'S菱形OABC=5,
∴yH'×5=5,
∴yH'=2,
由B(8,4),C(5,0)得直线BC解析式为yx,
令y=2得x,
∴H'(,2),
∴直线OH'解析式为yx,
联立得x,
解得x或x(舍去);
∴P的横坐标为;
综上所述,P的横坐标为或.
24.(10分)定义:在平面直角坐标系中,若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”.
(1)如图,矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),则矩形ABCD的“一致点”是 (1,1)和(2,2) ;
(2)若点P是反比例函数(k是常数,k≠0)图象上的“一致点”,且,求k的值;
(3)将反比例函数(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,若图形R的“一致点”是(3,3)和(1,1),则m﹣n的值为 4 .
【解答】解:(1)∵若点P(a,b)在图形L上,且a=b,则称点P为图形L的“一致点”,
∴b=a,
∴点P(a,a),
∴点P在直线y=x上,
如图,
∵矩形ABCD的顶点坐标分别是A(﹣1,2),B(﹣1,﹣1),C(3,﹣1),D(3,2),
∴当x=﹣1时,y=x=1,
∴点(1,1)是矩形ABCD的“一致点”;
当y=2时,得:x=2,
∴点(2,2)是矩形ABCD的“一致点”;
综上所述,矩形ABCD的“一致点”的是(1,1)和(2,2),
故答案为:(1,1)和(2,2);
(2)如图,设点P在第一象限,过点P作PQ⊥x轴,
∵点P为反比例函数y(k≠0)图象上的“一致点”,
∴点P在直线y=x上,
∴△POQ是等腰直角三角形,
∴PQ=OQ,PQ2+OQ2=OP2=(3)2,
∴PQ=OQ=3,
∴P(3,3),
∴将P(3,3)代入y(k≠0)得:3,
解得k=9,
故答案为:9;
(3)∵将反比例函数y(k是常数,k≠0)的图象先向右平移m(m>0)个单位,再向下平移n(n>0)个单位后得到新的图形R,
∴新的图形R对应的表达式为yn,
∵图形R的“一致点”是(3,3)和(1,1),
∴,
由①得:k=(3﹣m)(3+n)③,
由②得:k=(1﹣m)(1+n)④,
∴(3﹣m)(3+n)=(1﹣m)(1+n),
∴m﹣n=4,
故答案为:4.
同课章节目录
