21.3.3 几何图形问题 同步练习(含答案)
文档属性
| 名称 | 21.3.3 几何图形问题 同步练习(含答案) | 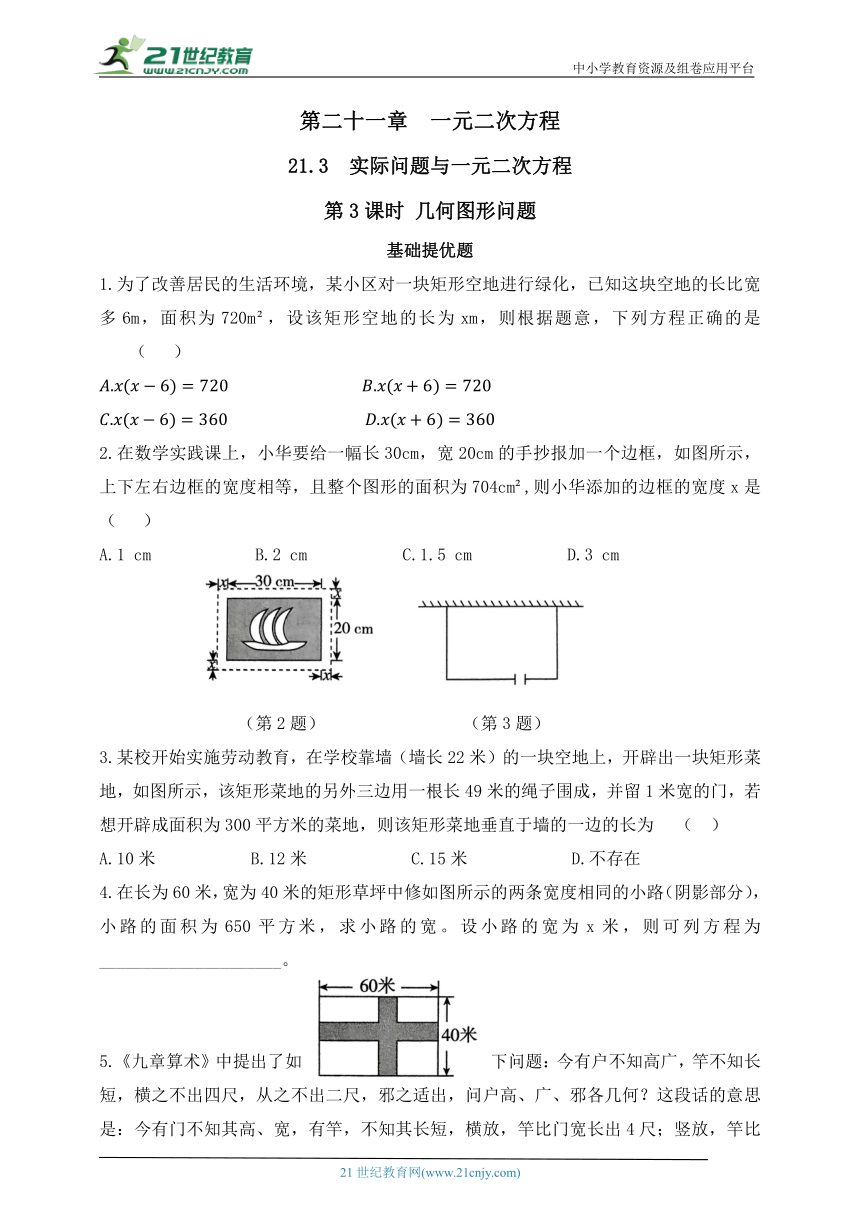 | |
| 格式 | docx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:19:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第3课时 几何图形问题
基础提优题
1.为了改善居民的生活环境,某小区对一块矩形空地进行绿化,已知这块空地的长比宽多6m,面积为720m ,设该矩形空地的长为xm,则根据题意,下列方程正确的是 ( )
2.在数学实践课上,小华要给一幅长30cm,宽20cm的手抄报加一个边框,如图所示,上下左右边框的宽度相等,且整个图形的面积为704cm ,则小华添加的边框的宽度x是( )
A.1 cm B.2 cm C.1.5 cm D.3 cm
(第2题) (第3题)
3.某校开始实施劳动教育,在学校靠墙(墙长22米)的一块空地上,开辟出一块矩形菜地,如图所示,该矩形菜地的另外三边用一根长49米的绳子围成,并留1米宽的门,若想开辟成面积为300平方米的菜地,则该矩形菜地垂直于墙的一边的长为 ( )
A.10米 B.12米 C.15米 D.不存在
4.在长为60米,宽为40米的矩形草坪中修如图所示的两条宽度相同的小路(阴影部分),小路的面积为650平方米,求小路的宽。设小路的宽为x米,则可列方程为_____________________。
5.《九章算术》中提出了如下问题:今有户不知高广,竿不知长短,横之不出四尺,从之不出二尺,邪之适出,问户高、广、邪各几何?这段话的意思是:今有门不知其高、宽,有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线的长恰好相等。问门高、宽和对角线的长各是多少?则该问题中的门高是___________尺。
6.如图,一块矩形铁皮的长为10cm,宽为8cm,现在它的四个角上剪去四个相同的小正方形,做成底面积为24cm 的无盖的长方体盒子,求剪去的小正方形的边长。
综合应用题。
7.如图,矩形ABCD是由三个矩形拼接成的。如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为 ( )
A.7 B.6 C.5 D.4
(第7题) (第8题)
8.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草。如图所示,要使种植花草的面积为864m ,那么小道的宽度应是( )
A.1 m B.2 m C.2.5 m D.3 m
9.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,现有动点P从点A出发,沿线段AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动,如果点P的速度是1cm/s,点Q的速度是2cm/s,P,Q两点同时出发,当有一点到达所在线段的端点时,另一点也停止运动,设运动时间为ts,当t=__________时,PQ平分△ABC的面积。
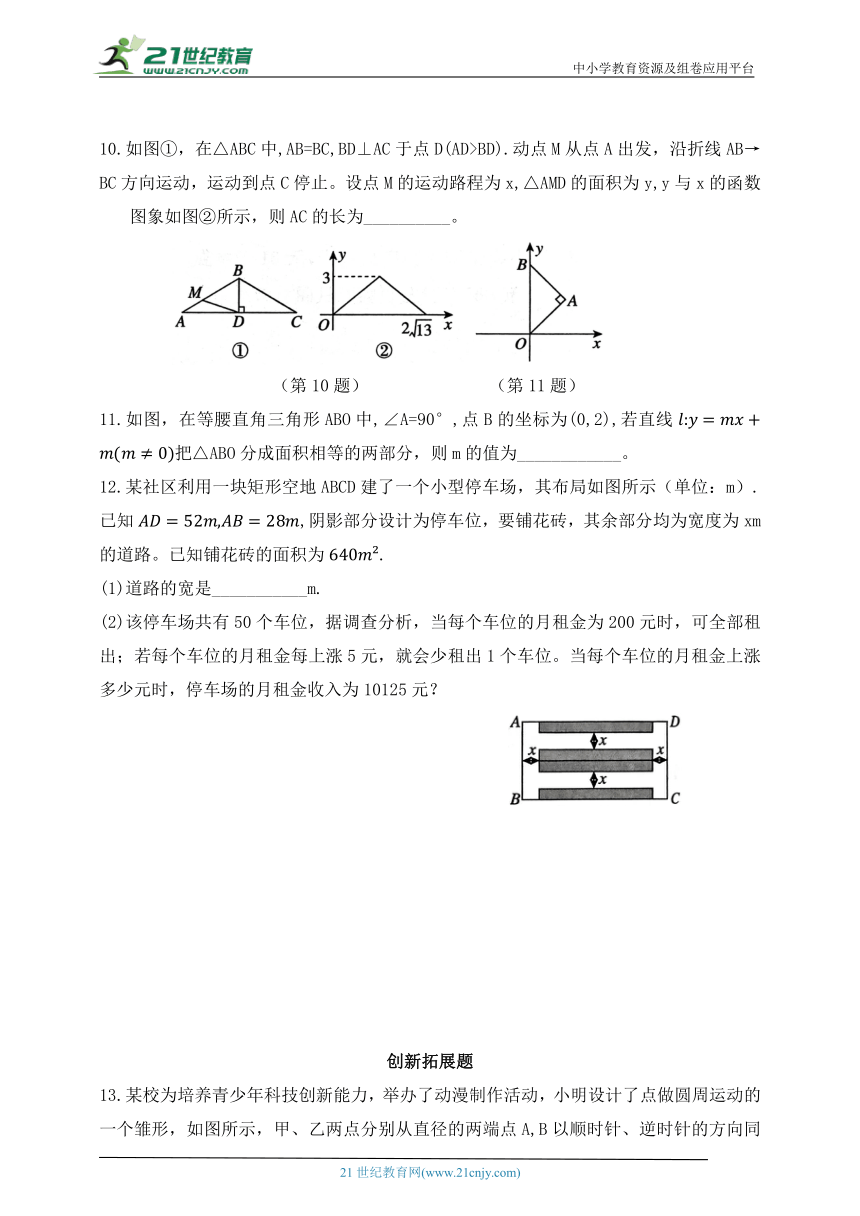
10.如图①,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从点A出发,沿折线AB→BC方向运动,运动到点C停止。设点M的运动路程为x,△AMD的面积为y,y与x的函数 图象如图②所示,则AC的长为__________。
(第10题) (第11题)
11.如图,在等腰直角三角形ABO中,∠A=90°,点B的坐标为(0,2),若直线把△ABO分成面积相等的两部分,则m的值为____________。
12.某社区利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示(单位:m).已知,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为xm的道路。已知铺花砖的面积为.
(1)道路的宽是___________m.
(2)该停车场共有50个车位,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为10125元?
创新拓展题
13.某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A,B以顺时针、逆时针的方向同时做圆周运动,甲运动的路程(cm)与时间(s)满足关系式:,乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
参考答案
1.A 2.A 3.C 4.4 5. 8
6.【解】设剪去的小正方形的边长为xcm,则无盖长方体盒子的底面长为,宽为,
依题意,得,解得x=2或x=7(不合题意,舍去)。
∴剪去的小正方形的边长为2cm.
7.B 8.B
9.2 【点拨】根据题意得AP=tcm,CQ=2tcm,∴PC=(8-t)cm.
由题易知0<t≤3.
∵PQ平分△ABC的面积,∴,即,
即,整理,得,解得(舍去).∴当t=2时,PQ平分△ABC的面积。
10.6 【点拨】由题图②知,。
又∵AB=BC,∴AB=BC=.
∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°.∴AD +BD =AB =13①.
由题意可得,当点M运动到点B时,△AMD的面积最大,最大为3,
∴AD.BD=3,∴AD·BD=6②.
①+2×②,得(负值已舍去).∴.
将其代入②,得,解得或.
【点拨】∵,∴一次函数一定过点(-1,0).∵△ABO是等腰直角三角形,∠A=90°,且点B的坐标为(0,2).∴易得点A的坐标为(1,1).如图①,当直线经过点A(1,1)时,显然,要使直线把△ABO分成面积相等的两部分,必然如图②所示,其中,且OC<OB,即解得
∴直线AB与直线交点D的坐标为.又BC=2-m,△DBC的高即为点D的横坐标,∴,解得(舍去)或.
12.【解】(1)6
(2)设当每个车位的月租金上涨a元时,停车场的月租金收入为10125元,
根据题意,得,
整理,得,解得
答:当每个车位的月租金上涨25元时,停车场的月租金收入为10125元。
13.【解】(1)当t=4时,故甲运动4s后的路程是14cm.
(2)由题图可知,甲、乙第一次相遇时走过的路程和为21cm,甲走过的路程为乙走过的路程为4tcm,则,解得t=3或t=-14(不合题意,舍去),故甲、乙从开始运动到第一次相遇时,它们运动了3s.
(3)由题图可知,甲、乙第二次相遇时走过的路程和为三个半圆:3×21=63(cm),则,解得t=7或t=-18(不合题意,舍去),故甲、乙从开始运动到第二次相遇时,它们运动了7s.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章 一元二次方程
21.3 实际问题与一元二次方程
第3课时 几何图形问题
基础提优题
1.为了改善居民的生活环境,某小区对一块矩形空地进行绿化,已知这块空地的长比宽多6m,面积为720m ,设该矩形空地的长为xm,则根据题意,下列方程正确的是 ( )
2.在数学实践课上,小华要给一幅长30cm,宽20cm的手抄报加一个边框,如图所示,上下左右边框的宽度相等,且整个图形的面积为704cm ,则小华添加的边框的宽度x是( )
A.1 cm B.2 cm C.1.5 cm D.3 cm
(第2题) (第3题)
3.某校开始实施劳动教育,在学校靠墙(墙长22米)的一块空地上,开辟出一块矩形菜地,如图所示,该矩形菜地的另外三边用一根长49米的绳子围成,并留1米宽的门,若想开辟成面积为300平方米的菜地,则该矩形菜地垂直于墙的一边的长为 ( )
A.10米 B.12米 C.15米 D.不存在
4.在长为60米,宽为40米的矩形草坪中修如图所示的两条宽度相同的小路(阴影部分),小路的面积为650平方米,求小路的宽。设小路的宽为x米,则可列方程为_____________________。
5.《九章算术》中提出了如下问题:今有户不知高广,竿不知长短,横之不出四尺,从之不出二尺,邪之适出,问户高、广、邪各几何?这段话的意思是:今有门不知其高、宽,有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线的长恰好相等。问门高、宽和对角线的长各是多少?则该问题中的门高是___________尺。
6.如图,一块矩形铁皮的长为10cm,宽为8cm,现在它的四个角上剪去四个相同的小正方形,做成底面积为24cm 的无盖的长方体盒子,求剪去的小正方形的边长。
综合应用题。
7.如图,矩形ABCD是由三个矩形拼接成的。如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为 ( )
A.7 B.6 C.5 D.4
(第7题) (第8题)
8.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草。如图所示,要使种植花草的面积为864m ,那么小道的宽度应是( )
A.1 m B.2 m C.2.5 m D.3 m
9.如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,现有动点P从点A出发,沿线段AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动,如果点P的速度是1cm/s,点Q的速度是2cm/s,P,Q两点同时出发,当有一点到达所在线段的端点时,另一点也停止运动,设运动时间为ts,当t=__________时,PQ平分△ABC的面积。
10.如图①,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从点A出发,沿折线AB→BC方向运动,运动到点C停止。设点M的运动路程为x,△AMD的面积为y,y与x的函数 图象如图②所示,则AC的长为__________。
(第10题) (第11题)
11.如图,在等腰直角三角形ABO中,∠A=90°,点B的坐标为(0,2),若直线把△ABO分成面积相等的两部分,则m的值为____________。
12.某社区利用一块矩形空地ABCD建了一个小型停车场,其布局如图所示(单位:m).已知,阴影部分设计为停车位,要铺花砖,其余部分均为宽度为xm的道路。已知铺花砖的面积为.
(1)道路的宽是___________m.
(2)该停车场共有50个车位,据调查分析,当每个车位的月租金为200元时,可全部租出;若每个车位的月租金每上涨5元,就会少租出1个车位。当每个车位的月租金上涨多少元时,停车场的月租金收入为10125元?
创新拓展题
13.某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A,B以顺时针、逆时针的方向同时做圆周运动,甲运动的路程(cm)与时间(s)满足关系式:,乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
参考答案
1.A 2.A 3.C 4.4 5. 8
6.【解】设剪去的小正方形的边长为xcm,则无盖长方体盒子的底面长为,宽为,
依题意,得,解得x=2或x=7(不合题意,舍去)。
∴剪去的小正方形的边长为2cm.
7.B 8.B
9.2 【点拨】根据题意得AP=tcm,CQ=2tcm,∴PC=(8-t)cm.
由题易知0<t≤3.
∵PQ平分△ABC的面积,∴,即,
即,整理,得,解得(舍去).∴当t=2时,PQ平分△ABC的面积。
10.6 【点拨】由题图②知,。
又∵AB=BC,∴AB=BC=.
∵AB=BC,BD⊥AC,∴AC=2AD,∠ADB=90°.∴AD +BD =AB =13①.
由题意可得,当点M运动到点B时,△AMD的面积最大,最大为3,
∴AD.BD=3,∴AD·BD=6②.
①+2×②,得(负值已舍去).∴.
将其代入②,得,解得或.
【点拨】∵,∴一次函数一定过点(-1,0).∵△ABO是等腰直角三角形,∠A=90°,且点B的坐标为(0,2).∴易得点A的坐标为(1,1).如图①,当直线经过点A(1,1)时,显然,要使直线把△ABO分成面积相等的两部分,必然如图②所示,其中,且OC<OB,即解得
∴直线AB与直线交点D的坐标为.又BC=2-m,△DBC的高即为点D的横坐标,∴,解得(舍去)或.
12.【解】(1)6
(2)设当每个车位的月租金上涨a元时,停车场的月租金收入为10125元,
根据题意,得,
整理,得,解得
答:当每个车位的月租金上涨25元时,停车场的月租金收入为10125元。
13.【解】(1)当t=4时,故甲运动4s后的路程是14cm.
(2)由题图可知,甲、乙第一次相遇时走过的路程和为21cm,甲走过的路程为乙走过的路程为4tcm,则,解得t=3或t=-14(不合题意,舍去),故甲、乙从开始运动到第一次相遇时,它们运动了3s.
(3)由题图可知,甲、乙第二次相遇时走过的路程和为三个半圆:3×21=63(cm),则,解得t=7或t=-18(不合题意,舍去),故甲、乙从开始运动到第二次相遇时,它们运动了7s.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
