21.1 一元二次方程 同步练习(含答案)
文档属性
| 名称 | 21.1 一元二次方程 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:20:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十一章 一元二次方程
21.1 一元二次方程
基础提优题
1.下列方程:③;⑥(中,属于一元二次方程的是( )
A.①和② B.②和⑤ C.③和④ D.③和⑥
2.把方程化成 的形式,则a,b,c的值分别是 ( )
A. 1,-2,-3 B. 1,-2,-6 C. 1,-2, 3 D. 1,-2,6
3.若是一元二次方程的一个根,则m的值为( )
A.-1或2 B.-1 C. 2 D.0
4.我国的乒乓球“梦之队”在2024年巴黎奥运赛场上大放异彩,奥运会乒乓球比赛的第一阶段是团体赛,赛制为单循环赛(每两队之间都赛一场)。计划分为4组,每组安排28场比赛,设每组邀请x个球队参加比赛,则可列方程为( )
5.已知关于x的方程是一元二次方程,则k的值应为_________。
6.若m是关于x的方程 2的解,则代数式 的值是____________。
7.已知一个一元二次方程有一个根是1,且它的一次项系数是-3,写出一个符合要求的方程:_____________。
8.如图为长20m,宽15 m的矩形空地,现计划要在中间修建三条等宽的小道,其余面积种植绿植,种植面积为200 m ,若设小道的宽为x m,则根据题意,可列方程为____________。
综合应用题
9.关于x的一元二次方程16x+1化为一般形式后不含一次项,则a 的值为 ( )
A. 0 B. ±4 C. 4 D.-4
10.下表是代数式 的值的情况,根据表格数据,可知方程 的根是( )
… -3 -2 -1 0 1 2 3 4 …
… 12 6 2 0 0 2 6 12 …
, ,
, ,
11.若一元二次方程 化为一般形式后为 ,则一次函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12. 若方程 中 a,b,c 满足4a+2b+c=0和4a-2b+c=0,则该方程的根是 ( )
A. 1,0 B. 1,-1 C.-1,0 D. 2,-2
13.若关于x的一元二次方程 (a≠0)有一根为x=2024,则一元二次方程 必有一根为( )
A. x=2023 B. x=2024 C. x=2025 D. x=2026
14.为提高公司经济效益,某公司决定对一种电子产品进行降价促销,根据市场调查,若这种电子产品的销售单价定为200元时,则每天可售出300个;若销售单价每降低1元,则每天可多售出5个。已知每个电子产品的固定成本为100元,当这种电子产品降价后的销售单价为多少元时,公司每天可获利32 000元?若设降价后的销售单价为x元,则可列方程为___________________。
15.已知关于x 的一元二次方程 ,其中a,b,c分别是△ABC三边的长,若x=-1是方程的根,则△ABC是____________三角形。
16. 若两个不同的方程 和 m=0有公共根,则常数m的值是_____________。
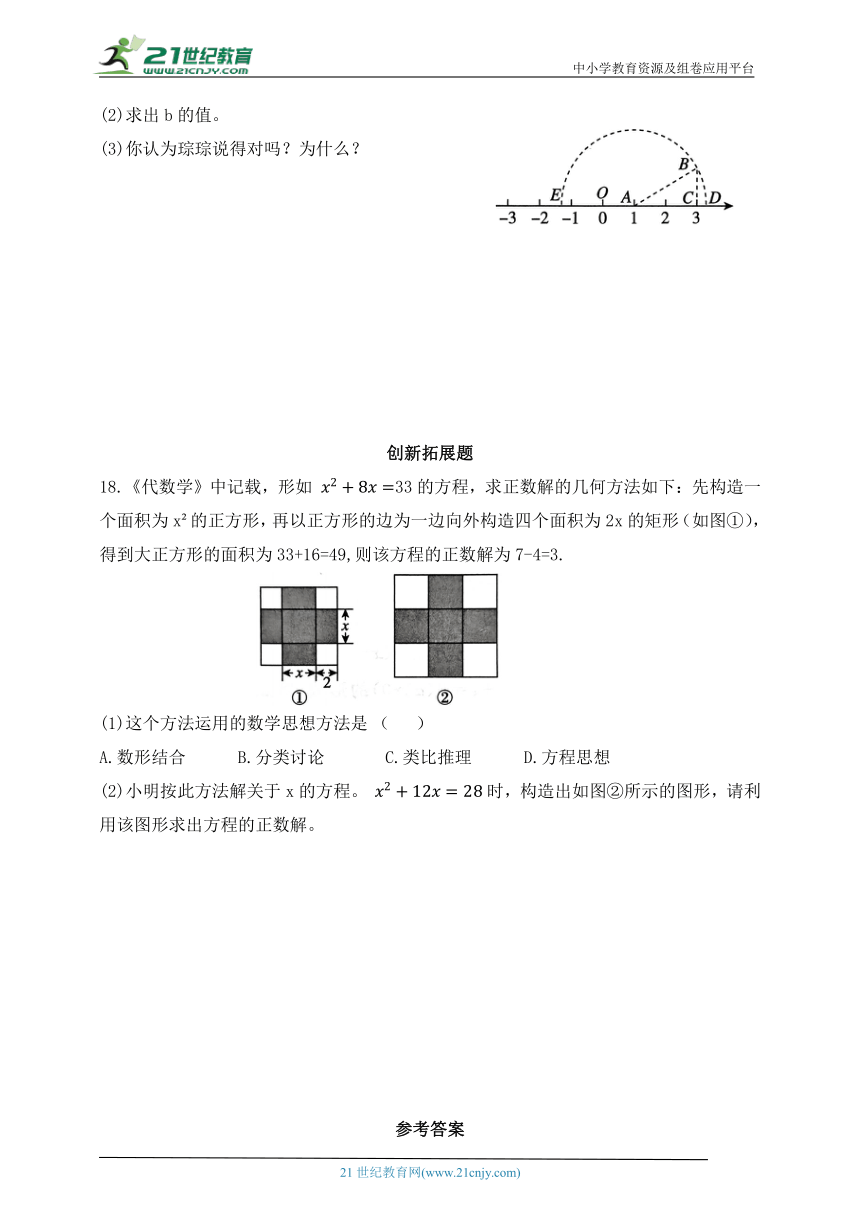
17.如图,点O为数轴原点,点A与点C表示的数分别为1和3,宸宸在数轴上以C为直角顶点作Rt△ABC,BC=1,再以A为圆心,AB长为半径画弧,交数轴于D,E两点。莲莲说:“若点D,E分别表示数m,n,我发现x=m是一元二次方程 0的一个根。”琮琮说:“x=n一定不是此方程的根。”
(1)求出m,n的值。
(2)求出b的值。
(3)你认为琮琮说得对吗?为什么?
创新拓展题
18.《代数学》中记载,形如 33的方程,求正数解的几何方法如下:先构造一个面积为x 的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形(如图①),得到大正方形的面积为33+16=49,则该方程的正数解为7-4=3.
(1)这个方法运用的数学思想方法是 ( )
A.数形结合 B.分类讨论 C.类比推理 D.方程思想
(2)小明按此方法解关于x的方程。 时,构造出如图②所示的图形,请利用该图形求出方程的正数解。
参考答案
1. C 2. D 3. B 4. D 5.-3 6.-1
(答案不唯一) 【点拨】由题意可设 3x+c=0,将x=1代入 ,得a-3+c=0,∴a+c=3.∴该方程可为
8. 9. D 10. C
11. D 【点拨】一元二次方程 化为一般形式后为 ∵一元二次方程 化为一般形式后为,解得
∴.∴一次函数 的图象经过第一、二、三象限,不经过第四象限。故选D.
12. D 13. C
14..【点拨】由题可知,销售一个电子产品的利润为(x-100)元。
∵若该电子产品的销售单价定为200元时,则每天可售出300个;若销售单价每降低1元,则每天可多售出5个;
∴销售电子产品的个数为个。
∴根据题意可列方程为.
15.等腰 【点拨】把x=-1代入0,得,所以,所以△ABC为等腰三角形。
16.-2【点拨】设方程和的公共根为t,
则①-②,得.
如果m=1,那么两个方程均为 ,不符合题意;
如果m≠1,那么t=1,把t=1代入①,得1+m+1=0,解得m=-2.
17.【解】(1)在Rt△ABC中,∵BC=1,AC=3-1=2,∴AB=,, ,,∴点D表示的数为,即,点E表示的数为,
即
(2)把代入方程,得1)b-4=0,解得b=-2.
(3)琮琮说得不对。理由如下:由(2)可知一元二次方程为 2x-4=0.把 代入,得 , 一定是此方程的根。
18.【解】(1)A
(2)构造一个面积为x 的正方形,再以正方形的边为一边向外构造四个面积为3x的矩形,
得到大正方形的面积为,则该方程的正数解为8-2×3=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章 一元二次方程
21.1 一元二次方程
基础提优题
1.下列方程:③;⑥(中,属于一元二次方程的是( )
A.①和② B.②和⑤ C.③和④ D.③和⑥
2.把方程化成 的形式,则a,b,c的值分别是 ( )
A. 1,-2,-3 B. 1,-2,-6 C. 1,-2, 3 D. 1,-2,6
3.若是一元二次方程的一个根,则m的值为( )
A.-1或2 B.-1 C. 2 D.0
4.我国的乒乓球“梦之队”在2024年巴黎奥运赛场上大放异彩,奥运会乒乓球比赛的第一阶段是团体赛,赛制为单循环赛(每两队之间都赛一场)。计划分为4组,每组安排28场比赛,设每组邀请x个球队参加比赛,则可列方程为( )
5.已知关于x的方程是一元二次方程,则k的值应为_________。
6.若m是关于x的方程 2的解,则代数式 的值是____________。
7.已知一个一元二次方程有一个根是1,且它的一次项系数是-3,写出一个符合要求的方程:_____________。
8.如图为长20m,宽15 m的矩形空地,现计划要在中间修建三条等宽的小道,其余面积种植绿植,种植面积为200 m ,若设小道的宽为x m,则根据题意,可列方程为____________。
综合应用题
9.关于x的一元二次方程16x+1化为一般形式后不含一次项,则a 的值为 ( )
A. 0 B. ±4 C. 4 D.-4
10.下表是代数式 的值的情况,根据表格数据,可知方程 的根是( )
… -3 -2 -1 0 1 2 3 4 …
… 12 6 2 0 0 2 6 12 …
, ,
, ,
11.若一元二次方程 化为一般形式后为 ,则一次函数 的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12. 若方程 中 a,b,c 满足4a+2b+c=0和4a-2b+c=0,则该方程的根是 ( )
A. 1,0 B. 1,-1 C.-1,0 D. 2,-2
13.若关于x的一元二次方程 (a≠0)有一根为x=2024,则一元二次方程 必有一根为( )
A. x=2023 B. x=2024 C. x=2025 D. x=2026
14.为提高公司经济效益,某公司决定对一种电子产品进行降价促销,根据市场调查,若这种电子产品的销售单价定为200元时,则每天可售出300个;若销售单价每降低1元,则每天可多售出5个。已知每个电子产品的固定成本为100元,当这种电子产品降价后的销售单价为多少元时,公司每天可获利32 000元?若设降价后的销售单价为x元,则可列方程为___________________。
15.已知关于x 的一元二次方程 ,其中a,b,c分别是△ABC三边的长,若x=-1是方程的根,则△ABC是____________三角形。
16. 若两个不同的方程 和 m=0有公共根,则常数m的值是_____________。
17.如图,点O为数轴原点,点A与点C表示的数分别为1和3,宸宸在数轴上以C为直角顶点作Rt△ABC,BC=1,再以A为圆心,AB长为半径画弧,交数轴于D,E两点。莲莲说:“若点D,E分别表示数m,n,我发现x=m是一元二次方程 0的一个根。”琮琮说:“x=n一定不是此方程的根。”
(1)求出m,n的值。
(2)求出b的值。
(3)你认为琮琮说得对吗?为什么?
创新拓展题
18.《代数学》中记载,形如 33的方程,求正数解的几何方法如下:先构造一个面积为x 的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形(如图①),得到大正方形的面积为33+16=49,则该方程的正数解为7-4=3.
(1)这个方法运用的数学思想方法是 ( )
A.数形结合 B.分类讨论 C.类比推理 D.方程思想
(2)小明按此方法解关于x的方程。 时,构造出如图②所示的图形,请利用该图形求出方程的正数解。
参考答案
1. C 2. D 3. B 4. D 5.-3 6.-1
(答案不唯一) 【点拨】由题意可设 3x+c=0,将x=1代入 ,得a-3+c=0,∴a+c=3.∴该方程可为
8. 9. D 10. C
11. D 【点拨】一元二次方程 化为一般形式后为 ∵一元二次方程 化为一般形式后为,解得
∴.∴一次函数 的图象经过第一、二、三象限,不经过第四象限。故选D.
12. D 13. C
14..【点拨】由题可知,销售一个电子产品的利润为(x-100)元。
∵若该电子产品的销售单价定为200元时,则每天可售出300个;若销售单价每降低1元,则每天可多售出5个;
∴销售电子产品的个数为个。
∴根据题意可列方程为.
15.等腰 【点拨】把x=-1代入0,得,所以,所以△ABC为等腰三角形。
16.-2【点拨】设方程和的公共根为t,
则①-②,得.
如果m=1,那么两个方程均为 ,不符合题意;
如果m≠1,那么t=1,把t=1代入①,得1+m+1=0,解得m=-2.
17.【解】(1)在Rt△ABC中,∵BC=1,AC=3-1=2,∴AB=,, ,,∴点D表示的数为,即,点E表示的数为,
即
(2)把代入方程,得1)b-4=0,解得b=-2.
(3)琮琮说得不对。理由如下:由(2)可知一元二次方程为 2x-4=0.把 代入,得 , 一定是此方程的根。
18.【解】(1)A
(2)构造一个面积为x 的正方形,再以正方形的边为一边向外构造四个面积为3x的矩形,
得到大正方形的面积为,则该方程的正数解为8-2×3=2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
