【新课预习衔接】6.1几何图形(培优卷.含解析)-2025-2026学年七年级上册数学人教版(2024)
文档属性
| 名称 | 【新课预习衔接】6.1几何图形(培优卷.含解析)-2025-2026学年七年级上册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 273.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 11:53:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
新课预习衔接 几何图形
一.选择题(共5小题)
1.(2024秋 南海区期中)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“爱大沥讲文明”,把它折成正方体后,与“大”相对的字是( )
A.沥 B.讲 C.文 D.明
2.(2024秋 福田区期中)直升飞机螺旋桨一般由4片桨叶组成,直升飞机起飞时,螺旋桨旋转时向下推动空气,即向下施加一个作用力,直升飞机获得竖直向上的力,使得飞机能悬浮在空中.若把螺旋桨看作一条线段,旋转形成的痕迹体现了( )
A.面动成体 B.线动成面
C.点动成线 D.面面相交成线
3.(2024秋 宝安区校级期中)如图为一个乐高积木示意图,这个几何体的左视图为( )
A. B.
C. D.
4.(2024 十堰模拟)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
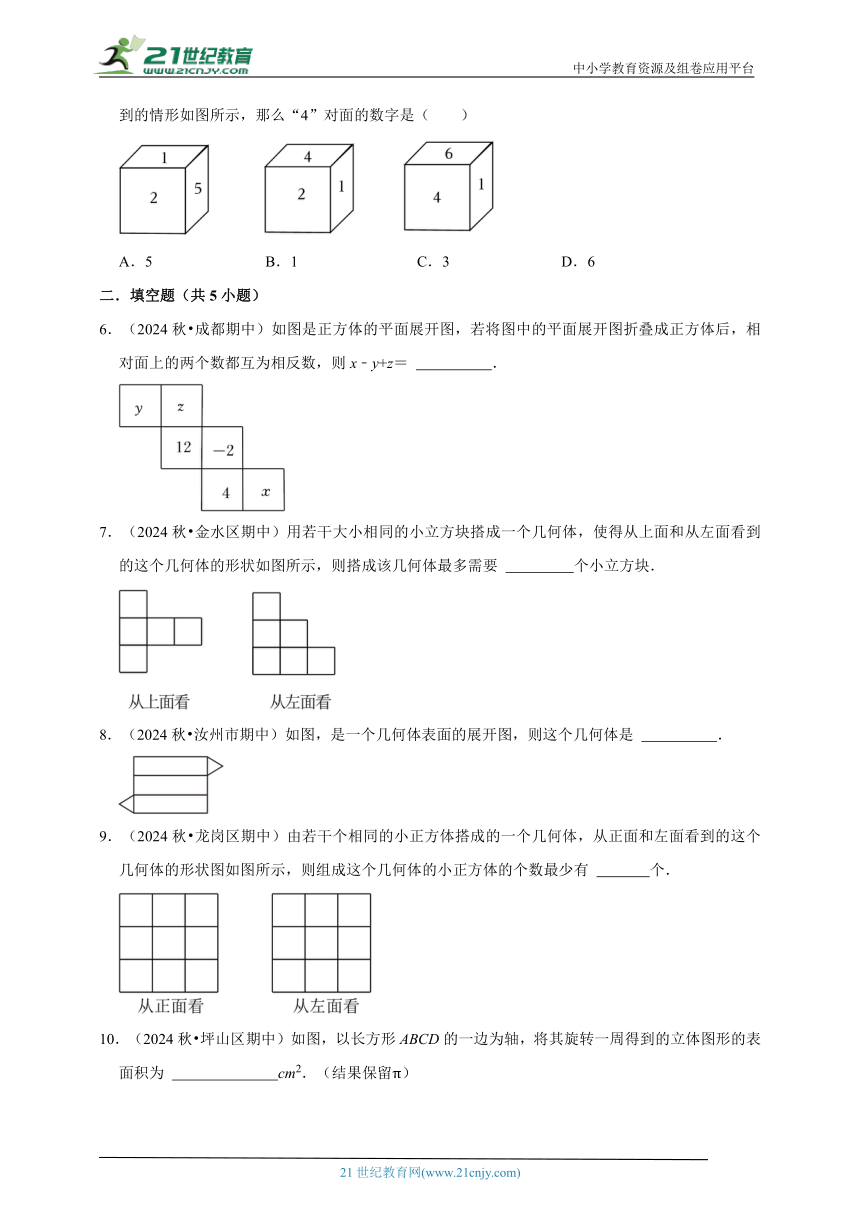
5.(2024秋 金水区期中)一个小立方块的六个面分别写着1,2,3,4,5,6,从三个不同方向看到的情形如图所示,那么“4”对面的数字是( )
A.5 B.1 C.3 D.6
二.填空题(共5小题)
6.(2024秋 成都期中)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,则x﹣y+z= .
7.(2024秋 金水区期中)用若干大小相同的小立方块搭成一个几何体,使得从上面和从左面看到的这个几何体的形状如图所示,则搭成该几何体最多需要 个小立方块.
8.(2024秋 汝州市期中)如图,是一个几何体表面的展开图,则这个几何体是 .
9.(2024秋 龙岗区期中)由若干个相同的小正方体搭成的一个几何体,从正面和左面看到的这个几何体的形状图如图所示,则组成这个几何体的小正方体的个数最少有 个.
10.(2024秋 坪山区期中)如图,以长方形ABCD的一边为轴,将其旋转一周得到的立体图形的表面积为 cm2.(结果保留π)
三.解答题(共5小题)
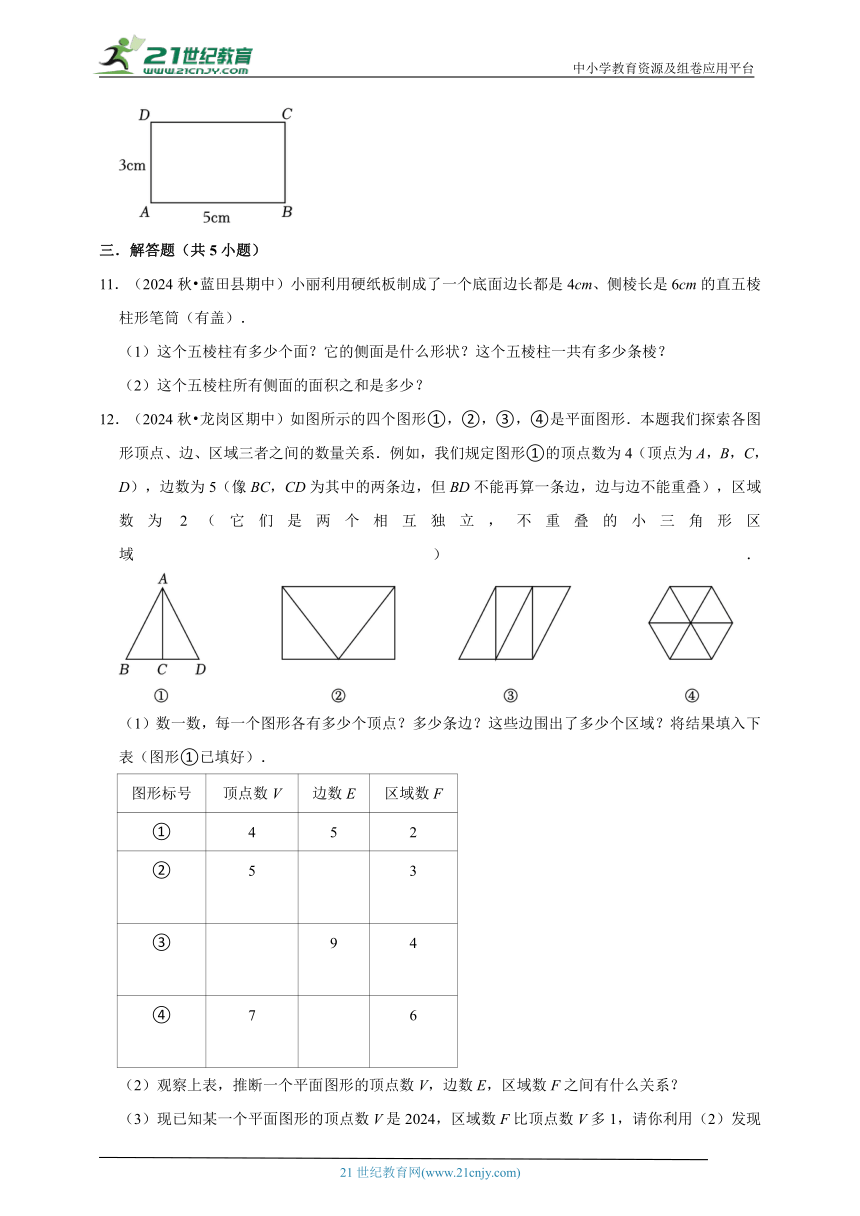
11.(2024秋 蓝田县期中)小丽利用硬纸板制成了一个底面边长都是4cm、侧棱长是6cm的直五棱柱形笔筒(有盖).
(1)这个五棱柱有多少个面?它的侧面是什么形状?这个五棱柱一共有多少条棱?
(2)这个五棱柱所有侧面的面积之和是多少?
12.(2024秋 龙岗区期中)如图所示的四个图形①,②,③,④是平面图形.本题我们探索各图形顶点、边、区域三者之间的数量关系.例如,我们规定图形①的顶点数为4(顶点为A,B,C,D),边数为5(像BC,CD为其中的两条边,但BD不能再算一条边,边与边不能重叠),区域数为2(它们是两个相互独立,不重叠的小三角形区域).
(1)数一数,每一个图形各有多少个顶点?多少条边?这些边围出了多少个区域?将结果填入下表(图形①已填好).
图形标号 顶点数V 边数E 区域数F
① 4 5 2
② 5
3
③
9 4
④ 7
6
(2)观察上表,推断一个平面图形的顶点数V,边数E,区域数F之间有什么关系?
(3)现已知某一个平面图形的顶点数V是2024,区域数F比顶点数V多1,请你利用(2)发现的结论,确定这个图形的边数E是多少?
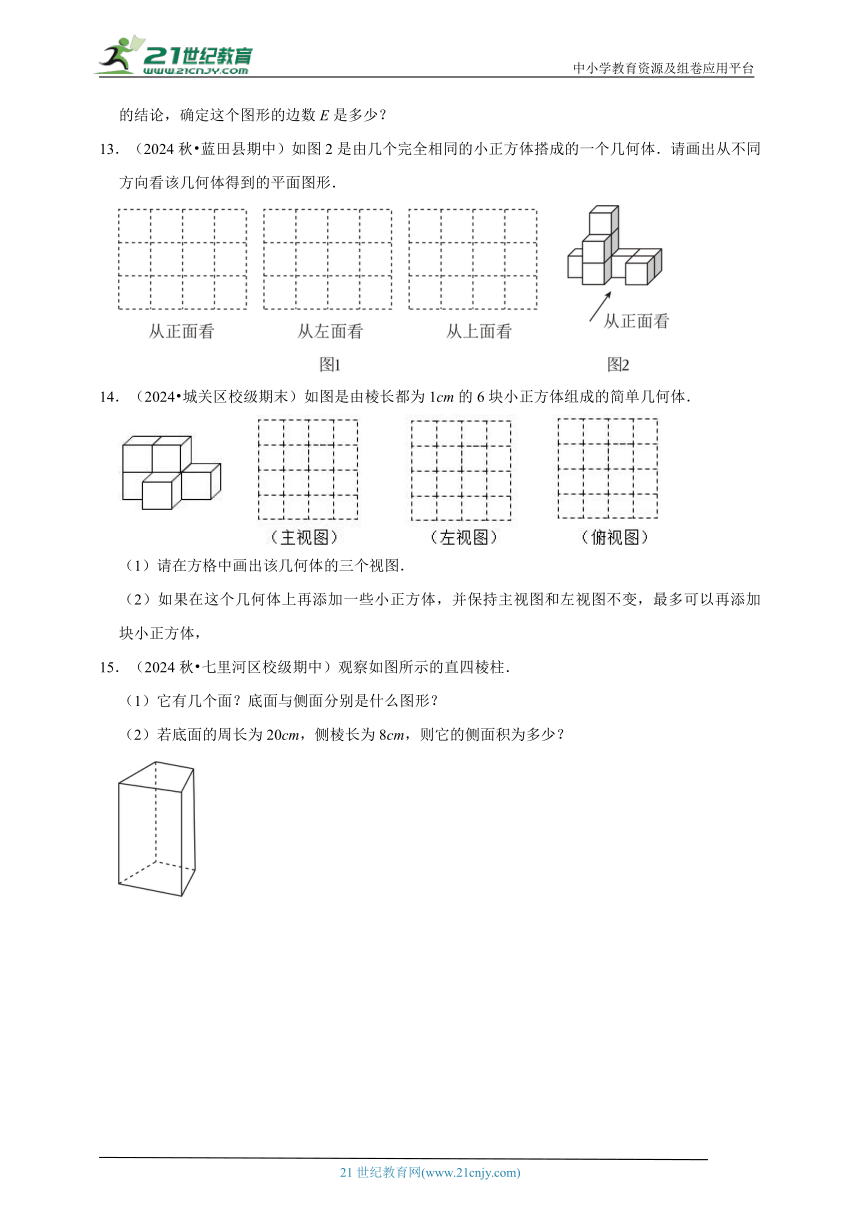
13.(2024秋 蓝田县期中)如图2是由几个完全相同的小正方体搭成的一个几何体.请画出从不同方向看该几何体得到的平面图形.
14.(2024 城关区校级期末)如图是由棱长都为1cm的6块小正方体组成的简单几何体.
(1)请在方格中画出该几何体的三个视图.
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 块小正方体,
15.(2024秋 七里河区校级期中)观察如图所示的直四棱柱.
(1)它有几个面?底面与侧面分别是什么图形?
(2)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
新课预习衔接 几何图形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南海区期中)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“爱大沥讲文明”,把它折成正方体后,与“大”相对的字是( )
A.沥 B.讲 C.文 D.明
【考点】专题:正方体相对两个面上的文字.2024
【专题】展开与折叠;空间观念.
【答案】B
【分析】对于正方体的平面展开图中相对的面一定相隔一个小正方形,据此作答.
【解答】解:把它折成正方体后,与“大”相对的字是“讲”.
故选:B.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2024秋 福田区期中)直升飞机螺旋桨一般由4片桨叶组成,直升飞机起飞时,螺旋桨旋转时向下推动空气,即向下施加一个作用力,直升飞机获得竖直向上的力,使得飞机能悬浮在空中.若把螺旋桨看作一条线段,旋转形成的痕迹体现了( )
A.面动成体 B.线动成面
C.点动成线 D.面面相交成线
【考点】点、线、面、体.2024
【专题】几何图形;几何直观.
【答案】B
【分析】根据点、线、面、体的关系解答即可.
【解答】解:若把螺旋桨看作一条线段,旋转形成的痕迹体现了线动成面.
故选:B.
【点评】本题考查了点、线、面、体的关系,解题的关键是明确点动成线,线动成面,面动成体.
3.(2024秋 宝安区校级期中)如图为一个乐高积木示意图,这个几何体的左视图为( )
A. B.
C. D.
【考点】简单组合体的三视图.2024
【专题】投影与视图;空间观念.
【答案】C
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解答】解:从左面看,可得选项C的图形.
故选:C.
【点评】本题主要考查简单组合体的三视图,熟练掌握简单组合体的三视图是解题的关键.
4.(2024 十堰模拟)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
【考点】简单几何体的三视图.2024
【专题】投影与视图;空间观念.
【答案】A
【分析】根据三视图的定义求解即可.
【解答】解:这个几何体的主视图与左视图相同,俯视图与主视图和左视图不相同.
故选:A.
【点评】此题主要考查了简单组合体的三视图,正确把握观察的角度是解题关键.
5.(2024秋 金水区期中)一个小立方块的六个面分别写着1,2,3,4,5,6,从三个不同方向看到的情形如图所示,那么“4”对面的数字是( )
A.5 B.1 C.3 D.6
【考点】专题:正方体相对两个面上的文字.2024
【专题】展开与折叠;空间观念.
【答案】A
【分析】根据正方体表面展开图的判断“邻面”和“对面”即可.
【解答】解:由三个几何体可知,与数字1所在的面相邻的面上数字是2,5,4,6,
故数字1对面的数字是3,
由第二个和第三个正方体可知,与数字4所在的面相邻的面上数字是1、2、6,
即与数字4所在的面相邻的面上数字是1、2、3,6,
因此,“4”对面的数字是“5”.
故选:A.
【点评】本题考查了正方体对面的数字,判断出“邻面”“对面”是正确解答的关键.
二.填空题(共5小题)
6.(2024秋 成都期中)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,则x﹣y+z= ﹣18 .
【考点】专题:正方体相对两个面上的文字;相反数.2024
【专题】展开与折叠;空间观念.
【答案】﹣18.
【分析】根据相对面上的两个数互为相反数,则“z”与面“4”相对,面“y”与面“﹣2”相对,“x”与面“12”相对,得出x,y,z,再代入求值即可.
【解答】解:∵“z”与面“4”相对,面“y”与面“﹣2”相对,“x”与面“12”相对,
又∵相对面上的两个数互为相反数,
∴x=﹣12,y=2,z=﹣4,
∴x﹣y+z=﹣12﹣2+(﹣4)=﹣18.
【点评】本题考查相反数,正方体的相对面上的文字,掌握正方体的相对面,有理数的加减是关键.
7.(2024秋 金水区期中)用若干大小相同的小立方块搭成一个几何体,使得从上面和从左面看到的这个几何体的形状如图所示,则搭成该几何体最多需要 10 个小立方块.
【考点】由三视图判断几何体.2024
【专题】投影与视图;空间观念.
【答案】10.
【分析】在俯视图标出小正方体的个数即可解答.
【解答】解:如图所示:
搭成该几何体最多需要小立方块:3+2+2+2+1=10(个).
故答案为:10.
【点评】本题考查了由三视图判断几何体,理解视图的定义,掌握三视图的画法及形状是正确解答的前提.
8.(2024秋 汝州市期中)如图,是一个几何体表面的展开图,则这个几何体是 三棱柱 .
【考点】几何体的展开图.2024
【专题】展开与折叠;空间观念.
【答案】三棱柱.
【分析】根据侧面为n个长方形,底边为n边形,原几何体为n棱柱,依此即可求解.
【解答】解:三棱柱的侧面由3个长方形组成,底面由2个三角形组成,故原几何体为三棱柱.
故答案为:三棱柱.
【点评】本题考查了几何体的展开图,熟记几何体展开图的形状是解题关键.
9.(2024秋 龙岗区期中)由若干个相同的小正方体搭成的一个几何体,从正面和左面看到的这个几何体的形状图如图所示,则组成这个几何体的小正方体的个数最少有 9 个.
【考点】由三视图判断几何体.2024
【专题】投影与视图;空间观念.
【答案】9.
【分析】根据主视图、左视图的形状,画出需要小正方体个数最少时的俯视图,并标注所摆放的小正方体的个数即可.
【解答】解:需要小正方体个数最少时,从上面看的图形如图所示,其中数字表示该位置所摆放小正方体的个数,
因此需要的小正方体的个数最少为3+3+3=9(个),
故答案为:9.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法和形状是正确解答的关键.
10.(2024秋 坪山区期中)如图,以长方形ABCD的一边为轴,将其旋转一周得到的立体图形的表面积为 80π或48π cm2.(结果保留π)
【考点】几何体的表面积;列代数式;点、线、面、体.2024
【专题】几何图形;运算能力.
【答案】80π或48π.
【分析】根据面动成体可知得到的立体图形为圆柱;以不同的边为轴旋转一周,所得到的圆柱体的底面半径和高,根据圆柱体的表面积公式计算即可.
【解答】解:长方形绕着它的一边所在的直线旋转一周,得到的立体图形是圆柱,
绕着5cm的边为轴,旋转一周所得到的是底面半径为3cm,高为5cm的圆柱体,因此表面积为2π×3×5+π×32×2=48π(cm2),
绕着3cm的边为轴,旋转一周所得到的是底面半径为5cm,高为3cm的圆柱体,因此表面积为2π×5×3+π×52×2=80π(cm2);
故答案为:80π或48π.
【点评】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
三.解答题(共5小题)
11.(2024秋 蓝田县期中)小丽利用硬纸板制成了一个底面边长都是4cm、侧棱长是6cm的直五棱柱形笔筒(有盖).
(1)这个五棱柱有多少个面?它的侧面是什么形状?这个五棱柱一共有多少条棱?
(2)这个五棱柱所有侧面的面积之和是多少?
【考点】几何体的表面积;认识立体图形.2024
【专题】几何图形;几何直观.
【答案】(1)7,长方形,15;
(2)120cm2.
【分析】(1)根据五棱柱的构造特征即可解答;
(2)根据五棱柱的侧面都是长方形,面积为长乘宽,即可求出.
【解答】解:(1)这个五棱柱有7个面,它的侧面是长方形,这个五棱柱一共有15条棱.
(2)4×6×5=120(cm2)
答:这个五棱柱所有侧面的面积之和是120cm2.
【点评】本题考查了五棱柱的构造特征,明确五棱柱的构造特征是解答的关键.
12.(2024秋 龙岗区期中)如图所示的四个图形①,②,③,④是平面图形.本题我们探索各图形顶点、边、区域三者之间的数量关系.例如,我们规定图形①的顶点数为4(顶点为A,B,C,D),边数为5(像BC,CD为其中的两条边,但BD不能再算一条边,边与边不能重叠),区域数为2(它们是两个相互独立,不重叠的小三角形区域).
(1)数一数,每一个图形各有多少个顶点?多少条边?这些边围出了多少个区域?将结果填入下表(图形①已填好).
图形标号 顶点数V 边数E 区域数F
① 4 5 2
② 5
7
3
③
6
9 4
④ 7
12
6
(2)观察上表,推断一个平面图形的顶点数V,边数E,区域数F之间有什么关系?
(3)现已知某一个平面图形的顶点数V是2024,区域数F比顶点数V多1,请你利用(2)发现的结论,确定这个图形的边数E是多少?
【考点】认识平面图形;欧拉公式.2024
【专题】规律型;多边形与平行四边形;几何直观;运算能力.
【答案】(1)7,6,12;
(2)V+F=E+1;
(3)E=4048.
【分析】(1)根据各个图形的特征以及“顶点数”,“边数”,“区域”的意义进行解答即可;
(2)根据表格中“顶点数”,“边数”,“区域”之间的关系进行解答即可;
(3)根据(2)的结论进行计算即可.
【解答】解:(1)由题意可得,
故答案为:7,6,12;
(2)由(1)中的规律可得,
V+F=E+1;
(3)∵V=2024,区域数F比顶点数V多1,
∴F=V+1=2025,
∵V+F=E+1,
∴E=V+F﹣1=4048.
【点评】本题考查认识平面图形,理解一个平面图形的“顶点数”,“边数”,“区域”的意义是正确解答的关键.
13.(2024秋 蓝田县期中)如图2是由几个完全相同的小正方体搭成的一个几何体.请画出从不同方向看该几何体得到的平面图形.
【考点】简单组合体的三视图.2024
【专题】投影与视图;空间观念.
【答案】见解答.
【分析】根据从正面看的意义,从左面看的意义,从上面看的意义,画图即可.
【解答】解:根据题意,画图如下:
.
【点评】本题考查了从不同方向看,理解不同方向看的意义,是解题的关键.
14.(2024 城关区校级期末)如图是由棱长都为1cm的6块小正方体组成的简单几何体.
(1)请在方格中画出该几何体的三个视图.
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 2 块小正方体,
【考点】简单几何体的三视图.2024
【专题】投影与视图;空间观念.
【答案】(1)见解答;
(2)2.
【分析】(1)根据简单组合体三视图的画法画出相应的图形即可;
(2)在俯视图上相应位置备注出相应摆放的数目即可.
【解答】解:(1)该几何体的主视图、左视图和俯视图如下:
(2)在备注数字的位置加摆相应数量的小正方体,
所以最多可以添加2个,
故答案为:2.
【点评】本题考查简单组合体的三视图,理解视图的意义是正确解答的前提.
15.(2024秋 七里河区校级期中)观察如图所示的直四棱柱.
(1)它有几个面?底面与侧面分别是什么图形?
(2)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
【考点】几何体的表面积;认识立体图形.2024
【专题】展开与折叠;几何直观.
【答案】(1)6个面,底面为四边形,侧面为长方形;
(2)160cm2.
【分析】(1)根据直四棱柱的特征,即可得到答案;
(2)直棱柱的侧面积=底面周长×高,由此即可计算.
【解答】解:(1)由图可知:直四棱柱有6个面,底面为四边形,侧面为长方形;
(2)20×8=160(cm2),
答:直四棱柱的侧面积是160cm2.
【点评】本题考查几何体的表面积,认识立体图形,关键是掌握棱柱的概念,直棱柱侧面积的计算公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 几何图形
一.选择题(共5小题)
1.(2024秋 南海区期中)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“爱大沥讲文明”,把它折成正方体后,与“大”相对的字是( )
A.沥 B.讲 C.文 D.明
2.(2024秋 福田区期中)直升飞机螺旋桨一般由4片桨叶组成,直升飞机起飞时,螺旋桨旋转时向下推动空气,即向下施加一个作用力,直升飞机获得竖直向上的力,使得飞机能悬浮在空中.若把螺旋桨看作一条线段,旋转形成的痕迹体现了( )
A.面动成体 B.线动成面
C.点动成线 D.面面相交成线
3.(2024秋 宝安区校级期中)如图为一个乐高积木示意图,这个几何体的左视图为( )
A. B.
C. D.
4.(2024 十堰模拟)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
5.(2024秋 金水区期中)一个小立方块的六个面分别写着1,2,3,4,5,6,从三个不同方向看到的情形如图所示,那么“4”对面的数字是( )
A.5 B.1 C.3 D.6
二.填空题(共5小题)
6.(2024秋 成都期中)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,则x﹣y+z= .
7.(2024秋 金水区期中)用若干大小相同的小立方块搭成一个几何体,使得从上面和从左面看到的这个几何体的形状如图所示,则搭成该几何体最多需要 个小立方块.
8.(2024秋 汝州市期中)如图,是一个几何体表面的展开图,则这个几何体是 .
9.(2024秋 龙岗区期中)由若干个相同的小正方体搭成的一个几何体,从正面和左面看到的这个几何体的形状图如图所示,则组成这个几何体的小正方体的个数最少有 个.
10.(2024秋 坪山区期中)如图,以长方形ABCD的一边为轴,将其旋转一周得到的立体图形的表面积为 cm2.(结果保留π)
三.解答题(共5小题)
11.(2024秋 蓝田县期中)小丽利用硬纸板制成了一个底面边长都是4cm、侧棱长是6cm的直五棱柱形笔筒(有盖).
(1)这个五棱柱有多少个面?它的侧面是什么形状?这个五棱柱一共有多少条棱?
(2)这个五棱柱所有侧面的面积之和是多少?
12.(2024秋 龙岗区期中)如图所示的四个图形①,②,③,④是平面图形.本题我们探索各图形顶点、边、区域三者之间的数量关系.例如,我们规定图形①的顶点数为4(顶点为A,B,C,D),边数为5(像BC,CD为其中的两条边,但BD不能再算一条边,边与边不能重叠),区域数为2(它们是两个相互独立,不重叠的小三角形区域).
(1)数一数,每一个图形各有多少个顶点?多少条边?这些边围出了多少个区域?将结果填入下表(图形①已填好).
图形标号 顶点数V 边数E 区域数F
① 4 5 2
② 5
3
③
9 4
④ 7
6
(2)观察上表,推断一个平面图形的顶点数V,边数E,区域数F之间有什么关系?
(3)现已知某一个平面图形的顶点数V是2024,区域数F比顶点数V多1,请你利用(2)发现的结论,确定这个图形的边数E是多少?
13.(2024秋 蓝田县期中)如图2是由几个完全相同的小正方体搭成的一个几何体.请画出从不同方向看该几何体得到的平面图形.
14.(2024 城关区校级期末)如图是由棱长都为1cm的6块小正方体组成的简单几何体.
(1)请在方格中画出该几何体的三个视图.
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 块小正方体,
15.(2024秋 七里河区校级期中)观察如图所示的直四棱柱.
(1)它有几个面?底面与侧面分别是什么图形?
(2)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
新课预习衔接 几何图形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 南海区期中)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“爱大沥讲文明”,把它折成正方体后,与“大”相对的字是( )
A.沥 B.讲 C.文 D.明
【考点】专题:正方体相对两个面上的文字.2024
【专题】展开与折叠;空间观念.
【答案】B
【分析】对于正方体的平面展开图中相对的面一定相隔一个小正方形,据此作答.
【解答】解:把它折成正方体后,与“大”相对的字是“讲”.
故选:B.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2024秋 福田区期中)直升飞机螺旋桨一般由4片桨叶组成,直升飞机起飞时,螺旋桨旋转时向下推动空气,即向下施加一个作用力,直升飞机获得竖直向上的力,使得飞机能悬浮在空中.若把螺旋桨看作一条线段,旋转形成的痕迹体现了( )
A.面动成体 B.线动成面
C.点动成线 D.面面相交成线
【考点】点、线、面、体.2024
【专题】几何图形;几何直观.
【答案】B
【分析】根据点、线、面、体的关系解答即可.
【解答】解:若把螺旋桨看作一条线段,旋转形成的痕迹体现了线动成面.
故选:B.
【点评】本题考查了点、线、面、体的关系,解题的关键是明确点动成线,线动成面,面动成体.
3.(2024秋 宝安区校级期中)如图为一个乐高积木示意图,这个几何体的左视图为( )
A. B.
C. D.
【考点】简单组合体的三视图.2024
【专题】投影与视图;空间观念.
【答案】C
【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
【解答】解:从左面看,可得选项C的图形.
故选:C.
【点评】本题主要考查简单组合体的三视图,熟练掌握简单组合体的三视图是解题的关键.
4.(2024 十堰模拟)隋朝时期的青瓷高足盘是湖北省博物馆重要馆藏文物之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )
A.主视图与左视图相同 B.主视图与俯视图相同
C.左视图与俯视图相同 D.三种视图都相同
【考点】简单几何体的三视图.2024
【专题】投影与视图;空间观念.
【答案】A
【分析】根据三视图的定义求解即可.
【解答】解:这个几何体的主视图与左视图相同,俯视图与主视图和左视图不相同.
故选:A.
【点评】此题主要考查了简单组合体的三视图,正确把握观察的角度是解题关键.
5.(2024秋 金水区期中)一个小立方块的六个面分别写着1,2,3,4,5,6,从三个不同方向看到的情形如图所示,那么“4”对面的数字是( )
A.5 B.1 C.3 D.6
【考点】专题:正方体相对两个面上的文字.2024
【专题】展开与折叠;空间观念.
【答案】A
【分析】根据正方体表面展开图的判断“邻面”和“对面”即可.
【解答】解:由三个几何体可知,与数字1所在的面相邻的面上数字是2,5,4,6,
故数字1对面的数字是3,
由第二个和第三个正方体可知,与数字4所在的面相邻的面上数字是1、2、6,
即与数字4所在的面相邻的面上数字是1、2、3,6,
因此,“4”对面的数字是“5”.
故选:A.
【点评】本题考查了正方体对面的数字,判断出“邻面”“对面”是正确解答的关键.
二.填空题(共5小题)
6.(2024秋 成都期中)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,则x﹣y+z= ﹣18 .
【考点】专题:正方体相对两个面上的文字;相反数.2024
【专题】展开与折叠;空间观念.
【答案】﹣18.
【分析】根据相对面上的两个数互为相反数,则“z”与面“4”相对,面“y”与面“﹣2”相对,“x”与面“12”相对,得出x,y,z,再代入求值即可.
【解答】解:∵“z”与面“4”相对,面“y”与面“﹣2”相对,“x”与面“12”相对,
又∵相对面上的两个数互为相反数,
∴x=﹣12,y=2,z=﹣4,
∴x﹣y+z=﹣12﹣2+(﹣4)=﹣18.
【点评】本题考查相反数,正方体的相对面上的文字,掌握正方体的相对面,有理数的加减是关键.
7.(2024秋 金水区期中)用若干大小相同的小立方块搭成一个几何体,使得从上面和从左面看到的这个几何体的形状如图所示,则搭成该几何体最多需要 10 个小立方块.
【考点】由三视图判断几何体.2024
【专题】投影与视图;空间观念.
【答案】10.
【分析】在俯视图标出小正方体的个数即可解答.
【解答】解:如图所示:
搭成该几何体最多需要小立方块:3+2+2+2+1=10(个).
故答案为:10.
【点评】本题考查了由三视图判断几何体,理解视图的定义,掌握三视图的画法及形状是正确解答的前提.
8.(2024秋 汝州市期中)如图,是一个几何体表面的展开图,则这个几何体是 三棱柱 .
【考点】几何体的展开图.2024
【专题】展开与折叠;空间观念.
【答案】三棱柱.
【分析】根据侧面为n个长方形,底边为n边形,原几何体为n棱柱,依此即可求解.
【解答】解:三棱柱的侧面由3个长方形组成,底面由2个三角形组成,故原几何体为三棱柱.
故答案为:三棱柱.
【点评】本题考查了几何体的展开图,熟记几何体展开图的形状是解题关键.
9.(2024秋 龙岗区期中)由若干个相同的小正方体搭成的一个几何体,从正面和左面看到的这个几何体的形状图如图所示,则组成这个几何体的小正方体的个数最少有 9 个.
【考点】由三视图判断几何体.2024
【专题】投影与视图;空间观念.
【答案】9.
【分析】根据主视图、左视图的形状,画出需要小正方体个数最少时的俯视图,并标注所摆放的小正方体的个数即可.
【解答】解:需要小正方体个数最少时,从上面看的图形如图所示,其中数字表示该位置所摆放小正方体的个数,
因此需要的小正方体的个数最少为3+3+3=9(个),
故答案为:9.
【点评】本题考查简单组合体的三视图,理解视图的定义,掌握简单组合体三视图的画法和形状是正确解答的关键.
10.(2024秋 坪山区期中)如图,以长方形ABCD的一边为轴,将其旋转一周得到的立体图形的表面积为 80π或48π cm2.(结果保留π)
【考点】几何体的表面积;列代数式;点、线、面、体.2024
【专题】几何图形;运算能力.
【答案】80π或48π.
【分析】根据面动成体可知得到的立体图形为圆柱;以不同的边为轴旋转一周,所得到的圆柱体的底面半径和高,根据圆柱体的表面积公式计算即可.
【解答】解:长方形绕着它的一边所在的直线旋转一周,得到的立体图形是圆柱,
绕着5cm的边为轴,旋转一周所得到的是底面半径为3cm,高为5cm的圆柱体,因此表面积为2π×3×5+π×32×2=48π(cm2),
绕着3cm的边为轴,旋转一周所得到的是底面半径为5cm,高为3cm的圆柱体,因此表面积为2π×5×3+π×52×2=80π(cm2);
故答案为:80π或48π.
【点评】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
三.解答题(共5小题)
11.(2024秋 蓝田县期中)小丽利用硬纸板制成了一个底面边长都是4cm、侧棱长是6cm的直五棱柱形笔筒(有盖).
(1)这个五棱柱有多少个面?它的侧面是什么形状?这个五棱柱一共有多少条棱?
(2)这个五棱柱所有侧面的面积之和是多少?
【考点】几何体的表面积;认识立体图形.2024
【专题】几何图形;几何直观.
【答案】(1)7,长方形,15;
(2)120cm2.
【分析】(1)根据五棱柱的构造特征即可解答;
(2)根据五棱柱的侧面都是长方形,面积为长乘宽,即可求出.
【解答】解:(1)这个五棱柱有7个面,它的侧面是长方形,这个五棱柱一共有15条棱.
(2)4×6×5=120(cm2)
答:这个五棱柱所有侧面的面积之和是120cm2.
【点评】本题考查了五棱柱的构造特征,明确五棱柱的构造特征是解答的关键.
12.(2024秋 龙岗区期中)如图所示的四个图形①,②,③,④是平面图形.本题我们探索各图形顶点、边、区域三者之间的数量关系.例如,我们规定图形①的顶点数为4(顶点为A,B,C,D),边数为5(像BC,CD为其中的两条边,但BD不能再算一条边,边与边不能重叠),区域数为2(它们是两个相互独立,不重叠的小三角形区域).
(1)数一数,每一个图形各有多少个顶点?多少条边?这些边围出了多少个区域?将结果填入下表(图形①已填好).
图形标号 顶点数V 边数E 区域数F
① 4 5 2
② 5
7
3
③
6
9 4
④ 7
12
6
(2)观察上表,推断一个平面图形的顶点数V,边数E,区域数F之间有什么关系?
(3)现已知某一个平面图形的顶点数V是2024,区域数F比顶点数V多1,请你利用(2)发现的结论,确定这个图形的边数E是多少?
【考点】认识平面图形;欧拉公式.2024
【专题】规律型;多边形与平行四边形;几何直观;运算能力.
【答案】(1)7,6,12;
(2)V+F=E+1;
(3)E=4048.
【分析】(1)根据各个图形的特征以及“顶点数”,“边数”,“区域”的意义进行解答即可;
(2)根据表格中“顶点数”,“边数”,“区域”之间的关系进行解答即可;
(3)根据(2)的结论进行计算即可.
【解答】解:(1)由题意可得,
故答案为:7,6,12;
(2)由(1)中的规律可得,
V+F=E+1;
(3)∵V=2024,区域数F比顶点数V多1,
∴F=V+1=2025,
∵V+F=E+1,
∴E=V+F﹣1=4048.
【点评】本题考查认识平面图形,理解一个平面图形的“顶点数”,“边数”,“区域”的意义是正确解答的关键.
13.(2024秋 蓝田县期中)如图2是由几个完全相同的小正方体搭成的一个几何体.请画出从不同方向看该几何体得到的平面图形.
【考点】简单组合体的三视图.2024
【专题】投影与视图;空间观念.
【答案】见解答.
【分析】根据从正面看的意义,从左面看的意义,从上面看的意义,画图即可.
【解答】解:根据题意,画图如下:
.
【点评】本题考查了从不同方向看,理解不同方向看的意义,是解题的关键.
14.(2024 城关区校级期末)如图是由棱长都为1cm的6块小正方体组成的简单几何体.
(1)请在方格中画出该几何体的三个视图.
(2)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加 2 块小正方体,
【考点】简单几何体的三视图.2024
【专题】投影与视图;空间观念.
【答案】(1)见解答;
(2)2.
【分析】(1)根据简单组合体三视图的画法画出相应的图形即可;
(2)在俯视图上相应位置备注出相应摆放的数目即可.
【解答】解:(1)该几何体的主视图、左视图和俯视图如下:
(2)在备注数字的位置加摆相应数量的小正方体,
所以最多可以添加2个,
故答案为:2.
【点评】本题考查简单组合体的三视图,理解视图的意义是正确解答的前提.
15.(2024秋 七里河区校级期中)观察如图所示的直四棱柱.
(1)它有几个面?底面与侧面分别是什么图形?
(2)若底面的周长为20cm,侧棱长为8cm,则它的侧面积为多少?
【考点】几何体的表面积;认识立体图形.2024
【专题】展开与折叠;几何直观.
【答案】(1)6个面,底面为四边形,侧面为长方形;
(2)160cm2.
【分析】(1)根据直四棱柱的特征,即可得到答案;
(2)直棱柱的侧面积=底面周长×高,由此即可计算.
【解答】解:(1)由图可知:直四棱柱有6个面,底面为四边形,侧面为长方形;
(2)20×8=160(cm2),
答:直四棱柱的侧面积是160cm2.
【点评】本题考查几何体的表面积,认识立体图形,关键是掌握棱柱的概念,直棱柱侧面积的计算公式.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
