沪科版七年级数学下册8.3.2 平方差公式课件(共16张PPT)
文档属性
| 名称 | 沪科版七年级数学下册8.3.2 平方差公式课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 539.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 15:30:37 | ||
图片预览






文档简介
(共16张PPT)
8.3.2 平方差公式
比一比:
看看谁的速度快
(1) 99X101
(2)68X72
(3)57X63
(4)102X98
(5)497X503
有没有更加简便的方法?
计算下列各题:
做一做
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
=x2 9 ;
=1 4a2 ;
=x2 16y2 ;
=y2 25z2 ;
你能说出等式两边的代数式意义吗?
=x2 32 ;
=12 (2a)2 ;
=x2 (4y)2 ;
=y2 (5z)2 .
通过观察你能得到什么规律?你可以表达出来吗?
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
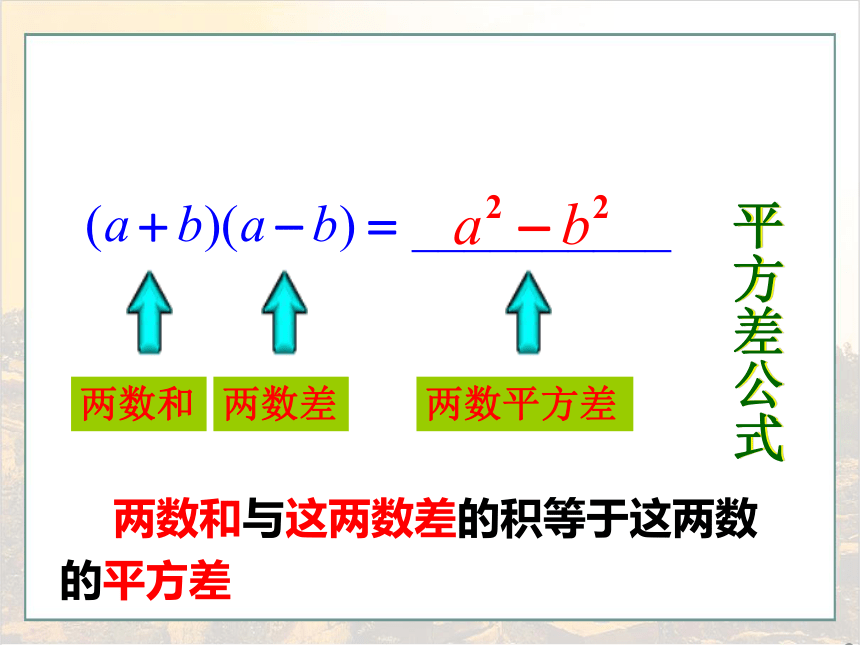
两数和
两数差
两数平方差
两数和与这两数差的积等于这两数的平方差
平方差公式
例1 利用平方差公式计算:
(5+6x)(5 6x);
(x+2y)(x 2y);
( m+n)( m n).
练习:下列式子可用平方差公式计算吗
为什么 如果能够,怎样计算
(1)(2c+3b)( 2c 3b) ;
(2)(x y)(y x) ;
(3)(d+2b)(2d+b);
(4) (a b)(a+b) ;
(5)( 2x+y)(y 2x).
(a+b)(a b)=a2 b2
(1)等号左边是两个二项式相乘.
即一项相同,一项互为相反数.
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
(3) 公式中的 a和b 可以代表数,
也可以是代数式.
注意:
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
练一练
1.计算:
(1) (x+5)(x-5)
(2) (2-3x)(3x+2)
(3) (2m+3n)(2m-3n)
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗
做一做
b
a
a
b
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
a
解决问题
比一比:
看看谁的速度快
(1) 99X101=100 -1 =9999
(2)68X72=70 -2 =4896
(3)57X63=60 -3 =3591
(4)102X98=100 -2 =9996
(5)497X503=500 -3 =249991
(1) 99X101
(2)68X72
(3)57X63
(4)102X98
(5)497X503
例2 用平方差公式计算:
运用平方差公式计算:
练习:
1、 通过本节课学习,你学到了什么
2. 你认为怎么使用平方差公式
3. 你还有什么疑惑
课后作业:
P71 习题8.3 第2题
同步练习相关部分
8.3.2 平方差公式
比一比:
看看谁的速度快
(1) 99X101
(2)68X72
(3)57X63
(4)102X98
(5)497X503
有没有更加简便的方法?
计算下列各题:
做一做
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
=x2 9 ;
=1 4a2 ;
=x2 16y2 ;
=y2 25z2 ;
你能说出等式两边的代数式意义吗?
=x2 32 ;
=12 (2a)2 ;
=x2 (4y)2 ;
=y2 (5z)2 .
通过观察你能得到什么规律?你可以表达出来吗?
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
(1) (x+3)(x 3) ;
(2) (1+2a)(1 2a) ;
(3) (x+4y)(x 4y) ;
(4) (y+5z)(y 5z) ;
两数和
两数差
两数平方差
两数和与这两数差的积等于这两数的平方差
平方差公式
例1 利用平方差公式计算:
(5+6x)(5 6x);
(x+2y)(x 2y);
( m+n)( m n).
练习:下列式子可用平方差公式计算吗
为什么 如果能够,怎样计算
(1)(2c+3b)( 2c 3b) ;
(2)(x y)(y x) ;
(3)(d+2b)(2d+b);
(4) (a b)(a+b) ;
(5)( 2x+y)(y 2x).
(a+b)(a b)=a2 b2
(1)等号左边是两个二项式相乘.
即一项相同,一项互为相反数.
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
(3) 公式中的 a和b 可以代表数,
也可以是代数式.
注意:
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
(2) 公式右边是这两个数的平方差;
相同项的平方减去相反项的平方
练一练
1.计算:
(1) (x+5)(x-5)
(2) (2-3x)(3x+2)
(3) (2m+3n)(2m-3n)
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.小明将绿色和黄色两部分拼成一个长方形.
问:小明能拼成功吗
做一做
b
a
a
b
原图实际面积为:________________
长方形的面积为:_________________
b
a
a
b
a-b
b
a
解决问题
比一比:
看看谁的速度快
(1) 99X101=100 -1 =9999
(2)68X72=70 -2 =4896
(3)57X63=60 -3 =3591
(4)102X98=100 -2 =9996
(5)497X503=500 -3 =249991
(1) 99X101
(2)68X72
(3)57X63
(4)102X98
(5)497X503
例2 用平方差公式计算:
运用平方差公式计算:
练习:
1、 通过本节课学习,你学到了什么
2. 你认为怎么使用平方差公式
3. 你还有什么疑惑
课后作业:
P71 习题8.3 第2题
同步练习相关部分
