【新课预习衔接】第十四章 全等三角形(培优卷.含解析)-2025-2026学年八年级上册数学人教版(2024)
文档属性
| 名称 | 【新课预习衔接】第十四章 全等三角形(培优卷.含解析)-2025-2026学年八年级上册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 342.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:03:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 全等三角形
一.选择题(共5小题)
1.(2024秋 江阴市期中)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数是( )
A.50° B.60° C.70° D.无法确定
2.(2024秋 越秀区校级期中)如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=16°,∠B=30°,则∠1的度数为( )
A.66° B.63° C.61° D.56°
3.(2024春 武侯区校级期中)如图,AD是△ABC的角平分线,DF⊥AB于点F,点E,G分别在AB,AC上,且DE=DG,若S△ADG=24,S△AED=18,则△DEF的面积为( )
A.3 B.4 C.5 D.6
4.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
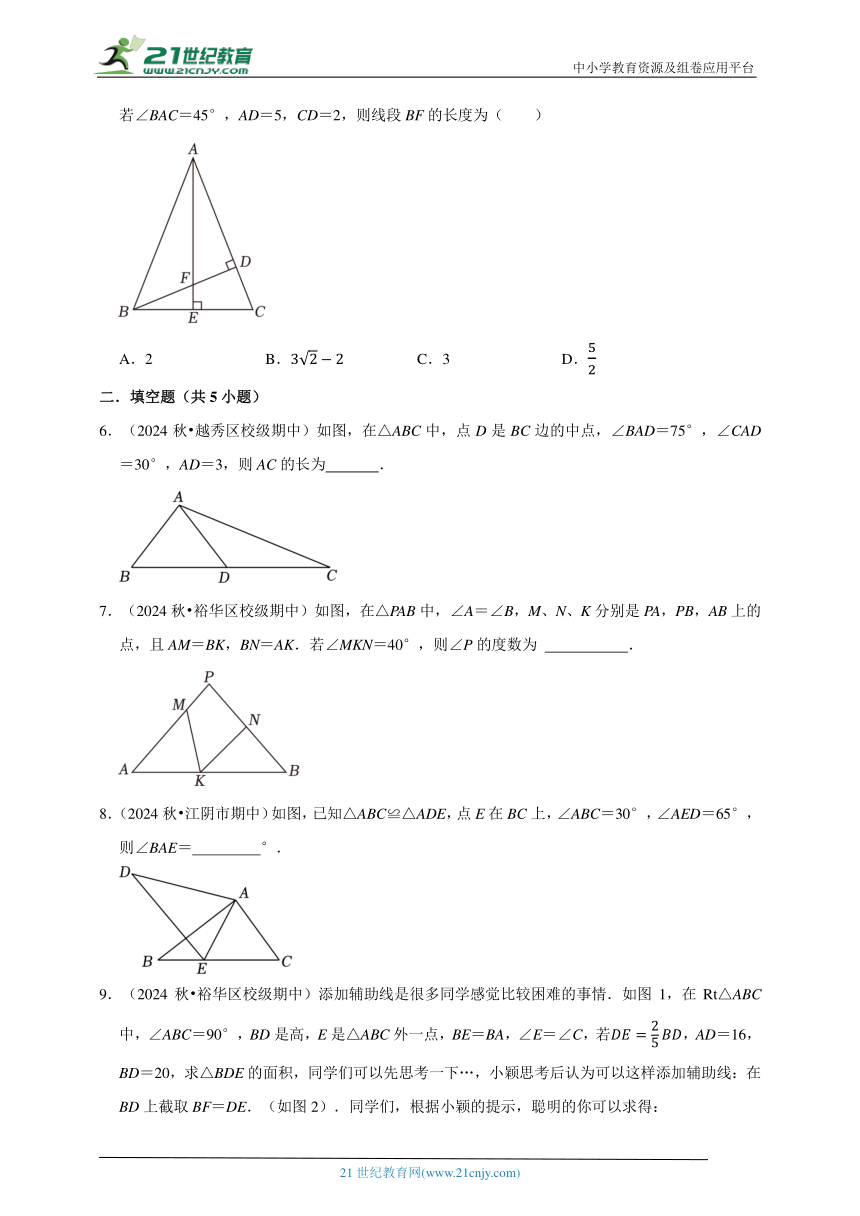
5.(2024 宁波一模)如图,在三角形ABC中,过点B,A作BD⊥AC,AE⊥BC,BD,AE交于点F,若∠BAC=45°,AD=5,CD=2,则线段BF的长度为( )
A.2 B. C.3 D.
二.填空题(共5小题)
6.(2024秋 越秀区校级期中)如图,在△ABC中,点D是BC边的中点,∠BAD=75°,∠CAD=30°,AD=3,则AC的长为 .
7.(2024秋 裕华区校级期中)如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 .
8.(2024秋 江阴市期中)如图,已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE= °.
9.(2024秋 裕华区校级期中)添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt△ABC中,∠ABC=90°,BD是高,E是△ABC外一点,BE=BA,∠E=∠C,若,AD=16,BD=20,求△BDE的面积,同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在BD上截取BF=DE.(如图2).同学们,根据小颖的提示,聪明的你可以求得:
(1)△BDE≌ ;
(2)△BDE的面积为 .
10.(2024秋 广安期末)如图,AB=8cm,∠A=∠B,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以x cm/s的速度由点B向点D运动.它们运动的时间为t(s).当△ACP与△BPQ全等时,x的值为 .
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,点B,E,C,F在同一条直线上,AB∥DE,BE=CF,∠ACB=∠F,求证:△ABC≌△DEF.
12.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
13.(2024秋 越秀区校级期中)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.求证:CF=AD.
14.(2024秋 曾都区期中)如图,在△ABC中,AB=AC,D是BC边上一点,以AD为边在AD右侧作△ADE,使AE=AD,连接CE,∠BAC=∠DAE=108°.
(1)求证:△BAD≌△CAE;
(2)若DE=DC,求∠CDE的度数.
15.(2024秋 松阳县期末)已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,连结BE交点AD于点F,BF=AC,DF=DC.
(1)求证:△BDF≌△ACD.
(2)求证:BE⊥AC.
(3)若BD=4,CD=3,求BE的长.
新课预习衔接 全等三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 江阴市期中)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数是( )
A.50° B.60° C.70° D.无法确定
【考点】全等三角形的性质;三角形内角和定理.
【专题】三角形;图形的全等;推理能力.
【答案】A
【分析】由全等三角形的对应角相等,即可得到答案.
【解答】解:∵两个三角形全等,
∴∠α=180°﹣70°﹣60°=50°.
故选:A.
【点评】本题考查全等三角形的性质,三角形内角和定理,关键是掌握全等三角形的对应角相等.
2.(2024秋 越秀区校级期中)如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=16°,∠B=30°,则∠1的度数为( )
A.66° B.63° C.61° D.56°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】先根据全等三角形的性质得到∠B=∠D=30°,∠ACB=∠AED=105°,再利用三角形外角性质计算出∠CFA=89°,则根据对顶角相等得到∠DFG=89°,然后根据三角形内角和定理计算∠1的度数即可.
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=30°,∠ACB=∠AED=105°,
∵∠ACB=∠CAD+∠CFA,
∴∠CFA=105°﹣16°=89°,
∴∠DFG=∠CFA=89°,
∵∠1+∠D+∠DFG=180°,
∴∠1=180°﹣∠D﹣∠DFG=180°﹣30°﹣89°=61°.
故选:C.
【点评】本题考查了全等三角形的性质.熟练掌握全等三角形的性质是解题的关键.
3.(2024春 武侯区校级期中)如图,AD是△ABC的角平分线,DF⊥AB于点F,点E,G分别在AB,AC上,且DE=DG,若S△ADG=24,S△AED=18,则△DEF的面积为( )
A.3 B.4 C.5 D.6
【考点】全等三角形的判定与性质;角平分线的性质.
【专题】线段、角、相交线与平行线;图形的全等;推理能力.
【答案】A
【分析】过点D作DH⊥AC于H,根据角平分线的性质得到DH=DF,进而证明Rt△DEF≌Rt△DGH,根据全等三角形的性质得到△DEF的面积=△DGH的面积,根据题意列出方程,解方程得到答案.
【解答】解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△DEF=S△DGH,
设S△DEF=S△DGH=S,
在Rt△ADF和Rt△ADH中,
,
同理可证,Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH,
∵S△ADG=24,S△AED=18,
∴24﹣S=18+S,
解得,S=3,
故选:A.
【点评】本题考查的是全等三角形的判定与性质、角平分线的性质,作辅助线构造出全等三角形并利用角平分线的性质是解题的关键.
4.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据角平分线的性质得到DE=DF,再根据三角形面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,
∴DE=DF,
∵△ABC的面积是30,AB=13,AC=7,
∴AB DEAC DF=30,即13 DE7 DE=30,
解得:DE=3,
故选:A.
【点评】本题考查的是角平分线的性质,角的平分线上的点到角的两边的距离相等.
5.(2024 宁波一模)如图,在三角形ABC中,过点B,A作BD⊥AC,AE⊥BC,BD,AE交于点F,若∠BAC=45°,AD=5,CD=2,则线段BF的长度为( )
A.2 B. C.3 D.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据ASA证明△ADF与△BDC全等,进而利用全等三角形的性质解答即可.
【解答】解:∵BD⊥AC,AE⊥BC,
∴∠BDA=∠AEC=90°,
∵∠BAC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠FAD+∠AFD=90°,∠DBC+∠BFE=90°,∠AFD=∠BFE,
∴∠FAD=∠DBC,
在△ADF与△BDC中,
,
∴△ADF≌△BDC(ASA),
∴DF=CD,
∴BF=BD﹣DF=AD﹣CD=5﹣2=3,
故选:C.
【点评】本题考查了全等三角形的判定与性质,根据ASA证明△ADF与△BDC全等解答是解题的关键.
二.填空题(共5小题)
6.(2024秋 越秀区校级期中)如图,在△ABC中,点D是BC边的中点,∠BAD=75°,∠CAD=30°,AD=3,则AC的长为 6 .
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力.
【答案】6.
【分析】作CE∥AB,交AD的延长线于E,根据等腰三角形的判定,可得AE=AC,再证明△ADB≌△EDC,即可解决问题.
【解答】解:作CE∥AB,交AD的延长线于E,如图,.
∴∠BAD=∠E=75°,
∵∠CAD=30°,
∴∠ACE=180°﹣∠E﹣∠CAE=180°﹣75°﹣30°=75°,
∴∠ACE=∠E,
∴AE=AC,
在△ADB和△EDC中,
,
∴△ADB≌△EDC(AAS),
∴ED=AD,
∴AE=2AD=6,
∴AC=AE=6.
故答案为:6.
【点评】本题考查了全等三角形的判定和性质,等角对等边,掌握其性质定理是解决此题的关键.
7.(2024秋 裕华区校级期中)如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 100° .
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力;推理能力.
【答案】100°.
【分析】证明△MAK≌△KBN,根据全等三角形的性质得到∠BKN=∠AMK,根据三角形的外角性质求出∠A,根据三角形内角和定理计算,得到答案.
【解答】解:在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠BKN=∠AMK,
∵∠MKB是△AMK的外角,
∴∠BKN+∠MKN=∠A+∠AMK,
∴∠A=∠MKN=40°,
∴∠B=∠A=40°,
∴∠P=180°﹣40°﹣40°=100°,
故答案为:100°.
【点评】本题考查的是全等三角形的判定和性质、三角形的外角性质、三角形内角和定理,掌握全等三角形的判定定理是解题的关键.
8.(2024秋 江阴市期中)如图,已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE= 35 °.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】根据全等三角形的性质求出∠C,根据三角形的外角性质计算,得到答案.
【解答】解:∵△ABC≌△ADE,
∴AE=AC,∠C=∠AED=65°,
∴∠AEC=∠C=65°,
∴∠AEC﹣∠ABC=35°,
故答案为:35.
【点评】本题考查的是全等三角形的性质、三角形的外角性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.
9.(2024秋 裕华区校级期中)添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt△ABC中,∠ABC=90°,BD是高,E是△ABC外一点,BE=BA,∠E=∠C,若,AD=16,BD=20,求△BDE的面积,同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在BD上截取BF=DE.(如图2).同学们,根据小颖的提示,聪明的你可以求得:
(1)△BDE≌ △AFB ;
(2)△BDE的面积为 64 .
【考点】全等三角形的判定与性质.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)△AFB;
(2)64.
【分析】(1)由SAS推导出△BDE≌△AFB即可;
(2)由△BDE≌△AFB求出BF,DF的长,再由面积公式求得即可.
【解答】解:(1)如图所示,连接AF,
∠ABD=180°﹣∠BDA﹣∠BAD=90°﹣∠BAD,
∠C=180°﹣∠ABC﹣∠BAD=90°﹣∠BAD,
∵∠ABD=∠C,
∵∠E=∠C,
∵∠ABD=∠E,
在△BDE与△AFB中,
,
∴△BDE≌△AFB(SAS),
故答案为:△AFB;
∴S△ABF=S△BDE,
∵,
∵BF20=8,
∴DF=BD﹣BF=20﹣8=12,
∴S△AFDAD DF12×16=96,
∵S△ABF=S△ABD﹣S△AFD,
∴S△BDE=S△ABF=160﹣96=64.
故答案为:64.
【点评】本题考查了全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.
10.(2024秋 广安期末)如图,AB=8cm,∠A=∠B,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以x cm/s的速度由点B向点D运动.它们运动的时间为t(s).当△ACP与△BPQ全等时,x的值为 1或 .
【考点】全等三角形的判定.
【专题】图形的全等;运算能力.
【答案】1或.
【分析】由题意知当△ACP与△BPQ全等,分△ACP≌△BPQ和△APC≌△BPQ两种情况,根据全等的性质列方程求解即可.
【解答】解:由题意知,AP=t,BP=8﹣t,BQ=xt,
△ACP与△BPQ全等,∠A=∠B,
∴分两种情况求解:
①当△ACP≌△BPQ时,AP=BQ,即t=xt,解得x=1;
②当△APC≌△BPQ时,AP=BP,即t=8﹣t,解得t=4,AC=BQ,即6=xt,解得;
综上所述,x的值是1或,
故答案为:1或.
【点评】本题考查了全等三角形的性质,一元一次方程的应用.解题的关键在于分情况求解.
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,点B,E,C,F在同一条直线上,AB∥DE,BE=CF,∠ACB=∠F,求证:△ABC≌△DEF.
【考点】全等三角形的判定.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先根据AB∥DE得∠B=∠DEF,再根据BE=CF得BC=EF,进而可依据“ASA”判定△△ABC和△DEF全等.
【解答】证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+CE=CF+EC.
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
【点评】此题主要考查了全等三角形的判定,平行线的性质,熟练掌握全等三角形的判定,平行线的性质是解决问题的关键.
12.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先证明△DEB和△DCF全等得DE=DC,再根据角平分线的性质即可得出结论.
【解答】证明:∵FE⊥AB,∠ACB=90°,
∴∠DEB=∠DCF=90°,
在△DEB和△DCF中,
,
∴△DEB≌△DCF(AAS),
∴DE=DC,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC.
【点评】此题主要考查了角平分线的性质,全等三角形的判定与性质,理解角平分线的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
13.(2024秋 越秀区校级期中)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.求证:CF=AD.
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】利用角角边定理判定△ADE≌△CFE(AAS)即可;利用全等三角形对应边相等可得CF=AD.
【解答】证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴CF=AD.
【点评】本题主要考查了全等三角形的判定与性质,解答本题的关键是熟练掌握全等三角形的判定定理.
14.(2024秋 曾都区期中)如图,在△ABC中,AB=AC,D是BC边上一点,以AD为边在AD右侧作△ADE,使AE=AD,连接CE,∠BAC=∠DAE=108°.
(1)求证:△BAD≌△CAE;
(2)若DE=DC,求∠CDE的度数.
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力.
【答案】(1)见解析;
(2)36°.
【分析】(1)根据SAS证明三角形全等即可.
(2)证明∠B=∠ACB=∠ACE=36°,推出∠DCE=72°,利用等腰三角形的性质以及三角形内角和定理解决问题即可.
【解答】(1)证明:∵∠BAC=∠DAE=108°,∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:∵AB=AC,∠BAC=108°,
∴∠B=∠ACB=36°,
∵△BAD≌△CAE,
∴∠B=∠ACE=36°,
∴∠DCE=∠BCA+∠ACE=36°+36°=72°,
∵DE=DC,
∴∠DEC=∠DCE=72°,
∴∠EDC=180°﹣72°﹣72°=36°,
答:∠CDE的度数为36°.
【点评】本题考查全等三角形的判定和性质,等腰三角形的性质,三角形内角和定理等知识,掌握其性质定理是解决此题的关键.
15.(2024秋 松阳县期末)已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,连结BE交点AD于点F,BF=AC,DF=DC.
(1)求证:△BDF≌△ACD.
(2)求证:BE⊥AC.
(3)若BD=4,CD=3,求BE的长.
【考点】全等三角形的判定与性质.
【专题】推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)利用HL证明Rt△ADC≌△Rt△BDF,即可;
(2)利用Rt△ADC≌Rt△BDF,得∠C=∠BFD,从而证得∠C+∠DBF=90°,即可得出结论;
(3)利用Rt△ADC≌Rt△BDF得AD=BD=4,从而求得BC=BD+CD=7,利用勾股定理求得,再利用等积法求解即可.
【解答】(1)证明:∵AD⊥BC,
∴∠ADC=∠BDF=90°,
在Rt△ADC和Rt△BDF中,
,
∴Rt△ADC≌△Rt△BDF(HL).
(2)证明:∵Rt△ADC≌Rt△BDF,
∴∠C=∠BFD,
∵∠DBF+∠BFD=90°,
∴∠C+∠DBF=90°,
∴BE⊥AC.
(3)解:∵Rt△ADC≌△Rt△BDF,
∴AD=BD=4,
∵CD=3,BD=4,
∴BC=BD+CD=7,,
∵
∴,
∴.
【点评】本题考查全等三角形的判定与性质,掌握三角形的面积,勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 全等三角形
一.选择题(共5小题)
1.(2024秋 江阴市期中)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数是( )
A.50° B.60° C.70° D.无法确定
2.(2024秋 越秀区校级期中)如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=16°,∠B=30°,则∠1的度数为( )
A.66° B.63° C.61° D.56°
3.(2024春 武侯区校级期中)如图,AD是△ABC的角平分线,DF⊥AB于点F,点E,G分别在AB,AC上,且DE=DG,若S△ADG=24,S△AED=18,则△DEF的面积为( )
A.3 B.4 C.5 D.6
4.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
5.(2024 宁波一模)如图,在三角形ABC中,过点B,A作BD⊥AC,AE⊥BC,BD,AE交于点F,若∠BAC=45°,AD=5,CD=2,则线段BF的长度为( )
A.2 B. C.3 D.
二.填空题(共5小题)
6.(2024秋 越秀区校级期中)如图,在△ABC中,点D是BC边的中点,∠BAD=75°,∠CAD=30°,AD=3,则AC的长为 .
7.(2024秋 裕华区校级期中)如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 .
8.(2024秋 江阴市期中)如图,已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE= °.
9.(2024秋 裕华区校级期中)添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt△ABC中,∠ABC=90°,BD是高,E是△ABC外一点,BE=BA,∠E=∠C,若,AD=16,BD=20,求△BDE的面积,同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在BD上截取BF=DE.(如图2).同学们,根据小颖的提示,聪明的你可以求得:
(1)△BDE≌ ;
(2)△BDE的面积为 .
10.(2024秋 广安期末)如图,AB=8cm,∠A=∠B,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以x cm/s的速度由点B向点D运动.它们运动的时间为t(s).当△ACP与△BPQ全等时,x的值为 .
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,点B,E,C,F在同一条直线上,AB∥DE,BE=CF,∠ACB=∠F,求证:△ABC≌△DEF.
12.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
13.(2024秋 越秀区校级期中)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.求证:CF=AD.
14.(2024秋 曾都区期中)如图,在△ABC中,AB=AC,D是BC边上一点,以AD为边在AD右侧作△ADE,使AE=AD,连接CE,∠BAC=∠DAE=108°.
(1)求证:△BAD≌△CAE;
(2)若DE=DC,求∠CDE的度数.
15.(2024秋 松阳县期末)已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,连结BE交点AD于点F,BF=AC,DF=DC.
(1)求证:△BDF≌△ACD.
(2)求证:BE⊥AC.
(3)若BD=4,CD=3,求BE的长.
新课预习衔接 全等三角形
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 江阴市期中)如图是两个全等三角形,图中字母表示三角形的边长,则∠α的度数是( )
A.50° B.60° C.70° D.无法确定
【考点】全等三角形的性质;三角形内角和定理.
【专题】三角形;图形的全等;推理能力.
【答案】A
【分析】由全等三角形的对应角相等,即可得到答案.
【解答】解:∵两个三角形全等,
∴∠α=180°﹣70°﹣60°=50°.
故选:A.
【点评】本题考查全等三角形的性质,三角形内角和定理,关键是掌握全等三角形的对应角相等.
2.(2024秋 越秀区校级期中)如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G.若∠AED=105°,∠CAD=16°,∠B=30°,则∠1的度数为( )
A.66° B.63° C.61° D.56°
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】先根据全等三角形的性质得到∠B=∠D=30°,∠ACB=∠AED=105°,再利用三角形外角性质计算出∠CFA=89°,则根据对顶角相等得到∠DFG=89°,然后根据三角形内角和定理计算∠1的度数即可.
【解答】解:∵△ABC≌△ADE,
∴∠B=∠D=30°,∠ACB=∠AED=105°,
∵∠ACB=∠CAD+∠CFA,
∴∠CFA=105°﹣16°=89°,
∴∠DFG=∠CFA=89°,
∵∠1+∠D+∠DFG=180°,
∴∠1=180°﹣∠D﹣∠DFG=180°﹣30°﹣89°=61°.
故选:C.
【点评】本题考查了全等三角形的性质.熟练掌握全等三角形的性质是解题的关键.
3.(2024春 武侯区校级期中)如图,AD是△ABC的角平分线,DF⊥AB于点F,点E,G分别在AB,AC上,且DE=DG,若S△ADG=24,S△AED=18,则△DEF的面积为( )
A.3 B.4 C.5 D.6
【考点】全等三角形的判定与性质;角平分线的性质.
【专题】线段、角、相交线与平行线;图形的全等;推理能力.
【答案】A
【分析】过点D作DH⊥AC于H,根据角平分线的性质得到DH=DF,进而证明Rt△DEF≌Rt△DGH,根据全等三角形的性质得到△DEF的面积=△DGH的面积,根据题意列出方程,解方程得到答案.
【解答】解:过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DH=DF,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△DEF=S△DGH,
设S△DEF=S△DGH=S,
在Rt△ADF和Rt△ADH中,
,
同理可证,Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH,
∵S△ADG=24,S△AED=18,
∴24﹣S=18+S,
解得,S=3,
故选:A.
【点评】本题考查的是全等三角形的判定与性质、角平分线的性质,作辅助线构造出全等三角形并利用角平分线的性质是解题的关键.
4.(2024秋 广州期中)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,△ABC的面积是30,AB=13,AC=7,则DE的长( )
A.3 B.4 C.5 D.6
【考点】角平分线的性质.
【专题】三角形;推理能力.
【答案】A
【分析】根据角平分线的性质得到DE=DF,再根据三角形面积公式计算即可.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB于B,DF⊥AC于F,
∴DE=DF,
∵△ABC的面积是30,AB=13,AC=7,
∴AB DEAC DF=30,即13 DE7 DE=30,
解得:DE=3,
故选:A.
【点评】本题考查的是角平分线的性质,角的平分线上的点到角的两边的距离相等.
5.(2024 宁波一模)如图,在三角形ABC中,过点B,A作BD⊥AC,AE⊥BC,BD,AE交于点F,若∠BAC=45°,AD=5,CD=2,则线段BF的长度为( )
A.2 B. C.3 D.
【考点】全等三角形的判定与性质.
【专题】图形的全等;推理能力.
【答案】C
【分析】根据ASA证明△ADF与△BDC全等,进而利用全等三角形的性质解答即可.
【解答】解:∵BD⊥AC,AE⊥BC,
∴∠BDA=∠AEC=90°,
∵∠BAC=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵∠FAD+∠AFD=90°,∠DBC+∠BFE=90°,∠AFD=∠BFE,
∴∠FAD=∠DBC,
在△ADF与△BDC中,
,
∴△ADF≌△BDC(ASA),
∴DF=CD,
∴BF=BD﹣DF=AD﹣CD=5﹣2=3,
故选:C.
【点评】本题考查了全等三角形的判定与性质,根据ASA证明△ADF与△BDC全等解答是解题的关键.
二.填空题(共5小题)
6.(2024秋 越秀区校级期中)如图,在△ABC中,点D是BC边的中点,∠BAD=75°,∠CAD=30°,AD=3,则AC的长为 6 .
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力.
【答案】6.
【分析】作CE∥AB,交AD的延长线于E,根据等腰三角形的判定,可得AE=AC,再证明△ADB≌△EDC,即可解决问题.
【解答】解:作CE∥AB,交AD的延长线于E,如图,.
∴∠BAD=∠E=75°,
∵∠CAD=30°,
∴∠ACE=180°﹣∠E﹣∠CAE=180°﹣75°﹣30°=75°,
∴∠ACE=∠E,
∴AE=AC,
在△ADB和△EDC中,
,
∴△ADB≌△EDC(AAS),
∴ED=AD,
∴AE=2AD=6,
∴AC=AE=6.
故答案为:6.
【点评】本题考查了全等三角形的判定和性质,等角对等边,掌握其性质定理是解决此题的关键.
7.(2024秋 裕华区校级期中)如图,在△PAB中,∠A=∠B,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 100° .
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力;推理能力.
【答案】100°.
【分析】证明△MAK≌△KBN,根据全等三角形的性质得到∠BKN=∠AMK,根据三角形的外角性质求出∠A,根据三角形内角和定理计算,得到答案.
【解答】解:在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠BKN=∠AMK,
∵∠MKB是△AMK的外角,
∴∠BKN+∠MKN=∠A+∠AMK,
∴∠A=∠MKN=40°,
∴∠B=∠A=40°,
∴∠P=180°﹣40°﹣40°=100°,
故答案为:100°.
【点评】本题考查的是全等三角形的判定和性质、三角形的外角性质、三角形内角和定理,掌握全等三角形的判定定理是解题的关键.
8.(2024秋 江阴市期中)如图,已知△ABC≌△ADE,点E在BC上,∠ABC=30°,∠AED=65°,则∠BAE= 35 °.
【考点】全等三角形的性质.
【专题】图形的全等;推理能力.
【答案】见试题解答内容
【分析】根据全等三角形的性质求出∠C,根据三角形的外角性质计算,得到答案.
【解答】解:∵△ABC≌△ADE,
∴AE=AC,∠C=∠AED=65°,
∴∠AEC=∠C=65°,
∴∠AEC﹣∠ABC=35°,
故答案为:35.
【点评】本题考查的是全等三角形的性质、三角形的外角性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.
9.(2024秋 裕华区校级期中)添加辅助线是很多同学感觉比较困难的事情.如图1,在Rt△ABC中,∠ABC=90°,BD是高,E是△ABC外一点,BE=BA,∠E=∠C,若,AD=16,BD=20,求△BDE的面积,同学们可以先思考一下…,小颖思考后认为可以这样添加辅助线:在BD上截取BF=DE.(如图2).同学们,根据小颖的提示,聪明的你可以求得:
(1)△BDE≌ △AFB ;
(2)△BDE的面积为 64 .
【考点】全等三角形的判定与性质.
【专题】图形的全等;等腰三角形与直角三角形;推理能力.
【答案】(1)△AFB;
(2)64.
【分析】(1)由SAS推导出△BDE≌△AFB即可;
(2)由△BDE≌△AFB求出BF,DF的长,再由面积公式求得即可.
【解答】解:(1)如图所示,连接AF,
∠ABD=180°﹣∠BDA﹣∠BAD=90°﹣∠BAD,
∠C=180°﹣∠ABC﹣∠BAD=90°﹣∠BAD,
∵∠ABD=∠C,
∵∠E=∠C,
∵∠ABD=∠E,
在△BDE与△AFB中,
,
∴△BDE≌△AFB(SAS),
故答案为:△AFB;
∴S△ABF=S△BDE,
∵,
∵BF20=8,
∴DF=BD﹣BF=20﹣8=12,
∴S△AFDAD DF12×16=96,
∵S△ABF=S△ABD﹣S△AFD,
∴S△BDE=S△ABF=160﹣96=64.
故答案为:64.
【点评】本题考查了全等三角形的判定与性质,掌握全等三角形的判定与性质是解题的关键.
10.(2024秋 广安期末)如图,AB=8cm,∠A=∠B,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以x cm/s的速度由点B向点D运动.它们运动的时间为t(s).当△ACP与△BPQ全等时,x的值为 1或 .
【考点】全等三角形的判定.
【专题】图形的全等;运算能力.
【答案】1或.
【分析】由题意知当△ACP与△BPQ全等,分△ACP≌△BPQ和△APC≌△BPQ两种情况,根据全等的性质列方程求解即可.
【解答】解:由题意知,AP=t,BP=8﹣t,BQ=xt,
△ACP与△BPQ全等,∠A=∠B,
∴分两种情况求解:
①当△ACP≌△BPQ时,AP=BQ,即t=xt,解得x=1;
②当△APC≌△BPQ时,AP=BP,即t=8﹣t,解得t=4,AC=BQ,即6=xt,解得;
综上所述,x的值是1或,
故答案为:1或.
【点评】本题考查了全等三角形的性质,一元一次方程的应用.解题的关键在于分情况求解.
三.解答题(共5小题)
11.(2024秋 大足区期中)如图,点B,E,C,F在同一条直线上,AB∥DE,BE=CF,∠ACB=∠F,求证:△ABC≌△DEF.
【考点】全等三角形的判定.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先根据AB∥DE得∠B=∠DEF,再根据BE=CF得BC=EF,进而可依据“ASA”判定△△ABC和△DEF全等.
【解答】证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=CF,
∴BE+CE=CF+EC.
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
【点评】此题主要考查了全等三角形的判定,平行线的性质,熟练掌握全等三角形的判定,平行线的性质是解决问题的关键.
12.(2024秋 大足区期中)如图,在△ABC中,∠ACB=90°,延长AC至点F,过点F作AB的垂线交BC于点D,交AB于点E,BE=CF,连接AD,求证:AD平分∠BAC.
【考点】角平分线的性质;全等三角形的判定与性质.
【专题】三角形;图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】先证明△DEB和△DCF全等得DE=DC,再根据角平分线的性质即可得出结论.
【解答】证明:∵FE⊥AB,∠ACB=90°,
∴∠DEB=∠DCF=90°,
在△DEB和△DCF中,
,
∴△DEB≌△DCF(AAS),
∴DE=DC,
∴点D在∠BAC的平分线上,
∴AD平分∠BAC.
【点评】此题主要考查了角平分线的性质,全等三角形的判定与性质,理解角平分线的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
13.(2024秋 越秀区校级期中)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于点E,DE=EF.求证:CF=AD.
【考点】全等三角形的判定与性质.
【专题】图形的全等;几何直观;推理能力.
【答案】证明见解答过程.
【分析】利用角角边定理判定△ADE≌△CFE(AAS)即可;利用全等三角形对应边相等可得CF=AD.
【解答】证明:∵CF∥AB,
∴∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴CF=AD.
【点评】本题主要考查了全等三角形的判定与性质,解答本题的关键是熟练掌握全等三角形的判定定理.
14.(2024秋 曾都区期中)如图,在△ABC中,AB=AC,D是BC边上一点,以AD为边在AD右侧作△ADE,使AE=AD,连接CE,∠BAC=∠DAE=108°.
(1)求证:△BAD≌△CAE;
(2)若DE=DC,求∠CDE的度数.
【考点】全等三角形的判定与性质.
【专题】图形的全等;运算能力.
【答案】(1)见解析;
(2)36°.
【分析】(1)根据SAS证明三角形全等即可.
(2)证明∠B=∠ACB=∠ACE=36°,推出∠DCE=72°,利用等腰三角形的性质以及三角形内角和定理解决问题即可.
【解答】(1)证明:∵∠BAC=∠DAE=108°,∠BAC=∠BAD+∠DAC,∠DAE=∠DAC+∠CAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:∵AB=AC,∠BAC=108°,
∴∠B=∠ACB=36°,
∵△BAD≌△CAE,
∴∠B=∠ACE=36°,
∴∠DCE=∠BCA+∠ACE=36°+36°=72°,
∵DE=DC,
∴∠DEC=∠DCE=72°,
∴∠EDC=180°﹣72°﹣72°=36°,
答:∠CDE的度数为36°.
【点评】本题考查全等三角形的判定和性质,等腰三角形的性质,三角形内角和定理等知识,掌握其性质定理是解决此题的关键.
15.(2024秋 松阳县期末)已知:如图,在△ABC中,AD⊥BC于点D,E是AC上一点,连结BE交点AD于点F,BF=AC,DF=DC.
(1)求证:△BDF≌△ACD.
(2)求证:BE⊥AC.
(3)若BD=4,CD=3,求BE的长.
【考点】全等三角形的判定与性质.
【专题】推理能力.
【答案】(1)见解析;
(2)见解析;
(3).
【分析】(1)利用HL证明Rt△ADC≌△Rt△BDF,即可;
(2)利用Rt△ADC≌Rt△BDF,得∠C=∠BFD,从而证得∠C+∠DBF=90°,即可得出结论;
(3)利用Rt△ADC≌Rt△BDF得AD=BD=4,从而求得BC=BD+CD=7,利用勾股定理求得,再利用等积法求解即可.
【解答】(1)证明:∵AD⊥BC,
∴∠ADC=∠BDF=90°,
在Rt△ADC和Rt△BDF中,
,
∴Rt△ADC≌△Rt△BDF(HL).
(2)证明:∵Rt△ADC≌Rt△BDF,
∴∠C=∠BFD,
∵∠DBF+∠BFD=90°,
∴∠C+∠DBF=90°,
∴BE⊥AC.
(3)解:∵Rt△ADC≌△Rt△BDF,
∴AD=BD=4,
∵CD=3,BD=4,
∴BC=BD+CD=7,,
∵
∴,
∴.
【点评】本题考查全等三角形的判定与性质,掌握三角形的面积,勾股定理是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
