【新课预习衔接】15.2画轴对称图形(培优卷.含解析)-2025-2026学年八年级上册数学人教版(2024)
文档属性
| 名称 | 【新课预习衔接】15.2画轴对称图形(培优卷.含解析)-2025-2026学年八年级上册数学人教版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:01:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 画轴对称图形
一.选择题(共6小题)
1.(2024秋 蓝田县期中)在平面直角坐标系中,若点A(a,3)与点B(﹣2,b)关于y轴对称,则点M(b,a)所在的象限是( )
A.第二象限 B.第四象限 C.第一象限 D.第三象限
2.(2024秋 雁塔区校级期中)在平面直角坐标系中,点A(﹣2,m﹣1)与点B(n+4,3)关于x轴对称,则的值是( )
A.﹣8 B.2 C. D.﹣2
3.(2024秋 文峰区期末)如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
4.(2024秋 五华区校级期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
5.(2024秋 市南区校级期中)如图,战机在空中展示的图形是轴对称队形,以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(50,m),则飞机D的坐标为( )
A.(﹣50,m) B.(50,﹣m) C.(﹣50,﹣m) D.(m,﹣50)
6.(2024 龙岩模拟)平面直角坐标系xOy中,A(1,0),,则坐标原点O关于直线AB对称的点O′的坐标为( )
A.(2,1) B.
C. D.
二.填空题(共5小题)
7.(2024秋 闽侯县期中)在平面直角坐标系xOy中,若A(m,4),B(2,m﹣2n)两点关于x轴对称,则mn的值为 .
8.(2024秋 河西区期中)点M(1,﹣6)关于y轴对称的点的坐标为 .
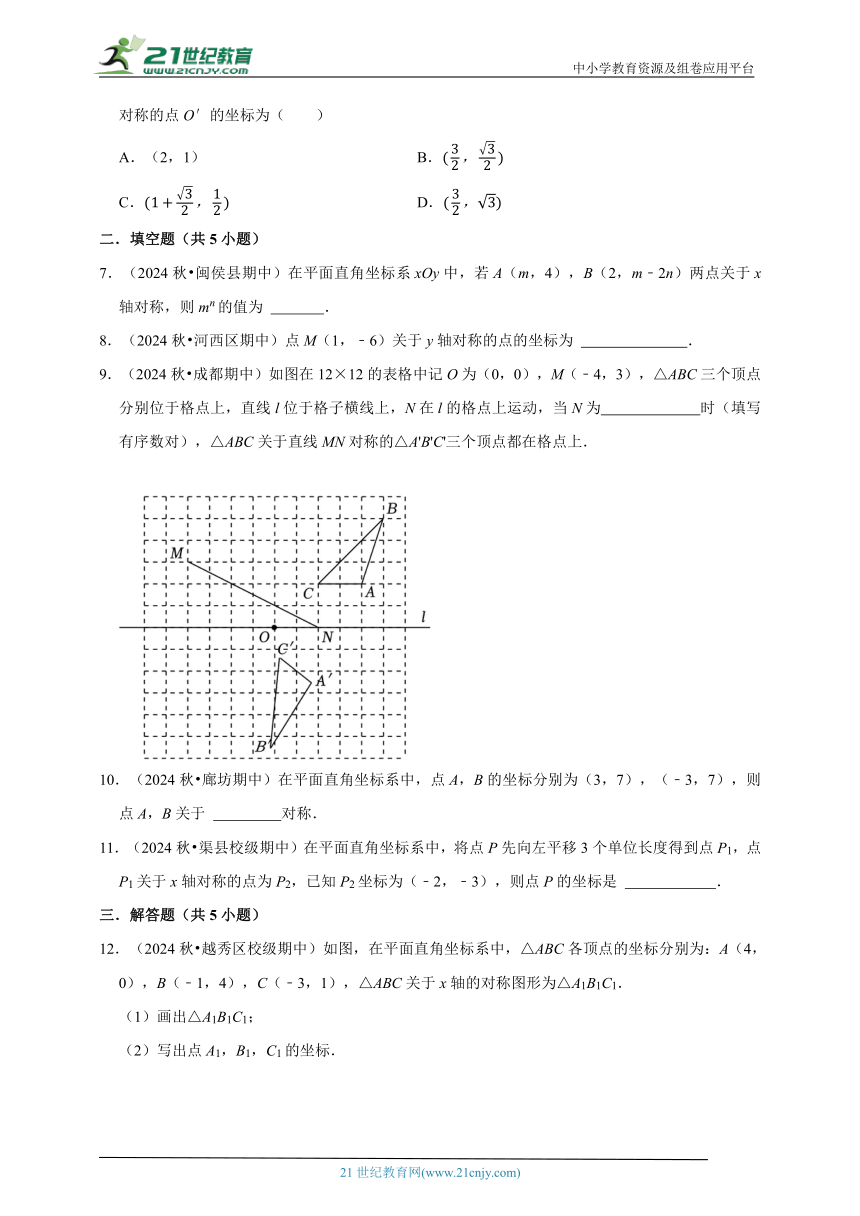
9.(2024秋 成都期中)如图在12×12的表格中记O为(0,0),M(﹣4,3),△ABC三个顶点分别位于格点上,直线l位于格子横线上,N在l的格点上运动,当N为 时(填写有序数对),△ABC关于直线MN对称的△A'B'C'三个顶点都在格点上.
10.(2024秋 廊坊期中)在平面直角坐标系中,点A,B的坐标分别为(3,7),(﹣3,7),则点A,B关于 对称.
11.(2024秋 渠县校级期中)在平面直角坐标系中,将点P先向左平移3个单位长度得到点P1,点P1关于x轴对称的点为P2,已知P2坐标为(﹣2,﹣3),则点P的坐标是 .
三.解答题(共5小题)
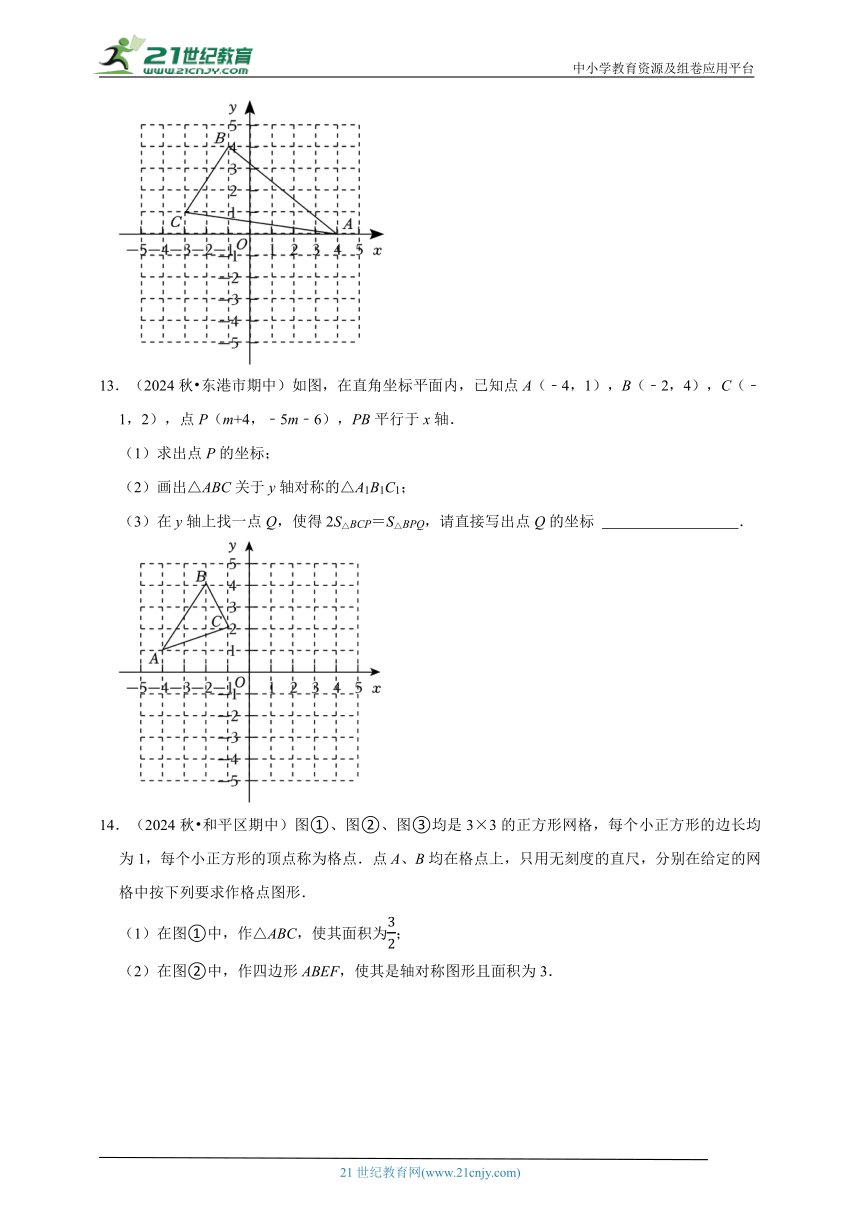
12.(2024秋 越秀区校级期中)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1),△ABC关于x轴的对称图形为△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1,B1,C1的坐标.
13.(2024秋 东港市期中)如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 .
14.(2024秋 和平区期中)图①、图②、图③均是3×3的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作格点图形.
(1)在图①中,作△ABC,使其面积为;
(2)在图②中,作四边形ABEF,使其是轴对称图形且面积为3.
15.(2024秋 恩平市期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2024的值.
16.(2024秋 南岗区校级期中)如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上,A(﹣3,3),B(﹣4,﹣2),C(0,﹣1).
(1)直接写出△ABC的面积为 ;
(2)画出△ABC关于y轴的对称的△DEC(点D与点A对应,点E与点B对应),点E的坐标为 ;
(3)用无刻度的直尺,运用所学的知识作出△ABC的高线AF(保留作图痕迹并写出理由).
新课预习衔接 画轴对称图形
参考答案与试题解析
一.选择题(共6小题)
1.(2024秋 蓝田县期中)在平面直角坐标系中,若点A(a,3)与点B(﹣2,b)关于y轴对称,则点M(b,a)所在的象限是( )
A.第二象限 B.第四象限 C.第一象限 D.第三象限
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】C
【分析】根据关于y轴对称的点的坐标特点解答即可.
【解答】解:由题意,得a=2,b=3,
故M(b,a)即M(3,2)在第一象限,
故选:C.
【点评】此题考查关于y轴对称的点的坐标,熟知关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变是解题的关键.
2.(2024秋 雁塔区校级期中)在平面直角坐标系中,点A(﹣2,m﹣1)与点B(n+4,3)关于x轴对称,则的值是( )
A.﹣8 B.2 C. D.﹣2
【考点】关于x轴、y轴对称的点的坐标;立方根.
【专题】平面直角坐标系;运算能力.
【答案】D
【分析】根据关于x轴对称点的坐标性质“横坐标相等,纵坐标互为相反数”,求解即可.
【解答】解:由题意可得:n+4=﹣2,m﹣1=﹣3,
解得n=﹣6,m=﹣2,
∴2.
故选:D.
【点评】本题考查了关于x轴、y轴对称的点的坐标,熟练掌握关于x轴、y轴对称的点的坐标的特点是解题的关键.
3.(2024秋 文峰区期末)如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系.
【答案】D
【分析】直接利用关于x轴对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.(2024秋 五华区校级期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】由点A与点B对称,求得对称轴为直线x=3,再根据点C与点D对称,即可求解.
【解答】解:∵(2,0)与(4,0)对称,
∴对称轴为直线,
∵C(0.5,4)与点D关于直线x=3对称,
∴点D的坐标为(5.5,4).
故选:B.
【点评】本题考查了轴对称的性质,熟练掌握对称点到对称轴的距离相等是解答本题的关键.
5.(2024秋 市南区校级期中)如图,战机在空中展示的图形是轴对称队形,以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(50,m),则飞机D的坐标为( )
A.(﹣50,m) B.(50,﹣m) C.(﹣50,﹣m) D.(m,﹣50)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】A
【分析】根据轴对称的性质即可得到结论.
【解答】解:∵飞机E(50,m)与飞机D关于y轴对称,
∴飞机D的坐标为(﹣50,m),
故选:A.
【点评】本题考查了坐标与图形变化﹣对称,熟练掌握轴对称的性质是解题的关键.
6.(2024 龙岩模拟)平面直角坐标系xOy中,A(1,0),,则坐标原点O关于直线AB对称的点O′的坐标为( )
A.(2,1) B.
C. D.
【考点】坐标与图形变化﹣对称.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】设直线AB的解析式为y=kx+b(k≠0),利用待定系数法求出直线AB的解析式,再由坐标原点O关于直线AB对称的点为O′,可得出直线OO′的解析式,求出直线AB与直线OO′的交点坐标,再利用中点坐标公式即可得出点O′的坐标.
【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵A(1,0),,
∴,
解得,
∴直线AB的解析式为yx,
∵坐标原点O关于直线AB对称的点为O′,
∴直线OO′的解析式为yx,
∴,
解得,
∴直线AB与直线OO′的交点坐标为(,),
设点O′(a,b),则,,
∴a,b,
∴O′(,).
故选:B.
【点评】本题考查的是坐标与图形变化﹣对称,熟知轴对称的性质是解题的关键.
二.填空题(共5小题)
7.(2024秋 闽侯县期中)在平面直角坐标系xOy中,若A(m,4),B(2,m﹣2n)两点关于x轴对称,则mn的值为 8 .
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】见试题解答内容
【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数,可得答案.
【解答】解:∵A(m,4),B(2,m﹣2n)两点关于x轴对称,
∴m=2,m﹣2n=﹣4,
解得m=2,n=3,
∴mn=23=8.
故答案为:8.
【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
8.(2024秋 河西区期中)点M(1,﹣6)关于y轴对称的点的坐标为 (﹣1,﹣6) .
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】(﹣1,﹣6).
【分析】关于y轴的对称点的坐标特点为:横坐标互为相反数,纵坐标不变,据此求解即可.
【解答】解:点M(1,﹣6)关于y轴对称的点的坐标为(﹣1,﹣6).
故答案为:(﹣1,﹣6).
【点评】本题主要考查了关于x轴、y轴对称的点的坐标,掌握平面直角坐标系中对称点的规律是解答本题的关键.
9.(2024秋 成都期中)如图在12×12的表格中记O为(0,0),M(﹣4,3),△ABC三个顶点分别位于格点上,直线l位于格子横线上,N在l的格点上运动,当N为 (﹣1,0) 时(填写有序数对),△ABC关于直线MN对称的△A'B'C'三个顶点都在格点上.
【考点】坐标与图形变化﹣对称.
【专题】平移、旋转与对称;几何直观.
【答案】(﹣1,0).
【分析】根据题意,画出点N符合条件的示意图即可解决问题.
【解答】解:由BC于AC的位置可知,
当MN与直线l的夹角为45°时,A,B,C三个点关于直线MN的对称点都在格点上.
如图所示,
所以点N为(﹣1,0).
故答案为:(﹣1,0).
【点评】本题主要考查了坐标与图形变化﹣对称,熟知图形对称的性质是解题的关键.
10.(2024秋 廊坊期中)在平面直角坐标系中,点A,B的坐标分别为(3,7),(﹣3,7),则点A,B关于 y轴 对称.
【考点】关于x轴、y轴对称的点的坐标.
【专题】平移、旋转与对称;符号意识.
【答案】y轴.
【分析】根据关于y轴对称的点的坐标特点解答即可.
【解答】解:由题意可知,点A,B 的横坐标互为相反数,纵坐标相同,
∴点 A,B 关于y轴对称.
故答案为:y轴.
【点评】本题考查了关于x,y轴对称的点的坐标,熟知关于y轴对称的点,纵坐标相同,横坐标互为相反数是解题的关键.
11.(2024秋 渠县校级期中)在平面直角坐标系中,将点P先向左平移3个单位长度得到点P1,点P1关于x轴对称的点为P2,已知P2坐标为(﹣2,﹣3),则点P的坐标是 (1,3) .
【考点】关于x轴、y轴对称的点的坐标;坐标与图形变化﹣平移.
【专题】平面直角坐标系;应用意识.
【答案】(1,3).
【分析】注意求原来点的坐标让平移的方向相反即可.根据关于x轴对称的点,横坐标不变,纵坐标变为相反数,可得出P1的坐标,再将P1向平移4个单位长度可得出P的坐标.
【解答】解:∵点P1与P2(﹣2,﹣3)关于x轴对称,
∴P1的坐标为(﹣2,3);
又∵点P先向左平移3个单位长度得到点P1,
∴点P1(﹣2,3)先向右平移3个单位长度得到点P(1,3),
故答案为:(1,3).
【点评】本题考查坐标的平移、对称,掌握平移和对称的规律是解题的关键,注意平移规律:左右平移只改变点的横坐标,左减右加;两点关于x轴对称,横坐标不变,纵坐标互为相反数.
三.解答题(共5小题)
12.(2024秋 越秀区校级期中)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1),△ABC关于x轴的对称图形为△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1,B1,C1的坐标.
【考点】作图﹣轴对称变换;坐标与图形性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)A1(4,0),B1(﹣1,﹣4),C1(﹣3,﹣1).
【分析】(1)根据关于x轴对称的点的横坐标相同,纵坐标互为相反数找到A、B、C对顶点A1、B1、C1的位置,然后顺次连接即可得出△A1B1C1,由图即可得出A1、B1、C1的坐标;
(2)根据A1、B1、C1的位置,直接写出点的坐标即可.
【解答】解:(1)如图,△A1B1C1即为所求,
(2)点A1(4,0),B1(﹣1,﹣4),C1(﹣3,﹣1).
【点评】本题考查了作图—轴对称变换、坐标与图形、割补法求三角形面积,熟练掌握轴对称的性质是解此题的关键.
13.(2024秋 东港市期中)如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 (0,0)或(0,8) .
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)P(2,4);
(2)见解析;
(3)(0,0)或(0,8).
【分析】(1)由PB平行于x轴,可得﹣5m﹣6=4,进而求得m的值即可求解;
(2)利用轴对称变换的性质作出A,B,C的对应点A1,B1,C1,再依次连接即可;
(3)设Q(0,m),根据坐标可得S△BCPPB |yC﹣yB|4×|2﹣4|=4,解得2S△BCP=S△BPQ建立方程求解即可.
【解答】解:(1)∵B(﹣2,4),点P(m+4,﹣5m﹣6),PB平行于x轴,
∴﹣5m﹣6=4,解得:m=﹣2,则m+4=2,
∴P(2,4);
(2)如图所示;
(3)∵B(﹣2,4),C(﹣1,2),P(2,4),设Q(0,n),
∴BP=4,
则S△BCPPB |yC﹣yB|4×|2﹣4|=4,
∵2S△BCP=S△BPQ,
∴S△BPQBP|yQ﹣yB|4×|n﹣4|=8,
即:|n﹣4|=4,
∴n=0或n=8,
∴点Q的坐标为(0,0)或(0,8);
故答案为:(0,0)或(0,8).
【点评】本题考查作图—轴对称变换,三角形的面积,图形与坐标,解题的关键是解题的关键是掌握相关知识的灵活运用.
14.(2024秋 和平区期中)图①、图②、图③均是3×3的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作格点图形.
(1)在图①中,作△ABC,使其面积为;
(2)在图②中,作四边形ABEF,使其是轴对称图形且面积为3.
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据题意,画底为3,高为1的三角形即可.
(2)根据轴对称图形的定义按要求画图即可.
【解答】解:(1)如图①,△ABC即为所求(答案不唯一).
(2)如图②,四边形ABEF即为所求.
【点评】本题考查作图﹣轴对称变换,熟练掌握轴对称图形的定义是解答本题的关键.
15.(2024秋 恩平市期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2024的值.
【考点】关于x轴、y轴对称的点的坐标;代数式求值.
【专题】平面直角坐标系;应用意识.
【答案】(1)a=﹣8,b=﹣5;
(2)1.
【分析】(1)根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程组求解即可;
(2)根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”列方程组求出a、b的值,然后代入代数式进行计算即可.
【解答】解:(1)∵点A、B关于x轴对称,
∴,
解得,
∴a=﹣8,b=﹣5;
(2)∵点A、B关于y轴对称,
∴,
解得,
∴(4a+b)2024=(﹣4+3)2024=1.
【点评】本题考查了关于x轴、y轴对称的点的坐标,代数式求值,解题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数.
16.(2024秋 南岗区校级期中)如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上,A(﹣3,3),B(﹣4,﹣2),C(0,﹣1).
(1)直接写出△ABC的面积为 9.5 ;
(2)画出△ABC关于y轴的对称的△DEC(点D与点A对应,点E与点B对应),点E的坐标为 (4,﹣2) ;
(3)用无刻度的直尺,运用所学的知识作出△ABC的高线AF(保留作图痕迹并写出理由).
【考点】作图﹣轴对称变换;三角形的角平分线、中线和高.
【专题】作图题;几何直观.
【答案】(1)9.5;
(2)(4,﹣2),
(3)见解析.
【分析】(1)用矩形的面积减去四周三个三角形的面积即可;
(2)分别作出点A、B关于y轴的对称点,再与点C首尾顺次连接即可;
(3)根据网格特点找到点E,连接AE交BC于一点F,于是得到结论.
【解答】解:(1)△ABC的面积为4×51×53×41×4=9.5,
故答案为:9.5;
(2)如图所示,△DEC即为所求,点E的坐标为(4,﹣2),
(3)如图所示,AF即为所求.
∵△AEH≌△CGB(SSS),
∴∠BCG=∠ECH,
∵∠AEH=∠CEF,
∴∠AHE=∠CFE=90°,
∴AF⊥BC.
【点评】本题主要考查作图—轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 画轴对称图形
一.选择题(共6小题)
1.(2024秋 蓝田县期中)在平面直角坐标系中,若点A(a,3)与点B(﹣2,b)关于y轴对称,则点M(b,a)所在的象限是( )
A.第二象限 B.第四象限 C.第一象限 D.第三象限
2.(2024秋 雁塔区校级期中)在平面直角坐标系中,点A(﹣2,m﹣1)与点B(n+4,3)关于x轴对称,则的值是( )
A.﹣8 B.2 C. D.﹣2
3.(2024秋 文峰区期末)如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
4.(2024秋 五华区校级期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
5.(2024秋 市南区校级期中)如图,战机在空中展示的图形是轴对称队形,以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(50,m),则飞机D的坐标为( )
A.(﹣50,m) B.(50,﹣m) C.(﹣50,﹣m) D.(m,﹣50)
6.(2024 龙岩模拟)平面直角坐标系xOy中,A(1,0),,则坐标原点O关于直线AB对称的点O′的坐标为( )
A.(2,1) B.
C. D.
二.填空题(共5小题)
7.(2024秋 闽侯县期中)在平面直角坐标系xOy中,若A(m,4),B(2,m﹣2n)两点关于x轴对称,则mn的值为 .
8.(2024秋 河西区期中)点M(1,﹣6)关于y轴对称的点的坐标为 .
9.(2024秋 成都期中)如图在12×12的表格中记O为(0,0),M(﹣4,3),△ABC三个顶点分别位于格点上,直线l位于格子横线上,N在l的格点上运动,当N为 时(填写有序数对),△ABC关于直线MN对称的△A'B'C'三个顶点都在格点上.
10.(2024秋 廊坊期中)在平面直角坐标系中,点A,B的坐标分别为(3,7),(﹣3,7),则点A,B关于 对称.
11.(2024秋 渠县校级期中)在平面直角坐标系中,将点P先向左平移3个单位长度得到点P1,点P1关于x轴对称的点为P2,已知P2坐标为(﹣2,﹣3),则点P的坐标是 .
三.解答题(共5小题)
12.(2024秋 越秀区校级期中)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1),△ABC关于x轴的对称图形为△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1,B1,C1的坐标.
13.(2024秋 东港市期中)如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 .
14.(2024秋 和平区期中)图①、图②、图③均是3×3的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作格点图形.
(1)在图①中,作△ABC,使其面积为;
(2)在图②中,作四边形ABEF,使其是轴对称图形且面积为3.
15.(2024秋 恩平市期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2024的值.
16.(2024秋 南岗区校级期中)如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上,A(﹣3,3),B(﹣4,﹣2),C(0,﹣1).
(1)直接写出△ABC的面积为 ;
(2)画出△ABC关于y轴的对称的△DEC(点D与点A对应,点E与点B对应),点E的坐标为 ;
(3)用无刻度的直尺,运用所学的知识作出△ABC的高线AF(保留作图痕迹并写出理由).
新课预习衔接 画轴对称图形
参考答案与试题解析
一.选择题(共6小题)
1.(2024秋 蓝田县期中)在平面直角坐标系中,若点A(a,3)与点B(﹣2,b)关于y轴对称,则点M(b,a)所在的象限是( )
A.第二象限 B.第四象限 C.第一象限 D.第三象限
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】C
【分析】根据关于y轴对称的点的坐标特点解答即可.
【解答】解:由题意,得a=2,b=3,
故M(b,a)即M(3,2)在第一象限,
故选:C.
【点评】此题考查关于y轴对称的点的坐标,熟知关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变是解题的关键.
2.(2024秋 雁塔区校级期中)在平面直角坐标系中,点A(﹣2,m﹣1)与点B(n+4,3)关于x轴对称,则的值是( )
A.﹣8 B.2 C. D.﹣2
【考点】关于x轴、y轴对称的点的坐标;立方根.
【专题】平面直角坐标系;运算能力.
【答案】D
【分析】根据关于x轴对称点的坐标性质“横坐标相等,纵坐标互为相反数”,求解即可.
【解答】解:由题意可得:n+4=﹣2,m﹣1=﹣3,
解得n=﹣6,m=﹣2,
∴2.
故选:D.
【点评】本题考查了关于x轴、y轴对称的点的坐标,熟练掌握关于x轴、y轴对称的点的坐标的特点是解题的关键.
3.(2024秋 文峰区期末)如果点P(2,b)和点Q(a,﹣3)关于x轴对称,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系.
【答案】D
【分析】直接利用关于x轴对称点的性质得出a,b的值,进而得出答案.
【解答】解:∵点P(2,b)和点Q(a,﹣3)关于x轴对称,
∴a=2,b=3,
则a+b的值是:5.
故选:D.
【点评】此题主要考查了关于x轴对称点的性质,正确记忆横纵坐标的关系是解题关键.
4.(2024秋 五华区校级期中)剪纸是中国古代最古老的民间艺术之一,其中蕴含着图形的变换.如图是一张蕴含着轴对称变换的蝴蝶剪纸,点A与点B对称,点C与点D对称,将其放置在直角坐标系中,点A,B,C的坐标分别为(2,0),(4,0),(0.5,4),则点D的坐标为( )
A.(3.5,4) B.(5.5,4) C.(5,4) D.(6,4)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平移、旋转与对称;运算能力.
【答案】B
【分析】由点A与点B对称,求得对称轴为直线x=3,再根据点C与点D对称,即可求解.
【解答】解:∵(2,0)与(4,0)对称,
∴对称轴为直线,
∵C(0.5,4)与点D关于直线x=3对称,
∴点D的坐标为(5.5,4).
故选:B.
【点评】本题考查了轴对称的性质,熟练掌握对称点到对称轴的距离相等是解答本题的关键.
5.(2024秋 市南区校级期中)如图,战机在空中展示的图形是轴对称队形,以飞机B,C所在直线为x轴、队形的对称轴为y轴,建立平面直角坐标系.若飞机E的坐标为(50,m),则飞机D的坐标为( )
A.(﹣50,m) B.(50,﹣m) C.(﹣50,﹣m) D.(m,﹣50)
【考点】坐标与图形变化﹣对称;坐标确定位置.
【专题】平面直角坐标系;平移、旋转与对称;几何直观.
【答案】A
【分析】根据轴对称的性质即可得到结论.
【解答】解:∵飞机E(50,m)与飞机D关于y轴对称,
∴飞机D的坐标为(﹣50,m),
故选:A.
【点评】本题考查了坐标与图形变化﹣对称,熟练掌握轴对称的性质是解题的关键.
6.(2024 龙岩模拟)平面直角坐标系xOy中,A(1,0),,则坐标原点O关于直线AB对称的点O′的坐标为( )
A.(2,1) B.
C. D.
【考点】坐标与图形变化﹣对称.
【专题】平移、旋转与对称;推理能力.
【答案】B
【分析】设直线AB的解析式为y=kx+b(k≠0),利用待定系数法求出直线AB的解析式,再由坐标原点O关于直线AB对称的点为O′,可得出直线OO′的解析式,求出直线AB与直线OO′的交点坐标,再利用中点坐标公式即可得出点O′的坐标.
【解答】解:设直线AB的解析式为y=kx+b(k≠0),
∵A(1,0),,
∴,
解得,
∴直线AB的解析式为yx,
∵坐标原点O关于直线AB对称的点为O′,
∴直线OO′的解析式为yx,
∴,
解得,
∴直线AB与直线OO′的交点坐标为(,),
设点O′(a,b),则,,
∴a,b,
∴O′(,).
故选:B.
【点评】本题考查的是坐标与图形变化﹣对称,熟知轴对称的性质是解题的关键.
二.填空题(共5小题)
7.(2024秋 闽侯县期中)在平面直角坐标系xOy中,若A(m,4),B(2,m﹣2n)两点关于x轴对称,则mn的值为 8 .
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】见试题解答内容
【分析】根据关于x轴对称的点,横坐标相同,纵坐标互为相反数,可得答案.
【解答】解:∵A(m,4),B(2,m﹣2n)两点关于x轴对称,
∴m=2,m﹣2n=﹣4,
解得m=2,n=3,
∴mn=23=8.
故答案为:8.
【点评】本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
8.(2024秋 河西区期中)点M(1,﹣6)关于y轴对称的点的坐标为 (﹣1,﹣6) .
【考点】关于x轴、y轴对称的点的坐标.
【专题】平面直角坐标系;符号意识.
【答案】(﹣1,﹣6).
【分析】关于y轴的对称点的坐标特点为:横坐标互为相反数,纵坐标不变,据此求解即可.
【解答】解:点M(1,﹣6)关于y轴对称的点的坐标为(﹣1,﹣6).
故答案为:(﹣1,﹣6).
【点评】本题主要考查了关于x轴、y轴对称的点的坐标,掌握平面直角坐标系中对称点的规律是解答本题的关键.
9.(2024秋 成都期中)如图在12×12的表格中记O为(0,0),M(﹣4,3),△ABC三个顶点分别位于格点上,直线l位于格子横线上,N在l的格点上运动,当N为 (﹣1,0) 时(填写有序数对),△ABC关于直线MN对称的△A'B'C'三个顶点都在格点上.
【考点】坐标与图形变化﹣对称.
【专题】平移、旋转与对称;几何直观.
【答案】(﹣1,0).
【分析】根据题意,画出点N符合条件的示意图即可解决问题.
【解答】解:由BC于AC的位置可知,
当MN与直线l的夹角为45°时,A,B,C三个点关于直线MN的对称点都在格点上.
如图所示,
所以点N为(﹣1,0).
故答案为:(﹣1,0).
【点评】本题主要考查了坐标与图形变化﹣对称,熟知图形对称的性质是解题的关键.
10.(2024秋 廊坊期中)在平面直角坐标系中,点A,B的坐标分别为(3,7),(﹣3,7),则点A,B关于 y轴 对称.
【考点】关于x轴、y轴对称的点的坐标.
【专题】平移、旋转与对称;符号意识.
【答案】y轴.
【分析】根据关于y轴对称的点的坐标特点解答即可.
【解答】解:由题意可知,点A,B 的横坐标互为相反数,纵坐标相同,
∴点 A,B 关于y轴对称.
故答案为:y轴.
【点评】本题考查了关于x,y轴对称的点的坐标,熟知关于y轴对称的点,纵坐标相同,横坐标互为相反数是解题的关键.
11.(2024秋 渠县校级期中)在平面直角坐标系中,将点P先向左平移3个单位长度得到点P1,点P1关于x轴对称的点为P2,已知P2坐标为(﹣2,﹣3),则点P的坐标是 (1,3) .
【考点】关于x轴、y轴对称的点的坐标;坐标与图形变化﹣平移.
【专题】平面直角坐标系;应用意识.
【答案】(1,3).
【分析】注意求原来点的坐标让平移的方向相反即可.根据关于x轴对称的点,横坐标不变,纵坐标变为相反数,可得出P1的坐标,再将P1向平移4个单位长度可得出P的坐标.
【解答】解:∵点P1与P2(﹣2,﹣3)关于x轴对称,
∴P1的坐标为(﹣2,3);
又∵点P先向左平移3个单位长度得到点P1,
∴点P1(﹣2,3)先向右平移3个单位长度得到点P(1,3),
故答案为:(1,3).
【点评】本题考查坐标的平移、对称,掌握平移和对称的规律是解题的关键,注意平移规律:左右平移只改变点的横坐标,左减右加;两点关于x轴对称,横坐标不变,纵坐标互为相反数.
三.解答题(共5小题)
12.(2024秋 越秀区校级期中)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1),△ABC关于x轴的对称图形为△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1,B1,C1的坐标.
【考点】作图﹣轴对称变换;坐标与图形性质.
【专题】作图题;几何直观.
【答案】(1)见解析;
(2)A1(4,0),B1(﹣1,﹣4),C1(﹣3,﹣1).
【分析】(1)根据关于x轴对称的点的横坐标相同,纵坐标互为相反数找到A、B、C对顶点A1、B1、C1的位置,然后顺次连接即可得出△A1B1C1,由图即可得出A1、B1、C1的坐标;
(2)根据A1、B1、C1的位置,直接写出点的坐标即可.
【解答】解:(1)如图,△A1B1C1即为所求,
(2)点A1(4,0),B1(﹣1,﹣4),C1(﹣3,﹣1).
【点评】本题考查了作图—轴对称变换、坐标与图形、割补法求三角形面积,熟练掌握轴对称的性质是解此题的关键.
13.(2024秋 东港市期中)如图,在直角坐标平面内,已知点A(﹣4,1),B(﹣2,4),C(﹣1,2),点P(m+4,﹣5m﹣6),PB平行于x轴.
(1)求出点P的坐标;
(2)画出△ABC关于y轴对称的△A1B1C1;
(3)在y轴上找一点Q,使得2S△BCP=S△BPQ,请直接写出点Q的坐标 (0,0)或(0,8) .
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)P(2,4);
(2)见解析;
(3)(0,0)或(0,8).
【分析】(1)由PB平行于x轴,可得﹣5m﹣6=4,进而求得m的值即可求解;
(2)利用轴对称变换的性质作出A,B,C的对应点A1,B1,C1,再依次连接即可;
(3)设Q(0,m),根据坐标可得S△BCPPB |yC﹣yB|4×|2﹣4|=4,解得2S△BCP=S△BPQ建立方程求解即可.
【解答】解:(1)∵B(﹣2,4),点P(m+4,﹣5m﹣6),PB平行于x轴,
∴﹣5m﹣6=4,解得:m=﹣2,则m+4=2,
∴P(2,4);
(2)如图所示;
(3)∵B(﹣2,4),C(﹣1,2),P(2,4),设Q(0,n),
∴BP=4,
则S△BCPPB |yC﹣yB|4×|2﹣4|=4,
∵2S△BCP=S△BPQ,
∴S△BPQBP|yQ﹣yB|4×|n﹣4|=8,
即:|n﹣4|=4,
∴n=0或n=8,
∴点Q的坐标为(0,0)或(0,8);
故答案为:(0,0)或(0,8).
【点评】本题考查作图—轴对称变换,三角形的面积,图形与坐标,解题的关键是解题的关键是掌握相关知识的灵活运用.
14.(2024秋 和平区期中)图①、图②、图③均是3×3的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.点A、B均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作格点图形.
(1)在图①中,作△ABC,使其面积为;
(2)在图②中,作四边形ABEF,使其是轴对称图形且面积为3.
【考点】作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)见解答.
(2)见解答.
【分析】(1)根据题意,画底为3,高为1的三角形即可.
(2)根据轴对称图形的定义按要求画图即可.
【解答】解:(1)如图①,△ABC即为所求(答案不唯一).
(2)如图②,四边形ABEF即为所求.
【点评】本题考查作图﹣轴对称变换,熟练掌握轴对称图形的定义是解答本题的关键.
15.(2024秋 恩平市期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求(4a+b)2024的值.
【考点】关于x轴、y轴对称的点的坐标;代数式求值.
【专题】平面直角坐标系;应用意识.
【答案】(1)a=﹣8,b=﹣5;
(2)1.
【分析】(1)根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程组求解即可;
(2)根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”列方程组求出a、b的值,然后代入代数式进行计算即可.
【解答】解:(1)∵点A、B关于x轴对称,
∴,
解得,
∴a=﹣8,b=﹣5;
(2)∵点A、B关于y轴对称,
∴,
解得,
∴(4a+b)2024=(﹣4+3)2024=1.
【点评】本题考查了关于x轴、y轴对称的点的坐标,代数式求值,解题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数.
16.(2024秋 南岗区校级期中)如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上,A(﹣3,3),B(﹣4,﹣2),C(0,﹣1).
(1)直接写出△ABC的面积为 9.5 ;
(2)画出△ABC关于y轴的对称的△DEC(点D与点A对应,点E与点B对应),点E的坐标为 (4,﹣2) ;
(3)用无刻度的直尺,运用所学的知识作出△ABC的高线AF(保留作图痕迹并写出理由).
【考点】作图﹣轴对称变换;三角形的角平分线、中线和高.
【专题】作图题;几何直观.
【答案】(1)9.5;
(2)(4,﹣2),
(3)见解析.
【分析】(1)用矩形的面积减去四周三个三角形的面积即可;
(2)分别作出点A、B关于y轴的对称点,再与点C首尾顺次连接即可;
(3)根据网格特点找到点E,连接AE交BC于一点F,于是得到结论.
【解答】解:(1)△ABC的面积为4×51×53×41×4=9.5,
故答案为:9.5;
(2)如图所示,△DEC即为所求,点E的坐标为(4,﹣2),
(3)如图所示,AF即为所求.
∵△AEH≌△CGB(SSS),
∴∠BCG=∠ECH,
∵∠AEH=∠CEF,
∴∠AHE=∠CFE=90°,
∴AF⊥BC.
【点评】本题主要考查作图—轴对称变换,解题的关键是掌握轴对称变换的定义与性质,并据此得出变换后的对应点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
