【新课预习衔接】24.1圆的有关性质(培优卷.含解析)-2025-2026学年九年级上册数学人教版
文档属性
| 名称 | 【新课预习衔接】24.1圆的有关性质(培优卷.含解析)-2025-2026学年九年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 401.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:15:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
新课预习衔接 圆的有关性质
一.选择题(共5小题)
1.(2024秋 西城区校级期中)如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
2.(2024秋 永嘉县期中)如图,点A、B、C在⊙O上,已知∠B=30°,则∠AOC的度数是( )
A.30° B.50° C.40° D.60°
3.(2024 广西模拟)如图,四边形ABCD内接于⊙O,若∠C=125°,则∠A的度数为( )
A.25° B.30° C.50° D.55°
4.(2024 柯桥区二模)某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小敏同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于A、B、C、D四点,然后利用刻度尺量得该纸条的宽为3.5cm,AB=4cm,CD=3cm.请你帮忙计算纸杯杯底的直径为( )
A.4.8cm B.5cm C.5.2cm D.6cm
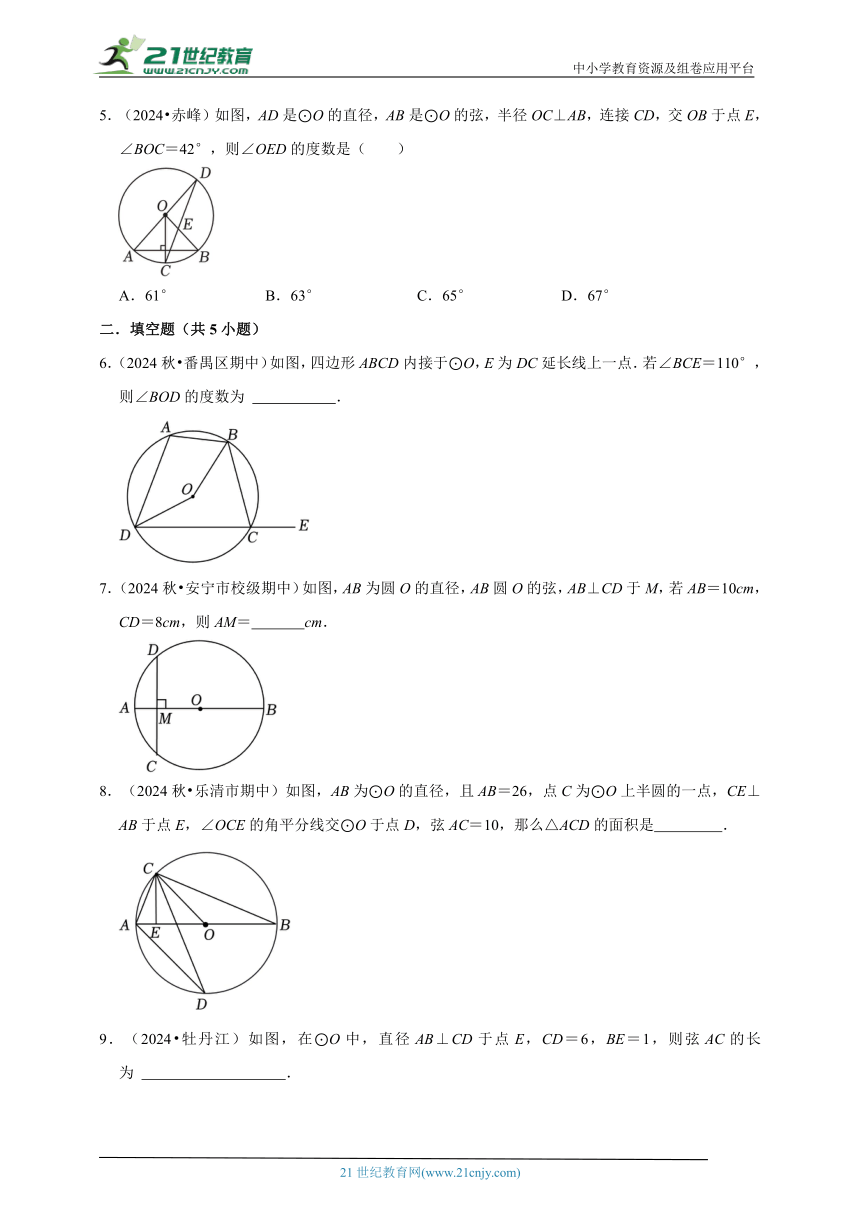
5.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
二.填空题(共5小题)
6.(2024秋 番禺区期中)如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠BCE=110°,则∠BOD的度数为 .
7.(2024秋 安宁市校级期中)如图,AB为圆O的直径,AB圆O的弦,AB⊥CD于M,若AB=10cm,CD=8cm,则AM= cm.
8.(2024秋 乐清市期中)如图,AB为⊙O的直径,且AB=26,点C为⊙O上半圆的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=10,那么△ACD的面积是 .
9.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
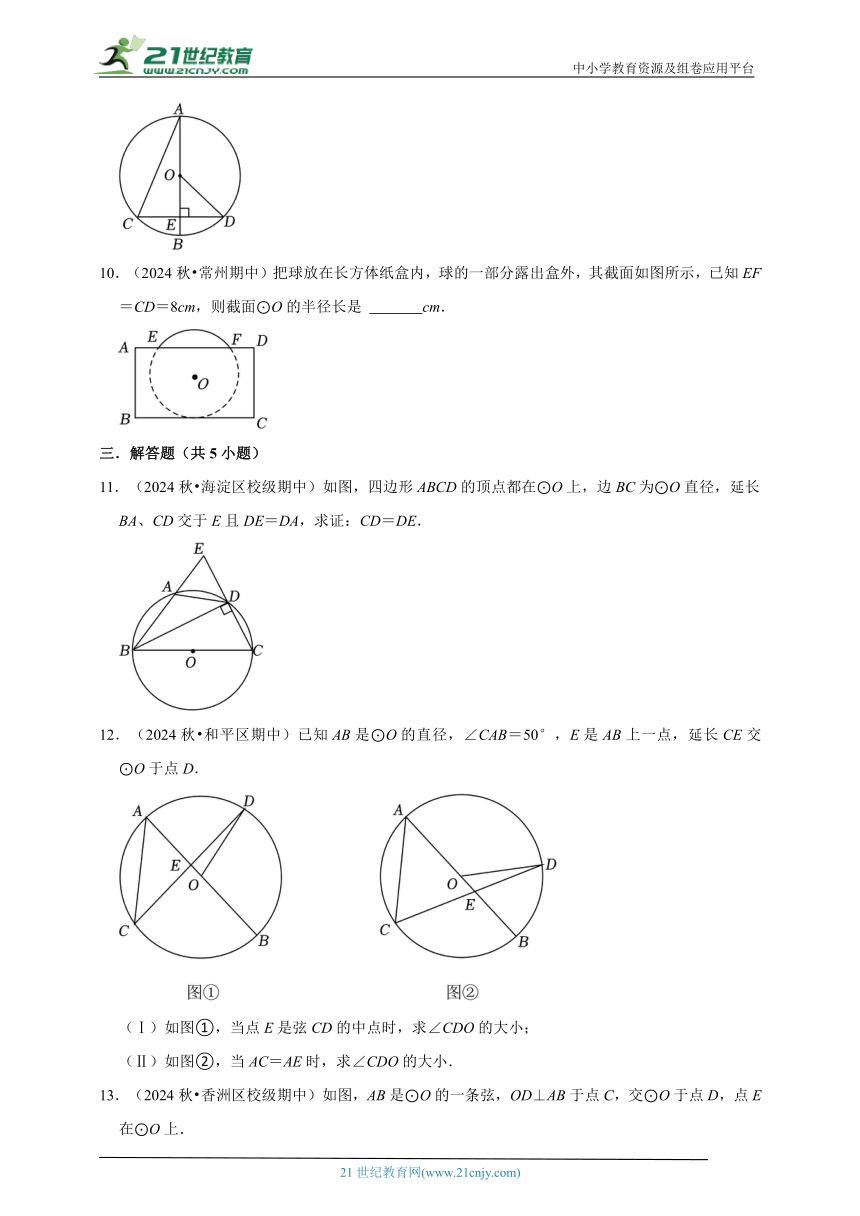
10.(2024秋 常州期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=8cm,则截面⊙O的半径长是 cm.
三.解答题(共5小题)
11.(2024秋 海淀区校级期中)如图,四边形ABCD的顶点都在⊙O上,边BC为⊙O直径,延长BA、CD交于E且DE=DA,求证:CD=DE.
12.(2024秋 和平区期中)已知AB是⊙O的直径,∠CAB=50°,E是AB上一点,延长CE交⊙O于点D.
(Ⅰ)如图①,当点E是弦CD的中点时,求∠CDO的大小;
(Ⅱ)如图②,当AC=AE时,求∠CDO的大小.
13.(2024秋 香洲区校级期中)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上.
(1)若∠BED=28°,则∠AOD的度数为 ;
(2)若点B是的中点,求证:DE=AB;
(3)若CD=3,AB=12,求⊙O的半径长.
14.(2024秋 浦东新区期中)如图,AB,AC是⊙O的两条弦,且.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
15.(2024秋 百色期末)“筒车”是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB为6米时,水面下盛水筒的最大深度为1米(即水面下方圆上部分一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时,则水面上涨的高度为多少米?
新课预习衔接 圆的有关性质
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 西城区校级期中)如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】C
【分析】根据等腰三角形的性质求出∠A=∠AEC=65°,根据圆周角定理得出∠ACB=90°,∠ACE=∠ABD=50°,再直角三角形的性质求出∠ABC的度数,由BE=BC得出∠BCE的度数,再根据角的和差求解即可.
【解答】解:∵CA=CE,∠ACE=50°,
∴∠A=∠AEC(180°﹣∠ACE)=65°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠ABC=25°,
∵∠ACE=∠ABD=50°,
∴∠CBD=∠ABC+∠ABD=75°,
故选:C.
【点评】本题主要考查的是圆周角定理等知识,熟知半圆(或直径)所对的圆周角是直角是解题的关键.
2.(2024秋 永嘉县期中)如图,点A、B、C在⊙O上,已知∠B=30°,则∠AOC的度数是( )
A.30° B.50° C.40° D.60°
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】D
【分析】直接根据圆周角定理解答即可.
【解答】解:∵∠B与∠AOC是同弧所对的圆周角与圆心角,∠B=30°,
∴∠AOC=2∠B=2×30°=60°.
故选:D.
【点评】本题考查的是圆周角定理及圆心角、弧、弦的关系,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.
3.(2024 广西模拟)如图,四边形ABCD内接于⊙O,若∠C=125°,则∠A的度数为( )
A.25° B.30° C.50° D.55°
【考点】圆内接四边形的性质;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据圆内接四边形的对角互补计算即可.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=125°,
∴∠A=55°,
故选:D.
【点评】本题考查的是圆内接四边形的性质,熟记圆内接四边形的对角互补是解题的关键.
4.(2024 柯桥区二模)某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小敏同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于A、B、C、D四点,然后利用刻度尺量得该纸条的宽为3.5cm,AB=4cm,CD=3cm.请你帮忙计算纸杯杯底的直径为( )
A.4.8cm B.5cm C.5.2cm D.6cm
【考点】垂径定理;勾股定理.
【专题】与圆有关的计算;推理能力.
【答案】B
【分析】由垂径定理求出BN,DM的长,设OM=x,由勾股定理得到x2+22=(3.5﹣x)2+1.52,求出x的值,得到OM的长,由勾股定理求出OD长,即可求出纸杯的直径长.
【解答】解:如图,MN⊥AB,MN过圆心O,连接OD,OB,
∴MN=3.5cm,
∵CD∥AB,纸条的宽为3.5cm,AB=3cm,CD=4cm,
∴MN⊥CD,
∴DMCD4=2(cm),BNAB3=1.5(cm),
设OM=x cm,
∴ON=MN﹣OM=(3.5﹣x)cm,
∵OM2+MD2=OD2,ON2+BN2=OB2,
∴OM2+MD2=ON2+BN2,
∴x2+22=(3.5﹣x)2+1.52,
∴x=1.5,
∴OM=1.5(cm),
∴OD2.5(cm),
∴纸杯的直径为2.5×2=5(cm).
故选:B.
【点评】本题考查垂径定理及勾股定理,解题的关键是通过作辅助线构造直角三角形,由垂径定理,勾股定理求出OM的长.
5.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】B
【分析】根据垂径定理得,所以∠AOC=∠BOC=42°,根据圆周角定理得∠D∠AOC=21°,再根据OC=OD,∠C=∠D=21°,最后根据三角形的外角的性质即可得出答案.
【解答】解:∵半径OC⊥AB,
∴,
∴∠AOC=∠BOC=42°,
∴∠D∠AOC=21°,
∵OC=OD,
∴∠C=∠D=21°,
∴∠OED=∠C+∠BOC=21°+42°=63°.
故选:B.
【点评】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握圆周角定理和垂径定理是解题的关键.
二.填空题(共5小题)
6.(2024秋 番禺区期中)如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠BCE=110°,则∠BOD的度数为 140° .
【考点】圆内接四边形的性质;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】140°.
【分析】根据邻补角的定义求出∠BCD,再根据圆周角定理计算即可.
【解答】解:∵∠BCE=110°,
∴∠BCD=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠BCD=140°,
故答案为:140°.
【点评】本题考查的是圆内接四边形,掌握圆周角定理是解题的关键.
7.(2024秋 安宁市校级期中)如图,AB为圆O的直径,AB圆O的弦,AB⊥CD于M,若AB=10cm,CD=8cm,则AM= 2 cm.
【考点】垂径定理;勾股定理.
【专题】圆的有关概念及性质;运算能力.
【答案】2.
【分析】连接OD,首先利用垂径定理求得DM的长,然后在直角△DOM中,利用勾股定理求得OM的长,则AM的长度即可得到.
【解答】解:连接OD,如图,
∵半径AO⊥CD于M,
∴ 8=4(cm),
∵AB=10cm,
∴ 10=5(cm),
在Rt△DOM中,OM3(cm),
则AM=OA﹣OM=5﹣3=2(cm).
故答案为:2.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
8.(2024秋 乐清市期中)如图,AB为⊙O的直径,且AB=26,点C为⊙O上半圆的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=10,那么△ACD的面积是 85 .
【考点】圆周角定理;勾股定理;垂径定理.
【专题】圆的有关概念及性质;运算能力.
【答案】85.
【分析】连接OD,过点A作AF⊥CD,垂足为F,根据直径所对的圆周角是直角可得∠ACB=90°,从而可得∠ACE+∠ECB=90°,再根据垂直定义可得∠CEB=90°,从而可得∠CBE+∠ECB=90°,进而可得∠ACE=∠CBE,再利用等腰三角形的性质以及等量代换可得∠ACE=∠OCB,然后利用角平分线的定义可得∠OCD=∠ECD,从而利用等式的性质可得∠ACD=45°,进而可得∠AOD=2∠ACD=90°,最后在Rt△ACF中,利用锐角三角函数的定义求出AF,CF的长,再在Rt△AOD中,利用等腰直角三角形的性质求出AD的长,从而在Rt△ADF中,利用勾股定理求出DF的长,进而求出CD的长,利用三角形的面积公式进行计算即可解答.
【解答】解:连接OD,过点A作AF⊥CD,垂足为F,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACE+∠ECB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠CBE+∠ECB=90°,
∴∠ACE=∠CBE,
∵OB=OC,
∴∠CBE=∠OCB,
∴∠ACE=∠OCB,
∵CD平分∠OCE,
∴∠OCD=∠ECD,
∴∠ACE+∠DCE=∠OCB+∠OCD∠ACB=45°,
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,
在Rt△ACF中,AC=10,
∴AF=AC sin45°=105,
CF=AC cos45°=105,
在Rt△AOD中,AO=ODAB=13,
∴ADAO=13,
∴DF12,
∴CD=CF+DF=17,
∴△ACD的面积CD AF17585.
故答案为:85.
【点评】此题考查了圆周角定理、勾股定理、三角形面积公式等知识,熟练掌握圆周角定理、勾股定理、三角形面积公式并作出合理的辅助线是解题的关键.
9.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
【考点】圆周角定理;勾股定理;垂径定理.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】.
【分析】由垂径定理得,设⊙O的半径为r,则O E=O B﹣E B=r﹣1,在Rt△OED中,由勾股定理得出方程,求出r=5,即可得出AE=9,在Rt△AEC中,由勾股定理即可求解.
【解答】解:∵A B⊥C D,C D=6,
∴,
设⊙O的半径为r,则O E=O B﹣E B=r﹣1,
在Rt△OED中,由勾股定理得:OE2+DE2=OD2,即(r﹣1)2+32=r2,
解得:r=5,
∴OA=5,OE=4,
∴AE=OA+OE=9,
在Rt△AEC中,由勾股定理得:,
故答案为:.
【点评】本题考查了垂径定理和勾股定理等知识,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
10.(2024秋 常州期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=8cm,则截面⊙O的半径长是 5 cm.
【考点】垂径定理的应用.
【专题】与圆有关的计算;运算能力.
【答案】5.
【分析】过点O作OG⊥EF交EF于点G,连接OE.设OE=r cm,根据垂径定理求出EG,用含r的代数式表示出OG,在Rt△OGE中利用勾股定理列关于r的方程并求解即可.
【解答】解:过点O作OG⊥EF交EF于点G,连接OE.
设OE=r cm,
∵OG⊥EF,EF=CD=8cm,
∴EGEF=4cm,OG=(8﹣r)cm,
在Rt△OGE中利用勾股定理,得OG2+EG2=OE2,
∴(8﹣r)2+42=r2,
∴r=5,
∴截面⊙O的半径长是5cm.
故答案为:5.
【点评】本题考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
三.解答题(共5小题)
11.(2024秋 海淀区校级期中)如图,四边形ABCD的顶点都在⊙O上,边BC为⊙O直径,延长BA、CD交于E且DE=DA,求证:CD=DE.
【考点】圆周角定理;圆内接四边形的性质;等腰三角形的判定与性质.
【专题】与圆有关的计算;运算能力.
【答案】见解析.
【分析】根据等边对等角和圆内接四边形的性质等可得出∠C=∠E,根据等角对等边得出BC=BE,根据圆周角定理可得出BD⊥CE,最后根据等腰三角形三线合一即可得证.
【解答】证明:∵DE=DA,
∴∠E=∠EAD,
∵四边形ABCD的顶点都在⊙O上,∠EAD+∠BAD=180°,
∴∠C+∠BAD=180°,
∴∠EAD=∠C,
∴∠C=∠E,
∴BC=BE,
∴△BCE是等腰三角形,
∵BC为⊙O直径,
∴∠BDC=90°,
∴BD⊥CE,
∴CD=DE.
【点评】本题考查了圆周角定理,掌握圆内接四边形的性质,等腰三角形的判定与性质等知识是解题的关键.
12.(2024秋 和平区期中)已知AB是⊙O的直径,∠CAB=50°,E是AB上一点,延长CE交⊙O于点D.
(Ⅰ)如图①,当点E是弦CD的中点时,求∠CDO的大小;
(Ⅱ)如图②,当AC=AE时,求∠CDO的大小.
【考点】圆周角定理;垂径定理.
【专题】圆的有关概念及性质;运算能力.
【答案】(Ⅰ)10°;
(Ⅱ)15°.
【分析】(Ⅰ)根据垂径定理的推论得CD⊥AB,可得∠C=90°﹣50°=40°,根据圆周角定理得∠DOE=2∠C=80°,即可得出答案;
(Ⅱ)如图②,连接BD,根据等边对等角得∠C=∠AEC=65°,根据圆周角定理的推论得∠B=∠C=65°,∠CDB=∠CAB=50°,利用同圆的半径相等知OB=OD,得∠ODB=∠B=65°,由此可得答案.
【解答】解:(Ⅰ)∵AB是直径,点E是弦CD的中点,
∴CD⊥AB,
∴∠AEC=∠DEO=90°,
∵∠CAB=50°,
∴∠C=40°,
∴∠DOE=2∠C=80°,
∴∠CDO=10°;
(Ⅱ)如图②,连接BD,
∵AC=AE,∠A=50°,
∴∠C=∠AEC=65°,
∴∠B=∠C=65°,
∵OB=OD,
∴∠ODB=∠B=65°,
∵∠CDB=∠CAB=50°,
∴∠CDO=∠ODB﹣∠CDB=65°﹣50°=15°.
【点评】本题考查了垂径定理,圆周角定理,熟练掌握垂径定理,圆周角定理及其推论是关键,注意运用同弧所对的圆周角相等.
13.(2024秋 香洲区校级期中)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上.
(1)若∠BED=28°,则∠AOD的度数为 56° ;
(2)若点B是的中点,求证:DE=AB;
(3)若CD=3,AB=12,求⊙O的半径长.
【考点】圆周角定理;勾股定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】(1)56°;
(2)见解析;
(3)⊙O的半径长为.
【分析】(1)利用垂径定理可以得到弧AD和弧BD相等,然后利用圆周角定理求得∠AOD的度数即可;
(2)由点B是的中点得,根据垂径定理得,则,由圆心角、弧、弦的关系即可得出结论;
(3)利用垂径定理在直角三角形OAC中求得AO的长即可.
【解答】(1)解:∵OD⊥AB于点C,交⊙O于点D,
∴弧AD=弧BD,
∵∠DEB=28°,
∴∠AOD=2∠DEB=56°,
故答案为:56°;
(2)证明:∵点B是的中点,
∴,
∵OD⊥AB于点C,交⊙O于点D,
∴,
∴,
即,
∴DE=AB;
(3)解:∵OD⊥AB,
∴AC=BCAB12=6,
∵CD=3,
∴OC=OD﹣CD=OA﹣CD,
在直角三角形AOC中,AO2=OC2+AC2,
∴AO2=(OA﹣3)2+62,
解得AO,
∴⊙O的半径长为.
【点评】本题考查了圆心角、弧、弦的关系,圆周角定理及垂径定理,勾股定理等知识,解题的关键是利用垂径定理构造直角三角形.
14.(2024秋 浦东新区期中)如图,AB,AC是⊙O的两条弦,且.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【考点】圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;几何直观.
【答案】见试题解答内容
【分析】(1)已知得到AB=AC,又OC=OB,OA=OA,则△AOB≌△AOC,根据全等三角形的性质知,∠1=∠2,进而解答即可;
(2)根据勾股定理解答即可.
【解答】证明:(1)连接OB、OC,
∵.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
【点评】本题主要考查了全等三角形的判定和性质,利用圆中半径相等的隐含条件,获得全等的条件,从而利用全等的性质解决问题.
15.(2024秋 百色期末)“筒车”是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB为6米时,水面下盛水筒的最大深度为1米(即水面下方圆上部分一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时,则水面上涨的高度为多少米?
【考点】垂径定理的应用.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;运算能力;推理能力.
【答案】(1)5m;
(2)1m.
【分析】(1根据垂径定理,勾股定理列方程求解即可;
(2)根据垂径定理、勾股定理求出OG,进而计算出CG即可.
【解答】解:(1)如图,过点O作OD⊥AB,垂足为点C,交⊙O以点D,由题意可知,CD=1m,AB=6m,
∴OC⊥AB,AB=6m,
∴AC=BCAB=3m,
设圆的半径为r m,即OA=OD=r m,OC=(r﹣1)m,
在 Rt△AOC中,
OC2+AC2=OA2,即 (r﹣1)2+32=r2,
解得r=5,
即该圆的半径为5m;
(2)设水面升到如图EF的位置,则EF∥AB,OD与EF相交于点G,
∵OD⊥EF,
∴EG=FGEFm,
连接OE,在Rt△EOG中,OE=5m,EG=4m,
∴OG3m,
∴CG=OC﹣OG=4﹣3=1(m),
即水面上涨的高度为 1 米.
【点评】本题考查垂径定理、勾股定理,掌握垂径定理和勾股定理是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 圆的有关性质
一.选择题(共5小题)
1.(2024秋 西城区校级期中)如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
2.(2024秋 永嘉县期中)如图,点A、B、C在⊙O上,已知∠B=30°,则∠AOC的度数是( )
A.30° B.50° C.40° D.60°
3.(2024 广西模拟)如图,四边形ABCD内接于⊙O,若∠C=125°,则∠A的度数为( )
A.25° B.30° C.50° D.55°
4.(2024 柯桥区二模)某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小敏同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于A、B、C、D四点,然后利用刻度尺量得该纸条的宽为3.5cm,AB=4cm,CD=3cm.请你帮忙计算纸杯杯底的直径为( )
A.4.8cm B.5cm C.5.2cm D.6cm
5.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
二.填空题(共5小题)
6.(2024秋 番禺区期中)如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠BCE=110°,则∠BOD的度数为 .
7.(2024秋 安宁市校级期中)如图,AB为圆O的直径,AB圆O的弦,AB⊥CD于M,若AB=10cm,CD=8cm,则AM= cm.
8.(2024秋 乐清市期中)如图,AB为⊙O的直径,且AB=26,点C为⊙O上半圆的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=10,那么△ACD的面积是 .
9.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
10.(2024秋 常州期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=8cm,则截面⊙O的半径长是 cm.
三.解答题(共5小题)
11.(2024秋 海淀区校级期中)如图,四边形ABCD的顶点都在⊙O上,边BC为⊙O直径,延长BA、CD交于E且DE=DA,求证:CD=DE.
12.(2024秋 和平区期中)已知AB是⊙O的直径,∠CAB=50°,E是AB上一点,延长CE交⊙O于点D.
(Ⅰ)如图①,当点E是弦CD的中点时,求∠CDO的大小;
(Ⅱ)如图②,当AC=AE时,求∠CDO的大小.
13.(2024秋 香洲区校级期中)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上.
(1)若∠BED=28°,则∠AOD的度数为 ;
(2)若点B是的中点,求证:DE=AB;
(3)若CD=3,AB=12,求⊙O的半径长.
14.(2024秋 浦东新区期中)如图,AB,AC是⊙O的两条弦,且.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
15.(2024秋 百色期末)“筒车”是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB为6米时,水面下盛水筒的最大深度为1米(即水面下方圆上部分一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时,则水面上涨的高度为多少米?
新课预习衔接 圆的有关性质
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 西城区校级期中)如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】C
【分析】根据等腰三角形的性质求出∠A=∠AEC=65°,根据圆周角定理得出∠ACB=90°,∠ACE=∠ABD=50°,再直角三角形的性质求出∠ABC的度数,由BE=BC得出∠BCE的度数,再根据角的和差求解即可.
【解答】解:∵CA=CE,∠ACE=50°,
∴∠A=∠AEC(180°﹣∠ACE)=65°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,
∴∠ABC=25°,
∵∠ACE=∠ABD=50°,
∴∠CBD=∠ABC+∠ABD=75°,
故选:C.
【点评】本题主要考查的是圆周角定理等知识,熟知半圆(或直径)所对的圆周角是直角是解题的关键.
2.(2024秋 永嘉县期中)如图,点A、B、C在⊙O上,已知∠B=30°,则∠AOC的度数是( )
A.30° B.50° C.40° D.60°
【考点】圆周角定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】D
【分析】直接根据圆周角定理解答即可.
【解答】解:∵∠B与∠AOC是同弧所对的圆周角与圆心角,∠B=30°,
∴∠AOC=2∠B=2×30°=60°.
故选:D.
【点评】本题考查的是圆周角定理及圆心角、弧、弦的关系,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.
3.(2024 广西模拟)如图,四边形ABCD内接于⊙O,若∠C=125°,则∠A的度数为( )
A.25° B.30° C.50° D.55°
【考点】圆内接四边形的性质;圆周角定理.
【专题】与圆有关的计算;运算能力.
【答案】D
【分析】根据圆内接四边形的对角互补计算即可.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠C+∠A=180°,
∵∠C=125°,
∴∠A=55°,
故选:D.
【点评】本题考查的是圆内接四边形的性质,熟记圆内接四边形的对角互补是解题的关键.
4.(2024 柯桥区二模)某项目化研究小组只用一张矩形纸条和刻度尺,来测量一次性纸杯杯底的直径.小敏同学想到了如下方法:如图,将纸条拉直并紧贴杯底,纸条的上下边沿分别与杯底相交于A、B、C、D四点,然后利用刻度尺量得该纸条的宽为3.5cm,AB=4cm,CD=3cm.请你帮忙计算纸杯杯底的直径为( )
A.4.8cm B.5cm C.5.2cm D.6cm
【考点】垂径定理;勾股定理.
【专题】与圆有关的计算;推理能力.
【答案】B
【分析】由垂径定理求出BN,DM的长,设OM=x,由勾股定理得到x2+22=(3.5﹣x)2+1.52,求出x的值,得到OM的长,由勾股定理求出OD长,即可求出纸杯的直径长.
【解答】解:如图,MN⊥AB,MN过圆心O,连接OD,OB,
∴MN=3.5cm,
∵CD∥AB,纸条的宽为3.5cm,AB=3cm,CD=4cm,
∴MN⊥CD,
∴DMCD4=2(cm),BNAB3=1.5(cm),
设OM=x cm,
∴ON=MN﹣OM=(3.5﹣x)cm,
∵OM2+MD2=OD2,ON2+BN2=OB2,
∴OM2+MD2=ON2+BN2,
∴x2+22=(3.5﹣x)2+1.52,
∴x=1.5,
∴OM=1.5(cm),
∴OD2.5(cm),
∴纸杯的直径为2.5×2=5(cm).
故选:B.
【点评】本题考查垂径定理及勾股定理,解题的关键是通过作辅助线构造直角三角形,由垂径定理,勾股定理求出OM的长.
5.(2024 赤峰)如图,AD是⊙O的直径,AB是⊙O的弦,半径OC⊥AB,连接CD,交OB于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
【考点】圆周角定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;运算能力.
【答案】B
【分析】根据垂径定理得,所以∠AOC=∠BOC=42°,根据圆周角定理得∠D∠AOC=21°,再根据OC=OD,∠C=∠D=21°,最后根据三角形的外角的性质即可得出答案.
【解答】解:∵半径OC⊥AB,
∴,
∴∠AOC=∠BOC=42°,
∴∠D∠AOC=21°,
∵OC=OD,
∴∠C=∠D=21°,
∴∠OED=∠C+∠BOC=21°+42°=63°.
故选:B.
【点评】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦的关系,熟练掌握圆周角定理和垂径定理是解题的关键.
二.填空题(共5小题)
6.(2024秋 番禺区期中)如图,四边形ABCD内接于⊙O,E为DC延长线上一点.若∠BCE=110°,则∠BOD的度数为 140° .
【考点】圆内接四边形的性质;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】140°.
【分析】根据邻补角的定义求出∠BCD,再根据圆周角定理计算即可.
【解答】解:∵∠BCE=110°,
∴∠BCD=180°﹣110°=70°,
由圆周角定理得:∠BOD=2∠BCD=140°,
故答案为:140°.
【点评】本题考查的是圆内接四边形,掌握圆周角定理是解题的关键.
7.(2024秋 安宁市校级期中)如图,AB为圆O的直径,AB圆O的弦,AB⊥CD于M,若AB=10cm,CD=8cm,则AM= 2 cm.
【考点】垂径定理;勾股定理.
【专题】圆的有关概念及性质;运算能力.
【答案】2.
【分析】连接OD,首先利用垂径定理求得DM的长,然后在直角△DOM中,利用勾股定理求得OM的长,则AM的长度即可得到.
【解答】解:连接OD,如图,
∵半径AO⊥CD于M,
∴ 8=4(cm),
∵AB=10cm,
∴ 10=5(cm),
在Rt△DOM中,OM3(cm),
则AM=OA﹣OM=5﹣3=2(cm).
故答案为:2.
【点评】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
8.(2024秋 乐清市期中)如图,AB为⊙O的直径,且AB=26,点C为⊙O上半圆的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=10,那么△ACD的面积是 85 .
【考点】圆周角定理;勾股定理;垂径定理.
【专题】圆的有关概念及性质;运算能力.
【答案】85.
【分析】连接OD,过点A作AF⊥CD,垂足为F,根据直径所对的圆周角是直角可得∠ACB=90°,从而可得∠ACE+∠ECB=90°,再根据垂直定义可得∠CEB=90°,从而可得∠CBE+∠ECB=90°,进而可得∠ACE=∠CBE,再利用等腰三角形的性质以及等量代换可得∠ACE=∠OCB,然后利用角平分线的定义可得∠OCD=∠ECD,从而利用等式的性质可得∠ACD=45°,进而可得∠AOD=2∠ACD=90°,最后在Rt△ACF中,利用锐角三角函数的定义求出AF,CF的长,再在Rt△AOD中,利用等腰直角三角形的性质求出AD的长,从而在Rt△ADF中,利用勾股定理求出DF的长,进而求出CD的长,利用三角形的面积公式进行计算即可解答.
【解答】解:连接OD,过点A作AF⊥CD,垂足为F,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACE+∠ECB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠CBE+∠ECB=90°,
∴∠ACE=∠CBE,
∵OB=OC,
∴∠CBE=∠OCB,
∴∠ACE=∠OCB,
∵CD平分∠OCE,
∴∠OCD=∠ECD,
∴∠ACE+∠DCE=∠OCB+∠OCD∠ACB=45°,
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,
在Rt△ACF中,AC=10,
∴AF=AC sin45°=105,
CF=AC cos45°=105,
在Rt△AOD中,AO=ODAB=13,
∴ADAO=13,
∴DF12,
∴CD=CF+DF=17,
∴△ACD的面积CD AF17585.
故答案为:85.
【点评】此题考查了圆周角定理、勾股定理、三角形面积公式等知识,熟练掌握圆周角定理、勾股定理、三角形面积公式并作出合理的辅助线是解题的关键.
9.(2024 牡丹江)如图,在⊙O中,直径AB⊥CD于点E,CD=6,BE=1,则弦AC的长为 .
【考点】圆周角定理;勾股定理;垂径定理.
【专题】与圆有关的计算;运算能力;推理能力.
【答案】.
【分析】由垂径定理得,设⊙O的半径为r,则O E=O B﹣E B=r﹣1,在Rt△OED中,由勾股定理得出方程,求出r=5,即可得出AE=9,在Rt△AEC中,由勾股定理即可求解.
【解答】解:∵A B⊥C D,C D=6,
∴,
设⊙O的半径为r,则O E=O B﹣E B=r﹣1,
在Rt△OED中,由勾股定理得:OE2+DE2=OD2,即(r﹣1)2+32=r2,
解得:r=5,
∴OA=5,OE=4,
∴AE=OA+OE=9,
在Rt△AEC中,由勾股定理得:,
故答案为:.
【点评】本题考查了垂径定理和勾股定理等知识,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
10.(2024秋 常州期中)把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=8cm,则截面⊙O的半径长是 5 cm.
【考点】垂径定理的应用.
【专题】与圆有关的计算;运算能力.
【答案】5.
【分析】过点O作OG⊥EF交EF于点G,连接OE.设OE=r cm,根据垂径定理求出EG,用含r的代数式表示出OG,在Rt△OGE中利用勾股定理列关于r的方程并求解即可.
【解答】解:过点O作OG⊥EF交EF于点G,连接OE.
设OE=r cm,
∵OG⊥EF,EF=CD=8cm,
∴EGEF=4cm,OG=(8﹣r)cm,
在Rt△OGE中利用勾股定理,得OG2+EG2=OE2,
∴(8﹣r)2+42=r2,
∴r=5,
∴截面⊙O的半径长是5cm.
故答案为:5.
【点评】本题考查垂径定理,掌握垂径定理和勾股定理是解题的关键.
三.解答题(共5小题)
11.(2024秋 海淀区校级期中)如图,四边形ABCD的顶点都在⊙O上,边BC为⊙O直径,延长BA、CD交于E且DE=DA,求证:CD=DE.
【考点】圆周角定理;圆内接四边形的性质;等腰三角形的判定与性质.
【专题】与圆有关的计算;运算能力.
【答案】见解析.
【分析】根据等边对等角和圆内接四边形的性质等可得出∠C=∠E,根据等角对等边得出BC=BE,根据圆周角定理可得出BD⊥CE,最后根据等腰三角形三线合一即可得证.
【解答】证明:∵DE=DA,
∴∠E=∠EAD,
∵四边形ABCD的顶点都在⊙O上,∠EAD+∠BAD=180°,
∴∠C+∠BAD=180°,
∴∠EAD=∠C,
∴∠C=∠E,
∴BC=BE,
∴△BCE是等腰三角形,
∵BC为⊙O直径,
∴∠BDC=90°,
∴BD⊥CE,
∴CD=DE.
【点评】本题考查了圆周角定理,掌握圆内接四边形的性质,等腰三角形的判定与性质等知识是解题的关键.
12.(2024秋 和平区期中)已知AB是⊙O的直径,∠CAB=50°,E是AB上一点,延长CE交⊙O于点D.
(Ⅰ)如图①,当点E是弦CD的中点时,求∠CDO的大小;
(Ⅱ)如图②,当AC=AE时,求∠CDO的大小.
【考点】圆周角定理;垂径定理.
【专题】圆的有关概念及性质;运算能力.
【答案】(Ⅰ)10°;
(Ⅱ)15°.
【分析】(Ⅰ)根据垂径定理的推论得CD⊥AB,可得∠C=90°﹣50°=40°,根据圆周角定理得∠DOE=2∠C=80°,即可得出答案;
(Ⅱ)如图②,连接BD,根据等边对等角得∠C=∠AEC=65°,根据圆周角定理的推论得∠B=∠C=65°,∠CDB=∠CAB=50°,利用同圆的半径相等知OB=OD,得∠ODB=∠B=65°,由此可得答案.
【解答】解:(Ⅰ)∵AB是直径,点E是弦CD的中点,
∴CD⊥AB,
∴∠AEC=∠DEO=90°,
∵∠CAB=50°,
∴∠C=40°,
∴∠DOE=2∠C=80°,
∴∠CDO=10°;
(Ⅱ)如图②,连接BD,
∵AC=AE,∠A=50°,
∴∠C=∠AEC=65°,
∴∠B=∠C=65°,
∵OB=OD,
∴∠ODB=∠B=65°,
∵∠CDB=∠CAB=50°,
∴∠CDO=∠ODB﹣∠CDB=65°﹣50°=15°.
【点评】本题考查了垂径定理,圆周角定理,熟练掌握垂径定理,圆周角定理及其推论是关键,注意运用同弧所对的圆周角相等.
13.(2024秋 香洲区校级期中)如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,点E在⊙O上.
(1)若∠BED=28°,则∠AOD的度数为 56° ;
(2)若点B是的中点,求证:DE=AB;
(3)若CD=3,AB=12,求⊙O的半径长.
【考点】圆周角定理;勾股定理;垂径定理;圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;推理能力.
【答案】(1)56°;
(2)见解析;
(3)⊙O的半径长为.
【分析】(1)利用垂径定理可以得到弧AD和弧BD相等,然后利用圆周角定理求得∠AOD的度数即可;
(2)由点B是的中点得,根据垂径定理得,则,由圆心角、弧、弦的关系即可得出结论;
(3)利用垂径定理在直角三角形OAC中求得AO的长即可.
【解答】(1)解:∵OD⊥AB于点C,交⊙O于点D,
∴弧AD=弧BD,
∵∠DEB=28°,
∴∠AOD=2∠DEB=56°,
故答案为:56°;
(2)证明:∵点B是的中点,
∴,
∵OD⊥AB于点C,交⊙O于点D,
∴,
∴,
即,
∴DE=AB;
(3)解:∵OD⊥AB,
∴AC=BCAB12=6,
∵CD=3,
∴OC=OD﹣CD=OA﹣CD,
在直角三角形AOC中,AO2=OC2+AC2,
∴AO2=(OA﹣3)2+62,
解得AO,
∴⊙O的半径长为.
【点评】本题考查了圆心角、弧、弦的关系,圆周角定理及垂径定理,勾股定理等知识,解题的关键是利用垂径定理构造直角三角形.
14.(2024秋 浦东新区期中)如图,AB,AC是⊙O的两条弦,且.
(1)求证:AO平分∠BAC;
(2)若AB=4,BC=8,求半径OA的长.
【考点】圆心角、弧、弦的关系.
【专题】圆的有关概念及性质;几何直观.
【答案】见试题解答内容
【分析】(1)已知得到AB=AC,又OC=OB,OA=OA,则△AOB≌△AOC,根据全等三角形的性质知,∠1=∠2,进而解答即可;
(2)根据勾股定理解答即可.
【解答】证明:(1)连接OB、OC,
∵.
∴AB=AC,
∵OC=OB,OA=OA,
在△AOB与△AOC中,
.
∴△AOB≌△AOC(SSS),
∴∠1=∠2,
∴AO平分∠BAC;
(2)连接AO并延长交BC于E,连接OB,
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
设OA=x,可得:AB2﹣BE2=AE2,OB2=OE2+BE2,
可得:,x2=OE2+42,OE+x=8,
解得:x=5,OE=3,
∴半径OA的长=5.
【点评】本题主要考查了全等三角形的判定和性质,利用圆中半径相等的隐含条件,获得全等的条件,从而利用全等的性质解决问题.
15.(2024秋 百色期末)“筒车”是一种以水流作动力,取水灌田的工具,据史料记载,它发明于隋而盛于唐,距今已有1000多年的历史,是我国古代劳动人民的一项伟大创造.
如图,“筒车”盛水筒的运行轨迹是以轴心O为圆心的圆,已知圆心O在水面上方,且当圆被水面截得的弦AB为6米时,水面下盛水筒的最大深度为1米(即水面下方圆上部分一点距离水面的最大距离).
(1)求该圆的半径;
(2)若水面上涨导致圆被水面截得的弦AB从原来的6米变为8米时,则水面上涨的高度为多少米?
【考点】垂径定理的应用.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;运算能力;推理能力.
【答案】(1)5m;
(2)1m.
【分析】(1根据垂径定理,勾股定理列方程求解即可;
(2)根据垂径定理、勾股定理求出OG,进而计算出CG即可.
【解答】解:(1)如图,过点O作OD⊥AB,垂足为点C,交⊙O以点D,由题意可知,CD=1m,AB=6m,
∴OC⊥AB,AB=6m,
∴AC=BCAB=3m,
设圆的半径为r m,即OA=OD=r m,OC=(r﹣1)m,
在 Rt△AOC中,
OC2+AC2=OA2,即 (r﹣1)2+32=r2,
解得r=5,
即该圆的半径为5m;
(2)设水面升到如图EF的位置,则EF∥AB,OD与EF相交于点G,
∵OD⊥EF,
∴EG=FGEFm,
连接OE,在Rt△EOG中,OE=5m,EG=4m,
∴OG3m,
∴CG=OC﹣OG=4﹣3=1(m),
即水面上涨的高度为 1 米.
【点评】本题考查垂径定理、勾股定理,掌握垂径定理和勾股定理是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
