【新课预习衔接】24.4弧长和扇形面积(培优卷.含解析)-2025-2026学年九年级上册数学人教版
文档属性
| 名称 | 【新课预习衔接】24.4弧长和扇形面积(培优卷.含解析)-2025-2026学年九年级上册数学人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 328.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 12:07:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
新课预习衔接 弧长和扇形面积
一.选择题(共5小题)
1.(2024秋 无锡期中)“奇妙”手工课堂开课啦!一起动手试试吧:拿出一张正方形的纸片,在上面剪出一个扇形和一个圆,尝试后发现圆恰好是该圆锥的底面.(圆心O2与圆锥顶点同在如图虚线上)测量后得知,圆锥母线长16cm,则以下这张正方形纸片的边长是( )cm.
A. B. C.20 D.
2.(2024秋 海淀区校级期中)如图,⊙O的半径为12,点A、B是圆上的两点,∠AOB=120°,则的长为( )
A.6π B.8π C.10π D.12π
3.(2024秋 沙坪坝区校级期中)如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,分别以B、C为圆心,BC长为半径画弧,交BC于点P,交AB于点M,交AC于点N,则图中阴影部分面积为( )
A. B. C. D.
4.(2024秋 莒县期中)如图,Rt△ABC中,∠C=90°,BC=2,∠A=30°,以点A为圆心、AC为半径画弧,交AB于点E,以点B为圆心、BC为半径画弧,交AB于点F,则阴影部分的面积为( )
A. B. C. D.
5.(2024 广水市模拟)如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接CD与AB交于点E,若BE=BC时,弧BD的长为( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 青秀区校级期中)小李同学在数学综合实践活动中,用一块扇形材料制作了一个圆锥模型(如图所示),经过小黄同学测量得圆锥底面直径为12cm,圆锥的高为8cm,则根据测量数据推算,该圆锥模型的侧面积为 cm2.
7.(2024 金湖县一模)已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是 .
8.(2024秋 南京期中)如图,在△ABC中,AB=AC=6,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则扇形ODE的面积为 .
9.(2024秋 建邺区期中)用半径为5cm,圆心角为72°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥的高为 cm.
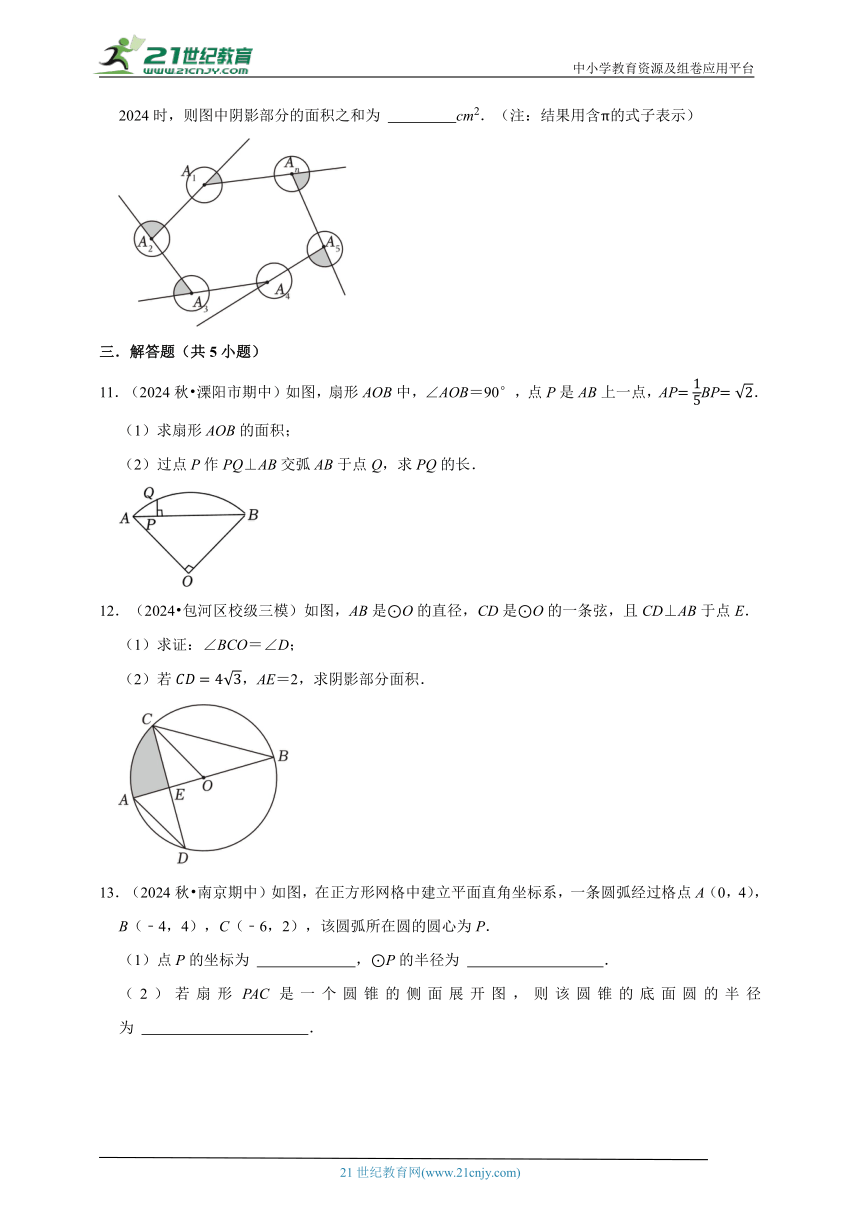
10.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 cm2.(注:结果用含π的式子表示)
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
12.(2024 包河区校级三模)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若,AE=2,求阴影部分面积.
13.(2024秋 南京期中)如图,在正方形网格中建立平面直角坐标系,一条圆弧经过格点A(0,4),B(﹣4,4),C(﹣6,2),该圆弧所在圆的圆心为P.
(1)点P的坐标为 ,⊙P的半径为 .
(2)若扇形PAC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为 .
14.(2024秋 蓬江区校级期中)如图,在△ABC中,∠ACB=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求∠ACD的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积.
15.(2024秋 滨湖区期末)如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
新课预习衔接 弧长和扇形面积
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 无锡期中)“奇妙”手工课堂开课啦!一起动手试试吧:拿出一张正方形的纸片,在上面剪出一个扇形和一个圆,尝试后发现圆恰好是该圆锥的底面.(圆心O2与圆锥顶点同在如图虚线上)测量后得知,圆锥母线长16cm,则以下这张正方形纸片的边长是( )cm.
A. B. C.20 D.
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】根据扇形的弧长等于圆的底面周长,即可求出圆锥底面圆的半径,再求出正方形的对角线的长可得结论.
【解答】解:设圆锥底面圆的半径为r cm,
由题意2πr,
∴r=4,
∴正方形的对角线的长=16+4+4(20+4)cm,
∴正方形的边长为(104)cm.
故选:B.
【点评】本题考查了圆锥的计算,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.(2024秋 海淀区校级期中)如图,⊙O的半径为12,点A、B是圆上的两点,∠AOB=120°,则的长为( )
A.6π B.8π C.10π D.12π
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】直接根据弧长公式计算即可.
【解答】解:的长为8π.
故选:B.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
3.(2024秋 沙坪坝区校级期中)如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,分别以B、C为圆心,BC长为半径画弧,交BC于点P,交AB于点M,交AC于点N,则图中阴影部分面积为( )
A. B. C. D.
【考点】扇形面积的计算;勾股定理.
【专题】圆的有关概念及性质;推理能力.
【答案】A
【分析】利用直角三角形的面积减去两个扇形的面积进行求解即可.
【解答】解:∵∠A=90°,AB=4,AC=3,
∴∠B+∠C=90°,,
∵以B、C为圆心,长为半径画弧,
∴扇形CPN和扇形BPM的半径相同,均为,
∴两个扇形的面积之和为,
∴阴影部分的面积为:;
故选:A.
【点评】本题考查求阴影部分的面积,关键是根据直角三角形的面积减去两个扇形的面积解答.
4.(2024秋 莒县期中)如图,Rt△ABC中,∠C=90°,BC=2,∠A=30°,以点A为圆心、AC为半径画弧,交AB于点E,以点B为圆心、BC为半径画弧,交AB于点F,则阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;含30度角的直角三角形;勾股定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力.
【答案】A
【分析】求出∠B,根据三角函数求出AC;利用扇形的面积公式,根据“阴影部分的面积=扇形ACE的面积+扇形BCF的面积﹣三角形ABC的面积”计算即可.
【解答】解:∵∠C=90°,∠A=30°,BC=2,
∴∠B=90°﹣∠A=60°,AC=BC ctan∠A=2×ctan30°=2,
∴S阴影=S扇形ACE+S扇形BCF﹣SRt△ABC
(2)2π22×π22
2,
∴阴影部分的面积为2.
故答案为:A.
【点评】本题考查扇形面积的计算、含30度角的直角三角形、勾股定理,掌握特殊角的三角函数、扇形和三角形面积计算公式是解题的关键.
5.(2024 广水市模拟)如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接CD与AB交于点E,若BE=BC时,弧BD的长为( )
A. B. C. D.
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】B
【分析】根据BE=BC求出∠BOD,利用弧长公式求解即可.
【解答】解:如图1,当BE=BC时,
∵BE=BC,∠ABC=40°,
∴∠BCE=∠BEC(180°﹣40°)=70°,
∴∠BOD=2∠BCE=140°,
∴弧BD的长π.
故选:B.
【点评】本题考查弧长公式,圆周角定理,等腰三角形的性质,三角形内角和定理等知识,解题的关键是根据圆周角定理求出∠BOD=140°.
二.填空题(共5小题)
6.(2024秋 青秀区校级期中)小李同学在数学综合实践活动中,用一块扇形材料制作了一个圆锥模型(如图所示),经过小黄同学测量得圆锥底面直径为12cm,圆锥的高为8cm,则根据测量数据推算,该圆锥模型的侧面积为 60π cm2.
【考点】圆锥的计算.
【专题】展开与折叠;运算能力.
【答案】60π.
【分析】先利用勾股定理计算出圆锥的母线长,再根据扇形的面积公式计算圆锥的侧面积.
【解答】解:根据题意,圆锥的母线长10(cm),
所以该圆锥的侧面积12π×10=60π(cm2).
故答案为:60π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2024 金湖县一模)已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是 15π .
【考点】圆锥的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【解答】解:圆锥的侧面积 2π 3 5=15π.
故答案为15π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
8.(2024秋 南京期中)如图,在△ABC中,AB=AC=6,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则扇形ODE的面积为 π .
【考点】扇形面积的计算;等腰三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OE,OD,由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO,由OE=OA,∠OEA=∠BAC=50°,因此∠EOD=∠BAC=50°,由扇形的面积公式计算即可.
【解答】解:∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO,
∵OE=OA,
∴∠OEA=∠BAC=50°,
∴∠EOD=∠BAC=50°,
∵ODAB=3,
∴扇形ODE的面积为π.
故答案为:.
【点评】本题考查扇形面积的计算,等腰三角形的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
9.(2024秋 建邺区期中)用半径为5cm,圆心角为72°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥的高为 cm.
【考点】圆锥的计算;展开图折叠成几何体.
【专题】圆的有关概念及性质;应用意识.
【答案】.
【分析】根据题意,设圆锥的底面半径为r厘米,这个扇形的弧长等于圆锥的底面周长,根据公式表示出圆的周长和弧长,求出半径,再利用勾股定理,求出圆锥的高,据此解答.
【解答】解:设圆锥的底面半径为r厘米.
,
,
r=1,
圆锥的高为(厘米).
答:这个圆锥的高为cm.
故答案为:.
【点评】本题考查了圆锥的计算、展开图折叠成几何体,解决本题的关键是先求出圆锥的底面半径.
10.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 4π cm2.(注:结果用含π的式子表示)
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】4π.
【分析】由题意得到各顶点的扇形圆心角之和即为n边形外角和,利用扇形面积公式计算即可求出阴影部分面积.
【解答】解:∵n边形的外角和为360°,半径为2cm,
∴S阴影4πcm2,
故答案为:4π.
【点评】此题考查了扇形面积的计算,以及多边形的内角和与外角和,熟练掌握扇形面积公式是解本题的关键.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)9π;
(2).
【分析】(1)依题意得AB,OA=OB,∠AOB=90°,则△OAB是等腰直角三角形,再由勾股定理求出OA=6,进而可得扇形AOB的面积;
(2)过O作OC⊥AB于C,OD⊥PQ交QP的延长线于D,QD交OA于E,证明四边形OCPD为矩形,再根据△OAB是等腰直角三角形得AC=BC=OC,OQ=OA=6,则OD=PC,PD=OC,然后由勾股定理求出DQ,进而可得PQ的长.
【解答】解:(1)∵APBP,
∴AP,BP,
∴AB=AP+BP,
∵OA=OB,∠AOB=90°,
∴△OAB是等腰直角三角形,
由勾股定理得:AB,
∴,
∴OA=6,
∴扇形AOB的面积为:9π;
(2)过点O作OC⊥AB于C,作OD⊥PQ交QP的延长线于D,QD交OA于点E,连接OQ,如图所示:
∵PQ⊥AB,
∴四边形OCPD为矩形,
∴OC=DP,OD=PC,
由(1)知:△OAB是等腰直角三角形,且OA=OB=6,AB,AP,
∴AC=BC=OCAB,OQ=OA=6,
∴OD=PC=AC﹣AP,PD=OC,
在Rt△ODQ中,由勾股定理得:DQ,
∴PQ=DQ﹣PD.
【点评】此题主要考查了扇形面积,熟练掌握扇形的面积公式是解决问题的关键.
12.(2024 包河区校级三模)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若,AE=2,求阴影部分面积.
【考点】扇形面积的计算;勾股定理;垂径定理;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】见试题解答内容
【分析】(1)根据等腰三角形性质求出∠BCO=∠B,根据圆周角定理得出∠B=∠D,再求出答案即可;
(2)根据垂径定理求出CE=2,再根据勾股定理求出OC,进一步即可求得OE,利用直角三角函数求得∠AOC=60°,然后根据S阴影=S扇形AOC﹣S△COE求解即可.
【解答】(1)证明:∵OC=OB,
∴∠BCO=∠B,
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB 是⊙O的直径,CD⊥AB于点E,
∴,
∵,
∴,
在Rt△OCE 中,OC2=CE2+OE2,
∴,
解得:r=4(负数舍去),
∴OC=OA=4,
∴OE=4﹣2=2,
∴tan,
∴∠AOC=60°,
∴S阴影=S扇形AOC﹣S△COEπ﹣2.
【点评】本题考查了扇形的面积,垂径定理,勾股定理,等腰三角形的性质,圆周角定理等知识点,熟练掌握性质定理,明确S阴影=S扇形AOC﹣S△COE是解此题的关键.
13.(2024秋 南京期中)如图,在正方形网格中建立平面直角坐标系,一条圆弧经过格点A(0,4),B(﹣4,4),C(﹣6,2),该圆弧所在圆的圆心为P.
(1)点P的坐标为 (﹣2,0) ,⊙P的半径为 2 .
(2)若扇形PAC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为 .
【考点】圆锥的计算;坐标与图形性质;垂径定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】(1)(﹣2,0),2;
(2).
【分析】(1)根据垂径定理以及勾股定理进行计算即可;
(2)求出扇形PAC的圆心角度数,进而求出弧AC的长,再根据圆锥侧面展开图的特征进行计算即可.
【解答】解:(1)如图,依据网格,作AB,BC的中垂线相交于点P,点P的坐标为(﹣2,0),
PA2,
即⊙P的半径为2,
故答案为:(﹣2,0),2;
(2)如图,易证△AOP≌△PDC(SAS),
∴∠OAP=∠DPC,
∴∠OAP+∠OPA=90°,
∴∠DPC+∠OPA=90°,
∴∠APC=180°﹣90°=90°,
∴的长为π,
设圆锥的底面半径为r,则2πrπ,
解得r,
故答案为:.
【点评】本题考查垂径定理、勾股定理,圆锥的计算,掌握垂径定理、勾股定理以及弧长、圆周长的计算方法是正确解答的关键.
14.(2024秋 蓬江区校级期中)如图,在△ABC中,∠ACB=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求∠ACD的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积.
【考点】扇形面积的计算;直角三角形斜边上的中线;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;推理能力.
【答案】(1)56°;
(2).
【分析】(1)利用直角三角形的两锐角互余计算出∠BAC=62°,然后根据等腰三角形的性质及三角形内角和定理计算出∠ACD的度数;
(2)利用斜边上的中线性质得到CD=AD=BDAB=1,再判断△ACD为等边三角形,则∠ACD=60°,利用扇形的面积公式,根据阴影部分的面积=S扇形ACD进行计算.
【解答】解:(1)∵∠ACB=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵CA=CD,
∴∠CDA=∠CAD=62°,
∴∠ACD=180°﹣62°﹣62°=56°;
(2)∵D是AB的中点,∠ACB=90°,
∴CD=AD=BDAB=1,
∵CD=CA,
∴△ACD为等边三角形,
∴∠ACD=60°,
∴阴影部分的面积=S扇形ACD.
【点评】本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形πR2或S扇形lR(其中l为扇形的弧长).
15.(2024秋 滨湖区期末)如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
【考点】扇形面积的计算;旋转的性质;全等三角形的判定与性质.
【专题】与圆有关的计算.
【答案】见试题解答内容
【分析】(1)证明△ADE≌△BDC(SAS),推出∠ADE=∠BDC,推出即可解决问题.
(2)证明S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF即可解决问题.
【解答】(1)证明:∵AD=BD,∠DAE=∠DBC,AE=BC,
∴△ADE≌△BDC(SAS),
∴∠ADE=∠BDC,
∴.
∴AB=BC.
(2)解:S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF.
【点评】本题考查扇形的面积公式,全等三角形的判定和性质,等腰三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
新课预习衔接 弧长和扇形面积
一.选择题(共5小题)
1.(2024秋 无锡期中)“奇妙”手工课堂开课啦!一起动手试试吧:拿出一张正方形的纸片,在上面剪出一个扇形和一个圆,尝试后发现圆恰好是该圆锥的底面.(圆心O2与圆锥顶点同在如图虚线上)测量后得知,圆锥母线长16cm,则以下这张正方形纸片的边长是( )cm.
A. B. C.20 D.
2.(2024秋 海淀区校级期中)如图,⊙O的半径为12,点A、B是圆上的两点,∠AOB=120°,则的长为( )
A.6π B.8π C.10π D.12π
3.(2024秋 沙坪坝区校级期中)如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,分别以B、C为圆心,BC长为半径画弧,交BC于点P,交AB于点M,交AC于点N,则图中阴影部分面积为( )
A. B. C. D.
4.(2024秋 莒县期中)如图,Rt△ABC中,∠C=90°,BC=2,∠A=30°,以点A为圆心、AC为半径画弧,交AB于点E,以点B为圆心、BC为半径画弧,交AB于点F,则阴影部分的面积为( )
A. B. C. D.
5.(2024 广水市模拟)如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接CD与AB交于点E,若BE=BC时,弧BD的长为( )
A. B. C. D.
二.填空题(共5小题)
6.(2024秋 青秀区校级期中)小李同学在数学综合实践活动中,用一块扇形材料制作了一个圆锥模型(如图所示),经过小黄同学测量得圆锥底面直径为12cm,圆锥的高为8cm,则根据测量数据推算,该圆锥模型的侧面积为 cm2.
7.(2024 金湖县一模)已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是 .
8.(2024秋 南京期中)如图,在△ABC中,AB=AC=6,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则扇形ODE的面积为 .
9.(2024秋 建邺区期中)用半径为5cm,圆心角为72°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥的高为 cm.
10.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 cm2.(注:结果用含π的式子表示)
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
12.(2024 包河区校级三模)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若,AE=2,求阴影部分面积.
13.(2024秋 南京期中)如图,在正方形网格中建立平面直角坐标系,一条圆弧经过格点A(0,4),B(﹣4,4),C(﹣6,2),该圆弧所在圆的圆心为P.
(1)点P的坐标为 ,⊙P的半径为 .
(2)若扇形PAC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为 .
14.(2024秋 蓬江区校级期中)如图,在△ABC中,∠ACB=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求∠ACD的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积.
15.(2024秋 滨湖区期末)如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
新课预习衔接 弧长和扇形面积
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 无锡期中)“奇妙”手工课堂开课啦!一起动手试试吧:拿出一张正方形的纸片,在上面剪出一个扇形和一个圆,尝试后发现圆恰好是该圆锥的底面.(圆心O2与圆锥顶点同在如图虚线上)测量后得知,圆锥母线长16cm,则以下这张正方形纸片的边长是( )cm.
A. B. C.20 D.
【考点】圆锥的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】根据扇形的弧长等于圆的底面周长,即可求出圆锥底面圆的半径,再求出正方形的对角线的长可得结论.
【解答】解:设圆锥底面圆的半径为r cm,
由题意2πr,
∴r=4,
∴正方形的对角线的长=16+4+4(20+4)cm,
∴正方形的边长为(104)cm.
故选:B.
【点评】本题考查了圆锥的计算,圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
2.(2024秋 海淀区校级期中)如图,⊙O的半径为12,点A、B是圆上的两点,∠AOB=120°,则的长为( )
A.6π B.8π C.10π D.12π
【考点】弧长的计算.
【专题】与圆有关的计算;运算能力.
【答案】B
【分析】直接根据弧长公式计算即可.
【解答】解:的长为8π.
故选:B.
【点评】本题考查弧长的计算,关键是掌握弧长公式.
3.(2024秋 沙坪坝区校级期中)如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,分别以B、C为圆心,BC长为半径画弧,交BC于点P,交AB于点M,交AC于点N,则图中阴影部分面积为( )
A. B. C. D.
【考点】扇形面积的计算;勾股定理.
【专题】圆的有关概念及性质;推理能力.
【答案】A
【分析】利用直角三角形的面积减去两个扇形的面积进行求解即可.
【解答】解:∵∠A=90°,AB=4,AC=3,
∴∠B+∠C=90°,,
∵以B、C为圆心,长为半径画弧,
∴扇形CPN和扇形BPM的半径相同,均为,
∴两个扇形的面积之和为,
∴阴影部分的面积为:;
故选:A.
【点评】本题考查求阴影部分的面积,关键是根据直角三角形的面积减去两个扇形的面积解答.
4.(2024秋 莒县期中)如图,Rt△ABC中,∠C=90°,BC=2,∠A=30°,以点A为圆心、AC为半径画弧,交AB于点E,以点B为圆心、BC为半径画弧,交AB于点F,则阴影部分的面积为( )
A. B. C. D.
【考点】扇形面积的计算;含30度角的直角三角形;勾股定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;运算能力.
【答案】A
【分析】求出∠B,根据三角函数求出AC;利用扇形的面积公式,根据“阴影部分的面积=扇形ACE的面积+扇形BCF的面积﹣三角形ABC的面积”计算即可.
【解答】解:∵∠C=90°,∠A=30°,BC=2,
∴∠B=90°﹣∠A=60°,AC=BC ctan∠A=2×ctan30°=2,
∴S阴影=S扇形ACE+S扇形BCF﹣SRt△ABC
(2)2π22×π22
2,
∴阴影部分的面积为2.
故答案为:A.
【点评】本题考查扇形面积的计算、含30度角的直角三角形、勾股定理,掌握特殊角的三角函数、扇形和三角形面积计算公式是解题的关键.
5.(2024 广水市模拟)如图,在Rt△ABC中,∠ABC=40°,AB=6,斜边AB是半圆O的直径,点D是半圆上的一个动点,连接CD与AB交于点E,若BE=BC时,弧BD的长为( )
A. B. C. D.
【考点】弧长的计算;圆周角定理.
【专题】圆的有关概念及性质;与圆有关的计算;运算能力.
【答案】B
【分析】根据BE=BC求出∠BOD,利用弧长公式求解即可.
【解答】解:如图1,当BE=BC时,
∵BE=BC,∠ABC=40°,
∴∠BCE=∠BEC(180°﹣40°)=70°,
∴∠BOD=2∠BCE=140°,
∴弧BD的长π.
故选:B.
【点评】本题考查弧长公式,圆周角定理,等腰三角形的性质,三角形内角和定理等知识,解题的关键是根据圆周角定理求出∠BOD=140°.
二.填空题(共5小题)
6.(2024秋 青秀区校级期中)小李同学在数学综合实践活动中,用一块扇形材料制作了一个圆锥模型(如图所示),经过小黄同学测量得圆锥底面直径为12cm,圆锥的高为8cm,则根据测量数据推算,该圆锥模型的侧面积为 60π cm2.
【考点】圆锥的计算.
【专题】展开与折叠;运算能力.
【答案】60π.
【分析】先利用勾股定理计算出圆锥的母线长,再根据扇形的面积公式计算圆锥的侧面积.
【解答】解:根据题意,圆锥的母线长10(cm),
所以该圆锥的侧面积12π×10=60π(cm2).
故答案为:60π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
7.(2024 金湖县一模)已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是 15π .
【考点】圆锥的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【解答】解:圆锥的侧面积 2π 3 5=15π.
故答案为15π.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
8.(2024秋 南京期中)如图,在△ABC中,AB=AC=6,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则扇形ODE的面积为 π .
【考点】扇形面积的计算;等腰三角形的性质.
【专题】与圆有关的计算;运算能力.
【答案】.
【分析】连接OE,OD,由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO,由OE=OA,∠OEA=∠BAC=50°,因此∠EOD=∠BAC=50°,由扇形的面积公式计算即可.
【解答】解:∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO,
∵OE=OA,
∴∠OEA=∠BAC=50°,
∴∠EOD=∠BAC=50°,
∵ODAB=3,
∴扇形ODE的面积为π.
故答案为:.
【点评】本题考查扇形面积的计算,等腰三角形的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
9.(2024秋 建邺区期中)用半径为5cm,圆心角为72°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥的高为 cm.
【考点】圆锥的计算;展开图折叠成几何体.
【专题】圆的有关概念及性质;应用意识.
【答案】.
【分析】根据题意,设圆锥的底面半径为r厘米,这个扇形的弧长等于圆锥的底面周长,根据公式表示出圆的周长和弧长,求出半径,再利用勾股定理,求出圆锥的高,据此解答.
【解答】解:设圆锥的底面半径为r厘米.
,
,
r=1,
圆锥的高为(厘米).
答:这个圆锥的高为cm.
故答案为:.
【点评】本题考查了圆锥的计算、展开图折叠成几何体,解决本题的关键是先求出圆锥的底面半径.
10.(2024春 沛县校级期末)如图所示,分别以n边形的顶点为圆心,以2cm为半径画圆,当n=2024时,则图中阴影部分的面积之和为 4π cm2.(注:结果用含π的式子表示)
【考点】扇形面积的计算.
【专题】圆的有关概念及性质;运算能力.
【答案】4π.
【分析】由题意得到各顶点的扇形圆心角之和即为n边形外角和,利用扇形面积公式计算即可求出阴影部分面积.
【解答】解:∵n边形的外角和为360°,半径为2cm,
∴S阴影4πcm2,
故答案为:4π.
【点评】此题考查了扇形面积的计算,以及多边形的内角和与外角和,熟练掌握扇形面积公式是解本题的关键.
三.解答题(共5小题)
11.(2024秋 溧阳市期中)如图,扇形AOB中,∠AOB=90°,点P是AB上一点,APBP.
(1)求扇形AOB的面积;
(2)过点P作PQ⊥AB交弧AB于点Q,求PQ的长.
【考点】扇形面积的计算.
【专题】与圆有关的计算;运算能力.
【答案】(1)9π;
(2).
【分析】(1)依题意得AB,OA=OB,∠AOB=90°,则△OAB是等腰直角三角形,再由勾股定理求出OA=6,进而可得扇形AOB的面积;
(2)过O作OC⊥AB于C,OD⊥PQ交QP的延长线于D,QD交OA于E,证明四边形OCPD为矩形,再根据△OAB是等腰直角三角形得AC=BC=OC,OQ=OA=6,则OD=PC,PD=OC,然后由勾股定理求出DQ,进而可得PQ的长.
【解答】解:(1)∵APBP,
∴AP,BP,
∴AB=AP+BP,
∵OA=OB,∠AOB=90°,
∴△OAB是等腰直角三角形,
由勾股定理得:AB,
∴,
∴OA=6,
∴扇形AOB的面积为:9π;
(2)过点O作OC⊥AB于C,作OD⊥PQ交QP的延长线于D,QD交OA于点E,连接OQ,如图所示:
∵PQ⊥AB,
∴四边形OCPD为矩形,
∴OC=DP,OD=PC,
由(1)知:△OAB是等腰直角三角形,且OA=OB=6,AB,AP,
∴AC=BC=OCAB,OQ=OA=6,
∴OD=PC=AC﹣AP,PD=OC,
在Rt△ODQ中,由勾股定理得:DQ,
∴PQ=DQ﹣PD.
【点评】此题主要考查了扇形面积,熟练掌握扇形的面积公式是解决问题的关键.
12.(2024 包河区校级三模)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若,AE=2,求阴影部分面积.
【考点】扇形面积的计算;勾股定理;垂径定理;圆周角定理.
【专题】圆的有关概念及性质;推理能力.
【答案】见试题解答内容
【分析】(1)根据等腰三角形性质求出∠BCO=∠B,根据圆周角定理得出∠B=∠D,再求出答案即可;
(2)根据垂径定理求出CE=2,再根据勾股定理求出OC,进一步即可求得OE,利用直角三角函数求得∠AOC=60°,然后根据S阴影=S扇形AOC﹣S△COE求解即可.
【解答】(1)证明:∵OC=OB,
∴∠BCO=∠B,
∵∠B=∠D,
∴∠BCO=∠D;
(2)解:∵AB 是⊙O的直径,CD⊥AB于点E,
∴,
∵,
∴,
在Rt△OCE 中,OC2=CE2+OE2,
∴,
解得:r=4(负数舍去),
∴OC=OA=4,
∴OE=4﹣2=2,
∴tan,
∴∠AOC=60°,
∴S阴影=S扇形AOC﹣S△COEπ﹣2.
【点评】本题考查了扇形的面积,垂径定理,勾股定理,等腰三角形的性质,圆周角定理等知识点,熟练掌握性质定理,明确S阴影=S扇形AOC﹣S△COE是解此题的关键.
13.(2024秋 南京期中)如图,在正方形网格中建立平面直角坐标系,一条圆弧经过格点A(0,4),B(﹣4,4),C(﹣6,2),该圆弧所在圆的圆心为P.
(1)点P的坐标为 (﹣2,0) ,⊙P的半径为 2 .
(2)若扇形PAC是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为 .
【考点】圆锥的计算;坐标与图形性质;垂径定理.
【专题】等腰三角形与直角三角形;圆的有关概念及性质;与圆有关的计算;运算能力;推理能力.
【答案】(1)(﹣2,0),2;
(2).
【分析】(1)根据垂径定理以及勾股定理进行计算即可;
(2)求出扇形PAC的圆心角度数,进而求出弧AC的长,再根据圆锥侧面展开图的特征进行计算即可.
【解答】解:(1)如图,依据网格,作AB,BC的中垂线相交于点P,点P的坐标为(﹣2,0),
PA2,
即⊙P的半径为2,
故答案为:(﹣2,0),2;
(2)如图,易证△AOP≌△PDC(SAS),
∴∠OAP=∠DPC,
∴∠OAP+∠OPA=90°,
∴∠DPC+∠OPA=90°,
∴∠APC=180°﹣90°=90°,
∴的长为π,
设圆锥的底面半径为r,则2πrπ,
解得r,
故答案为:.
【点评】本题考查垂径定理、勾股定理,圆锥的计算,掌握垂径定理、勾股定理以及弧长、圆周长的计算方法是正确解答的关键.
14.(2024秋 蓬江区校级期中)如图,在△ABC中,∠ACB=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求∠ACD的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积.
【考点】扇形面积的计算;直角三角形斜边上的中线;圆周角定理.
【专题】等腰三角形与直角三角形;与圆有关的计算;推理能力.
【答案】(1)56°;
(2).
【分析】(1)利用直角三角形的两锐角互余计算出∠BAC=62°,然后根据等腰三角形的性质及三角形内角和定理计算出∠ACD的度数;
(2)利用斜边上的中线性质得到CD=AD=BDAB=1,再判断△ACD为等边三角形,则∠ACD=60°,利用扇形的面积公式,根据阴影部分的面积=S扇形ACD进行计算.
【解答】解:(1)∵∠ACB=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵CA=CD,
∴∠CDA=∠CAD=62°,
∴∠ACD=180°﹣62°﹣62°=56°;
(2)∵D是AB的中点,∠ACB=90°,
∴CD=AD=BDAB=1,
∵CD=CA,
∴△ACD为等边三角形,
∴∠ACD=60°,
∴阴影部分的面积=S扇形ACD.
【点评】本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形πR2或S扇形lR(其中l为扇形的弧长).
15.(2024秋 滨湖区期末)如图1,已知四边形ABCD内接于⊙O,AC为⊙O的直径,AD=DB,AC与BD交于点E,且AE=BC.
(1)求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转35°得到△FGC,点A经过的路径为弧AF,若AC=4,求图中阴影部分的面积.
【考点】扇形面积的计算;旋转的性质;全等三角形的判定与性质.
【专题】与圆有关的计算.
【答案】见试题解答内容
【分析】(1)证明△ADE≌△BDC(SAS),推出∠ADE=∠BDC,推出即可解决问题.
(2)证明S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF即可解决问题.
【解答】(1)证明:∵AD=BD,∠DAE=∠DBC,AE=BC,
∴△ADE≌△BDC(SAS),
∴∠ADE=∠BDC,
∴.
∴AB=BC.
(2)解:S阴=S扇形CAF+S△CFG﹣S△ABC=S扇形CAF.
【点评】本题考查扇形的面积公式,全等三角形的判定和性质,等腰三角形的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
