广东省深圳市2024-2025学年高一下学期期末调研测试数学试题(图片版,含答案)
文档属性
| 名称 | 广东省深圳市2024-2025学年高一下学期期末调研测试数学试题(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 00:00:00 | ||
图片预览




文档简介
2025 年深圳市普通高中高一年级调研考试
数学试题参考答案及评分标准
一、选择题:本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题
目要求。
题号 1 2 3 4 5 6 7 8
答案 B B D D C A A C
命题说明:
1.题源:2023年北京卷第 2题.
2.题源:2023年全国新课标Ⅰ卷第 1题.
3.题源:人教 A版必修第一册 184页练习第 2题.
4.题源:人教 A版必修第二册 23页第 11题.
5.题源:2011年全国新课标Ⅰ卷(文科)第 3题.
6.题源:人教 A版必修第二册 163页第 9题.
7.题源:2023年全国新课标Ⅰ卷第 4题.
8.题源:人教 A版必修第二册 266页第 2题.
二、选择题:本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 6分,部分选对的得部分分,有选错的得 0分。
题号 9 10 11
答案 AC ABD ABD
命题说明:
9. 题源:2016年全国新课标Ⅰ卷(文科)第 8题.
10.题源:人教 A版必修第一册 229页第 12题(3).
11.题源:2009年全国新课标卷第 8题.
三、填空题:本题共 4小题,每小题 5分,共 20分。
19π
12. 1 ; 13. ; 14. 3 ;
3
命题说明:
数学试题参考答案及评分标准第 1 页 共 9 页
12.题源:人教 A版必修第二册 60页第 8题.
13.题源:2023年新课标全国Ⅰ卷 14题.
14.题源:原创.
a 2a a 2 a 2
解法 1 由于 bsin B csin B 1 ac sin B 1 bc sin A ,
2 2
由余弦定理: a2 b2 c2 2bc cosA,
2
y b c
2 2bc cosA 5 4cosA
则 1 y 0bc sin A sin A ,其中 ,
2
4
则 5 ysin A 4cos A y 2 16 sin(A ) ,其中 tan y,
由于 5 y2 16 ,则 y 3,此时 tan 4 3 , tan A ;
3 4
解法 2 过 A作 AH BC,设 AH x,则
BH 4b2 x2 ,CH b2 x2 ,
a 4b2 x2 b2 x2
则 2( 4 (
b )2 1 (b )2 1)
bsin B b x x x
,
2b
t b令 ,
x y 4t
2 1 t 2 1,则 y t 2 1 4t 2 1,
则 y2 3t 2 2y t 2 1,则 y4 9t4 6t2 y2 4y2 (t2 1),
9
则 9t4 10y2t2 (y4 4y2 ) 0, 100y4 36y2 (y2 4) 0 2,则 y ,
4
9
y2 9 a当 10 2时, t 2 4 5 b 符合,从而 的最小值为3;4 18 4 x2 bsin B
四、解答题:本题共 5小题,共 77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
2
已知函数 f (x) a x 为奇函数.2 1
(1)求 a的值;
2
(2)若 f (x) ,求 x的取值范围.
3
数学试题参考答案及评分标准第 2 页 共 9 页
【命题说明】由人教 A版必修第一册 161页第 12题改编.
【参考答案】
(1)因为 f (x)为定义域为R 上的奇函数,
所以 f (0) a 1 0 , a 1,
x
当 a 1时, f (x) 2 1 x ,2 1
f ( x) 2
x 1 1 2x
x f (x),2 1 1 2x
所以当 a 1时, f (x)为R 上的奇函数;
x
2 f (x) 2 1 2( )由 x
2x
,且 2 1 0,
1 3
解得 2x 5,
即 x log2 5,
所以 x的取值范围为 ( , log2 5);
16.(15分)
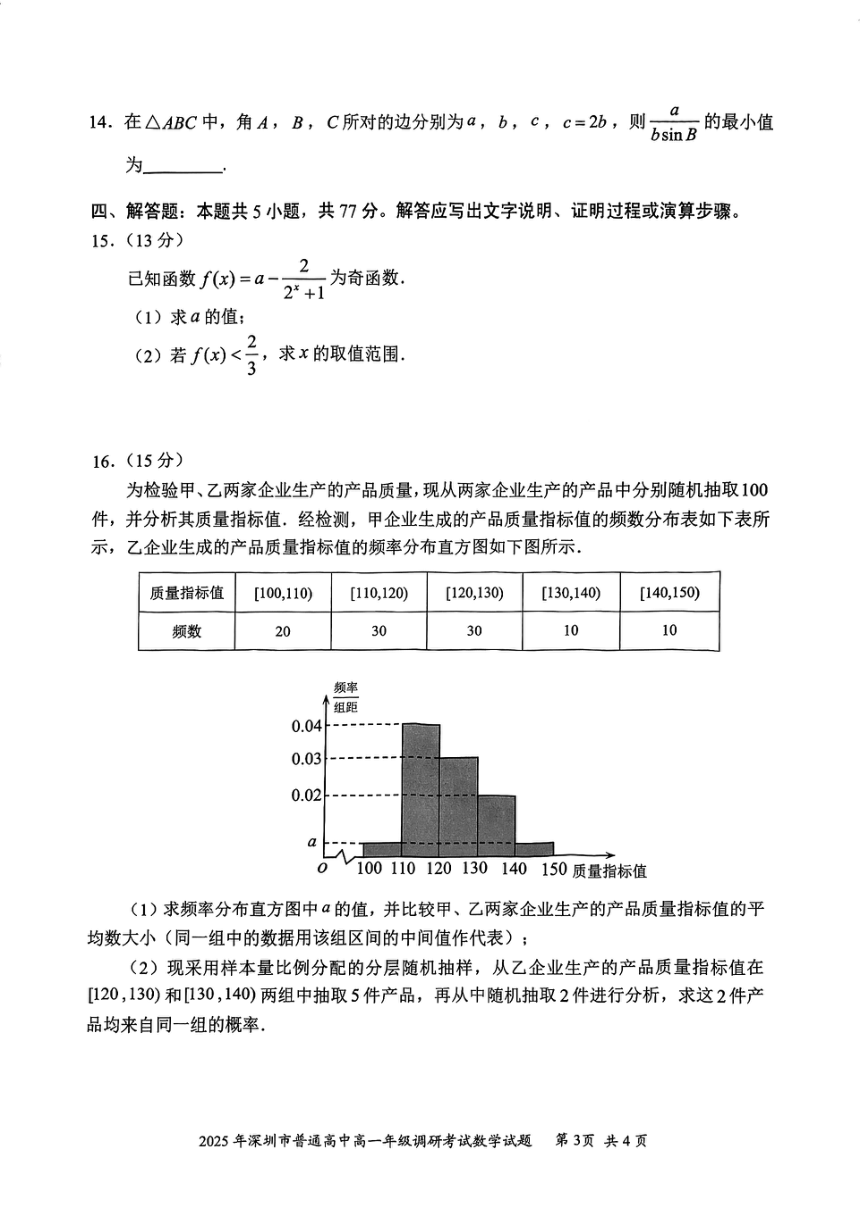
为检验甲、乙两家企业生产的产品质量,现从两家企业生产的产品中分别随机抽取100件,并
分析其质量指标值.经检测,甲企业生成的产品质量指标值的频数分布表如下表所示,乙企业生成
的产品质量指标值的频率分布直方图如下图所示.
质量指标值 [100,110) [110,120) [120,130) [130,140) [140,150)
频数 20 30 30 10 10
频率
组距
0.04
0.03
0.02
a
o 100 110 120 130 140 150 质量指标值
(1)求频率分布直方图中 a的值,并比较甲、乙两家企业生产的产品质量指标值的平均数大小
(同一组中的数据用该组区间的中间值作代表);
(2)现采用样本量比例分配的分层随机抽样,从乙企业生产的产品质量指标值在[120 ,130)和
[130 ,140)两组中抽取 5件产品,再从中随机抽取 2件进行分析,求这 2件产品均来自同一组的概率.
【命题说明】由 2014年重庆卷(文科)第 17题和 2014年新课标Ⅰ卷第 18题改编.
数学试题参考答案及评分标准第 3 页 共 9 页
【参考答案】
(1)由频率分布直方图中数据可知:10 (a 0.04 0.03 0.02 a) 1 ,解得 a 0.005 .
企业甲所生产的产品的质量指标值的平均数为:
x甲 105 0.2 115 0.3 125 0.3 135 0.1 145 0.1 121 ,
企业乙所生产的产品的质量指标值的平均数为:
x乙 105 0.05 115 0.4 125 0.3 135 0.2 145 0.05 123 ,
因为 x甲 x乙,所以乙企业生产的产品质量指标值的平均数更大;
(2)由频数分布表可知,乙企业生产的产品其质量指标值在区间 [100,110) 的有 20台,在区间
[110,120)的有30台,
由分层抽样可知,所抽取的 5台产品中, [100,110)组有 2台, [110,120)组有 3台,
记 [100,110)组的 2台产品为 A,B, [110,120)组的 3台产品为 a,b,c,
则从 5台产品中随机抽取 2台的所有可能结果为:
(A , B) , (A , a) , (A , b) , (A , c), (B , a) , (B , b) , (B , c) , (a , b) , (a , c) , (b , c),共10种情况,
其中这 2件产品均来自同一组包含的所有结果为: (A , B) , (a , b) , (a , c) , (b , c),共 4种情况,
4 2
故抽取的 2台充电宝均为优秀产品的概率 P .
10 5
17.(15分)
如图,在三棱柱ABC A1B1C1中,平面 ABC 平面BCC1B1, B1BC 60 ,点M 为BC中点.
(1)证明: A1B //平面 AMC1;
(2)若 AB AC BC 2CC1,求直线 AC与平面 AMC1所成角的正弦值.
A1 A
【命题说明】原创.
B1 B
【参考答案】
M
(1)连接 A1C,交 AC1于 D,连接DM . C1 C
因为四边形 ACC1A1为平行四边形,点D为对角线的交点,
所以 D为 A1C的中点,
因为点M 为 BC的中点,所以MD∥A1B,
数学试题参考答案及评分标准第 4 页 共 9 页
因为MD 平面 AMC1, A1B 平面 AMC1,
所以 A1B∥平面 AMC1.
(2)解法一:过C作CH C1M ,交C1M 于点 H ,连接 AH .
因为 AB AC,点M 为 BC中点,所以 AM BC ,
又因为平面 BCC1B1 平面 ABC,平面 BCC1B1 I平面 ABC BC, AM 平面 ABC,
所以 AM 平面 BCC1B1, A1 A
因为CH 平面 BCC1B1,所以 AM CH ,
又因为CH C1M , AM IC1M M , AM ,C1M 平面 AC1M ,
D
所以CH 平面 AC1M ,
B1 B
所以 CAH 为直线 AC 与平面 AMC1所成角. H M
C1 C
设 AB AC BC 2CC
1
1 2a ,则CM BC CC1 a,2
所以△CC1M 为等腰三角形,
又因为在平行四边形 BCC1B1中, B1BC 60 ,所以 BCC1 120 ,
CC M 30 CH 1 a所以 1 ,于是 CC ,2 1 2
a
所以 sin CAH CH 1 2 ,
AC 2a 4
1
即直线 AC与平面 AMC1所成角的正弦值为 .4
解法二:因为平面 BCC1B1 平面 ABC,平面 BCC1B1 I平面 ABC BC, AM 平面 ABC,
所以 AM 平面 BCC1B1.
设 AB AC BC 2CC 2a CM
1
1 ,则 BC a , AM AC 2 CM 22 3a
.
因为在平行四边形 BCC1B1中, B1BC 60 ,所以 BCC1 120 ,
1
所以 S△CC M CM CC1 sin C1CM
1
a a sin120 3 a 2 .
1 2 2 4
又因为 AM 平面 BCC1B1,C1M 平面 BCC1B1,所以 AM C1M ,
数学试题参考答案及评分标准第 5 页 共 9 页
在△CC1M 中,由余弦定理得C1M CM
2 CC 21 2 CM CC1 cos120 3a ,
1
所以 S△AC M AM C
1
1M 3a
3
3a a 2,
1 2 2 2
设点C到平面 AMC1的距离为 h,
1 1 A1 A
由于VA CC1M VC AC1M ,所以 AM S△CC M h S3 1 3 △AC
,
1M
3 2
AM S 3a a
h △CC1M 4 a所以 ,
S△AC M 3 a2 21
2
设直线 AC与平面 AMC1所成角为 , B1
B
M
a
h 1 C则 1 Csin 2 ,
AC 2a 4
1
即直线 AC与平面 AMC1所成角的正弦值为 .4
18.(17分)
在△ABC中, BC, AC边上的两条中线 AM , BN 相交于点 P,若 AB : AM : AC 6 : 7 :10.
uuur uuur uuur uuur
(1)用 AB, AC表示 AM , BN ;
(2)求 BAC;
uuur uuur
(3)若 AM BN 2,求四边形 PMCN的面积.
【命题说明】由人教 A版必修第二册 53页第 12题改编.
【参考答案】
uuur 1 uuur uuur uuur uur uuur uuur 1 uuur
(1) AM (AB AC), BN BA AN AB AC ;
2 2
(2)不妨设 AB 6m (m 0 ),则 AC 10m, AM 7m,
uuur uuur uuur uuur2 uuur2 uuur2 uuur uuur
由于 2AM AB AC,可得 4AM AB AC 2AB AC,
uuur uuur uuur 2 uuur 2 uuur 2
所以 AB AC
1 1
2AM AB AC 30m 2 ,
2 2
uuur uuur uuur uuur
又 AB AC | AB || AC | cos BAC 60m 2 cos BAC ,
所以 cos
1
BAC ,
2
数学试题参考答案及评分标准第 6 页 共 9 页
因为 BAC (0 , π)
π
,所以 BAC ;
3
uuur uuur 1 uuur 1 uuur uuur 1 uuur 1 uuur 2 1 uuur uuur uuur 2
(3)由(1)可知 AM BN ( AB AC ) ( AB AC ) AB AB AC
1 1
AC m 2 2 ,
2 2 2 2 4 4 2
则m 2,故 AB 12, AC 20,
如图,连接MN ,由题意得MN 为△ABC的中位线, A
所以△CMN∽△CBA,△PMN∽△PAB,
N
AB AP BP
所以 2 PMN PM PN ,
故 S
1
△CMN S4 △ABC
, B M C
S 1 S 1 1 1 1△PMN 3 △AMN
S
3 △CMN
S
3 4 △ABC
S
12 △ABC
,
所以 S
1 1 1
四边形PMCN S△PMN S△CMN S△ABC AB AC sin BAC 20 3.3 3 2
19.(17分)
已知函数 f (x) sin 2 x 2acos x a2 b.
1
(1)当 a 时, f (x) 0,求b的取值范围;
2
(2)求 f (x)的值域;
x [0 , π(3)当 ]时, | f (x) | 2,求b a的最大值.
2
【命题说明】原创.
【参考答案】
1 2
1 2
( ) f (x) sin x cos x b cos x cos x
3
b
4 4
(cos x 1 )2 1 b,
2
1
所以当 cos x 时, f (x)min 1 b ,2
因为 f (x) 0,
则 f (x)min 1 b 0,即 b 1,
所以b的取值范围为 ( , 1];
(2) t cos x [ 1 ,1],则令 g(t) t 2 2at a2 b 1 .
数学试题参考答案及评分标准第 7 页 共 9 页
①若 a 1,则 f (t)在 [ 1,1]上单调递减,
Q g( 1) a2 2a b, g(1) a2 2a b,
g(t) [ a2 2a b , a2 2a b] ;
②若 1 a 0,则 f (t)在 [ 1,a]上单调递增,在[a,1]上单调递减,
Q g(a) 1 b,且 g(1) g( 1),
g(t) [ a2 2a b , 1 b];
③若 0 a 1,则 f (t)在[ 1,a]上单调递增,在[a,1]上单调递减,
Q g(a) 1 b,且 g( 1) g(1),
则 g(t) [ a2 2a b , 1 b];
④若 a 1,则 f (t)在[ 1,1]上单调递增,
Q g( 1) a2 2a b, g(1) a2 2a b,
则 g(t) [ a2 2a b , a2 2a b] ;
综上所述,①当 a 1时, f (x)的值域为 [ a2 2a b , a2 2a b] ;
②当 1 a 0时, f (x)的值域为 [ a2 2a b , 1 b];
③当 0 a 1时, f (x)的值域为 [ a2 2a b , 1 b];
④当 a 1时, f (x)的值域为 [ a2 2a b , a2 2a b] .
3 2 g(0) 2 a2 1 b a2 3
(3)①当 a 0时,由(2)知:
2 2 g(1) 2
,进一步整理得 ,
2 a 2a 2 b a2 2a 2
Q 3 a 0,
2
a2 2a 2 a2 1, a2 2a 2 a2 3 .
因此可得 1 a2 b a2 2a 2 .
所以 b a a2 a 2 2;
2 2
②当1 a 5
2 g(0) 2 a 1 b a 3
时,由(2)知: ,进一步整理得
2 2 g(1) 2
a2
,
2a 2 b a2 2a 2
Q1 a 5 ,
2
a2 2a 2 a2 1, a2 2a 2 a2 3 .
数学试题参考答案及评分标准第 8 页 共 9 页
因此可得 a2 2a 2 b 3 a2 ,
所以 b a a2 a 3 1;
1 2 g(a) 2
1 b 3
③当 0 a 时,则
2 2 g(1) 2
,进一步整理得 ,
a
2 2a 2 b a2 2a 2
Q 0 a 1 ,
2
a2 2a 2 1,且 a2 2a 2 3,
1 b a2 2a 2 ,
2 9
因此可得 b a a a 2 ;
4
1 2 g(a) 2 1 b 3
④当 a 1时,则
2 2 g(0) 2
,进一步整理得
a
2 1 b , a2 3
Q 1 a 1,
2 a
2 1 1,且 a2 3 3,
1 b a2 3,
2
因此可得 b a a a 3 9 ;
4
1 11 9
综上所述,当 a ,b 时, b a取到最大值,最大值为 .
2 4 4
数学试题参考答案及评分标准第 9 页 共 9 页
数学试题参考答案及评分标准
一、选择题:本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题
目要求。
题号 1 2 3 4 5 6 7 8
答案 B B D D C A A C
命题说明:
1.题源:2023年北京卷第 2题.
2.题源:2023年全国新课标Ⅰ卷第 1题.
3.题源:人教 A版必修第一册 184页练习第 2题.
4.题源:人教 A版必修第二册 23页第 11题.
5.题源:2011年全国新课标Ⅰ卷(文科)第 3题.
6.题源:人教 A版必修第二册 163页第 9题.
7.题源:2023年全国新课标Ⅰ卷第 4题.
8.题源:人教 A版必修第二册 266页第 2题.
二、选择题:本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 6分,部分选对的得部分分,有选错的得 0分。
题号 9 10 11
答案 AC ABD ABD
命题说明:
9. 题源:2016年全国新课标Ⅰ卷(文科)第 8题.
10.题源:人教 A版必修第一册 229页第 12题(3).
11.题源:2009年全国新课标卷第 8题.
三、填空题:本题共 4小题,每小题 5分,共 20分。
19π
12. 1 ; 13. ; 14. 3 ;
3
命题说明:
数学试题参考答案及评分标准第 1 页 共 9 页
12.题源:人教 A版必修第二册 60页第 8题.
13.题源:2023年新课标全国Ⅰ卷 14题.
14.题源:原创.
a 2a a 2 a 2
解法 1 由于 bsin B csin B 1 ac sin B 1 bc sin A ,
2 2
由余弦定理: a2 b2 c2 2bc cosA,
2
y b c
2 2bc cosA 5 4cosA
则 1 y 0bc sin A sin A ,其中 ,
2
4
则 5 ysin A 4cos A y 2 16 sin(A ) ,其中 tan y,
由于 5 y2 16 ,则 y 3,此时 tan 4 3 , tan A ;
3 4
解法 2 过 A作 AH BC,设 AH x,则
BH 4b2 x2 ,CH b2 x2 ,
a 4b2 x2 b2 x2
则 2( 4 (
b )2 1 (b )2 1)
bsin B b x x x
,
2b
t b令 ,
x y 4t
2 1 t 2 1,则 y t 2 1 4t 2 1,
则 y2 3t 2 2y t 2 1,则 y4 9t4 6t2 y2 4y2 (t2 1),
9
则 9t4 10y2t2 (y4 4y2 ) 0, 100y4 36y2 (y2 4) 0 2,则 y ,
4
9
y2 9 a当 10 2时, t 2 4 5 b 符合,从而 的最小值为3;4 18 4 x2 bsin B
四、解答题:本题共 5小题,共 77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)
2
已知函数 f (x) a x 为奇函数.2 1
(1)求 a的值;
2
(2)若 f (x) ,求 x的取值范围.
3
数学试题参考答案及评分标准第 2 页 共 9 页
【命题说明】由人教 A版必修第一册 161页第 12题改编.
【参考答案】
(1)因为 f (x)为定义域为R 上的奇函数,
所以 f (0) a 1 0 , a 1,
x
当 a 1时, f (x) 2 1 x ,2 1
f ( x) 2
x 1 1 2x
x f (x),2 1 1 2x
所以当 a 1时, f (x)为R 上的奇函数;
x
2 f (x) 2 1 2( )由 x
2x
,且 2 1 0,
1 3
解得 2x 5,
即 x log2 5,
所以 x的取值范围为 ( , log2 5);
16.(15分)
为检验甲、乙两家企业生产的产品质量,现从两家企业生产的产品中分别随机抽取100件,并
分析其质量指标值.经检测,甲企业生成的产品质量指标值的频数分布表如下表所示,乙企业生成
的产品质量指标值的频率分布直方图如下图所示.
质量指标值 [100,110) [110,120) [120,130) [130,140) [140,150)
频数 20 30 30 10 10
频率
组距
0.04
0.03
0.02
a
o 100 110 120 130 140 150 质量指标值
(1)求频率分布直方图中 a的值,并比较甲、乙两家企业生产的产品质量指标值的平均数大小
(同一组中的数据用该组区间的中间值作代表);
(2)现采用样本量比例分配的分层随机抽样,从乙企业生产的产品质量指标值在[120 ,130)和
[130 ,140)两组中抽取 5件产品,再从中随机抽取 2件进行分析,求这 2件产品均来自同一组的概率.
【命题说明】由 2014年重庆卷(文科)第 17题和 2014年新课标Ⅰ卷第 18题改编.
数学试题参考答案及评分标准第 3 页 共 9 页
【参考答案】
(1)由频率分布直方图中数据可知:10 (a 0.04 0.03 0.02 a) 1 ,解得 a 0.005 .
企业甲所生产的产品的质量指标值的平均数为:
x甲 105 0.2 115 0.3 125 0.3 135 0.1 145 0.1 121 ,
企业乙所生产的产品的质量指标值的平均数为:
x乙 105 0.05 115 0.4 125 0.3 135 0.2 145 0.05 123 ,
因为 x甲 x乙,所以乙企业生产的产品质量指标值的平均数更大;
(2)由频数分布表可知,乙企业生产的产品其质量指标值在区间 [100,110) 的有 20台,在区间
[110,120)的有30台,
由分层抽样可知,所抽取的 5台产品中, [100,110)组有 2台, [110,120)组有 3台,
记 [100,110)组的 2台产品为 A,B, [110,120)组的 3台产品为 a,b,c,
则从 5台产品中随机抽取 2台的所有可能结果为:
(A , B) , (A , a) , (A , b) , (A , c), (B , a) , (B , b) , (B , c) , (a , b) , (a , c) , (b , c),共10种情况,
其中这 2件产品均来自同一组包含的所有结果为: (A , B) , (a , b) , (a , c) , (b , c),共 4种情况,
4 2
故抽取的 2台充电宝均为优秀产品的概率 P .
10 5
17.(15分)
如图,在三棱柱ABC A1B1C1中,平面 ABC 平面BCC1B1, B1BC 60 ,点M 为BC中点.
(1)证明: A1B //平面 AMC1;
(2)若 AB AC BC 2CC1,求直线 AC与平面 AMC1所成角的正弦值.
A1 A
【命题说明】原创.
B1 B
【参考答案】
M
(1)连接 A1C,交 AC1于 D,连接DM . C1 C
因为四边形 ACC1A1为平行四边形,点D为对角线的交点,
所以 D为 A1C的中点,
因为点M 为 BC的中点,所以MD∥A1B,
数学试题参考答案及评分标准第 4 页 共 9 页
因为MD 平面 AMC1, A1B 平面 AMC1,
所以 A1B∥平面 AMC1.
(2)解法一:过C作CH C1M ,交C1M 于点 H ,连接 AH .
因为 AB AC,点M 为 BC中点,所以 AM BC ,
又因为平面 BCC1B1 平面 ABC,平面 BCC1B1 I平面 ABC BC, AM 平面 ABC,
所以 AM 平面 BCC1B1, A1 A
因为CH 平面 BCC1B1,所以 AM CH ,
又因为CH C1M , AM IC1M M , AM ,C1M 平面 AC1M ,
D
所以CH 平面 AC1M ,
B1 B
所以 CAH 为直线 AC 与平面 AMC1所成角. H M
C1 C
设 AB AC BC 2CC
1
1 2a ,则CM BC CC1 a,2
所以△CC1M 为等腰三角形,
又因为在平行四边形 BCC1B1中, B1BC 60 ,所以 BCC1 120 ,
CC M 30 CH 1 a所以 1 ,于是 CC ,2 1 2
a
所以 sin CAH CH 1 2 ,
AC 2a 4
1
即直线 AC与平面 AMC1所成角的正弦值为 .4
解法二:因为平面 BCC1B1 平面 ABC,平面 BCC1B1 I平面 ABC BC, AM 平面 ABC,
所以 AM 平面 BCC1B1.
设 AB AC BC 2CC 2a CM
1
1 ,则 BC a , AM AC 2 CM 22 3a
.
因为在平行四边形 BCC1B1中, B1BC 60 ,所以 BCC1 120 ,
1
所以 S△CC M CM CC1 sin C1CM
1
a a sin120 3 a 2 .
1 2 2 4
又因为 AM 平面 BCC1B1,C1M 平面 BCC1B1,所以 AM C1M ,
数学试题参考答案及评分标准第 5 页 共 9 页
在△CC1M 中,由余弦定理得C1M CM
2 CC 21 2 CM CC1 cos120 3a ,
1
所以 S△AC M AM C
1
1M 3a
3
3a a 2,
1 2 2 2
设点C到平面 AMC1的距离为 h,
1 1 A1 A
由于VA CC1M VC AC1M ,所以 AM S△CC M h S3 1 3 △AC
,
1M
3 2
AM S 3a a
h △CC1M 4 a所以 ,
S△AC M 3 a2 21
2
设直线 AC与平面 AMC1所成角为 , B1
B
M
a
h 1 C则 1 Csin 2 ,
AC 2a 4
1
即直线 AC与平面 AMC1所成角的正弦值为 .4
18.(17分)
在△ABC中, BC, AC边上的两条中线 AM , BN 相交于点 P,若 AB : AM : AC 6 : 7 :10.
uuur uuur uuur uuur
(1)用 AB, AC表示 AM , BN ;
(2)求 BAC;
uuur uuur
(3)若 AM BN 2,求四边形 PMCN的面积.
【命题说明】由人教 A版必修第二册 53页第 12题改编.
【参考答案】
uuur 1 uuur uuur uuur uur uuur uuur 1 uuur
(1) AM (AB AC), BN BA AN AB AC ;
2 2
(2)不妨设 AB 6m (m 0 ),则 AC 10m, AM 7m,
uuur uuur uuur uuur2 uuur2 uuur2 uuur uuur
由于 2AM AB AC,可得 4AM AB AC 2AB AC,
uuur uuur uuur 2 uuur 2 uuur 2
所以 AB AC
1 1
2AM AB AC 30m 2 ,
2 2
uuur uuur uuur uuur
又 AB AC | AB || AC | cos BAC 60m 2 cos BAC ,
所以 cos
1
BAC ,
2
数学试题参考答案及评分标准第 6 页 共 9 页
因为 BAC (0 , π)
π
,所以 BAC ;
3
uuur uuur 1 uuur 1 uuur uuur 1 uuur 1 uuur 2 1 uuur uuur uuur 2
(3)由(1)可知 AM BN ( AB AC ) ( AB AC ) AB AB AC
1 1
AC m 2 2 ,
2 2 2 2 4 4 2
则m 2,故 AB 12, AC 20,
如图,连接MN ,由题意得MN 为△ABC的中位线, A
所以△CMN∽△CBA,△PMN∽△PAB,
N
AB AP BP
所以 2 PMN PM PN ,
故 S
1
△CMN S4 △ABC
, B M C
S 1 S 1 1 1 1△PMN 3 △AMN
S
3 △CMN
S
3 4 △ABC
S
12 △ABC
,
所以 S
1 1 1
四边形PMCN S△PMN S△CMN S△ABC AB AC sin BAC 20 3.3 3 2
19.(17分)
已知函数 f (x) sin 2 x 2acos x a2 b.
1
(1)当 a 时, f (x) 0,求b的取值范围;
2
(2)求 f (x)的值域;
x [0 , π(3)当 ]时, | f (x) | 2,求b a的最大值.
2
【命题说明】原创.
【参考答案】
1 2
1 2
( ) f (x) sin x cos x b cos x cos x
3
b
4 4
(cos x 1 )2 1 b,
2
1
所以当 cos x 时, f (x)min 1 b ,2
因为 f (x) 0,
则 f (x)min 1 b 0,即 b 1,
所以b的取值范围为 ( , 1];
(2) t cos x [ 1 ,1],则令 g(t) t 2 2at a2 b 1 .
数学试题参考答案及评分标准第 7 页 共 9 页
①若 a 1,则 f (t)在 [ 1,1]上单调递减,
Q g( 1) a2 2a b, g(1) a2 2a b,
g(t) [ a2 2a b , a2 2a b] ;
②若 1 a 0,则 f (t)在 [ 1,a]上单调递增,在[a,1]上单调递减,
Q g(a) 1 b,且 g(1) g( 1),
g(t) [ a2 2a b , 1 b];
③若 0 a 1,则 f (t)在[ 1,a]上单调递增,在[a,1]上单调递减,
Q g(a) 1 b,且 g( 1) g(1),
则 g(t) [ a2 2a b , 1 b];
④若 a 1,则 f (t)在[ 1,1]上单调递增,
Q g( 1) a2 2a b, g(1) a2 2a b,
则 g(t) [ a2 2a b , a2 2a b] ;
综上所述,①当 a 1时, f (x)的值域为 [ a2 2a b , a2 2a b] ;
②当 1 a 0时, f (x)的值域为 [ a2 2a b , 1 b];
③当 0 a 1时, f (x)的值域为 [ a2 2a b , 1 b];
④当 a 1时, f (x)的值域为 [ a2 2a b , a2 2a b] .
3 2 g(0) 2 a2 1 b a2 3
(3)①当 a 0时,由(2)知:
2 2 g(1) 2
,进一步整理得 ,
2 a 2a 2 b a2 2a 2
Q 3 a 0,
2
a2 2a 2 a2 1, a2 2a 2 a2 3 .
因此可得 1 a2 b a2 2a 2 .
所以 b a a2 a 2 2;
2 2
②当1 a 5
2 g(0) 2 a 1 b a 3
时,由(2)知: ,进一步整理得
2 2 g(1) 2
a2
,
2a 2 b a2 2a 2
Q1 a 5 ,
2
a2 2a 2 a2 1, a2 2a 2 a2 3 .
数学试题参考答案及评分标准第 8 页 共 9 页
因此可得 a2 2a 2 b 3 a2 ,
所以 b a a2 a 3 1;
1 2 g(a) 2
1 b 3
③当 0 a 时,则
2 2 g(1) 2
,进一步整理得 ,
a
2 2a 2 b a2 2a 2
Q 0 a 1 ,
2
a2 2a 2 1,且 a2 2a 2 3,
1 b a2 2a 2 ,
2 9
因此可得 b a a a 2 ;
4
1 2 g(a) 2 1 b 3
④当 a 1时,则
2 2 g(0) 2
,进一步整理得
a
2 1 b , a2 3
Q 1 a 1,
2 a
2 1 1,且 a2 3 3,
1 b a2 3,
2
因此可得 b a a a 3 9 ;
4
1 11 9
综上所述,当 a ,b 时, b a取到最大值,最大值为 .
2 4 4
数学试题参考答案及评分标准第 9 页 共 9 页
同课章节目录
