18.4 整数指数幂 第1课时 整数指数幂 课件(共29张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 18.4 整数指数幂 第1课时 整数指数幂 课件(共29张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:25:26 | ||
图片预览







文档简介
(共29张PPT)
第18章 分式
18.4 整数指数幂
第1课时 整数指数幂
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
3世纪
丢番图
△
r
△
△
r
K
r
韦达(1540-1603)
16世纪
Aq
Acu
Aqq
aa,aaa,aaaa
哈里奥特(1560-1621)
17世纪
笛卡尔
1637年
a2,a3,a4
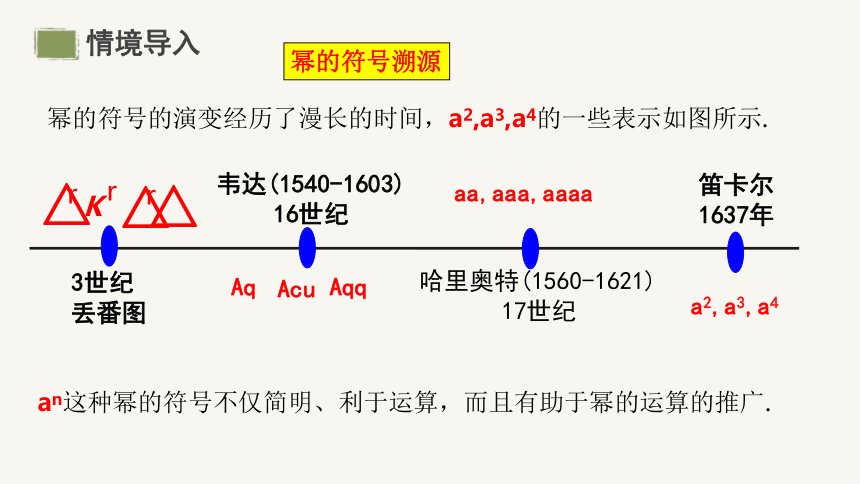
幂的符号溯源
幂的符号的演变经历了漫长的时间,a2,a3,a4的一些表示如图所示.
an这种幂的符号不仅简明、利于运算,而且有助于幂的运算的推广.
算一算,并分别说出每一小题所用的运算性质.
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
(1)a3·a4= ;
a7
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且m>n )
乘方:
(b≠0,n是正整数)
(6) = ;
(5) = ;
( )
新知初探
贰
新知初探
思考 你认为牛顿的这个设想合理吗?
也就是说,如果am中的m可以是负整数,那么负整数指数
幂am表示什么?
任务一 探究负整数指数幂的意义
活动1
1676年,牛顿提出了一个设想:“因为数学家将aa,aaa,aaaa,…写成a2,a3,a4,…,所以我将 ,…写成a-1,a-2,a-3,….”
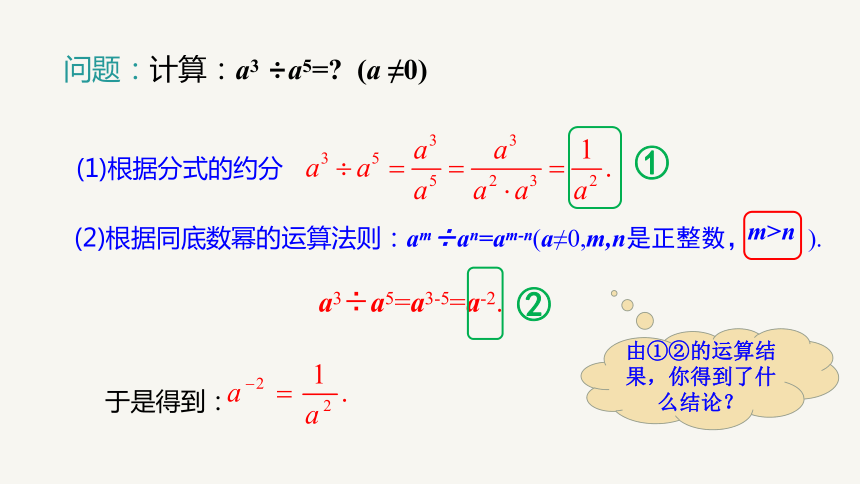
问题:计算:a3 ÷a5= (a ≠0)
(1)根据分式的约分
(2)根据同底数幂的运算法则:am÷an=am-n(a≠0,m,n是正整数, ).
于是得到:
a3÷a5=a3-5=a-2.
m>n
②
①
由①②的运算结果,你得到了什么结论?
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
这就是说,a-n (a≠0)是an的倒数.
即时测评
计算:
(1)3 = ;30 = ;3-2 = .
(2)(-3) = ;(-3)0 = ;(-3)-2 = .
(3)b0 = ; b-2 = (b≠0).
9
1
9
1
1
你能猜出:
当m分别是正整数、0 、负整数时,am分别表示什么意思吗?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
am=
am (m是正整数)
1 (m=0)
(m是负整数)
任务二 探究整数指数幂的性质
活动1
问题1 引入负整数指数和0指数后,am·an=am+n(m,n是正整数)这条性质能否推广到m,n是任意整数的情形
问题2 分别根据分式的约分和同底数幂的乘法法则计算:
(1)a3·a-5; (2)a-3·a-5; (3)a0·a-5.
解:(1)a3·a-5= =a-2=a3+(-5), 即 a3·a-5=a3+(-5) ;
(2)a-3·a-5= =a-8=a(-3)+(-5), 即 a-3·a-5=a(-3)+(-5) ;
(3)a0·a-5=1· = =a-5=a0+(-5), 即 a0·a-5=a(0)+(-5) .
am·an=am+n这条性质对于m,n是任意整数的情形仍然适用
归纳总结:
问题 3 类似地,你可以用负整数指数幂或 0 指数幂
对于其他正整数指数幂的运算性质进行试验,看看这些性质在整数范围内是否还适用?
①(am)n=amn(m,n是正整数);
②(ab)n=anbn(n是正整数);
③am÷an=am-n(a≠0,m,n是正整数,m>n);
④ (n是正整数).
解:①(a2)-3= =a2×(-3),即 (a2)-3=a2×(-3) .
②(ab)-2= =a-2b-2,即 (ab)-2=a-2b-2 .
③a-2÷a-3= =a=a(-2)-(-3),即 a-2÷a-3=a(-2)-(-3) .
④ ,即 .
随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
归纳总结:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) (m,n 是整数);
(5) (n 是整数).
归纳总结
范例应用
【例1】 计算:
解:
提示:计算结果一般需化为正整数幂的形式.
解:
即时测评
计算:
解:(1)原式=x2y-3·x-3y3
=x2-3·y-3+3
=x-1
=
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
所以
即商的乘方可以转化为积的乘方.
总结归纳
整数指数幂的运算性质归结为
(1)am·an=am+n ( m、n是整数) ;
(2)(am)n=amn ( m、n是整数) ;
(3)(ab)n=anbn ( n是整数).
当堂达标
叁
当堂达标
1.填空:(-3)2·(-3)-2=( );103×10-2=( );
a-2÷a3=( );a3÷a-4=( ).
2.计算:(1)0.1÷0.13
(2)(-5)2 024÷(-5)2 026
(3)100×10-1÷10-2
(4)x-2·x-3÷x2
1
10
a7
3.计算下列各式,并且把结果化为只含有正整数指数幂的形式.
(1)(a2b-3)-2·(a-2b3)2;
(2)a-2b2·(-2a2b-2)-2÷(a-4b2).
解:(1)原式=a-4b6·a-4b6=a-8b12= .
(3)原式=a-2b2· a-4b4·a4b-2= a-2b4= .
课堂小结
肆
课堂小结
整数
指数幂
负整数指数幂:当n是正整数时,a-n=
整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
第18章 分式
18.4 整数指数幂
第1课时 整数指数幂
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
3世纪
丢番图
△
r
△
△
r
K
r
韦达(1540-1603)
16世纪
Aq
Acu
Aqq
aa,aaa,aaaa
哈里奥特(1560-1621)
17世纪
笛卡尔
1637年
a2,a3,a4
幂的符号溯源
幂的符号的演变经历了漫长的时间,a2,a3,a4的一些表示如图所示.
an这种幂的符号不仅简明、利于运算,而且有助于幂的运算的推广.
算一算,并分别说出每一小题所用的运算性质.
(2) = ;
同底数幂的乘法:
(m,n是正整数)
幂的乘方:
(m,n是正整数)
(3) = ;
积的乘方:
(n是正整数)
(1)a3·a4= ;
a7
(4) = ;
同底数幂的除法:
(a≠0,m,n是正整数且m>n )
乘方:
(b≠0,n是正整数)
(6) = ;
(5) = ;
( )
新知初探
贰
新知初探
思考 你认为牛顿的这个设想合理吗?
也就是说,如果am中的m可以是负整数,那么负整数指数
幂am表示什么?
任务一 探究负整数指数幂的意义
活动1
1676年,牛顿提出了一个设想:“因为数学家将aa,aaa,aaaa,…写成a2,a3,a4,…,所以我将 ,…写成a-1,a-2,a-3,….”
问题:计算:a3 ÷a5= (a ≠0)
(1)根据分式的约分
(2)根据同底数幂的运算法则:am÷an=am-n(a≠0,m,n是正整数, ).
于是得到:
a3÷a5=a3-5=a-2.
m>n
②
①
由①②的运算结果,你得到了什么结论?
知识要点
负整数指数幂的意义
一般地,我们规定:当n是正整数时,
这就是说,a-n (a≠0)是an的倒数.
即时测评
计算:
(1)3 = ;30 = ;3-2 = .
(2)(-3) = ;(-3)0 = ;(-3)-2 = .
(3)b0 = ; b-2 = (b≠0).
9
1
9
1
1
你能猜出:
当m分别是正整数、0 、负整数时,am分别表示什么意思吗?
引入负整数指数幂后,指数的取值范围就扩大到全体整数。
am=
am (m是正整数)
1 (m=0)
(m是负整数)
任务二 探究整数指数幂的性质
活动1
问题1 引入负整数指数和0指数后,am·an=am+n(m,n是正整数)这条性质能否推广到m,n是任意整数的情形
问题2 分别根据分式的约分和同底数幂的乘法法则计算:
(1)a3·a-5; (2)a-3·a-5; (3)a0·a-5.
解:(1)a3·a-5= =a-2=a3+(-5), 即 a3·a-5=a3+(-5) ;
(2)a-3·a-5= =a-8=a(-3)+(-5), 即 a-3·a-5=a(-3)+(-5) ;
(3)a0·a-5=1· = =a-5=a0+(-5), 即 a0·a-5=a(0)+(-5) .
am·an=am+n这条性质对于m,n是任意整数的情形仍然适用
归纳总结:
问题 3 类似地,你可以用负整数指数幂或 0 指数幂
对于其他正整数指数幂的运算性质进行试验,看看这些性质在整数范围内是否还适用?
①(am)n=amn(m,n是正整数);
②(ab)n=anbn(n是正整数);
③am÷an=am-n(a≠0,m,n是正整数,m>n);
④ (n是正整数).
解:①(a2)-3= =a2×(-3),即 (a2)-3=a2×(-3) .
②(ab)-2= =a-2b-2,即 (ab)-2=a-2b-2 .
③a-2÷a-3= =a=a(-2)-(-3),即 a-2÷a-3=a(-2)-(-3) .
④ ,即 .
随着指数的取值范围由正整数推广到全体整数,前面提到的运算性质也推广到整数指数幂.
归纳总结:
(1) (m,n 是整数);
(2) (m,n 是整数);
(3) (n 是整数);
(4) (m,n 是整数);
(5) (n 是整数).
归纳总结
范例应用
【例1】 计算:
解:
提示:计算结果一般需化为正整数幂的形式.
解:
即时测评
计算:
解:(1)原式=x2y-3·x-3y3
=x2-3·y-3+3
=x-1
=
(1) 根据整数指数幂的运算性质,当m,n为整数时,
am ÷an=am-n
又am ·a-n=am-n,因此am ÷an=am ·a-n.
即同底数幂的除法可以转化为同底数幂的乘法.
(2) 特别地,
所以
即商的乘方可以转化为积的乘方.
总结归纳
整数指数幂的运算性质归结为
(1)am·an=am+n ( m、n是整数) ;
(2)(am)n=amn ( m、n是整数) ;
(3)(ab)n=anbn ( n是整数).
当堂达标
叁
当堂达标
1.填空:(-3)2·(-3)-2=( );103×10-2=( );
a-2÷a3=( );a3÷a-4=( ).
2.计算:(1)0.1÷0.13
(2)(-5)2 024÷(-5)2 026
(3)100×10-1÷10-2
(4)x-2·x-3÷x2
1
10
a7
3.计算下列各式,并且把结果化为只含有正整数指数幂的形式.
(1)(a2b-3)-2·(a-2b3)2;
(2)a-2b2·(-2a2b-2)-2÷(a-4b2).
解:(1)原式=a-4b6·a-4b6=a-8b12= .
(3)原式=a-2b2· a-4b4·a4b-2= a-2b4= .
课堂小结
肆
课堂小结
整数
指数幂
负整数指数幂:当n是正整数时,a-n=
整数指数幂的运算性质:
(1) am·an=am+n(m,n为整数,a≠0)
(2)(ab)m=ambm(m为整数,a≠0,b≠0)
(3)(am)n=amn(m,n为整数,a≠0)
课后作业
基础题:1.课后习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第7题
谢
谢
同课章节目录
