18.4 整数指数幂 第2课时 科学记数法 课件(共22张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 18.4 整数指数幂 第2课时 科学记数法 课件(共22张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:25:38 | ||
图片预览








文档简介
(共22张PPT)
第18章 分式
18.4 整数指数幂
第2课时 科学记数法
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
回顾科学记数法:
一些较大的数适合用科学记数法表示:
光速约为 3 108 m/s ,太阳半径约为 6.96 105 km.
科学记数法:绝对值大于10的数记成a×10n的形式.
1≤a<10,n是正整数.
(1)3 000 000 000= ;(2)246 000= .
想一想,用科学记数法表示下列各数:
3×109
2.46×105
思考 你能用科学记数法表示小于1的正数吗
新知初探
贰
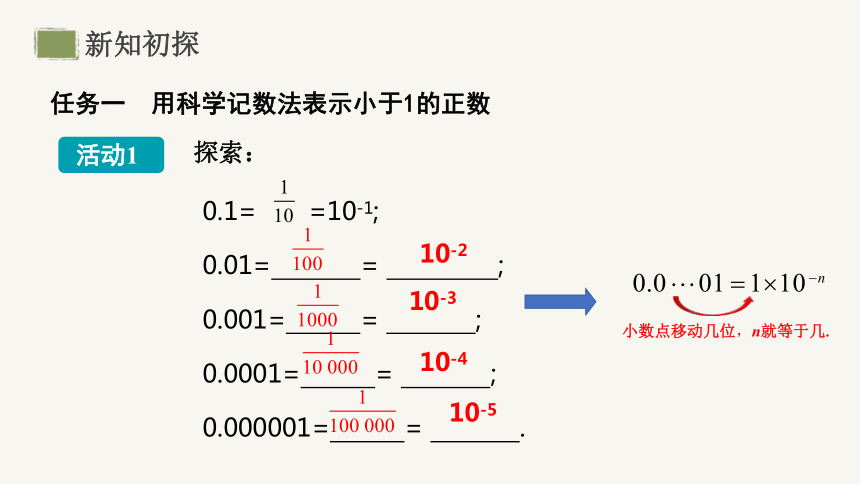
0.1= =10-1;
0.01= = ;
0.001= = ;
0.0001= = ;
0.000001= = .
新知初探
10-2
任务一 用科学记数法表示小于1的正数
活动1
探索:
10-3
10-4
10-5
0.0 01 1 10 n
小数点移动几位,n就等于几.
一般地,我们可以利用10的负整数次幂,用科学记数法表示一些小于1的正数,即将它们表示成a×10- n的形式,其中1≤a<10 , n是正整数.
范例应用
【例1】用科学记数法表示下列各数:
(1)0.0012= ;
(2)0.000 001 5= ;
(3)0.000 000 18= ;
(4)0.000 000 029= ;
(5)0.000 000 000 03= .
1.2×10-3
1.5×10-6
1.8×10-7
2.9×10-8
3×10-11
观察这些等式,你能发现10的指数与什么有关呢?
说出你发现的规律.
用科学记数法a×10-n表示小于1的正数时,n的取值为小数中第一个不为零的数字前面所有的零的个数.
归纳总结:
想一想 对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少
如果有m个0呢
-8
-m
【例2】 用小数表示下列各数:
(1)2×10-7; (2)3.14×10-5;
(3)7.08×10-3;(4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
自然科学和生活中经常用到的分(d)、厘(c)、毫(m)、微(μ)、纳(n)等国际单位制词头,其中微对应10-6,纳对应10-9,微米(μm)、纳米(nm)都是长度单位.
1μm=10-6m.1nm=10-9m.
纳米技术是一种高新技术,它可以在微观世界里直 接探索0.1至500nm范围内物质的特性,从而创造新材料.这项技术有重要应用.
学以致用
解:70μm=70×10-6m,2 nm=2×10-9m,20nm=20×10-9m.
【例3】碳纳米管是一种前沿纳米材料,有很多神奇
的特性.它是由呈六边形排列的碳原子构成的单层或多层的同轴圆管,其直径一般为2~20nm.通常一根头发丝的直径约为70μm,一根头发丝的直径大约是碳纳米管直径的多少倍 3
(70×10-6)÷(2×10-9)=3.5×104.
(70×10-6)÷(20×10-9)=3.5×103.
因此,一根头发丝的直径是的碳纳米管直径的3.5×103~3.5×104倍.
即时测评
计算:(结果用科学记数法表示)
(1)(6.5×10-9)×(5×10-4); (2)(2×10-5)÷(4×106)2.
(2)(2×10-5)÷(4×106)2
=(2×10-5)÷(16×1012)
=(2÷16)×(10-5÷1012)
=0.125×10-17
=1.25×10-18.
解:(1)(6.5×10-9)×(5×10-4)
=(6.5×5)×(10-9×10-4)
=32.5×10-13
=3.25×10-12.
当堂达标
叁
当堂达标
解:(1)0.003 009=3.009×10-3.
(2)-0.000 010 96=-1.096×10-5.
(3)0.000 329=3.29×10-4.
(4)0.000 000 004 05=4.05×10-9.
1. 用科学记数法表示下列各数.
(1)0.003 009; (2)-0.000 010 96;
(3)0.000 329; (4)0.000 000 004 05.
2.将以下用科学记数法表示的数写成小数的形式.
(1)3.02×10-5; (2)-2.14×10-7;
(3)5.7×10-6; (4)-1.07×10-8.
解:(1)3.02×10-5=3.02×0.00001=0.0000302.
(2)-2.14×10-7=-2.14×0.0000001=-0.000000214.
(3)5.7×10-6=5.7×0.000001=0.0000057.
(4)-1.07×10-8=-1.07×0.00000001=-0.0000000107.
3.计算:
(1)(-5.8×10-9)×(2×104); (2)(-4×10-2)2÷(0.5×10-3).
解:(1)(-5.8×10-9)×(2×104)
=-(5.8×2)×(10-9×104)
=-11.6×10-5
=-1.16×10-4.
(2)(-4×10-2)2÷(0.5×10-3)
=(-4)2×(10-2)2÷(0.5×10-3)
=(16×10-4)÷(0.5×10-3)
=(16÷0.5)×(10-4÷10-3)
=32×10-1=3.2.
4.为了打破国外芯片封锁,我国将加快完善集成
电路设计、制造、封测等产业链,开展EDA工具软件、半导体材料、高端芯片和专用芯片设计技术攻关,推进第三代半导体等重点项目建设.已知一块900mm2的芯片上能集成10亿个元件.
(1)每个这样的元件约占多少平方毫米
(2)每个这样的元件约占多少平方米
解:(1)10亿=10×108=1×109,
900÷(1×109)=9×10-7(mm2).
所以每个这样的元件约占9×10-7mm2.
(2)1m2=106mm2,9×10-7÷106=9×10-13(m2).
∴每个这样的元件约占9×10-13m2.
课堂小结
肆
课堂小结
用科学记数法表示绝对值小于1的正数
绝对值小于1的正数用科学记数法表示为a×10-n的形式,1≤a <10,n为原数第1个不为0的数字前面所有0的个数(包括小数点前面那个0).
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第18章 分式
18.4 整数指数幂
第2课时 科学记数法
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
回顾科学记数法:
一些较大的数适合用科学记数法表示:
光速约为 3 108 m/s ,太阳半径约为 6.96 105 km.
科学记数法:绝对值大于10的数记成a×10n的形式.
1≤a<10,n是正整数.
(1)3 000 000 000= ;(2)246 000= .
想一想,用科学记数法表示下列各数:
3×109
2.46×105
思考 你能用科学记数法表示小于1的正数吗
新知初探
贰
0.1= =10-1;
0.01= = ;
0.001= = ;
0.0001= = ;
0.000001= = .
新知初探
10-2
任务一 用科学记数法表示小于1的正数
活动1
探索:
10-3
10-4
10-5
0.0 01 1 10 n
小数点移动几位,n就等于几.
一般地,我们可以利用10的负整数次幂,用科学记数法表示一些小于1的正数,即将它们表示成a×10- n的形式,其中1≤a<10 , n是正整数.
范例应用
【例1】用科学记数法表示下列各数:
(1)0.0012= ;
(2)0.000 001 5= ;
(3)0.000 000 18= ;
(4)0.000 000 029= ;
(5)0.000 000 000 03= .
1.2×10-3
1.5×10-6
1.8×10-7
2.9×10-8
3×10-11
观察这些等式,你能发现10的指数与什么有关呢?
说出你发现的规律.
用科学记数法a×10-n表示小于1的正数时,n的取值为小数中第一个不为零的数字前面所有的零的个数.
归纳总结:
想一想 对于一个小于1的正小数,如果小数点后至第一个非0数字前有8个0,用科学记数法表示这个数时,10的指数是多少
如果有m个0呢
-8
-m
【例2】 用小数表示下列各数:
(1)2×10-7; (2)3.14×10-5;
(3)7.08×10-3;(4)2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1)2×10-7=0.0000002;
(2)3.14×10-5=0.0000314;
(3)7.08×10-3=0.00708;
(4)2.17×10-1=0.217.
自然科学和生活中经常用到的分(d)、厘(c)、毫(m)、微(μ)、纳(n)等国际单位制词头,其中微对应10-6,纳对应10-9,微米(μm)、纳米(nm)都是长度单位.
1μm=10-6m.1nm=10-9m.
纳米技术是一种高新技术,它可以在微观世界里直 接探索0.1至500nm范围内物质的特性,从而创造新材料.这项技术有重要应用.
学以致用
解:70μm=70×10-6m,2 nm=2×10-9m,20nm=20×10-9m.
【例3】碳纳米管是一种前沿纳米材料,有很多神奇
的特性.它是由呈六边形排列的碳原子构成的单层或多层的同轴圆管,其直径一般为2~20nm.通常一根头发丝的直径约为70μm,一根头发丝的直径大约是碳纳米管直径的多少倍 3
(70×10-6)÷(2×10-9)=3.5×104.
(70×10-6)÷(20×10-9)=3.5×103.
因此,一根头发丝的直径是的碳纳米管直径的3.5×103~3.5×104倍.
即时测评
计算:(结果用科学记数法表示)
(1)(6.5×10-9)×(5×10-4); (2)(2×10-5)÷(4×106)2.
(2)(2×10-5)÷(4×106)2
=(2×10-5)÷(16×1012)
=(2÷16)×(10-5÷1012)
=0.125×10-17
=1.25×10-18.
解:(1)(6.5×10-9)×(5×10-4)
=(6.5×5)×(10-9×10-4)
=32.5×10-13
=3.25×10-12.
当堂达标
叁
当堂达标
解:(1)0.003 009=3.009×10-3.
(2)-0.000 010 96=-1.096×10-5.
(3)0.000 329=3.29×10-4.
(4)0.000 000 004 05=4.05×10-9.
1. 用科学记数法表示下列各数.
(1)0.003 009; (2)-0.000 010 96;
(3)0.000 329; (4)0.000 000 004 05.
2.将以下用科学记数法表示的数写成小数的形式.
(1)3.02×10-5; (2)-2.14×10-7;
(3)5.7×10-6; (4)-1.07×10-8.
解:(1)3.02×10-5=3.02×0.00001=0.0000302.
(2)-2.14×10-7=-2.14×0.0000001=-0.000000214.
(3)5.7×10-6=5.7×0.000001=0.0000057.
(4)-1.07×10-8=-1.07×0.00000001=-0.0000000107.
3.计算:
(1)(-5.8×10-9)×(2×104); (2)(-4×10-2)2÷(0.5×10-3).
解:(1)(-5.8×10-9)×(2×104)
=-(5.8×2)×(10-9×104)
=-11.6×10-5
=-1.16×10-4.
(2)(-4×10-2)2÷(0.5×10-3)
=(-4)2×(10-2)2÷(0.5×10-3)
=(16×10-4)÷(0.5×10-3)
=(16÷0.5)×(10-4÷10-3)
=32×10-1=3.2.
4.为了打破国外芯片封锁,我国将加快完善集成
电路设计、制造、封测等产业链,开展EDA工具软件、半导体材料、高端芯片和专用芯片设计技术攻关,推进第三代半导体等重点项目建设.已知一块900mm2的芯片上能集成10亿个元件.
(1)每个这样的元件约占多少平方毫米
(2)每个这样的元件约占多少平方米
解:(1)10亿=10×108=1×109,
900÷(1×109)=9×10-7(mm2).
所以每个这样的元件约占9×10-7mm2.
(2)1m2=106mm2,9×10-7÷106=9×10-13(m2).
∴每个这样的元件约占9×10-13m2.
课堂小结
肆
课堂小结
用科学记数法表示绝对值小于1的正数
绝对值小于1的正数用科学记数法表示为a×10-n的形式,1≤a <10,n为原数第1个不为0的数字前面所有0的个数(包括小数点前面那个0).
课后作业
基础题:1.课后习题 第 4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
