18.5 分式方程 第2课时 分式方程的应用 课件(共26张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 18.5 分式方程 第2课时 分式方程的应用 课件(共26张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:26:04 | ||
图片预览








文档简介
(共26张PPT)
第18章 分式
18.5 分式方程
第2课时 分式方程的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
2.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题: ;
(2)工程问题: ;
路程=速度×时间
工作量=工时×工效
1.列方程解决实际问题的步骤:
;
审、设、列、解、验、答
(4)利润问题:
利润= ;
利润率= ;
总价= ;
打折后的销售价= ;
……
售价-进价
利润÷进价
售价×数量
标价×折扣
(3)数字问题: 掌握十进制数的表示法;
3.(1)一项工作甲单独做a天完成,乙单独做b天完成,甲的工作效率是 ,乙的工作效率是 ,甲、乙合作5天,一共完成工程的 .
(2)甲乙两地相距s千米,客车的速度为v千米/时,则乘坐该客车从甲地到乙地需 小时.
新知初探
贰
(1)“哪个施工队速度快”是比较两个队的 ;
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
新知初探
(4)本题中甲队和乙队的工作效率及工作时间中哪些量是已知的?哪些量是未知的?
工作效率
任务一 用分式方程解决工程问题
活动1
(2)工程问题的基本关系式是 ;
(3)在工程问题中,当总工程量没有具体数量时,看作 ;
工作量=工作时间×工作效率
单位1
注意:这里规定每个月的天数相同,半个月的天数是一个月的一半
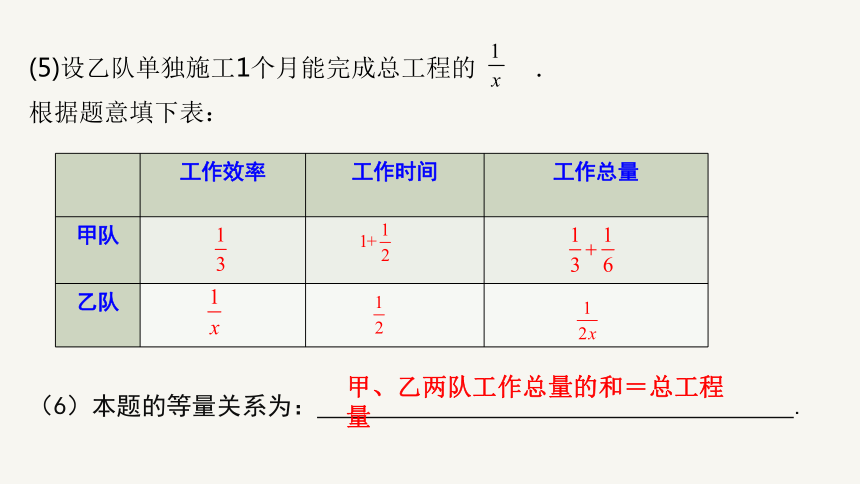
(5)设乙队单独施工1个月能完成总工程的 .
根据题意填下表:
工作效率 工作时间 工作总量
甲队
乙队
(6)本题的等量关系为: .
甲、乙两队工作总量的和=总工程量
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队单独施工速度快.
解:设乙队单独施工1个月完成总工程的 .记总工程量为1,根据工程的实际进度,列方程得
解得
方程两边同时乘以 ,得
检验:当 时,
所以,原分式方程的解为
1.审
2.设
4.解
5.验
6.答
3.列
列分式方程解应用题的一般步骤
1.审:清题意;
2.设:设出未知数;
3.列:根据相等关系出方程;
4.解:这个分式方程;
5.验:检验: (1)是否是分式方程的根;
(2)是否符合题意;
6.答:写出答案.
即时测评
甲、乙两人合做某种机械零件.已知甲每小时比乙多做6个,
甲做90个所用的时间与乙做60个所用时间相等.求甲、乙两人每小时各做零件多少个.
分析:设乙每小时做x个零件,根据题意,完成下列表格:
工作效率 工作时间 工作总量
甲
乙
90
60
等量关系为: 甲所用的时间=乙所用的时间 .
解:设乙每小时做 个零件,根据题意,得
解得
检验:当 时,
所以,原分式方程的解为
答:甲每小时做18个零件,乙每小时做12 个零件.
(2)设提速前列车的平均速度为x km/h,那么列车提速后的平均速度
为 km/h;
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度是多少
(3)用相同时间,列车提速前行驶s km,提速后比提速前多行驶50 km,那么列车提速后行驶的路程为 km;
(x+v)
任务二 用分式方程解决行程问题
活动1
(1)行程问题的基本关系式是 ;
路程=速度×时间
(s+50)
(4)“相同时间”是什么意思
(5)列车提速前所用的时间是 h,列车提速后所用的时间是 h.
注意:这里的 表示已知数据
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度是多少
设提速前列车的平均速度为 km/h,根据题意,完成下列表格:
路程 速度 时间
提速前
提速后
等量关系为: 列车提速前行驶的时间=列车提速后行驶的时间 .
解:设提速前列车的平均速度为 km/h,根据题意,得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
即时测评
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20min到达目的地.求甲乙两人的速度.
路程 速度 时间
甲
乙
6
10
分析:设甲的速度为 km/h,根据题意,完成下列表格:
等量关系为:甲所用的时间=乙所用的时间-20分钟
解:设甲的速度为 km/h ,乙的速度为 km/h,根据题意,得
解得
经检验:
所以,原分式方程的解为
答:甲的速度为 km/h ,乙的速度为6 km/h.
是原分式方程的解.
当堂达标
叁
当堂达标
1.王师傅检修一条长600米的自来水管道,计划用若干小时完成,在实际检修过程中,每小时检修管道长度是原计划的1.2倍,结果提前2小时完成任务,王师傅原计划每小时检修管道多少米?
解:设原计划每小时检修管道x米.
由题意,得 .
解得x=50.
经检验,x=50是原方程的解.且符合题意.
答:原计划每小时检修管道50米.
2.小明和小刚约定周末到某体育公园打羽毛球.他们两家到体育公园的距离分别是1200米,3000米,小刚骑自行车的速度是小明步行速度的3倍,若二人同时到达,则小明需提前4分钟出发,求小明和小刚两人的速度.
解:设小明的速度是x米/分钟,则小刚的速度是3x米/分钟,
根据题意,得 ,
解得x=50,
经检验x=50是原方程的根,故3x=150.
答:小明的速度是50米/分钟,小刚的速度是150米/分钟.
3.为了进一步丰富校园文体活动,学校准备
购进一批篮球和足球,已知每个篮球的进价比每个足
球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
解:设每个足球的进价是x元,则每个篮球的进价是(x+25)元,
依题意得 ,
解得:x=75,
经检验,x=75是原方程的解,且符合题意,
∴x+25=75+25=100.
答:每个足球的进价是75元,每个篮球的进价是100元.
课堂小结
肆
课堂小结
1、列分式方程解应用题,应该注意解题的五个 步骤。
2、列方程的关键是要在准确设元(可直接设,也可间节设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和漏写答。
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第18章 分式
18.5 分式方程
第2课时 分式方程的应用
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
2.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有4种:
(1)行程问题: ;
(2)工程问题: ;
路程=速度×时间
工作量=工时×工效
1.列方程解决实际问题的步骤:
;
审、设、列、解、验、答
(4)利润问题:
利润= ;
利润率= ;
总价= ;
打折后的销售价= ;
……
售价-进价
利润÷进价
售价×数量
标价×折扣
(3)数字问题: 掌握十进制数的表示法;
3.(1)一项工作甲单独做a天完成,乙单独做b天完成,甲的工作效率是 ,乙的工作效率是 ,甲、乙合作5天,一共完成工程的 .
(2)甲乙两地相距s千米,客车的速度为v千米/时,则乘坐该客车从甲地到乙地需 小时.
新知初探
贰
(1)“哪个施工队速度快”是比较两个队的 ;
两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,哪个队的施工速度快?
新知初探
(4)本题中甲队和乙队的工作效率及工作时间中哪些量是已知的?哪些量是未知的?
工作效率
任务一 用分式方程解决工程问题
活动1
(2)工程问题的基本关系式是 ;
(3)在工程问题中,当总工程量没有具体数量时,看作 ;
工作量=工作时间×工作效率
单位1
注意:这里规定每个月的天数相同,半个月的天数是一个月的一半
(5)设乙队单独施工1个月能完成总工程的 .
根据题意填下表:
工作效率 工作时间 工作总量
甲队
乙队
(6)本题的等量关系为: .
甲、乙两队工作总量的和=总工程量
由上可知,若乙队单独施工1个月可以完成全部任务,对比甲队1个月完成任务的 ,可知乙队单独施工速度快.
解:设乙队单独施工1个月完成总工程的 .记总工程量为1,根据工程的实际进度,列方程得
解得
方程两边同时乘以 ,得
检验:当 时,
所以,原分式方程的解为
1.审
2.设
4.解
5.验
6.答
3.列
列分式方程解应用题的一般步骤
1.审:清题意;
2.设:设出未知数;
3.列:根据相等关系出方程;
4.解:这个分式方程;
5.验:检验: (1)是否是分式方程的根;
(2)是否符合题意;
6.答:写出答案.
即时测评
甲、乙两人合做某种机械零件.已知甲每小时比乙多做6个,
甲做90个所用的时间与乙做60个所用时间相等.求甲、乙两人每小时各做零件多少个.
分析:设乙每小时做x个零件,根据题意,完成下列表格:
工作效率 工作时间 工作总量
甲
乙
90
60
等量关系为: 甲所用的时间=乙所用的时间 .
解:设乙每小时做 个零件,根据题意,得
解得
检验:当 时,
所以,原分式方程的解为
答:甲每小时做18个零件,乙每小时做12 个零件.
(2)设提速前列车的平均速度为x km/h,那么列车提速后的平均速度
为 km/h;
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度是多少
(3)用相同时间,列车提速前行驶s km,提速后比提速前多行驶50 km,那么列车提速后行驶的路程为 km;
(x+v)
任务二 用分式方程解决行程问题
活动1
(1)行程问题的基本关系式是 ;
路程=速度×时间
(s+50)
(4)“相同时间”是什么意思
(5)列车提速前所用的时间是 h,列车提速后所用的时间是 h.
注意:这里的 表示已知数据
某次列车平均提速v km/h.用相同的时间,列车提速前行驶s km,提速后比提速前多行驶50 km,提速前列车的平均速度是多少
设提速前列车的平均速度为 km/h,根据题意,完成下列表格:
路程 速度 时间
提速前
提速后
等量关系为: 列车提速前行驶的时间=列车提速后行驶的时间 .
解:设提速前列车的平均速度为 km/h,根据题意,得
方程两边乘 ,得
x(x+v)
s(x+v)=x(s+50).
解得
检验:由v,s都是正数,得
时 x(x+v)≠0.
所以,原分式方程的解为
答:提速前列车的平均速度为
km/h.
即时测评
甲、乙两人分别从距目的地6km和10km的两地同时出发,甲乙的速度比是3:4,结果甲比乙提前20min到达目的地.求甲乙两人的速度.
路程 速度 时间
甲
乙
6
10
分析:设甲的速度为 km/h,根据题意,完成下列表格:
等量关系为:甲所用的时间=乙所用的时间-20分钟
解:设甲的速度为 km/h ,乙的速度为 km/h,根据题意,得
解得
经检验:
所以,原分式方程的解为
答:甲的速度为 km/h ,乙的速度为6 km/h.
是原分式方程的解.
当堂达标
叁
当堂达标
1.王师傅检修一条长600米的自来水管道,计划用若干小时完成,在实际检修过程中,每小时检修管道长度是原计划的1.2倍,结果提前2小时完成任务,王师傅原计划每小时检修管道多少米?
解:设原计划每小时检修管道x米.
由题意,得 .
解得x=50.
经检验,x=50是原方程的解.且符合题意.
答:原计划每小时检修管道50米.
2.小明和小刚约定周末到某体育公园打羽毛球.他们两家到体育公园的距离分别是1200米,3000米,小刚骑自行车的速度是小明步行速度的3倍,若二人同时到达,则小明需提前4分钟出发,求小明和小刚两人的速度.
解:设小明的速度是x米/分钟,则小刚的速度是3x米/分钟,
根据题意,得 ,
解得x=50,
经检验x=50是原方程的根,故3x=150.
答:小明的速度是50米/分钟,小刚的速度是150米/分钟.
3.为了进一步丰富校园文体活动,学校准备
购进一批篮球和足球,已知每个篮球的进价比每个足
球的进价多25元,用2000元购进篮球的数量是用750元购进足球数量的2倍,求:每个篮球和足球的进价各多少元?
解:设每个足球的进价是x元,则每个篮球的进价是(x+25)元,
依题意得 ,
解得:x=75,
经检验,x=75是原方程的解,且符合题意,
∴x+25=75+25=100.
答:每个足球的进价是75元,每个篮球的进价是100元.
课堂小结
肆
课堂小结
1、列分式方程解应用题,应该注意解题的五个 步骤。
2、列方程的关键是要在准确设元(可直接设,也可间节设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和漏写答。
课后作业
基础题:1.课后习题 第 4,5,6题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
