第13章 三角形 本章考点复习课件(共27张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 第13章 三角形 本章考点复习课件(共27张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:27:05 | ||
图片预览





文档简介
(共27张PPT)
第13章 三角形
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在这一章,我们深入地研究了三角形的概念、相关线段与角的性质,这节课我们把这章的知识整体回顾一下.
新知初探
贰
新知初探
任务一 问题引领,回顾重点
活动1
思考后回答
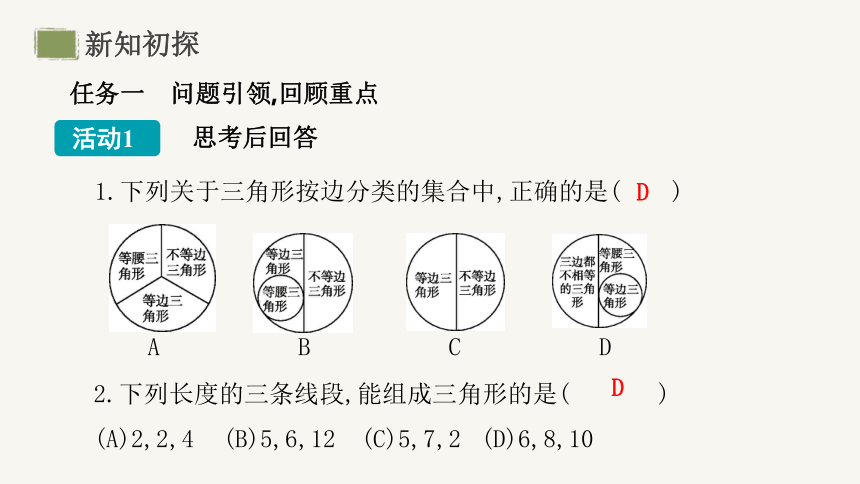
1.下列关于三角形按边分类的集合中,正确的是( )
A B C D
D
2.下列长度的三条线段,能组成三角形的是( )
(A)2,2,4 (B)5,6,12 (C)5,7,2 (D)6,8,10
D
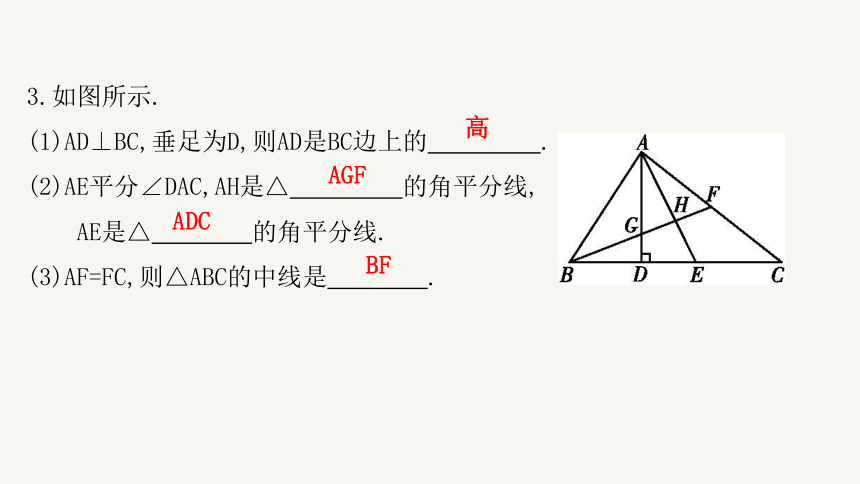
3.如图所示.
(1)AD⊥BC,垂足为D,则AD是BC边上的 .
(2)AE平分∠DAC,AH是△ 的角平分线,
AE是△ 的角平分线.
(3)AF=FC,则△ABC的中线是 .
BF
高
AGF
ADC
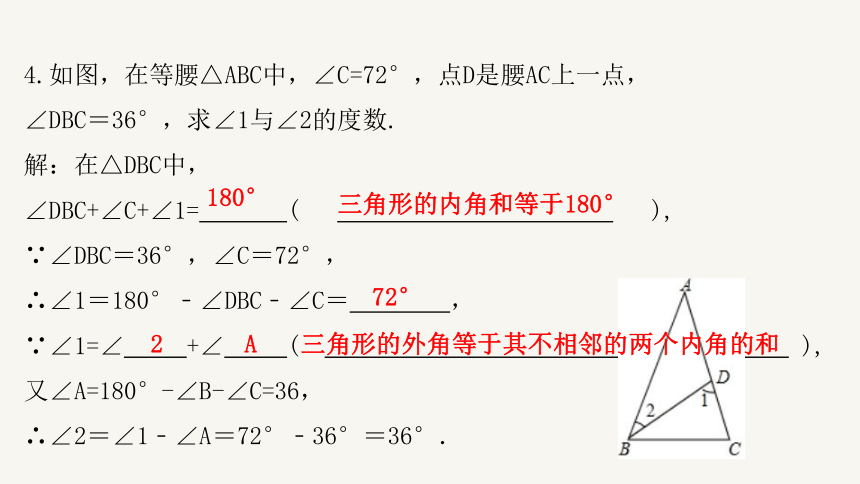
4.如图,在等腰△ABC中,∠C=72°,点D是腰AC上一点,
∠DBC=36°,求∠1与∠2的度数.
解:在△DBC中,
∠DBC+∠C+∠1= ( ),
∵∠DBC=36°,∠C=72°,
∴∠1=180°﹣∠DBC﹣∠C= ,
∵∠1=∠ +∠ ( ),
又∠A=180°-∠B-∠C=36,
∴∠2=∠1﹣∠A=72°﹣36°=36°.
180°
三角形的内角和等于180°
72°
2
A
三角形的外角等于其不相邻的两个内角的和
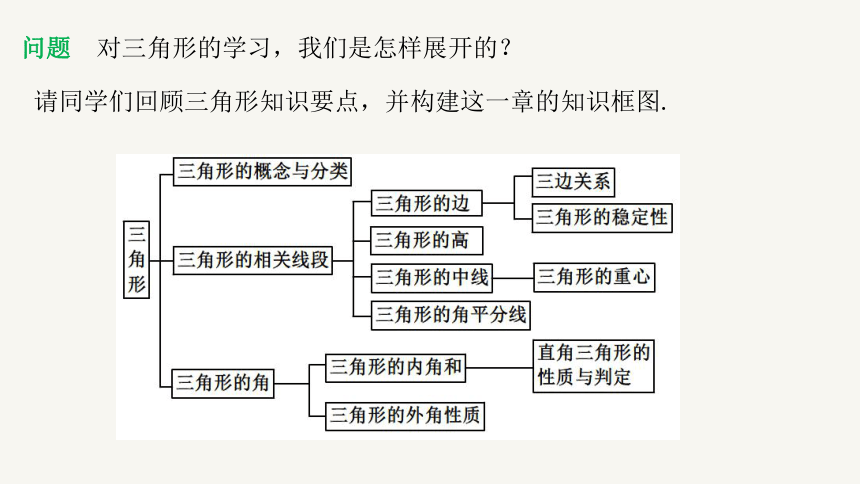
问题 对三角形的学习,我们是怎样展开的?
请同学们回顾三角形知识要点,并构建这一章的知识框图.
问题 1 若三角形的两边分别为3和5,则第三边长 m 的取值范围是__ __.
问题 2 如图,在△ABC 中,∠BAC =80°,∠ABC =60°,AE 是△ABC 的角平分线,
则∠C = °,( )
∠AEC = °.
( )
任务二 以题点知,重点突破
三角形的一个外角等于与它不相邻的两个内角的和
活动1
解决下列问题
2<m<8
40
三角形的内角和是 180°
100
范例应用
【例1】 已知等腰三角形的两边长分别为 9 和 4 ,则三角形的周长是多少?
解:如图所示.
情况一:4+4<9,不能组成三角形,此情况不成立;
情况二:9+9>4,4+9>9,所以能组成三角形,
此情况成立,9+9+4=22.
解:设较短的边长为xcm,则较长的边长为2xcm.
(1)若较短的边为腰,则x+x=2x,三角形两边之和等于第三边,不成立;
(2)若较长的边为腰,则x+2x+2x=20.
解得x=4.即2x=8.
∵4+8>8,符合三角形两边的和大于第三边.
∴能围成腰长8cm的等腰三角形.
∴这个三角形的三边分别为4cm,8cm,8cm.
变式 小明用一条长20cm的细绳围成了一个等腰三角形,
他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
【例2】如图,在△ABC中,∠ABC,∠ACB的
平分线BD,CE交于点O.
问题 若∠ABC=40°,∠ACB=60°,求∠BOC的度数.
解:∠BOC=180°-∠OBC-∠OCB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (40°+60°)
=130°.
变式一 若已知若∠A=80°,求∠BOC 的度数 .
【例2】如图,在△ABC中,∠ABC,∠ACB的
平分线BD,CE交于点O.
解:∠BOC=180°-∠OBC-∠OCB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+ ∠A
=130°.
变式二 如图,若换成两外角平分线相交于 O,则∠BOC 与∠A 又有怎样的数量关系?
解:∠BOC=180°-∠OBC-∠OCB
=180°- (∠A+∠ACB)- (∠A+∠ABC)
=180°- ∠A- ∠ACB- ∠A- ∠ABC
=180°- ∠A- (180°-∠A)
=90°- ∠A.
变式三 如图,若换成一内角与一外角平分线相交于点 O,则∠BOC 与∠A 又有怎样的数量关系?请同学们课后思考。
即时测评
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠BAC=130°,求∠E的度数;
解:(1)∵∠ACD是△ABC的外角,∠B=30°,∠BAC=130°,
∴∠ACD=∠B+∠BAC=160°,
∵CE平分∠ACD,
∴∠ECD= ∠ACD=80°,
∵∠ECD是△BCE的外角,
∴∠E+∠B=∠ECD,
∴∠E=∠ECD-∠B=50°.
(2)求证:∠BAC=∠B+2∠E.
(2)证明:∵CE平分∠ACD,
∴∠ECD=∠ECA,
∵∠ECD=∠B+∠E,∠BAC=∠ECA+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
当堂达标
叁
1. 若(a﹣3)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
2.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中错误的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线 C.∠1=∠2=∠3 D.BC是△ABE的高
当堂达标
B
C
3.适合下列条件的三角形中是直角三角形的是( )
A.∠A=∠B=∠C B.∠A:∠B:∠C=1:2:3
C.∠B=∠C=30° D.2∠A=∠B
4.组成三角形的三根棒中有两根棒长为2 cm和5 cm,则第三根棒长x的取值范围是 ,
若它的周长是奇数,则第三根棒的长为 .
B
3 cm5cm
5.如图,AD是△ABC的外角平分线,交BC的延长线于点D,若∠B=30°,∠DAE=55°,求∠ACD的度数.
解:∵∠DAE=55°,AD平分∠CAE,
∴∠CAE=110°.
∵∠CAE是△ABC的外角,∠B=30°,
∴∠ACB=110°-30°=80°.
∴∠ACD=180°-80°=100°.
6.已知:如图所示,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°,求∠C的度数.
解:∵∠BFC是△AFC的外角,△BEC是△ABE的外角,
∴∠BFC=∠A+∠C,∠BEC=∠A+∠B,
∵∠BFC比∠BEC大20°,
∴(∠A+∠C)-(∠A+∠B)=20°,即∠C-∠B=20°,
∵∠C=2∠B,
∴2∠B-∠B=20°,即∠B=20°,
∴∠C=2×20°=40°.
课堂小结
肆
课堂小结
1.本节课你最大的收获是什么?
2.还有哪些疑惑?
课后作业
基础题:1.课后复习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后复习题第4题
谢
谢
第13章 三角形
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在这一章,我们深入地研究了三角形的概念、相关线段与角的性质,这节课我们把这章的知识整体回顾一下.
新知初探
贰
新知初探
任务一 问题引领,回顾重点
活动1
思考后回答
1.下列关于三角形按边分类的集合中,正确的是( )
A B C D
D
2.下列长度的三条线段,能组成三角形的是( )
(A)2,2,4 (B)5,6,12 (C)5,7,2 (D)6,8,10
D
3.如图所示.
(1)AD⊥BC,垂足为D,则AD是BC边上的 .
(2)AE平分∠DAC,AH是△ 的角平分线,
AE是△ 的角平分线.
(3)AF=FC,则△ABC的中线是 .
BF
高
AGF
ADC
4.如图,在等腰△ABC中,∠C=72°,点D是腰AC上一点,
∠DBC=36°,求∠1与∠2的度数.
解:在△DBC中,
∠DBC+∠C+∠1= ( ),
∵∠DBC=36°,∠C=72°,
∴∠1=180°﹣∠DBC﹣∠C= ,
∵∠1=∠ +∠ ( ),
又∠A=180°-∠B-∠C=36,
∴∠2=∠1﹣∠A=72°﹣36°=36°.
180°
三角形的内角和等于180°
72°
2
A
三角形的外角等于其不相邻的两个内角的和
问题 对三角形的学习,我们是怎样展开的?
请同学们回顾三角形知识要点,并构建这一章的知识框图.
问题 1 若三角形的两边分别为3和5,则第三边长 m 的取值范围是__ __.
问题 2 如图,在△ABC 中,∠BAC =80°,∠ABC =60°,AE 是△ABC 的角平分线,
则∠C = °,( )
∠AEC = °.
( )
任务二 以题点知,重点突破
三角形的一个外角等于与它不相邻的两个内角的和
活动1
解决下列问题
2<m<8
40
三角形的内角和是 180°
100
范例应用
【例1】 已知等腰三角形的两边长分别为 9 和 4 ,则三角形的周长是多少?
解:如图所示.
情况一:4+4<9,不能组成三角形,此情况不成立;
情况二:9+9>4,4+9>9,所以能组成三角形,
此情况成立,9+9+4=22.
解:设较短的边长为xcm,则较长的边长为2xcm.
(1)若较短的边为腰,则x+x=2x,三角形两边之和等于第三边,不成立;
(2)若较长的边为腰,则x+2x+2x=20.
解得x=4.即2x=8.
∵4+8>8,符合三角形两边的和大于第三边.
∴能围成腰长8cm的等腰三角形.
∴这个三角形的三边分别为4cm,8cm,8cm.
变式 小明用一条长20cm的细绳围成了一个等腰三角形,
他想使这个三角形的一边长是另一边长的2倍,那么这个三角形的各边的长分别是多少?
【例2】如图,在△ABC中,∠ABC,∠ACB的
平分线BD,CE交于点O.
问题 若∠ABC=40°,∠ACB=60°,求∠BOC的度数.
解:∠BOC=180°-∠OBC-∠OCB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (40°+60°)
=130°.
变式一 若已知若∠A=80°,求∠BOC 的度数 .
【例2】如图,在△ABC中,∠ABC,∠ACB的
平分线BD,CE交于点O.
解:∠BOC=180°-∠OBC-∠OCB
=180°- ∠ABC- ∠ACB
=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)
=90°+ ∠A
=130°.
变式二 如图,若换成两外角平分线相交于 O,则∠BOC 与∠A 又有怎样的数量关系?
解:∠BOC=180°-∠OBC-∠OCB
=180°- (∠A+∠ACB)- (∠A+∠ABC)
=180°- ∠A- ∠ACB- ∠A- ∠ABC
=180°- ∠A- (180°-∠A)
=90°- ∠A.
变式三 如图,若换成一内角与一外角平分线相交于点 O,则∠BOC 与∠A 又有怎样的数量关系?请同学们课后思考。
即时测评
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠BAC=130°,求∠E的度数;
解:(1)∵∠ACD是△ABC的外角,∠B=30°,∠BAC=130°,
∴∠ACD=∠B+∠BAC=160°,
∵CE平分∠ACD,
∴∠ECD= ∠ACD=80°,
∵∠ECD是△BCE的外角,
∴∠E+∠B=∠ECD,
∴∠E=∠ECD-∠B=50°.
(2)求证:∠BAC=∠B+2∠E.
(2)证明:∵CE平分∠ACD,
∴∠ECD=∠ECA,
∵∠ECD=∠B+∠E,∠BAC=∠ECA+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
当堂达标
叁
1. 若(a﹣3)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A.12 B.15 C.12或15 D.18
2.如图,在△ABC中,∠C=90°,D,E是AC上两点,且AE=DE,BD平分∠EBC,那么下列说法中错误的是( )
A.BE是△ABD的中线 B.BD是△BCE的角平分线 C.∠1=∠2=∠3 D.BC是△ABE的高
当堂达标
B
C
3.适合下列条件的三角形中是直角三角形的是( )
A.∠A=∠B=∠C B.∠A:∠B:∠C=1:2:3
C.∠B=∠C=30° D.2∠A=∠B
4.组成三角形的三根棒中有两根棒长为2 cm和5 cm,则第三根棒长x的取值范围是 ,
若它的周长是奇数,则第三根棒的长为 .
B
3 cm
5.如图,AD是△ABC的外角平分线,交BC的延长线于点D,若∠B=30°,∠DAE=55°,求∠ACD的度数.
解:∵∠DAE=55°,AD平分∠CAE,
∴∠CAE=110°.
∵∠CAE是△ABC的外角,∠B=30°,
∴∠ACB=110°-30°=80°.
∴∠ACD=180°-80°=100°.
6.已知:如图所示,点E在AC上,点F在AB上,BE,CF交于点O,且∠C=2∠B,∠BFC比∠BEC大20°,求∠C的度数.
解:∵∠BFC是△AFC的外角,△BEC是△ABE的外角,
∴∠BFC=∠A+∠C,∠BEC=∠A+∠B,
∵∠BFC比∠BEC大20°,
∴(∠A+∠C)-(∠A+∠B)=20°,即∠C-∠B=20°,
∵∠C=2∠B,
∴2∠B-∠B=20°,即∠B=20°,
∴∠C=2×20°=40°.
课堂小结
肆
课堂小结
1.本节课你最大的收获是什么?
2.还有哪些疑惑?
课后作业
基础题:1.课后复习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后复习题第4题
谢
谢
同课章节目录
