第16章 整式的乘法 本章考点复习课件(共26张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 第16章 整式的乘法 本章考点复习课件(共26张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:29:18 | ||
图片预览







文档简介
(共26张PPT)
第16章 整式的乘法
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
这段时间,我们学习了整式的乘法,大家对本章内容掌握得怎样?还有哪些疑惑的地方?通过这一节课的复习,希望大家有进一步的认识与收获.
新知初探
贰
计算:
(1)2xy2 (-3x2y3)2
(2)(-2t) (3t+t2-1)
(3)(2a+b)(a-2b)
(4)(2x+y-1)(2x+y+1)
(5)(36x4y3-24x3y2+6x2y2)÷(-6x2y)
新知初探
=2a2-4ab+ab-2b2=2a2-3ab-2b2
活动1
复习回顾
=2xy2 9x4y6=18x5y8
=(-2t) 3t+(-2t) t2-(-2t)=-6t2-2t3+2t
=[(2x+y)-1][(2x+y)+1]=(2x+y)2-1=4x2+4xy+y2-1.
=-6x2y2+4xy-y
思考各题中都运用到我们学过的哪些运算法则?
它们之间有怎样的关系?
要点1 幂的运算性质
字母表达式
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
am·an=am+n
(am)n=amn
(ab)n=anbn
am ÷ an=am-n
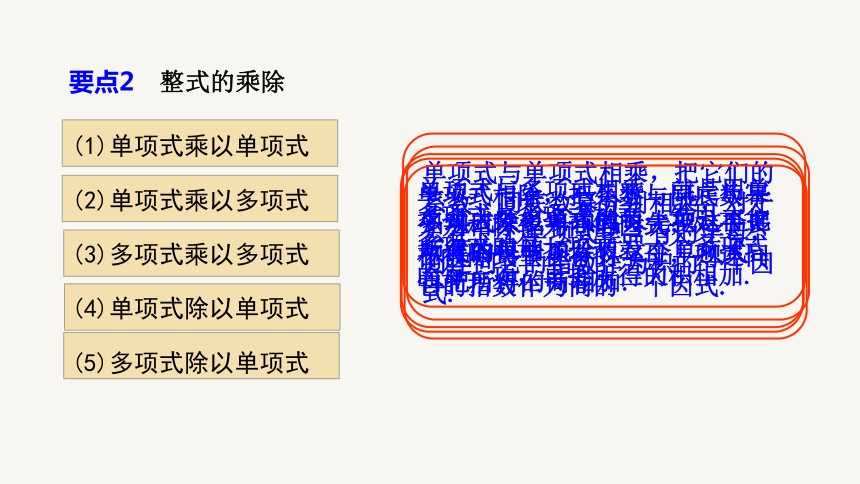
要点2 整式的乘除
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
(4)单项式除以单项式
(5)多项式除以单项式
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
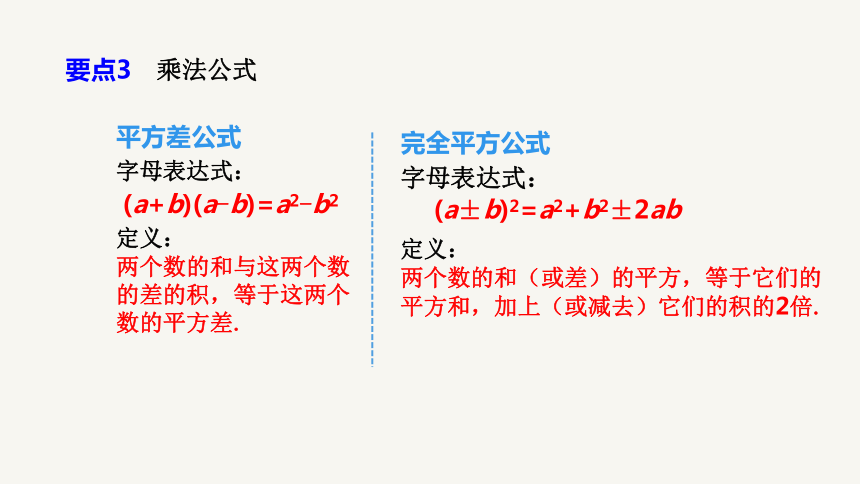
平方差公式
字母表达式:
定义:
两个数的和与这两个数的差的积,等于这两个数的平方差.
完全平方公式
字母表达式:
定义:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)(a-b)=a2-b2
(a±b)2=a2+b2±2ab
要点3 乘法公式
活动2
知识建构
根据以上问题的解决梳理一下本单元知识点,然后与同伴交流.
=4(x2+1)-4x2-25
=4x2+4-4x2-25
=-21.
=6a3 b6÷12a3b2
= ab3.
=4(x2+2x+1)-(4x2-25)
=4x2+8x+4-4x2+25
=8x+29.
活动3
典型例题
例1 下列计算是否正确?如果有错,请指出错误的地方,并把正确的计算过程写下来:
(1)(2a)3 b6÷12a3b2; (2)4(x+1)2-(2x+5)(2x-5).
订正:
原式=8a3 b6÷12a3b2
= 2/3 b4.
【例2】如图1,在边长为a的正方形中剪去一个
边长为b的小正方形(a>b),把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图2),利用这两幅图形面积,可以验证的乘法公式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a+b)2=a2+2ab+b2
C.a(a+b)=a2+ab
D.(a+b)(a﹣b)=a2﹣b2
D
a2﹣b2
a-b
(2a+2b)(a-b)
= ×2(a+b)(a-b)
= (a+b)(a-b)
a-b
【例3】先化简,再求值.
(x﹣y)2+(3x﹣y)(x+y)﹣(x﹣2y)(x+2y),
其中x,y满足(x+3)2+|y﹣2|=0.
解:(x﹣y)2+(3x﹣y)(x+y)﹣(x﹣2y)(x+2y)
=x2﹣2xy+y2+3x2+2xy﹣y2﹣x2+4y2
=3x2+4y2,
∵(x+3)2+|y﹣2|=0,
∴x+3=0,y﹣2=0,解得x=﹣3,y=2,
当x=﹣3,y=2时,
原式=3×(﹣3)2+4×22=3×9+4×4=27+16=43.
【例4】阅读:已知a+b=-4,ab=3,求a2+b2的值.
解:∵a+b=-4,ab=3,
∴a2+b2=(a+b)2-2ab=(-4)2-2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a-b=-3,ab=-2,求a2+b2的值.
解:(1)∵a-b=-3,ab=-2,
∴a2+b2=(a-b)2+2ab=(-3)2+2×(-2)=5;
(2)已知(2025-a)(2026-a)=2047,求(2025-a)2+(2026-a)2的值.
解:(2)(2025-a)2+(2026-a)2
=[(2025-a)-(2026-a)]2+2(2025-a)(2026-a)
=(-1)2+2(2025-a)(2026-a),
∵(2025-a)(2026-a)=2047,
∴原式=1+2×2047=4095.
常见的完全平方公式的变形
完全平方公式 变形
(a+b)2=a2+ 2ab+b2 ①a2+b2=(a+b)2-2ab
②2ab=(a+b)2-(a2+b2)
(a-b)2=a2- 2ab+b2 ①a2+b2=(a-b)2+2ab
②2ab=(a2+b2)-(a-b)2
③(a-b)2=(a+b)2-4ab
④(a+b)2=(a-b)2+4ab
即时测评
1.已知x+y=10,xy=24,则x2+y2=_____
52
变式:已知 则 _____
98
18或-18
变式:如果x2+6x+m2是完全平方式,则m的值是_____
3.已知ab=2,(a+b)2=9,则(a-b)2的值为______
变式:若题目条件不变,则a-b的值为_____
±1
1
2.如果x2+kx+81是运用完全平方式得到的结果, 则k=______
3或-3
当堂达标
叁
当堂达标
1. 下列计算正确的是( )
A.a2 a3=a6 B.(-2ab)2=4a2b2
C.(a2)3=a5 D.3a3b2÷a2b2=3ab
2.下列运算正确的是( )
A.-a(a-b)=-a2-ab B.(2ab)2÷a2b=4ab
C.2ab 3a=6a2b D.(a-1)(1-a)=a2-1
B
C
4.(1)若2m=a,32n=b,m,n为正整数,则23m+10n= .
(2)若a+3b-2=0,则3a 27b= .
9
3.直接依据图中图形面积之间的关系,
通过计算可以表示的等式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab
D.(a+b)(a﹣b)=a2﹣b2
B
a3b2
5.计算:
(1)3a2(a3b2-2a)-4a(-a2b)2;
(2)(2x-5)(2x+5)-(2x+1)(2x-3).
解:(1)原式=3a5b2-6a3-4a a4b2
=3a5b2-6a3-4a5b2
=-6a3-a5b2.
(2)原式=4x2-25-(4x2-6x+2x-3)
=4x2-25-4x2+6x-2x+3
=4x-22.
6.已知多项式(x2+mx+n)(x2-3x+2)展开后,
不含x3项和x项,试将代数式[(m-3n)(m+3n)-(m-n)2+2n(m-n)]÷4n化简求值。
解:(x2+mx+n)(x2-3x+2)
=x4-3x3+2x2+mx3-3mx2+2mx+nx2-3nx+2n
=x4-(3-m)x3+(2-3m+n)x2+(2m-3n)x+2n.
由题意得,3-m=0,2m-3n=0,
解得m=3,n=2.
[(m-3n)(m+3n)-(m-n)2+2n(m-n)]÷4n
=[m2-9n2-m2+2mn-n2+2mn-2n2]÷4n
=(4mn-12n2)÷4n
=m-3n=3-6=-3
课堂小结
肆
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
课后作业
基础题:1.课后复习题 第3,4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
第16章 整式的乘法
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
这段时间,我们学习了整式的乘法,大家对本章内容掌握得怎样?还有哪些疑惑的地方?通过这一节课的复习,希望大家有进一步的认识与收获.
新知初探
贰
计算:
(1)2xy2 (-3x2y3)2
(2)(-2t) (3t+t2-1)
(3)(2a+b)(a-2b)
(4)(2x+y-1)(2x+y+1)
(5)(36x4y3-24x3y2+6x2y2)÷(-6x2y)
新知初探
=2a2-4ab+ab-2b2=2a2-3ab-2b2
活动1
复习回顾
=2xy2 9x4y6=18x5y8
=(-2t) 3t+(-2t) t2-(-2t)=-6t2-2t3+2t
=[(2x+y)-1][(2x+y)+1]=(2x+y)2-1=4x2+4xy+y2-1.
=-6x2y2+4xy-y
思考各题中都运用到我们学过的哪些运算法则?
它们之间有怎样的关系?
要点1 幂的运算性质
字母表达式
同底数幂的乘法
幂的乘方
积的乘方
同底数幂的除法
am·an=am+n
(am)n=amn
(ab)n=anbn
am ÷ an=am-n
要点2 整式的乘除
(1)单项式乘以单项式
(2)单项式乘以多项式
(3)多项式乘以多项式
(4)单项式除以单项式
(5)多项式除以单项式
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
单项式相除,把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
平方差公式
字母表达式:
定义:
两个数的和与这两个数的差的积,等于这两个数的平方差.
完全平方公式
字母表达式:
定义:
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(a+b)(a-b)=a2-b2
(a±b)2=a2+b2±2ab
要点3 乘法公式
活动2
知识建构
根据以上问题的解决梳理一下本单元知识点,然后与同伴交流.
=4(x2+1)-4x2-25
=4x2+4-4x2-25
=-21.
=6a3 b6÷12a3b2
= ab3.
=4(x2+2x+1)-(4x2-25)
=4x2+8x+4-4x2+25
=8x+29.
活动3
典型例题
例1 下列计算是否正确?如果有错,请指出错误的地方,并把正确的计算过程写下来:
(1)(2a)3 b6÷12a3b2; (2)4(x+1)2-(2x+5)(2x-5).
订正:
原式=8a3 b6÷12a3b2
= 2/3 b4.
【例2】如图1,在边长为a的正方形中剪去一个
边长为b的小正方形(a>b),把剩下部分沿图1中的虚线剪开后重新拼成一个梯形(如图2),利用这两幅图形面积,可以验证的乘法公式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a+b)2=a2+2ab+b2
C.a(a+b)=a2+ab
D.(a+b)(a﹣b)=a2﹣b2
D
a2﹣b2
a-b
(2a+2b)(a-b)
= ×2(a+b)(a-b)
= (a+b)(a-b)
a-b
【例3】先化简,再求值.
(x﹣y)2+(3x﹣y)(x+y)﹣(x﹣2y)(x+2y),
其中x,y满足(x+3)2+|y﹣2|=0.
解:(x﹣y)2+(3x﹣y)(x+y)﹣(x﹣2y)(x+2y)
=x2﹣2xy+y2+3x2+2xy﹣y2﹣x2+4y2
=3x2+4y2,
∵(x+3)2+|y﹣2|=0,
∴x+3=0,y﹣2=0,解得x=﹣3,y=2,
当x=﹣3,y=2时,
原式=3×(﹣3)2+4×22=3×9+4×4=27+16=43.
【例4】阅读:已知a+b=-4,ab=3,求a2+b2的值.
解:∵a+b=-4,ab=3,
∴a2+b2=(a+b)2-2ab=(-4)2-2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a-b=-3,ab=-2,求a2+b2的值.
解:(1)∵a-b=-3,ab=-2,
∴a2+b2=(a-b)2+2ab=(-3)2+2×(-2)=5;
(2)已知(2025-a)(2026-a)=2047,求(2025-a)2+(2026-a)2的值.
解:(2)(2025-a)2+(2026-a)2
=[(2025-a)-(2026-a)]2+2(2025-a)(2026-a)
=(-1)2+2(2025-a)(2026-a),
∵(2025-a)(2026-a)=2047,
∴原式=1+2×2047=4095.
常见的完全平方公式的变形
完全平方公式 变形
(a+b)2=a2+ 2ab+b2 ①a2+b2=(a+b)2-2ab
②2ab=(a+b)2-(a2+b2)
(a-b)2=a2- 2ab+b2 ①a2+b2=(a-b)2+2ab
②2ab=(a2+b2)-(a-b)2
③(a-b)2=(a+b)2-4ab
④(a+b)2=(a-b)2+4ab
即时测评
1.已知x+y=10,xy=24,则x2+y2=_____
52
变式:已知 则 _____
98
18或-18
变式:如果x2+6x+m2是完全平方式,则m的值是_____
3.已知ab=2,(a+b)2=9,则(a-b)2的值为______
变式:若题目条件不变,则a-b的值为_____
±1
1
2.如果x2+kx+81是运用完全平方式得到的结果, 则k=______
3或-3
当堂达标
叁
当堂达标
1. 下列计算正确的是( )
A.a2 a3=a6 B.(-2ab)2=4a2b2
C.(a2)3=a5 D.3a3b2÷a2b2=3ab
2.下列运算正确的是( )
A.-a(a-b)=-a2-ab B.(2ab)2÷a2b=4ab
C.2ab 3a=6a2b D.(a-1)(1-a)=a2-1
B
C
4.(1)若2m=a,32n=b,m,n为正整数,则23m+10n= .
(2)若a+3b-2=0,则3a 27b= .
9
3.直接依据图中图形面积之间的关系,
通过计算可以表示的等式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.(a+b)2=a2+2ab+b2
C.2a(a+b)=2a2+2ab
D.(a+b)(a﹣b)=a2﹣b2
B
a3b2
5.计算:
(1)3a2(a3b2-2a)-4a(-a2b)2;
(2)(2x-5)(2x+5)-(2x+1)(2x-3).
解:(1)原式=3a5b2-6a3-4a a4b2
=3a5b2-6a3-4a5b2
=-6a3-a5b2.
(2)原式=4x2-25-(4x2-6x+2x-3)
=4x2-25-4x2+6x-2x+3
=4x-22.
6.已知多项式(x2+mx+n)(x2-3x+2)展开后,
不含x3项和x项,试将代数式[(m-3n)(m+3n)-(m-n)2+2n(m-n)]÷4n化简求值。
解:(x2+mx+n)(x2-3x+2)
=x4-3x3+2x2+mx3-3mx2+2mx+nx2-3nx+2n
=x4-(3-m)x3+(2-3m+n)x2+(2m-3n)x+2n.
由题意得,3-m=0,2m-3n=0,
解得m=3,n=2.
[(m-3n)(m+3n)-(m-n)2+2n(m-n)]÷4n
=[m2-9n2-m2+2mn-n2+2mn-2n2]÷4n
=(4mn-12n2)÷4n
=m-3n=3-6=-3
课堂小结
肆
课堂小结
(1)本节课主要学习了哪些知识 学习了哪些数学思想和方法
(2)本节课还有哪些疑惑 请同学们说一说.
课后作业
基础题:1.课后复习题 第3,4,5题。
提高题:2.请学有余力的同学完成课后习题第8题
谢
谢
同课章节目录
