第17章 因式分解 本章考点复习课件(共25张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 第17章 因式分解 本章考点复习课件(共25张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:29:41 | ||
图片预览








文档简介
(共25张PPT)
第17章 因式分解
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
1.把下列各式分解因式:
(1)m2+m= ;
(2)2a(b+c)-3(b+c)= ;
(3)x2﹣9= ;
(4)a2+2a+1= ;
(5)x3y﹣6x2y+9xy=
情境导入
m(m+1)
(b+c)(2a-3)
(x+3)(x﹣3)
(a+1)2
xy(x﹣3)2
完全平方公式:
2.回答下列问题
(1)什么是因式分解?因式分解与整式的乘法有什么关系?
把一个多项式化成几个整式的积的形式.
因式分解
整式乘法
和
积
(2)因式分解有哪些方法?
提公因式法:pa+pb+pc=p(a+b+c)
平方差公式:a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
新知初探
贰
新知初探
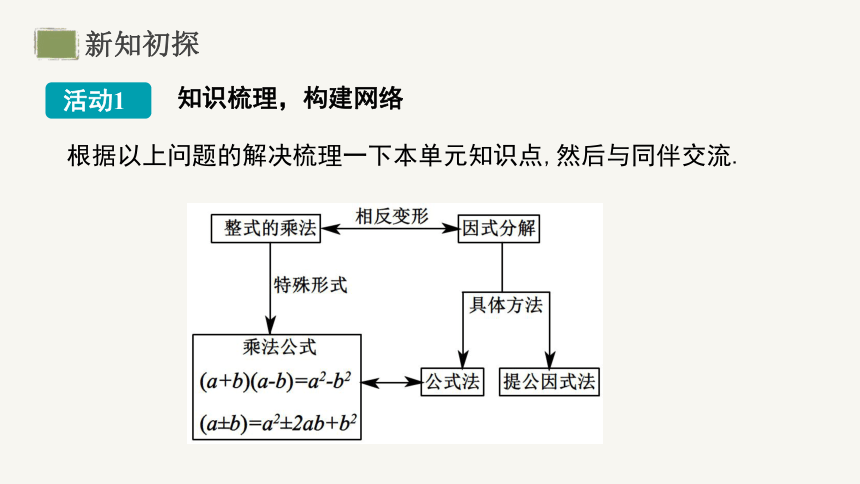
活动1
知识梳理,构建网络
根据以上问题的解决梳理一下本单元知识点,然后与同伴交流.
【例1】判断下列各式哪些是整式乘法,哪些是因式分解,哪些两者都不是
(1)ax+bx+cx+m=(a+b+c)x+m.
(2)mx2-2mx+m=m(x-1)2.
(3)x(2x-y)=2x2-xy.
(4)x2-4xy+4y2=(x-2y)2.
(5)x2-y2-1=(x+y)(x-y)-1.
(6)(x-2)(x+2)=x2-4.
(7)m2+1=m(m+ ).
(8)a2-4b2=(a-2b)(a+2b).
两者都不是
活动2
典例剖析,巩固提升
因式分解
整式乘法
因式分解
两者都不是
整式乘法
两者都不是
因式分解
(3)3ax2-6axy+3ay2
=3a(x2-2xy+y2)
=3a(x-y)2.
解:(1)5x2y-25x2y2+40x3y=5x2y(1-5y+8x).
【例2】把下列各式因式分解:
(1)5x2y-25x2y2+40x3y; (2)-2x4+32x2;
(3)3ax2-6axy+3ay2.
(2)-2x4+32x2
=-2x2(x2-16)
=-2x2(x+4)(x-4).
因式分解的三个步骤
(1)先看各项有无公因式,有公因式的先提取公因式.
(2)提公因式后看多项式的项数.
①若多项式为两项,则考虑用平方差公式因式分解.
②若多项式为三项,则考虑用完全平方公式因式分解.
归纳总结
【例3】因式分解:
(1)x4-16 ; (2)9(3m+2n)2-4(m-2n)2;
解:(1)x4-16
=(x2+4)(x2-4)
=(x2+4)(x+2)(x-2).
(2)9(3m+2n)2-4(m-2n)2
=[3(3m+2n)]2-[2(m-2n)]2
=[3(3m+2n)-2(m-2n)][3(3m+2n)+2(m-2n)]
=(7m+10n)(11m+2n).
解:(3)4a2b(a-b)+4ab(b-a)+b(a-b)
=b(a-b)(4a2-4a+1)
=b(a-b)(2a-1)2.
【例3】因式分解:
(3)4a2b(a-b)+4ab(b-a)+b(a-b) ;
应用整体的数学思想
解:(a2+b2)2-4a2b2=0,
(a2+b2+2ab)(a2+b2-2ab)=0,
(a+b)2(a-b)2=0,
因为a,b是△ABC的边,所以a+b>0,
所以(a-b)2=0,所以a=b,
所以△ABC是等腰三角形.
活动3
拓展应用,训练思维
【例4】若a,b,c为△ABC的三边,且(a2+b2)2-4a2b2=0,判断△ABC的形状,并说明理由.
【例5】已知:a2+b2-2a+4b+5=0,求a与b的值.
解:a2+b2-2a+4b+5
= a2-2a+1+ b2+4b+4
=(a-1)2+(b+2)2 =0,
因为(a-1)2≥0,(b+2)2≥0,
所以a-1=0,b+2=0,
所以a=1,b=-2.
根据以上解题方法,解答以下问题:
(1)若a2+2a+b2﹣6b+10=0,求a+b的值.
解:(1)∵a2+2a+b2﹣6b+10=0,
∴a2+2a+1+b2-6b+9=0,
∴(a+1)2+(b﹣3)2=0,
∴a=﹣1,b=3,
∴a+b=2.
根据以上解题方法,解答以下问题:
(1)若a2+2a+b2﹣6b+10=0,求a+b的值.
解:(2)x2+y2﹣2x﹣4y+16
=(x2﹣2x+1)+(y2﹣4y+4)+11
=(x﹣1)2+(y﹣2)2+11.
∵(x﹣1)2≥0,(y﹣2)2≥0,
∴(x﹣1)2+(y﹣2)2+11≥11,
所以多项式x2+y2﹣2x﹣4y+16的值总为正数.
【例5】(2)试说明不论x,y取任何实数,
多项式x2+y2﹣2x﹣4y+16的值总为正数.
当堂达标
叁
当堂达标
1. 下列各式从左到右的变形中,是因式分解的为( )
A.x(a﹣b)=ax﹣bx
B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.x2﹣1=(x+1)(x﹣1)
D.ax+bx+c=x(a+b)+c
2.下列各因式分解正确的是( )
(A)-x2+(-2)2=(x-2)(x+2) (B)x2+2x-1=(x-1)2
(C)4x2-4x+1=(2x-1)2 (D)x2-4x=2(x+2)(x-2)
3.已知xy=3,x-y=-2,则代数式x2y-xy2的值是 .
C
C
-6
4.分解因式:
(1)-2a2+8ab-8b2; (2)a2(x-1)+b2(1-x); (3)(m2+n2)2-4m2n2.
解:(1)-2a2+8ab-8b2
=-2(a2-4ab+4b2)
=-2(a-2b)2.
(2)a2(x-1)+b2(1-x)
=(x-1)(a2-b2)
=(x-1)(a-b)(a+b).
(3)(m2+n2)2-4m2n2
=(m2+n2+2mn)(m2+n2-2mn)
=(m+n)2(m-n)2.
5.已知:x+y=5,(x-2)(y-2)=-3.
求下列代数式的的值.
(1)xy;
(2)x2+xy+5y;
(3)3x3y+6x2y2+3xy3.
解:(1)∵(x-2)(y-2)=-3,
∴xy-2(x+y)+4=-3,
∵x+y=5,∴xy=3.
(2)x2+xy+5y=x(x+y)+5y,
∵x+y=5,
∴原式=5x+5y=5(x+y)=5×5=25.
(3)3x3y+6x2y2+3xy3=3xy(x2+2xy+y2)=3xy(x+y)2,
当x+y=5,xy=3时,原式=3×3×52=225.
课堂小结
肆
课堂小结
1.本节课你学到了哪些知识?
2.你还有哪些疑问?
3.你在因式分解方面有哪些收获和体会?
课后作业
基础题:1.课后复习题 第 3,4,5题。
提高题:2.请学有余力的同学完成课后复习题第7题
谢
谢
第17章 因式分解
本章考点复习
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
1.把下列各式分解因式:
(1)m2+m= ;
(2)2a(b+c)-3(b+c)= ;
(3)x2﹣9= ;
(4)a2+2a+1= ;
(5)x3y﹣6x2y+9xy=
情境导入
m(m+1)
(b+c)(2a-3)
(x+3)(x﹣3)
(a+1)2
xy(x﹣3)2
完全平方公式:
2.回答下列问题
(1)什么是因式分解?因式分解与整式的乘法有什么关系?
把一个多项式化成几个整式的积的形式.
因式分解
整式乘法
和
积
(2)因式分解有哪些方法?
提公因式法:pa+pb+pc=p(a+b+c)
平方差公式:a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
新知初探
贰
新知初探
活动1
知识梳理,构建网络
根据以上问题的解决梳理一下本单元知识点,然后与同伴交流.
【例1】判断下列各式哪些是整式乘法,哪些是因式分解,哪些两者都不是
(1)ax+bx+cx+m=(a+b+c)x+m.
(2)mx2-2mx+m=m(x-1)2.
(3)x(2x-y)=2x2-xy.
(4)x2-4xy+4y2=(x-2y)2.
(5)x2-y2-1=(x+y)(x-y)-1.
(6)(x-2)(x+2)=x2-4.
(7)m2+1=m(m+ ).
(8)a2-4b2=(a-2b)(a+2b).
两者都不是
活动2
典例剖析,巩固提升
因式分解
整式乘法
因式分解
两者都不是
整式乘法
两者都不是
因式分解
(3)3ax2-6axy+3ay2
=3a(x2-2xy+y2)
=3a(x-y)2.
解:(1)5x2y-25x2y2+40x3y=5x2y(1-5y+8x).
【例2】把下列各式因式分解:
(1)5x2y-25x2y2+40x3y; (2)-2x4+32x2;
(3)3ax2-6axy+3ay2.
(2)-2x4+32x2
=-2x2(x2-16)
=-2x2(x+4)(x-4).
因式分解的三个步骤
(1)先看各项有无公因式,有公因式的先提取公因式.
(2)提公因式后看多项式的项数.
①若多项式为两项,则考虑用平方差公式因式分解.
②若多项式为三项,则考虑用完全平方公式因式分解.
归纳总结
【例3】因式分解:
(1)x4-16 ; (2)9(3m+2n)2-4(m-2n)2;
解:(1)x4-16
=(x2+4)(x2-4)
=(x2+4)(x+2)(x-2).
(2)9(3m+2n)2-4(m-2n)2
=[3(3m+2n)]2-[2(m-2n)]2
=[3(3m+2n)-2(m-2n)][3(3m+2n)+2(m-2n)]
=(7m+10n)(11m+2n).
解:(3)4a2b(a-b)+4ab(b-a)+b(a-b)
=b(a-b)(4a2-4a+1)
=b(a-b)(2a-1)2.
【例3】因式分解:
(3)4a2b(a-b)+4ab(b-a)+b(a-b) ;
应用整体的数学思想
解:(a2+b2)2-4a2b2=0,
(a2+b2+2ab)(a2+b2-2ab)=0,
(a+b)2(a-b)2=0,
因为a,b是△ABC的边,所以a+b>0,
所以(a-b)2=0,所以a=b,
所以△ABC是等腰三角形.
活动3
拓展应用,训练思维
【例4】若a,b,c为△ABC的三边,且(a2+b2)2-4a2b2=0,判断△ABC的形状,并说明理由.
【例5】已知:a2+b2-2a+4b+5=0,求a与b的值.
解:a2+b2-2a+4b+5
= a2-2a+1+ b2+4b+4
=(a-1)2+(b+2)2 =0,
因为(a-1)2≥0,(b+2)2≥0,
所以a-1=0,b+2=0,
所以a=1,b=-2.
根据以上解题方法,解答以下问题:
(1)若a2+2a+b2﹣6b+10=0,求a+b的值.
解:(1)∵a2+2a+b2﹣6b+10=0,
∴a2+2a+1+b2-6b+9=0,
∴(a+1)2+(b﹣3)2=0,
∴a=﹣1,b=3,
∴a+b=2.
根据以上解题方法,解答以下问题:
(1)若a2+2a+b2﹣6b+10=0,求a+b的值.
解:(2)x2+y2﹣2x﹣4y+16
=(x2﹣2x+1)+(y2﹣4y+4)+11
=(x﹣1)2+(y﹣2)2+11.
∵(x﹣1)2≥0,(y﹣2)2≥0,
∴(x﹣1)2+(y﹣2)2+11≥11,
所以多项式x2+y2﹣2x﹣4y+16的值总为正数.
【例5】(2)试说明不论x,y取任何实数,
多项式x2+y2﹣2x﹣4y+16的值总为正数.
当堂达标
叁
当堂达标
1. 下列各式从左到右的变形中,是因式分解的为( )
A.x(a﹣b)=ax﹣bx
B.x2﹣1+y2=(x﹣1)(x+1)+y2
C.x2﹣1=(x+1)(x﹣1)
D.ax+bx+c=x(a+b)+c
2.下列各因式分解正确的是( )
(A)-x2+(-2)2=(x-2)(x+2) (B)x2+2x-1=(x-1)2
(C)4x2-4x+1=(2x-1)2 (D)x2-4x=2(x+2)(x-2)
3.已知xy=3,x-y=-2,则代数式x2y-xy2的值是 .
C
C
-6
4.分解因式:
(1)-2a2+8ab-8b2; (2)a2(x-1)+b2(1-x); (3)(m2+n2)2-4m2n2.
解:(1)-2a2+8ab-8b2
=-2(a2-4ab+4b2)
=-2(a-2b)2.
(2)a2(x-1)+b2(1-x)
=(x-1)(a2-b2)
=(x-1)(a-b)(a+b).
(3)(m2+n2)2-4m2n2
=(m2+n2+2mn)(m2+n2-2mn)
=(m+n)2(m-n)2.
5.已知:x+y=5,(x-2)(y-2)=-3.
求下列代数式的的值.
(1)xy;
(2)x2+xy+5y;
(3)3x3y+6x2y2+3xy3.
解:(1)∵(x-2)(y-2)=-3,
∴xy-2(x+y)+4=-3,
∵x+y=5,∴xy=3.
(2)x2+xy+5y=x(x+y)+5y,
∵x+y=5,
∴原式=5x+5y=5(x+y)=5×5=25.
(3)3x3y+6x2y2+3xy3=3xy(x2+2xy+y2)=3xy(x+y)2,
当x+y=5,xy=3时,原式=3×3×52=225.
课堂小结
肆
课堂小结
1.本节课你学到了哪些知识?
2.你还有哪些疑问?
3.你在因式分解方面有哪些收获和体会?
课后作业
基础题:1.课后复习题 第 3,4,5题。
提高题:2.请学有余力的同学完成课后复习题第7题
谢
谢
同课章节目录
