第17章 因式分解 数学活动课件(共26张PPT) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 第17章 因式分解 数学活动课件(共26张PPT) 2025-2026学年数学人教版八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 23:29:59 | ||
图片预览








文档简介
(共26张PPT)
第17章 因式分解
数学活动
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
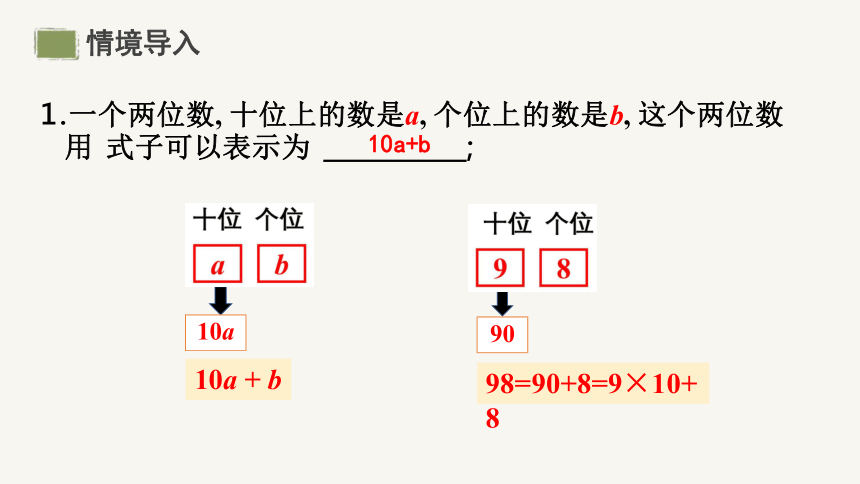
1.一个两位数, 十位上的数是a, 个位上的数是b, 这个两位数用 式子可以表示为 ;
98=90+8=9×10+8
90
10a + b
10a
10a+b
2.一个三位数,百位上的数是a ,十位上的数是b,个位上的数 是c,这个三位数用式子可以表示为 .
100a+10b+c
985=900+80+5=9×100+8×10+5
100a
10b
900
80
100a + 10b + c
小敏同学在数学课外活动中发现了一个有趣的数字运算规律:1×1=1;11×11=121;111×111=12321,…,其实在数字运算中还有许多规律性结论,这节课我们共同探讨数字运算中的某些规律.
新知初探
贰
新知初探
活动1
个位数字是5的两位数平方的规律
观察上述每一个算式,这些算式左右两侧具有什么样的规律?
问题1 我们共同来进行一个简单的数学计算:
15×15 =
25×25 =
35×35 =
……
1×2×100+25
2×3×100+25
3×4×100+25
15×15 =1×2×100+25 ;
25×25 =2×3×100+25 ;
35×35 =3×4×100+25 .
你能用语言表述出你发现的规律吗?
原十位上的数字加上1,再与自己相乘得到的结果乘100 ,再加上25,就是个位数字为5的两位数的平方数的结果.
归纳总结
问题3 用字母怎么表示得到的一般性的规律呢?
问题2 你能再举几个具有这样特征的例子,并用上述方法验证其正确性吗?
45×45 =2025=4×5×100+25
55×55 =3025=5×6×100+25
(10a+5)(10a+5) =100a(a+1)+25
问题4 你能用本章所学的知识证明你的结论吗?
证明:设两位数的十位数字为a,个位数字为5,则这个两位数可表示为10a +5.
所以 (10a+5)(10a+5)
=(10a+5)2
=100a2+100a +25
=100a(a+1)+25.
规律:
个位数是5的两位数的平方,结果的十位个位是25, 结果的千位百位是原十位上的数乘以比它大1的数的乘积.
(10a+5)2=a(a+1)·100+25
结果的十位个位是25 .
结果的千位百位是 原十位上的数乘以比 它大1的数的乘积.
小结:特殊算式—寻找规律—字母表示—推理证明.
活动2
利用因式分解生成密码
人类历史使用密码的历史悠久,利用因式分解可以生成密码;
(1)先将确定的多项式分解因式;
(2)再对因式赋值生成正整数或0的因式码;
(3)将因式码按从小到大的顺序排列就可以形成密码.
例如多项式x2y-4y.
(1) 分解因式,得x2y-4y=y(x2-4)=y(x+2)(x-2).
(2)若取x=15,y=12,则有
y=12, x+2=17,x-2=13.
所以12,17,13分别为因式码,
(3)将这三个因式码按从小到大的顺序排列,
所以密码为121317.
问题1 已知多项式16p4-q4,当取p=10,q=5时,
用上述方法生成的密码是什么
16p4-q4=(4p2)2-(q2)2
=(4p2+q2)(4p2-q2)
=(4p2+q2)(2p+q)(2p-q).
把p=10,q=5代入,得4p2+q2=4×102+52=425,
2p+q=2×10+5=25,2p-q=2×10-5=15.
将因式码按从小到大的顺序排列15, 25, 425.
因此,密码为 1525425.
问题2 已知多项式16p4-q4,用上述方法生成密码,
若密码的前两个因式码为5,15,你能求出第三个因式码吗
16p4-q4=(4p2)2-(q2)2=(4p2+q2)(4p2-q2)=(4p2+q2)(2p+q)(2p-q).
所以因式码为4p2+q2,2p+q,2p-q.
因为p,q为非负整数,所以2p-q<2p+q<4p2+q2.
因为密码的前两个因式码为5,15,
所以4p2+q2=4×52+52=125.
所以第三个因式码为125.
所以 解得
问题3 自己写一个多项式,并用上述方法生成密码.
例如多项式xy2-x,分解因式得xy2-x=x(y+1)(y-1).
取x=3,y=5,代入,得y+1=6,y-1=4.
所以因式码为3,6,4.
按由小到大的顺序排列:3,4,6.所以密码为346.
当堂达标
叁
当堂达标
1. 老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:32-12=8×1;52-32=8×2;72-52=8×3;…
(1)试写出符合上述规律的第五个算式;
解:(1)第五个算式为112-92=8×5.
解:(2)验证:设两个连续奇数为2n+1,2n-1,
则(2n+1)2-(2n-1)2
=(2n+1-2n+1)(2n+1+2n-1)
=2×4n
=8n.
故两个连续奇数的平方差是8的倍数.
2.(2)验证:设两个连续奇数为2n+1,2n-1
(其中n为正整数),用因式分解的方法说明它们的平方差是8的倍数.
2.在现今信息化时代,,锁屏密码为保护我们个人隐私起到
了不可或缺的作用,而诸如“1234”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式;x2-9因式分解的结果为(x-3)(x+3)或(x+3)(x-3),取个人年龄作为x的值,当x=13时,x-3=10,x+3=16,此时可以得到数字密码1016或1610.
(1)根据上述方法,若多项式为x2-16,当x=15时,求出锁屏密码;
解:(1)∵x2-16因式分解的结果为
(x-4)(x+4)或(x+4)(x-4),
∴当x=15时,x-4=11,x+4=19,
∴锁屏密码为1119或1911.
2.(2)若王老师选取的多项式为x3-x,已知王
老师手机的锁屏密码是6位数字353334,请尝试分析王老师当前年龄是多少岁,并说明理由.
解:(2)王老师的年龄是34岁.理由如下:
x3-x
=x(x2-1)
=x(x+1)(x-1)
∵王老师手机的锁屏密码是6位数字353334,35>34>33,
∴x+1=35,x=34,x-1=33,
∴x=34,
∴王老师的年龄是34岁.
课堂小结
肆
课堂小结
1.通过本节课的学习,你有那些收获
2.有什么体会和感悟
3.你还有哪些疑问
课后作业
基础题:1.课后复习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后复习题第8题
谢
谢
第17章 因式分解
数学活动
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
1.一个两位数, 十位上的数是a, 个位上的数是b, 这个两位数用 式子可以表示为 ;
98=90+8=9×10+8
90
10a + b
10a
10a+b
2.一个三位数,百位上的数是a ,十位上的数是b,个位上的数 是c,这个三位数用式子可以表示为 .
100a+10b+c
985=900+80+5=9×100+8×10+5
100a
10b
900
80
100a + 10b + c
小敏同学在数学课外活动中发现了一个有趣的数字运算规律:1×1=1;11×11=121;111×111=12321,…,其实在数字运算中还有许多规律性结论,这节课我们共同探讨数字运算中的某些规律.
新知初探
贰
新知初探
活动1
个位数字是5的两位数平方的规律
观察上述每一个算式,这些算式左右两侧具有什么样的规律?
问题1 我们共同来进行一个简单的数学计算:
15×15 =
25×25 =
35×35 =
……
1×2×100+25
2×3×100+25
3×4×100+25
15×15 =1×2×100+25 ;
25×25 =2×3×100+25 ;
35×35 =3×4×100+25 .
你能用语言表述出你发现的规律吗?
原十位上的数字加上1,再与自己相乘得到的结果乘100 ,再加上25,就是个位数字为5的两位数的平方数的结果.
归纳总结
问题3 用字母怎么表示得到的一般性的规律呢?
问题2 你能再举几个具有这样特征的例子,并用上述方法验证其正确性吗?
45×45 =2025=4×5×100+25
55×55 =3025=5×6×100+25
(10a+5)(10a+5) =100a(a+1)+25
问题4 你能用本章所学的知识证明你的结论吗?
证明:设两位数的十位数字为a,个位数字为5,则这个两位数可表示为10a +5.
所以 (10a+5)(10a+5)
=(10a+5)2
=100a2+100a +25
=100a(a+1)+25.
规律:
个位数是5的两位数的平方,结果的十位个位是25, 结果的千位百位是原十位上的数乘以比它大1的数的乘积.
(10a+5)2=a(a+1)·100+25
结果的十位个位是25 .
结果的千位百位是 原十位上的数乘以比 它大1的数的乘积.
小结:特殊算式—寻找规律—字母表示—推理证明.
活动2
利用因式分解生成密码
人类历史使用密码的历史悠久,利用因式分解可以生成密码;
(1)先将确定的多项式分解因式;
(2)再对因式赋值生成正整数或0的因式码;
(3)将因式码按从小到大的顺序排列就可以形成密码.
例如多项式x2y-4y.
(1) 分解因式,得x2y-4y=y(x2-4)=y(x+2)(x-2).
(2)若取x=15,y=12,则有
y=12, x+2=17,x-2=13.
所以12,17,13分别为因式码,
(3)将这三个因式码按从小到大的顺序排列,
所以密码为121317.
问题1 已知多项式16p4-q4,当取p=10,q=5时,
用上述方法生成的密码是什么
16p4-q4=(4p2)2-(q2)2
=(4p2+q2)(4p2-q2)
=(4p2+q2)(2p+q)(2p-q).
把p=10,q=5代入,得4p2+q2=4×102+52=425,
2p+q=2×10+5=25,2p-q=2×10-5=15.
将因式码按从小到大的顺序排列15, 25, 425.
因此,密码为 1525425.
问题2 已知多项式16p4-q4,用上述方法生成密码,
若密码的前两个因式码为5,15,你能求出第三个因式码吗
16p4-q4=(4p2)2-(q2)2=(4p2+q2)(4p2-q2)=(4p2+q2)(2p+q)(2p-q).
所以因式码为4p2+q2,2p+q,2p-q.
因为p,q为非负整数,所以2p-q<2p+q<4p2+q2.
因为密码的前两个因式码为5,15,
所以4p2+q2=4×52+52=125.
所以第三个因式码为125.
所以 解得
问题3 自己写一个多项式,并用上述方法生成密码.
例如多项式xy2-x,分解因式得xy2-x=x(y+1)(y-1).
取x=3,y=5,代入,得y+1=6,y-1=4.
所以因式码为3,6,4.
按由小到大的顺序排列:3,4,6.所以密码为346.
当堂达标
叁
当堂达标
1. 老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:32-12=8×1;52-32=8×2;72-52=8×3;…
(1)试写出符合上述规律的第五个算式;
解:(1)第五个算式为112-92=8×5.
解:(2)验证:设两个连续奇数为2n+1,2n-1,
则(2n+1)2-(2n-1)2
=(2n+1-2n+1)(2n+1+2n-1)
=2×4n
=8n.
故两个连续奇数的平方差是8的倍数.
2.(2)验证:设两个连续奇数为2n+1,2n-1
(其中n为正整数),用因式分解的方法说明它们的平方差是8的倍数.
2.在现今信息化时代,,锁屏密码为保护我们个人隐私起到
了不可或缺的作用,而诸如“1234”、生日等简单密码又容易被破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式;x2-9因式分解的结果为(x-3)(x+3)或(x+3)(x-3),取个人年龄作为x的值,当x=13时,x-3=10,x+3=16,此时可以得到数字密码1016或1610.
(1)根据上述方法,若多项式为x2-16,当x=15时,求出锁屏密码;
解:(1)∵x2-16因式分解的结果为
(x-4)(x+4)或(x+4)(x-4),
∴当x=15时,x-4=11,x+4=19,
∴锁屏密码为1119或1911.
2.(2)若王老师选取的多项式为x3-x,已知王
老师手机的锁屏密码是6位数字353334,请尝试分析王老师当前年龄是多少岁,并说明理由.
解:(2)王老师的年龄是34岁.理由如下:
x3-x
=x(x2-1)
=x(x+1)(x-1)
∵王老师手机的锁屏密码是6位数字353334,35>34>33,
∴x+1=35,x=34,x-1=33,
∴x=34,
∴王老师的年龄是34岁.
课堂小结
肆
课堂小结
1.通过本节课的学习,你有那些收获
2.有什么体会和感悟
3.你还有哪些疑问
课后作业
基础题:1.课后复习题 第 1,2,3题。
提高题:2.请学有余力的同学完成课后复习题第8题
谢
谢
同课章节目录
