期中综合评价卷 (含答案) 2025-2026学年数学人教版八年级上册
文档属性
| 名称 | 期中综合评价卷 (含答案) 2025-2026学年数学人教版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 00:00:00 | ||
图片预览





文档简介
期中综合评价卷
时间:120分钟 满分:120分
班级: 学号: 姓名: 成绩:
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
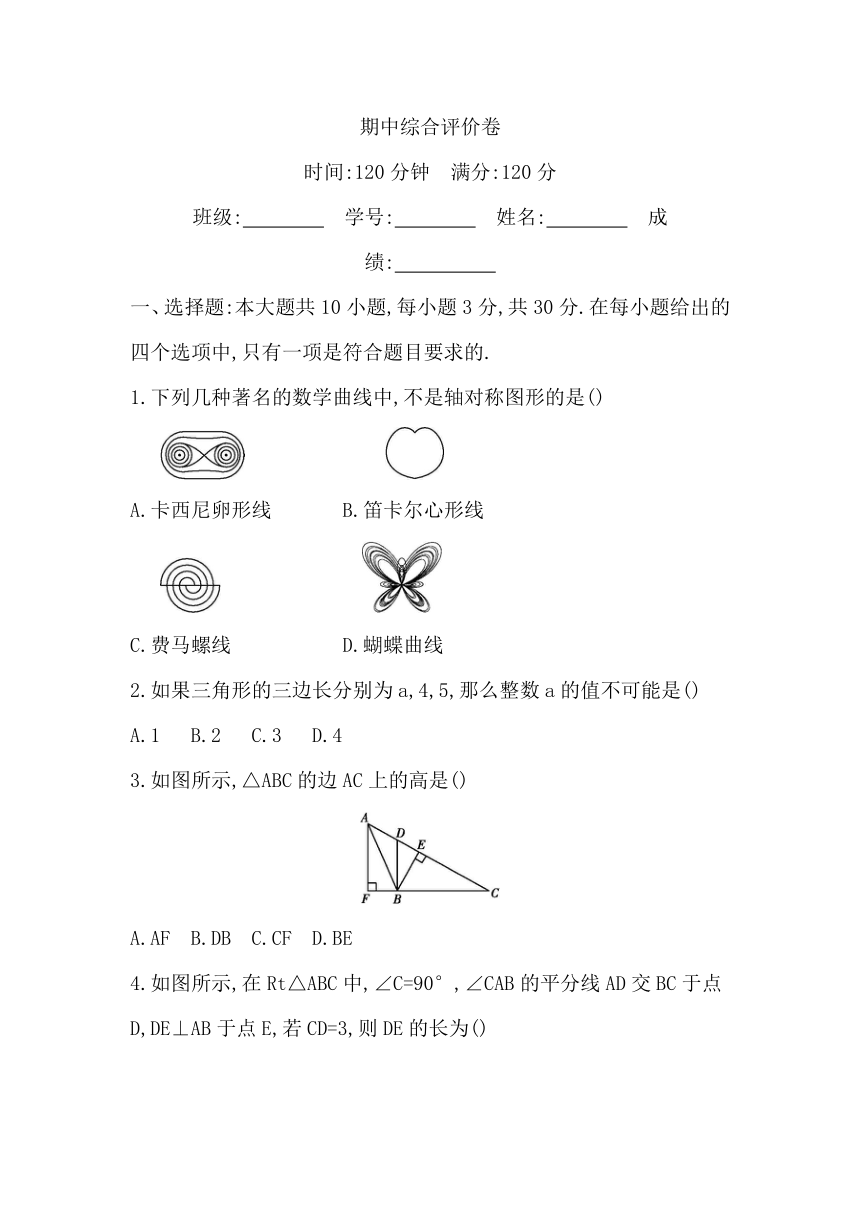
1.下列几种著名的数学曲线中,不是轴对称图形的是()
A.卡西尼卵形线 B.笛卡尔心形线
C.费马螺线 D.蝴蝶曲线
2.如果三角形的三边长分别为a,4,5,那么整数a的值不可能是()
A.1 B.2 C.3 D.4
3.如图所示,△ABC的边AC上的高是()
A.AF B.DB C.CF D.BE
4.如图所示,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=3,则DE的长为()
A.2 B.3 C.4 D.5
5.如图所示,AD是△ABC的中线,点E为AD的中点,连接CE,若△ABC的面积为12 cm2,则△CDE的面积为()
A.3 cm2 B.5 cm2 C.4 cm2 D.6 cm2
6.如图所示,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌
△ADE的是()
A.∠B=∠D B.BC=DE C.∠1=∠2 D.AB=AD
7.若点A(m-3,4)与点B(2,n+6)关于y轴对称,则m-n的值为()
A.3 B.7 C.11 D.15
8.如图所示,在△CEF中,∠E=78°,∠F=47°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()
A.45° B.47° C.55° D.78°
9.已知a,b是等腰三角形的两边长,且a,b满足|a-2|+(b-3)2=0,则此等腰三角形的周长为()
A.7 B.8
C.6或8 D.7或8
10.如图所示,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF.以下结论:①AD∥BC;②∠DAC=2∠ADB;③
∠ADC=90°-∠ABD;④DB平分∠ADC.其中正确的结论有()
A.4个 B.3个 C.2个 D.1个
二、填空题:本大题共5小题,每小题3分,共15分.
11.椅子是一种日常生活家具,现代的椅子追求美观时尚,在如图所示的椅子的设计中,将椅子脚设计成三角形,椅子非常稳固,其所利用的数学原理是 .
12.如图所示,AB的垂直平分线分别交AB,AC于点D,E.若AC=18,AE∶EC=2∶1,则BE的长为 .
13.如图所示,在△ABC中,AB=AC,D为BC边的中点,∠B=40°,则
∠CAD= °.
14.如图所示,点A,B,C,D均在正方形网格格点上,则 ∠ABC+∠ADC=
.
15.如图所示,在△ABC中,AB=AC=10,BC=12,AD=8,AD,BE分别是△ABC边BC,AC上的高,P是AD上的动点,则PE+PC的最小值是 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.已知a,b,c是三角形的三边长,化简|a-b+c|-|a-b-c|.
17.如图所示,在△ABC中,D是BC的中点,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.求证:BE=CF.
18.如图所示,某海监船在海域A处巡逻,观测到岛礁B在北偏东60°方向,该船以每小时10 n mile的速度向正东方向航行到C处,观测岛礁B在北偏东30°方向,继续以相同的速度向正东方向航行到D处时,再观测到岛礁B在北偏西30°方向,当海监船到达C处时恰与岛礁B相距 20 n mile,请你分别确定该海监船从A处到达C处和D处所用的时间.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图所示,在△ABC中,AB=AC,BE⊥AC于点E,且D,E分别是AB,AC的中点,延长BC至点F,使CF=CE.
(1)求∠ABC的度数.
(2)求证:BE=FE.
20.如图所示,OD平分∠AOB,点P为OA上一点.
(1)尺规作图:以P为顶点,作∠APQ=∠AOB,交OD于点Q(不写作法,保留作图痕迹);
(2)在(1)的条件下,若∠AOB=60°,求∠DQP的度数.
21.综合与实践.
【背景】有一副三角板和一条直线MN,已知∠CAB=∠AED=90°,∠C=
45°,∠EAD=30°.
【操作】如图(1)所示,将三角板ABC和三角板ADE的顶点A重叠摆放在直线MN上,且三角板ADE始终摆放在直线MN下方,三角板ABC可绕点A任意旋转.
【假设】设∠BAN=m°,∠DAN=n°(0≤m≤180,0≤n≤150).
【问题】(1)当m+n=0时,求∠CAE的度数;
(2)当点C,A,E三点在一条直线上时,点A,C,E的位置如图(2)所示,请说明m与n的数量关系.
五、解答题(三):本大题共2小题,第22题13分,第23题 14分,共27分.
22.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】(1)如图(1)所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,∠AEB= .
(2)如图(2)所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗 如果不会,求∠D的度数;如果会,请说明理由;
【问题拓展】
(3)在图(2)的基础上,如果∠MON=α,其余条件不变,随着点A,B的运动[如图(3)所示],求∠D的度数.(用含α的代数式表示)
23.在等边三角形ABC的两边AB,AC所在直线上分别有两点M,N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M,N分别在直线AB,AC上移动时,BM,NC,MN之间的数量关系及△AMN的周长Q与等边三角形ABC的周长L的关系.
(1)如图(1)所示,当点M,N在边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系是 ;此时= .
(2)如图(2)所示,点M,N在边AB,AC上,且当DM≠DN时,猜想第(1)问的两个结论还成立吗 若成立请给予证明;若不成立,请说明理由.
(3)如图(3)所示,当M,N分别在边AB,CA的延长线上时,探索BM,NC,MN之间的数量关系如何 并给出证明.
期中综合评价卷
1.C 2.A 3.D 4.B 5.A 6.D 7.A 8.C 9.D 10.B
11.三角形的稳定性 12.12 13.50 14.45° 15.9.6
16.解:原式=2a-2b.
17.证明:∵D是BC的中点,∴BD=CD.
∵CF∥AB交ED的延长线于点F,∴∠BED=∠F.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).∴BE=CF.
18.解:船从A处到达C处所用的时间为2 h,
船从A处到达D处所用的时间为4 h.
19.(1)解:∠ABC的度数为60°.
(2)证明:∵CF=CE,∴∠F=∠CEF.
∵∠ACB=60°=∠F+∠CEF,∴∠F=30°.
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°.∴∠F=∠EBC.∴BE=FE.
20.解:(1)如图所示,∠APQ即为所作的角.
(2)∠DQP的度数为150°.
21.解:(1)∵∠CAB=∠AED=90°,∠EAD=30°,
∠BAN=m°,∠DAN=n°(0≤m≤180,0≤n≤150),
∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴当m+n=0时,∠CAE=90°+30°=120°.
(2)∵C,A,E三点在一条直线上,∴∠CAE=180°.
∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴180=90+m+n+30.∴m+n=60.
22.解:(1)135°
(2)①45 ②∠D的度数不随A,B的运动而发生变化.
设∠BAD=x,
∵AD平分∠BAO,∴∠BAO=2x.
∵∠AOB=90°,
∴∠ABN=∠AOB+∠BAO=90°+2x.
∵BC平分∠ABN,∴∠ABC=45°+x.
∵∠ABC=∠D+∠BAD,
∴∠D=∠ABC-∠BAD=45°+x-x=45°.
(3)设∠BAD=x,
∵AD平分∠BAO,∴∠BAO=2x.
∵∠AOB=α,
∴∠ABN=∠AOB+∠BAO=α+2x.
∵BC平分∠ABN,∴∠ABC=α+x.
∵∠ABC=∠D+∠BAD,
∴∠D=∠ABC-∠BAD=α+x-x=α.
23.解:(1)BM+NC=MN
(2)猜想:结论仍然成立.
证明如下:如图①所示,在NC的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠M1CD=90°,
BD=CD,
∴△DBM≌△DCM1.
∴DM=DM1,∠MDB=∠M1DC,M1C=BM.
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°.
∴△MDN≌△M1DN.
∴MN=M1N=M1C+NC=BM+NC.
∴△AMN的周长为
AM+MN+AN=AM+BM+CN+AN=AB+AC.
∴=.
(3)NC-BM=MN.
证明如下:如图②所示,在CN上截取CM1=BM,连接DM1,
可证△DBM≌△DCM1,
∴DM=DM1,∠MDB=∠M1DC.
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN.
∴MN=M1N.
∴NC-BM=MN.
时间:120分钟 满分:120分
班级: 学号: 姓名: 成绩:
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列几种著名的数学曲线中,不是轴对称图形的是()
A.卡西尼卵形线 B.笛卡尔心形线
C.费马螺线 D.蝴蝶曲线
2.如果三角形的三边长分别为a,4,5,那么整数a的值不可能是()
A.1 B.2 C.3 D.4
3.如图所示,△ABC的边AC上的高是()
A.AF B.DB C.CF D.BE
4.如图所示,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,DE⊥AB于点E,若CD=3,则DE的长为()
A.2 B.3 C.4 D.5
5.如图所示,AD是△ABC的中线,点E为AD的中点,连接CE,若△ABC的面积为12 cm2,则△CDE的面积为()
A.3 cm2 B.5 cm2 C.4 cm2 D.6 cm2
6.如图所示,已知AE=AC,∠C=∠E,下列条件中,无法判定△ABC≌
△ADE的是()
A.∠B=∠D B.BC=DE C.∠1=∠2 D.AB=AD
7.若点A(m-3,4)与点B(2,n+6)关于y轴对称,则m-n的值为()
A.3 B.7 C.11 D.15
8.如图所示,在△CEF中,∠E=78°,∠F=47°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是()
A.45° B.47° C.55° D.78°
9.已知a,b是等腰三角形的两边长,且a,b满足|a-2|+(b-3)2=0,则此等腰三角形的周长为()
A.7 B.8
C.6或8 D.7或8
10.如图所示,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF.以下结论:①AD∥BC;②∠DAC=2∠ADB;③
∠ADC=90°-∠ABD;④DB平分∠ADC.其中正确的结论有()
A.4个 B.3个 C.2个 D.1个
二、填空题:本大题共5小题,每小题3分,共15分.
11.椅子是一种日常生活家具,现代的椅子追求美观时尚,在如图所示的椅子的设计中,将椅子脚设计成三角形,椅子非常稳固,其所利用的数学原理是 .
12.如图所示,AB的垂直平分线分别交AB,AC于点D,E.若AC=18,AE∶EC=2∶1,则BE的长为 .
13.如图所示,在△ABC中,AB=AC,D为BC边的中点,∠B=40°,则
∠CAD= °.
14.如图所示,点A,B,C,D均在正方形网格格点上,则 ∠ABC+∠ADC=
.
15.如图所示,在△ABC中,AB=AC=10,BC=12,AD=8,AD,BE分别是△ABC边BC,AC上的高,P是AD上的动点,则PE+PC的最小值是 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.已知a,b,c是三角形的三边长,化简|a-b+c|-|a-b-c|.
17.如图所示,在△ABC中,D是BC的中点,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.求证:BE=CF.
18.如图所示,某海监船在海域A处巡逻,观测到岛礁B在北偏东60°方向,该船以每小时10 n mile的速度向正东方向航行到C处,观测岛礁B在北偏东30°方向,继续以相同的速度向正东方向航行到D处时,再观测到岛礁B在北偏西30°方向,当海监船到达C处时恰与岛礁B相距 20 n mile,请你分别确定该海监船从A处到达C处和D处所用的时间.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图所示,在△ABC中,AB=AC,BE⊥AC于点E,且D,E分别是AB,AC的中点,延长BC至点F,使CF=CE.
(1)求∠ABC的度数.
(2)求证:BE=FE.
20.如图所示,OD平分∠AOB,点P为OA上一点.
(1)尺规作图:以P为顶点,作∠APQ=∠AOB,交OD于点Q(不写作法,保留作图痕迹);
(2)在(1)的条件下,若∠AOB=60°,求∠DQP的度数.
21.综合与实践.
【背景】有一副三角板和一条直线MN,已知∠CAB=∠AED=90°,∠C=
45°,∠EAD=30°.
【操作】如图(1)所示,将三角板ABC和三角板ADE的顶点A重叠摆放在直线MN上,且三角板ADE始终摆放在直线MN下方,三角板ABC可绕点A任意旋转.
【假设】设∠BAN=m°,∠DAN=n°(0≤m≤180,0≤n≤150).
【问题】(1)当m+n=0时,求∠CAE的度数;
(2)当点C,A,E三点在一条直线上时,点A,C,E的位置如图(2)所示,请说明m与n的数量关系.
五、解答题(三):本大题共2小题,第22题13分,第23题 14分,共27分.
22.【问题背景】∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
【问题思考】(1)如图(1)所示,AE,BE分别是∠BAO和∠ABO的平分线,随着点A,B的运动,∠AEB= .
(2)如图(2)所示,若BC是∠ABN的平分线,BC的反向延长线与∠OAB的平分线交于点D.
①若∠BAO=70°,则∠D= °.
②随着点A,B的运动,∠D的大小会变吗 如果不会,求∠D的度数;如果会,请说明理由;
【问题拓展】
(3)在图(2)的基础上,如果∠MON=α,其余条件不变,随着点A,B的运动[如图(3)所示],求∠D的度数.(用含α的代数式表示)
23.在等边三角形ABC的两边AB,AC所在直线上分别有两点M,N,D为△ABC外一点,且∠MDN=60°,∠BDC=120°,BD=DC.探究:当M,N分别在直线AB,AC上移动时,BM,NC,MN之间的数量关系及△AMN的周长Q与等边三角形ABC的周长L的关系.
(1)如图(1)所示,当点M,N在边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系是 ;此时= .
(2)如图(2)所示,点M,N在边AB,AC上,且当DM≠DN时,猜想第(1)问的两个结论还成立吗 若成立请给予证明;若不成立,请说明理由.
(3)如图(3)所示,当M,N分别在边AB,CA的延长线上时,探索BM,NC,MN之间的数量关系如何 并给出证明.
期中综合评价卷
1.C 2.A 3.D 4.B 5.A 6.D 7.A 8.C 9.D 10.B
11.三角形的稳定性 12.12 13.50 14.45° 15.9.6
16.解:原式=2a-2b.
17.证明:∵D是BC的中点,∴BD=CD.
∵CF∥AB交ED的延长线于点F,∴∠BED=∠F.
在△BDE和△CDF中,
∴△BDE≌△CDF(AAS).∴BE=CF.
18.解:船从A处到达C处所用的时间为2 h,
船从A处到达D处所用的时间为4 h.
19.(1)解:∠ABC的度数为60°.
(2)证明:∵CF=CE,∴∠F=∠CEF.
∵∠ACB=60°=∠F+∠CEF,∴∠F=30°.
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=30°.∴∠F=∠EBC.∴BE=FE.
20.解:(1)如图所示,∠APQ即为所作的角.
(2)∠DQP的度数为150°.
21.解:(1)∵∠CAB=∠AED=90°,∠EAD=30°,
∠BAN=m°,∠DAN=n°(0≤m≤180,0≤n≤150),
∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴当m+n=0时,∠CAE=90°+30°=120°.
(2)∵C,A,E三点在一条直线上,∴∠CAE=180°.
∵∠CAE=∠CAB+∠BAN+∠DAN+∠EAD,
∴180=90+m+n+30.∴m+n=60.
22.解:(1)135°
(2)①45 ②∠D的度数不随A,B的运动而发生变化.
设∠BAD=x,
∵AD平分∠BAO,∴∠BAO=2x.
∵∠AOB=90°,
∴∠ABN=∠AOB+∠BAO=90°+2x.
∵BC平分∠ABN,∴∠ABC=45°+x.
∵∠ABC=∠D+∠BAD,
∴∠D=∠ABC-∠BAD=45°+x-x=45°.
(3)设∠BAD=x,
∵AD平分∠BAO,∴∠BAO=2x.
∵∠AOB=α,
∴∠ABN=∠AOB+∠BAO=α+2x.
∵BC平分∠ABN,∴∠ABC=α+x.
∵∠ABC=∠D+∠BAD,
∴∠D=∠ABC-∠BAD=α+x-x=α.
23.解:(1)BM+NC=MN
(2)猜想:结论仍然成立.
证明如下:如图①所示,在NC的延长线上截取CM1=BM,连接DM1,
∵∠MBD=∠M1CD=90°,
BD=CD,
∴△DBM≌△DCM1.
∴DM=DM1,∠MDB=∠M1DC,M1C=BM.
∵∠MDN=60°,∠BDC=120°,
∴∠M1DN=∠MDN=60°.
∴△MDN≌△M1DN.
∴MN=M1N=M1C+NC=BM+NC.
∴△AMN的周长为
AM+MN+AN=AM+BM+CN+AN=AB+AC.
∴=.
(3)NC-BM=MN.
证明如下:如图②所示,在CN上截取CM1=BM,连接DM1,
可证△DBM≌△DCM1,
∴DM=DM1,∠MDB=∠M1DC.
可证∠M1DN=∠MDN=60°,
∴△MDN≌△M1DN.
∴MN=M1N.
∴NC-BM=MN.
同课章节目录
