2.1 函数的概念 课件 (2)
图片预览






文档简介
课件22张PPT。2.1函数的概念 设在一个变化过程中有两个变量x与y, 如果对于x的每一个值, y都有惟一的值与它对应, 那么就说 y是 x的函数, x叫做自变量,y叫因变量.
我们在初中学习函数的概念,它是如何定义的?在初中已经学过哪些函数?其解析式分别是什么? 一次函数
二次函数
正比例函数
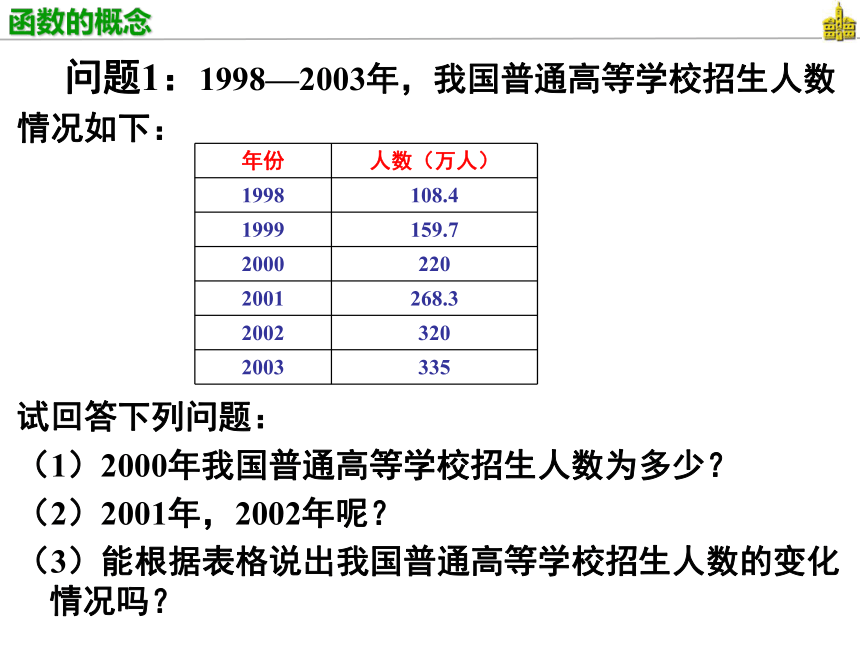
反比例函数 我们一些具体的函数,那么为什么还要学习函数呢?请同学们思考下面的两个问题:?仅用上述函数概念很难回答这些问题,我们需要从新的角度来认识函数的概念,这就是 我们今天学习的课题—函数的概念 问题1:1998—2003年,我国普通高等学校招生人数
情况如下:
试回答下列问题:
(1)2000年我国普通高等学校招生人数为多少?
(2)2001年,2002年呢?
(3)能根据表格说出我国普通高等学校招生人数的变化情况吗? 问题2:一物体在490米高的位置从静止开始下落,
下落的距离y(m)与下落时间x(s)之间近似地满足关
系式y=4.9x2.
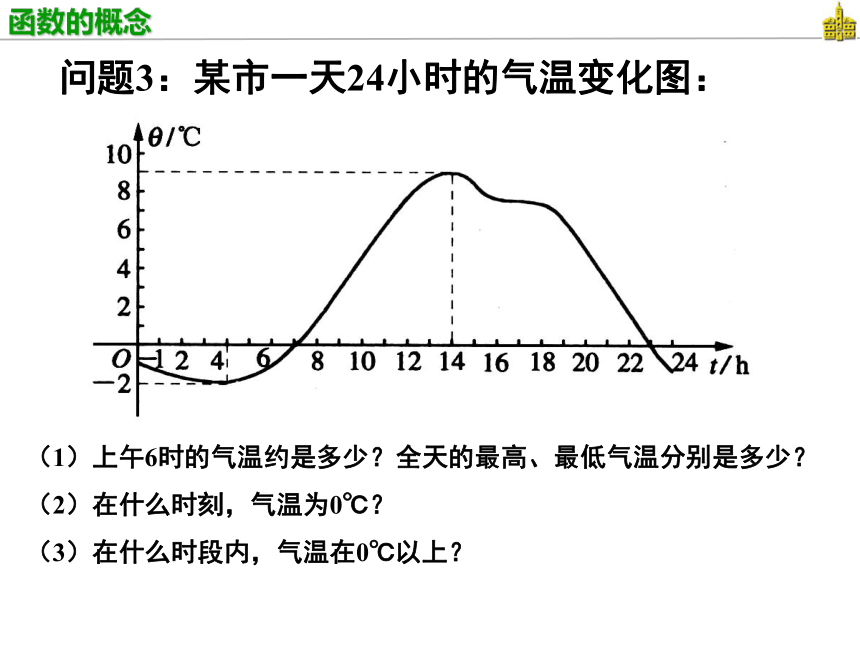
若一物体下落2s,你能求出下落的距离吗?问题3:某市一天24小时的气温变化图:(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0℃?
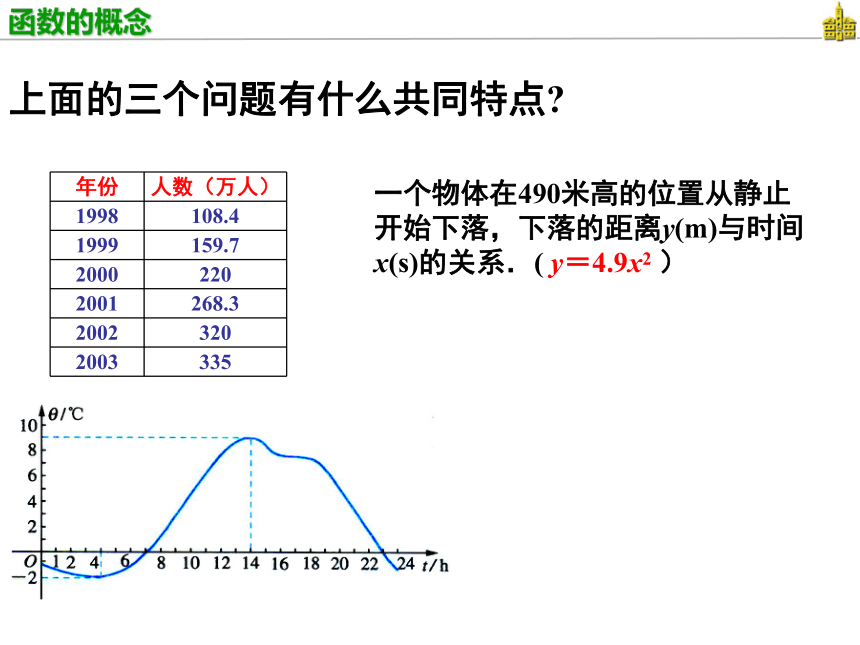
(3)在什么时段内,气温在0℃以上?一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )上面的三个问题有什么共同特点?
在上述的每一个问题中都含有两个变
量,当一个变量的取值确定后,另一个变
量的值随之惟一确定,每一个问题确定了
一个函数关系. 一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )能否用集合语言来阐述这三个问题的共同特点?以问题1为例,年份设为集合A,人数设为集合B,两个集合的对应关系为199819992000200120022003108.4159.7220268.3320335(1)会不会出现某个年份没 有与之对应的人数?
(2)会不会出现某个年份有两个人数与之对应?AB{1998,1999 ,2000,2001,2002,2003}{108.4,159.7,220,268.3,320,335}非空数集A非空数集B一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )对于集合A中的每一个元素 x,在集合B中都有惟一的元素 y 和它对应,
记作: f:A→B{x|0≤x≤10}{y|0≤y≤490}{x|0≤x≤24}{t|-2≤t≤9} 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数
记作: y=f (x),x?A1. 定义 其中,x叫做自变量,x的取值范围A叫做函数的定义域;设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,
记作: y=f (x),x?A
定义域A;
值域{f(x)|x∈R};;
对应法则f.3. 函数的三要素: 例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.(1)(4)(3)(2)例1 判断下列对应是否为函数????例2 求下列函数的定义域.?课堂小结1.函数的概念;构成函数的三要素;
2.区间的表示方法.谢谢大家!
我们在初中学习函数的概念,它是如何定义的?在初中已经学过哪些函数?其解析式分别是什么? 一次函数
二次函数
正比例函数
反比例函数 我们一些具体的函数,那么为什么还要学习函数呢?请同学们思考下面的两个问题:?仅用上述函数概念很难回答这些问题,我们需要从新的角度来认识函数的概念,这就是 我们今天学习的课题—函数的概念 问题1:1998—2003年,我国普通高等学校招生人数
情况如下:
试回答下列问题:
(1)2000年我国普通高等学校招生人数为多少?
(2)2001年,2002年呢?
(3)能根据表格说出我国普通高等学校招生人数的变化情况吗? 问题2:一物体在490米高的位置从静止开始下落,
下落的距离y(m)与下落时间x(s)之间近似地满足关
系式y=4.9x2.
若一物体下落2s,你能求出下落的距离吗?问题3:某市一天24小时的气温变化图:(1)上午6时的气温约是多少?全天的最高、最低气温分别是多少?
(2)在什么时刻,气温为0℃?
(3)在什么时段内,气温在0℃以上?一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )上面的三个问题有什么共同特点?
在上述的每一个问题中都含有两个变
量,当一个变量的取值确定后,另一个变
量的值随之惟一确定,每一个问题确定了
一个函数关系. 一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )能否用集合语言来阐述这三个问题的共同特点?以问题1为例,年份设为集合A,人数设为集合B,两个集合的对应关系为199819992000200120022003108.4159.7220268.3320335(1)会不会出现某个年份没 有与之对应的人数?
(2)会不会出现某个年份有两个人数与之对应?AB{1998,1999 ,2000,2001,2002,2003}{108.4,159.7,220,268.3,320,335}非空数集A非空数集B一个物体在490米高的位置从静止开始下落,下落的距离y(m)与时间x(s)的关系.( y=4.9x2 )对于集合A中的每一个元素 x,在集合B中都有惟一的元素 y 和它对应,
记作: f:A→B{x|0≤x≤10}{y|0≤y≤490}{x|0≤x≤24}{t|-2≤t≤9} 设A、B是非空的数集,如果按照某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一确定
的数 f(x)和它对应,那么就称f:A→B为
从集合A到集合B的一个函数
记作: y=f (x),x?A1. 定义 其中,x叫做自变量,x的取值范围A叫做函数的定义域;设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,
记作: y=f (x),x?A
定义域A;
值域{f(x)|x∈R};;
对应法则f.3. 函数的三要素: 例1.结合函数的定义,判断下列对应是不是从数
集A到数集B的函数.(1)(4)(3)(2)例1 判断下列对应是否为函数????例2 求下列函数的定义域.?课堂小结1.函数的概念;构成函数的三要素;
2.区间的表示方法.谢谢大家!
