2.1.1 函数的概念和图象 课件
图片预览





文档简介
(共13张PPT)
函数的概念和图象
(1)运动会前八名的得分情况
名次 1 2 3 4 5 6 7 8
分数 10 8 6 5 4 3 2 1
(2)汽车的行驶速度为80千米/小时,汽车行 驶的距离y与行驶时间x之间的关系式为:y=80x
(3)情景3:某市一天24小时内的气温变化图:(图略p21)
提问(1):这三个例子中都涉及到了几个变化的量?
提问(2):当其中一个变量取值确定后,另一个变量将如何?
提问(3):这样的关系在初中称之为什么?
提问(4):观察上述三问题,它们分别涉及到了哪些集合?
提问(5):两个集合的元素之间具有怎样的关系?
思考:如何用集合的语言来阐述上述三个问题的共同特征?
提问(4):观察上述三问题,它们分别涉及到了哪些集合?
(两个非空数集A,B)
提问(5):两个集合的元素之间具有怎样的关系?
(对应:对于A中任意元素x,B中总有一个元素y与之对应;或一个输入值对应唯一的输出值)
函数的有关概念
1.定义:一般地,设A,B是两个非空的数集,如果按某种对应法则f,对于集合A中的每一个元素x,在集合B中都有唯一的元素y和它对应,这样的对应叫做从A到B的一个函数
记作:y=f(x),x A
2.定义域:所有自变量x的值组成的集合A
3.值 域:所有因变量y的值组成的集合(或者所有函数值组成的集合)
函数概念的理解
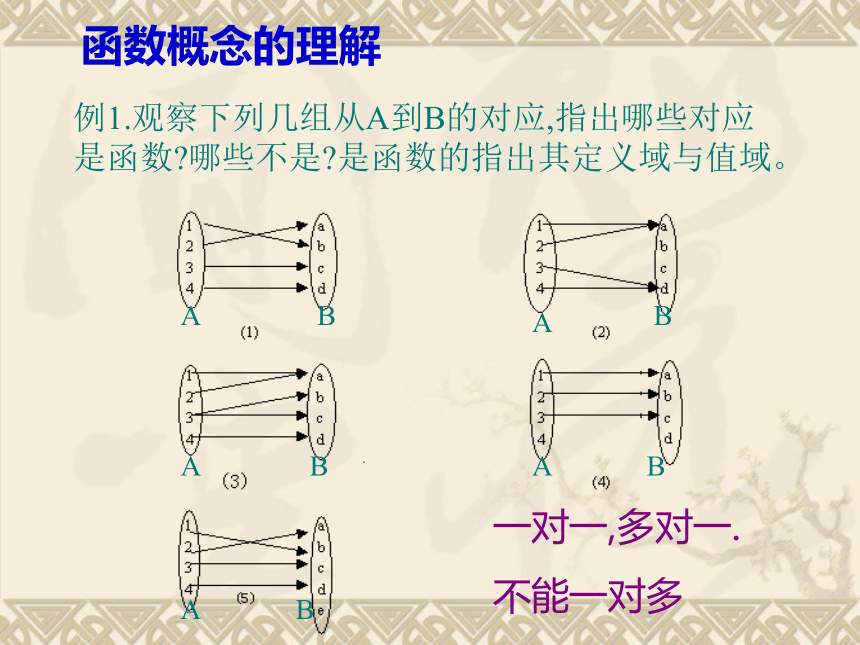
例1.观察下列几组从A到B的对应,指出哪些对应是函数 哪些不是 是函数的指出其定义域与值域。
A
B
A
B
A
B
A
B
A
B
一对一,多对一.
不能一对多
例2 判断下列对应是否为函数:
(1) x
(2) x y,其中
(3) x 1其中x R
(4) 已知集合A=R,B={-1,1},对应法则f:
当x为有理数时,f(x)=-1;当x为无理数时,f(x)=1,对应 f: A B
对 错 对 对
探求定义,提出注意
① A、B非空数集
③ 任意的x∈A,存在唯一的y∈B与之对应
②函数有三个要素;定义域、对应关系、值域
(当定义域和对应关系确定后,值域也确定了)
(一对一,多对一,不能“一对多”)
④f表示对应关系,在不同的函数中,f的具体含义不一样.
在研究函数时,除用符号f(x)表示函数外,还常用g(x) 、F(x)、G(x)等符号来表示
例3 下列两个函数是否表示同一个函数?
(1)
(2)
(4)
(3)
两个函数相同的条件是;两函数的三要素相同或者
两函数的定义域和对应法则相同
例4 求下列函数的定义域
(使式子有意义)
解(1)
函数定义域为{ }
(2)
函数定义域为{ }
例5.已知
例6.求下列函数的值域
1. 在下列图象中,哪些是函数图象,哪些不是
x
x
x
x
y
y
y
y
o
o
o
o
(1)
(2)
(3)
(4)
15分钟课堂练习
2.
3.求定义域
(1)
(2)
(3)
本课总结:
知识内容:
(1)函数的定义
(2)函数的三要素
(3)两函数相同的条件
(4)函数的定义域
函数的概念和图象
(1)运动会前八名的得分情况
名次 1 2 3 4 5 6 7 8
分数 10 8 6 5 4 3 2 1
(2)汽车的行驶速度为80千米/小时,汽车行 驶的距离y与行驶时间x之间的关系式为:y=80x
(3)情景3:某市一天24小时内的气温变化图:(图略p21)
提问(1):这三个例子中都涉及到了几个变化的量?
提问(2):当其中一个变量取值确定后,另一个变量将如何?
提问(3):这样的关系在初中称之为什么?
提问(4):观察上述三问题,它们分别涉及到了哪些集合?
提问(5):两个集合的元素之间具有怎样的关系?
思考:如何用集合的语言来阐述上述三个问题的共同特征?
提问(4):观察上述三问题,它们分别涉及到了哪些集合?
(两个非空数集A,B)
提问(5):两个集合的元素之间具有怎样的关系?
(对应:对于A中任意元素x,B中总有一个元素y与之对应;或一个输入值对应唯一的输出值)
函数的有关概念
1.定义:一般地,设A,B是两个非空的数集,如果按某种对应法则f,对于集合A中的每一个元素x,在集合B中都有唯一的元素y和它对应,这样的对应叫做从A到B的一个函数
记作:y=f(x),x A
2.定义域:所有自变量x的值组成的集合A
3.值 域:所有因变量y的值组成的集合(或者所有函数值组成的集合)
函数概念的理解
例1.观察下列几组从A到B的对应,指出哪些对应是函数 哪些不是 是函数的指出其定义域与值域。
A
B
A
B
A
B
A
B
A
B
一对一,多对一.
不能一对多
例2 判断下列对应是否为函数:
(1) x
(2) x y,其中
(3) x 1其中x R
(4) 已知集合A=R,B={-1,1},对应法则f:
当x为有理数时,f(x)=-1;当x为无理数时,f(x)=1,对应 f: A B
对 错 对 对
探求定义,提出注意
① A、B非空数集
③ 任意的x∈A,存在唯一的y∈B与之对应
②函数有三个要素;定义域、对应关系、值域
(当定义域和对应关系确定后,值域也确定了)
(一对一,多对一,不能“一对多”)
④f表示对应关系,在不同的函数中,f的具体含义不一样.
在研究函数时,除用符号f(x)表示函数外,还常用g(x) 、F(x)、G(x)等符号来表示
例3 下列两个函数是否表示同一个函数?
(1)
(2)
(4)
(3)
两个函数相同的条件是;两函数的三要素相同或者
两函数的定义域和对应法则相同
例4 求下列函数的定义域
(使式子有意义)
解(1)
函数定义域为{ }
(2)
函数定义域为{ }
例5.已知
例6.求下列函数的值域
1. 在下列图象中,哪些是函数图象,哪些不是
x
x
x
x
y
y
y
y
o
o
o
o
(1)
(2)
(3)
(4)
15分钟课堂练习
2.
3.求定义域
(1)
(2)
(3)
本课总结:
知识内容:
(1)函数的定义
(2)函数的三要素
(3)两函数相同的条件
(4)函数的定义域
