2.2.1 函数的单调性 课件

课件25张PPT。§2.2 函数的简单性质
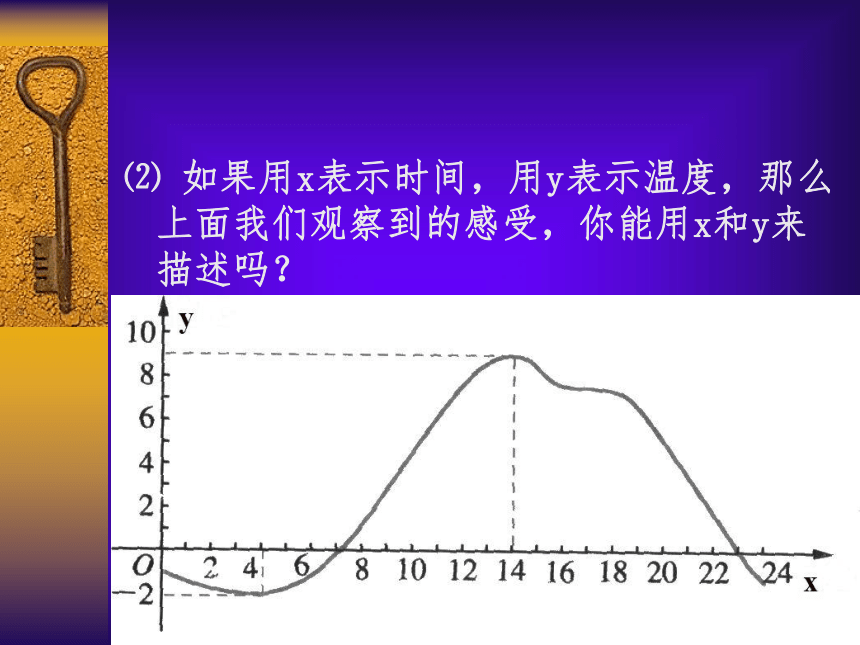
2.2.1 函数的单调性情境：下图是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数，记为θ＝ f (t) ，观察此函数的图像，你发现了哪些有用的信息？ 今天我们研究的重点是：函数图像的升高或下降。1.观察这个气温变化图，说说气温在哪些时间段内是逐渐升高的，在哪些时间段内是下降的？
2.怎样用数学的语言刻画上述时段的“随着时间的推移气温逐渐升高”这一特征？
启发诱导⑴ 从左向右看，实际是自变量t从小变到大，我们观察到的函数θ是如何变化的？
⑵ 如果用x表示时间，用y表示温度，那么上面我们观察到的感受，你能用x和y来描述吗？当x∈【4, 14】时，随着时间x的增大，气温y逐渐升高，………我们注意到气温y是随着时间x的变化而变化的：当x∈【4, 14】时，随着时间x的增大，气温y逐渐升高。
⑶ 你能用一个数学式子描述这种变化吗？如果请你表示这种变化，你会如何表示？比如：x=4, y=-2
x=7, y=0
就是时间从4点增大到7点时，气温从-2升高到0
⑷ 这种变化能否用一种数学式子表示？提示:⑸ 这是一个动态的变化过程，能否用4和7代表区间【4, 7】上的所有x吗？
你想到了什么办法?
联想:x∈【a, b】(其中a⑹ 随着时间x从4逐渐增大到14，气温y从-2上升到9，用数学式子如何表示“x增大”、 “ y升高？”
提示“上升”、“下降”、“增大”、“减小”等都含有比较大小的意思，当然至少两个量才可以比较。
⑺ 你能在区间【4, 14】上任意选择两个量并说明他们的大小关系？如何用数学式子表示？所有时间点x1，x2 ∈【4, 14】，
且 x1< x2时，都有y1 < y2。称气温y在
【4, 14】上是单调增函数。上述例子中，气温y是时间x的函数，将“气温y”变为”函数y”,“时间x”变为“自变量x”, “时间x的范围”变为 “自变量x的范围I”,上面的气温问题就变成了一般的函数问题。
⑻你能从函数y= f (x)的角度叙述函数的单调递增性吗？函数的单调性定义： 设函数y= f (x)的定义域为A，区间I A如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) < f(x2),
那么就说y= f (x) 在区间I上是增函数,
I称为y= f (x)单调增区间。函数的单调性定义： 设函数y= f (x)的定义域为A，区间I A如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) < f(x2),
那么就说y= f (x) 在区间I上是增函数,
I称为y= f (x)单调增区间。如果对于区间I内的任意两个值x1，x2 ，
当x1< x2时，都有f(x1) > f(x2),那么
就说y= f (x)在区间I上是减函数,
I称为y= f (x)单调减区间。0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx···· .根据图象说出函数的单调区间，以及在每一单调区间上，它是增函数还是减函数？
数学应用：
例1. 判断下列说法是否正确。2. 定义在R上的函数 f (x) 满足 f (-1) 函数的单调减区间为（0，2）；例2. 试判断函数y= x2 + 1 在（0，＋∞）上是增函数还是减函数？并给予证明。
解：函数y= x2 + 1 在（0，＋∞）上是增函数下面给予证明：设 x1，x2 为区间(0,＋∞)上的任意两个值，且x1 = (x1 – x2) (x1 + x2)
又 x2 ＞ x1 ＞ 0，所以x1 – x2< 0， x1 + x2 ＞0，
所以f (x1)– f (x2)<0所以函数y= x2 + 1 在（0，＋∞）上是增函数小结：在区间I内0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····判断函数单调性的方法：1、图象法 2、代数论证法证明函数的单调性常用步骤：(1)取值 (2)作差变形(3)定号 (4)结论思考题: 讨论函数y=x + (x ＞ 0)的单调性。1x作业：课本第40页
练习6、7