2.2.1 函数的单调性 课件 (3)
文档属性
| 名称 | 2.2.1 函数的单调性 课件 (3) |

|
|
| 格式 | zip | ||
| 文件大小 | 878.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-08 20:57:43 | ||
图片预览



文档简介
课件14张PPT。函数的单调性
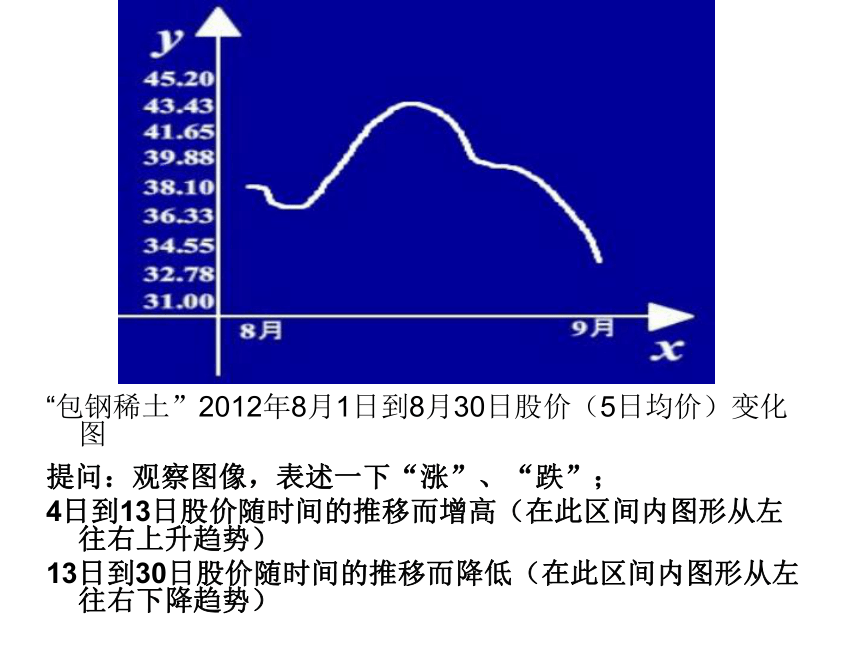
“包钢稀土”2012年8月1日到8月30日股价(5日均价)变化图
提问:观察图像,表述一下“涨”、“跌”;
4日到13日股价随时间的推移而增高(在此区间内图形从左往右上升趋势)
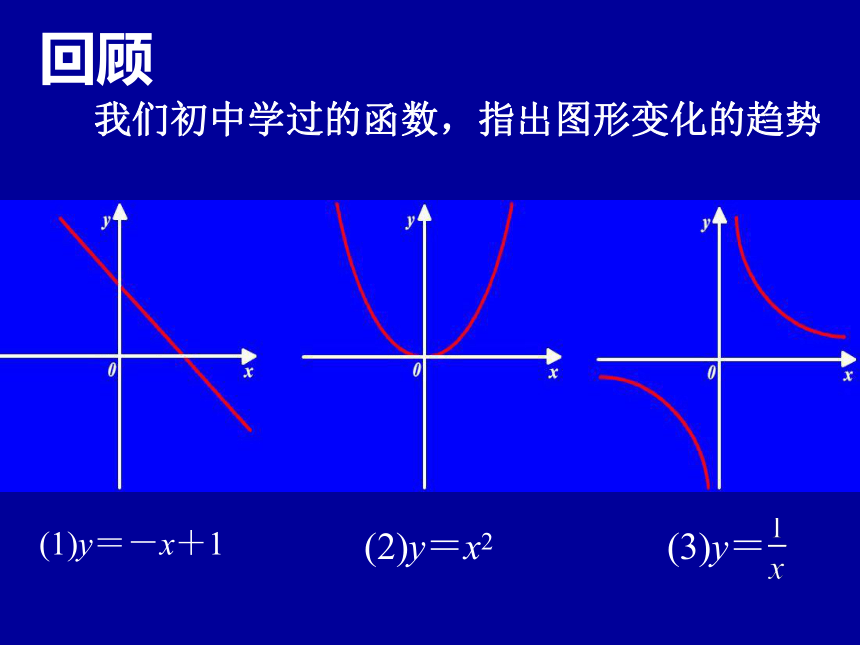
13日到30日股价随时间的推移而降低(在此区间内图形从左往右下降趋势)回顾我们初中学过的函数,指出图形变化的趋势 (1)y=-x+1(2)y=x2(3)y=提问:“形”的这种上升(下降)趋势在“数”上是如何体现的?
“从左向右看”
——x增大,
“从左向右上升趋势”
——随自变量x的增大,y也越来越大
“从左向右下降趋势”
—— 随自变量x的增大,y越来越小
如果函数在某个区间上随自变量x的增大,y也越来
越大,我们说函数在该区间上为增函数;如果函数
在某个区间上随自变量x的增大,y越来越小,我们说
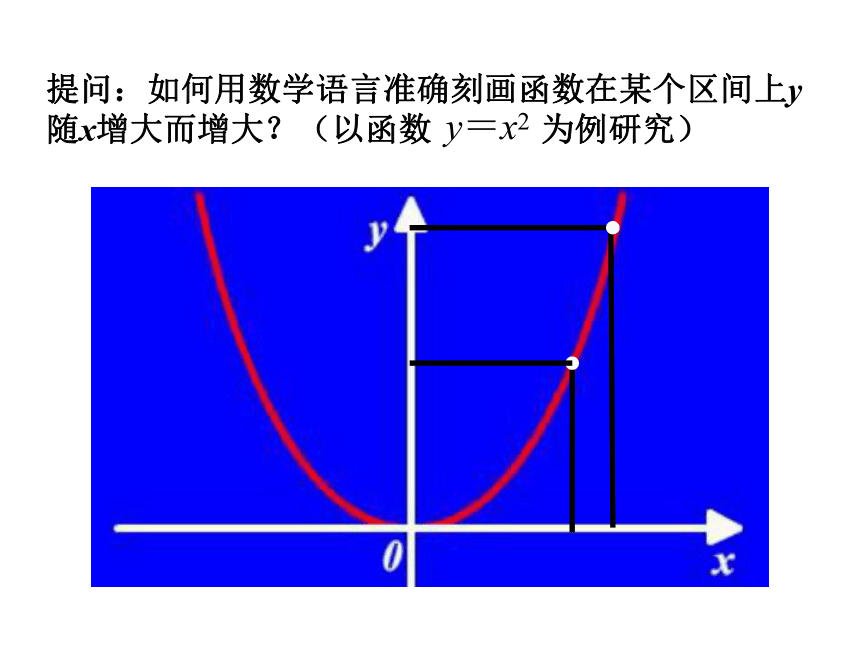
函数在该区间上为减函数.提问:如何用数学语言准确刻画函数在某个区间上y随x增大而增大?(以函数 为例研究)y=x2一般地,设函数y = f(x) 的定义域为A,区间I A. 如果对于区间I内的任意两个值x1、x2,当x1<x2时,都
有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数, I称为y=f(x)的单调增区间. 如果对于区间I内的任意两个值x1、x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间I上是单调减函数,I称为y=f(x)的单调减区间.
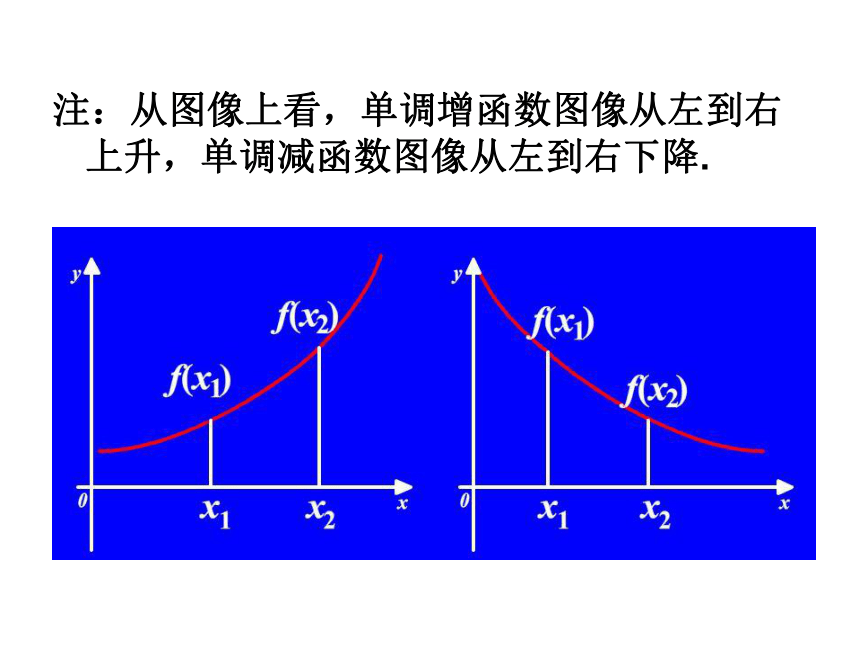
若函数y=f(x)在区间I上是单调增函数或单调减函数,那么就说函数y=f(x) 在区间I上具有单调性.单调增区间和单调减区间统称为单调区间. 1、单调增函数与单调减函数区间I任意当x1<x2时,都有f(x1)<f(x2)2、单调性、单调区间注:从图像上看,单调增函数图像从左到右上升,单调减函数图像从左到右下降.
O1.作出以下函数的图像,写出单调区间(1)y=-(x-2)2+4(2) y=- 2.试用单调性的定义证明:
函数 在 上是单调增函数.(-∞,0) y=-
3.证明:函数 在(2,+∞)上是单调减函数.y=-(x-2)2+4用定义法证明函数单调性的步骤:①取值;②作差变形;③定号;④判断.课堂小结
1.函数单调性的概念,单调增(减)函数的概念,注意关键词
2.判断函数单调性的方法: 图像(从“形”的角度)
3.证明函数的单调性的方法:定义(从“数”的角度)
4.数形结合的数学思想方法问题 讨论函数 的单调性.思考实际问题 在一碗水中,加入一定量的
糖,糖加得越多糖水就越甜.你能运用所
学过的数学知识来解说这一现象吗? 谢谢!
“包钢稀土”2012年8月1日到8月30日股价(5日均价)变化图
提问:观察图像,表述一下“涨”、“跌”;
4日到13日股价随时间的推移而增高(在此区间内图形从左往右上升趋势)
13日到30日股价随时间的推移而降低(在此区间内图形从左往右下降趋势)回顾我们初中学过的函数,指出图形变化的趋势 (1)y=-x+1(2)y=x2(3)y=提问:“形”的这种上升(下降)趋势在“数”上是如何体现的?
“从左向右看”
——x增大,
“从左向右上升趋势”
——随自变量x的增大,y也越来越大
“从左向右下降趋势”
—— 随自变量x的增大,y越来越小
如果函数在某个区间上随自变量x的增大,y也越来
越大,我们说函数在该区间上为增函数;如果函数
在某个区间上随自变量x的增大,y越来越小,我们说
函数在该区间上为减函数.提问:如何用数学语言准确刻画函数在某个区间上y随x增大而增大?(以函数 为例研究)y=x2一般地,设函数y = f(x) 的定义域为A,区间I A. 如果对于区间I内的任意两个值x1、x2,当x1<x2时,都
有f(x1)<f(x2),那么就说y=f(x)在区间I上是单调增函数, I称为y=f(x)的单调增区间. 如果对于区间I内的任意两个值x1、x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间I上是单调减函数,I称为y=f(x)的单调减区间.
若函数y=f(x)在区间I上是单调增函数或单调减函数,那么就说函数y=f(x) 在区间I上具有单调性.单调增区间和单调减区间统称为单调区间. 1、单调增函数与单调减函数区间I任意当x1<x2时,都有f(x1)<f(x2)2、单调性、单调区间注:从图像上看,单调增函数图像从左到右上升,单调减函数图像从左到右下降.
O1.作出以下函数的图像,写出单调区间(1)y=-(x-2)2+4(2) y=- 2.试用单调性的定义证明:
函数 在 上是单调增函数.(-∞,0) y=-
3.证明:函数 在(2,+∞)上是单调减函数.y=-(x-2)2+4用定义法证明函数单调性的步骤:①取值;②作差变形;③定号;④判断.课堂小结
1.函数单调性的概念,单调增(减)函数的概念,注意关键词
2.判断函数单调性的方法: 图像(从“形”的角度)
3.证明函数的单调性的方法:定义(从“数”的角度)
4.数形结合的数学思想方法问题 讨论函数 的单调性.思考实际问题 在一碗水中,加入一定量的
糖,糖加得越多糖水就越甜.你能运用所
学过的数学知识来解说这一现象吗? 谢谢!
