2.2.1 函数的单调性 课件 (4)
文档属性
| 名称 | 2.2.1 函数的单调性 课件 (4) |

|
|
| 格式 | zip | ||
| 文件大小 | 669.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-08 00:00:00 | ||
图片预览





文档简介
课件13张PPT。《函数的单调性》
教学目标:
(1) 使学生了解增、减函数的概念及单调
性,单调区间的概念
(2)使学生掌握判断一些简单函数单
调性的方法和步骤
教学重点:函数单调性的有关概念
教学难点:函数单调性的判断和证明
教学方式:讲练结合一、问题情境
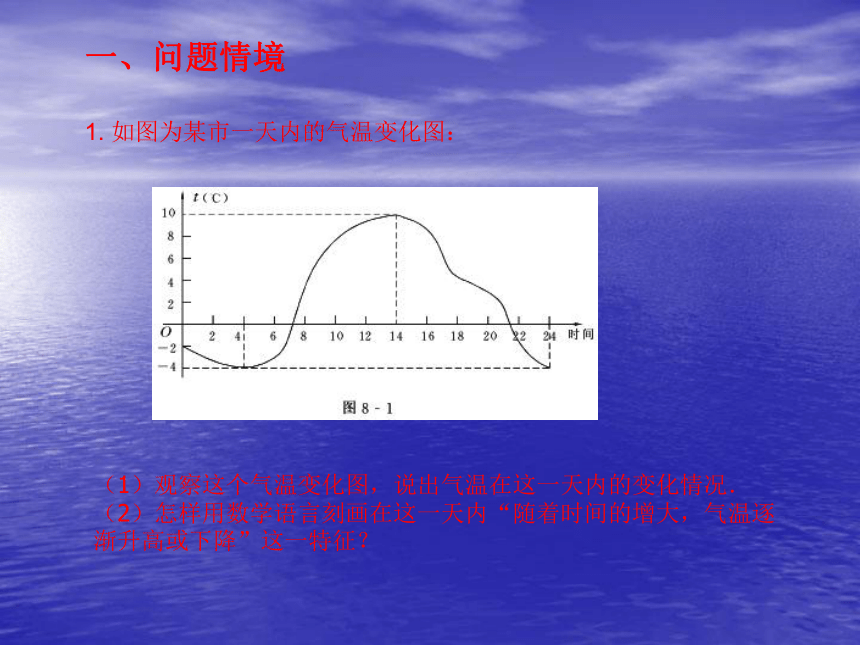
1. 如图为某市一天内的气温变化图:
(1)观察这个气温变化图,说出气温在这一天内的变化情况.
(2)怎样用数学语言刻画在这一天内“随着时间的增大,气温逐渐升高或下降”这一特征?
(1)y=2x. (2)y=-x+2. (3)y=x2
根据三个函数图像,分别指出当x∈(-∞,+∞)时,图像的变化趋势?2. 分别作出下列函数的图像: 以函数y=x2,x∈(-∞,0)为例,图像由左向右下降,意味着“随着x的增大,相应的函数值y=f(x)反而减小”,如何量化呢?取自变量的两个不同的值,如x1=-5,x2=-3,这时有x1<x2,f(x1)>f(x2),但是这种量化并不精确.因此,x1,x2应具有“任意性”.所以,在区间(-∞,0)上,任取两个x1,x2得到f(x1)=,f(x2)=.当x1<x2时,都有f(x1)>f(x2).这时,我们就说f(x)=x2在区间(-∞,0)上是减函数 设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么我们就说函数f(x)在区间D上是增函数[如图8-2(1)].
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么我们就说函数f(x)在区间D上是减函数[如图8-2(2)]. 如果函数y=f(x)在区间D上是增函数或减函数,那么我们就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫作y=f(x)的单调区间.
思考:
(1)定义在R上的函数f(x),满足f(2)>f(1),能否判断函数f(x)在R是增函数?
(2)定义在R上函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)上也是增函数,判断函数f(s)在R上是否为增函数.
(3)观察问题情境1中气温变化图像,根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数.[例 题]
1. 证明函数f(x)=2x+1,在(-∞,+∞)是增函数. 2. 证明函数f(x)=1/x,在区间(-∞,0)和(0,+∞)上都是减函数.证明:设x1,x2∈D,且x1<x2,
∵f(x)在区间D上保号,
∴f(x1)f(x2)>0.
又f(x)在区间D上为增函数,
∴f(x1)-f(x2)<0,
从而g(x1)-g(x2)>0,
∴g(x)在D上为减函数.[练 习]
1. 证明:(1)函数f(x)= 在(0,+∞)上是增函数.
(2)函数f(x)=x2-x在(-∞, ]上是减函数.
2. 判断函数的单调性,并写出相应的单调区间.
3. 如果函数y=f(x)是R上的增函数,判断g(x)=kf(x),(k≠0)在R上的单调性.拓展延伸
1. 根据图像,简要说明近150年来人类消耗能源的结构变化情况,并对未来100年能源结构的变化趋势作出预测.
2. 判断二次函数f(x)=ax2+bx+c,(a≠0)的单调性,并用定义加以证明.
3. 如果自变量的改变量Δx=x2-x1<0,函数值的改变量Δy=f(x2)-f(x1)>0,那么函数f(x)在区间D上是增函数还是减函数?课后作业: 1、 用定义证明函数f(x)=x3+2在R上是增函数。 2、已知定义在[1,4]上的函数f(x)是增函数,求满足不等式f(1-2a) -f(4+a)>0的a的取值范围。
教学目标:
(1) 使学生了解增、减函数的概念及单调
性,单调区间的概念
(2)使学生掌握判断一些简单函数单
调性的方法和步骤
教学重点:函数单调性的有关概念
教学难点:函数单调性的判断和证明
教学方式:讲练结合一、问题情境
1. 如图为某市一天内的气温变化图:
(1)观察这个气温变化图,说出气温在这一天内的变化情况.
(2)怎样用数学语言刻画在这一天内“随着时间的增大,气温逐渐升高或下降”这一特征?
(1)y=2x. (2)y=-x+2. (3)y=x2
根据三个函数图像,分别指出当x∈(-∞,+∞)时,图像的变化趋势?2. 分别作出下列函数的图像: 以函数y=x2,x∈(-∞,0)为例,图像由左向右下降,意味着“随着x的增大,相应的函数值y=f(x)反而减小”,如何量化呢?取自变量的两个不同的值,如x1=-5,x2=-3,这时有x1<x2,f(x1)>f(x2),但是这种量化并不精确.因此,x1,x2应具有“任意性”.所以,在区间(-∞,0)上,任取两个x1,x2得到f(x1)=,f(x2)=.当x1<x2时,都有f(x1)>f(x2).这时,我们就说f(x)=x2在区间(-∞,0)上是减函数 设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么我们就说函数f(x)在区间D上是增函数[如图8-2(1)].
如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么我们就说函数f(x)在区间D上是减函数[如图8-2(2)]. 如果函数y=f(x)在区间D上是增函数或减函数,那么我们就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫作y=f(x)的单调区间.
思考:
(1)定义在R上的函数f(x),满足f(2)>f(1),能否判断函数f(x)在R是增函数?
(2)定义在R上函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)上也是增函数,判断函数f(s)在R上是否为增函数.
(3)观察问题情境1中气温变化图像,根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数.[例 题]
1. 证明函数f(x)=2x+1,在(-∞,+∞)是增函数. 2. 证明函数f(x)=1/x,在区间(-∞,0)和(0,+∞)上都是减函数.证明:设x1,x2∈D,且x1<x2,
∵f(x)在区间D上保号,
∴f(x1)f(x2)>0.
又f(x)在区间D上为增函数,
∴f(x1)-f(x2)<0,
从而g(x1)-g(x2)>0,
∴g(x)在D上为减函数.[练 习]
1. 证明:(1)函数f(x)= 在(0,+∞)上是增函数.
(2)函数f(x)=x2-x在(-∞, ]上是减函数.
2. 判断函数的单调性,并写出相应的单调区间.
3. 如果函数y=f(x)是R上的增函数,判断g(x)=kf(x),(k≠0)在R上的单调性.拓展延伸
1. 根据图像,简要说明近150年来人类消耗能源的结构变化情况,并对未来100年能源结构的变化趋势作出预测.
2. 判断二次函数f(x)=ax2+bx+c,(a≠0)的单调性,并用定义加以证明.
3. 如果自变量的改变量Δx=x2-x1<0,函数值的改变量Δy=f(x2)-f(x1)>0,那么函数f(x)在区间D上是增函数还是减函数?课后作业: 1、 用定义证明函数f(x)=x3+2在R上是增函数。 2、已知定义在[1,4]上的函数f(x)是增函数,求满足不等式f(1-2a) -f(4+a)>0的a的取值范围。
