2.2.2 函数的奇偶性 课件 (1)
文档属性
| 名称 | 2.2.2 函数的奇偶性 课件 (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 418.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-08 00:00:00 | ||
图片预览








文档简介
课件21张PPT。函数的奇偶性 在我们的日常生活中,可以观察到许多对称现象:
美丽的蝴蝶
六角形的雪花晶体
建筑物和它在水中的倒影f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1) 实际上,对于函数f(x)=x2定义域 R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.观察这个函数的图象,
你能发现这个函数图象有什么特征吗?如果对于函数f(x)的定义域内的任意实数x,都有f(-x) = f(x) ,那么就把函数f(x)叫做偶函数。偶函数的定义f(-2)=1/2=-f(2)
f(-1)=1=-f(1)
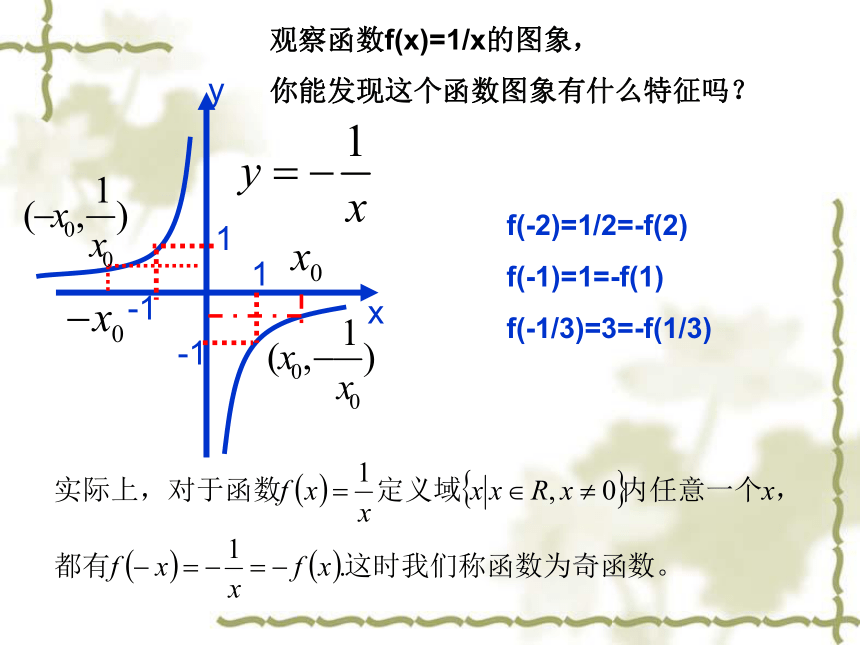
f(-1/3)=3=-f(1/3)观察函数f(x)=1/x的图象,
你能发现这个函数图象有什么特征吗?奇函数的定义如果对于函数f(x) 的定义域内的任意实数x, 都有f(-x) = - f(x) ,那么就把 函数f(x) 叫做奇函数。奇偶函数图像的特征特征偶函数的图像关于y轴对称(轴对称图形)奇函数的图像关于原点对称(中心对称图形)注意:
1、函数的奇偶性是函数的整体性质,是对整个函数而言的。
2、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性。
思考:1、具有奇偶性的函数,其定义域具有怎样的特点?
2、函数f(x)为奇函数,且在x=0处有意义,则f(0)=________
3、函数f(x)能否既是奇函数又是偶函数?既是奇函数又是偶函数的函数有多少个?
1、判断下列函数的奇偶性例题:判断函数奇偶性的一般步骤:①判断定义域是否为关于原点对称;②若函数的定义域关于原点对称,则判断f(-x)=f(x)(或f(-x)-f(x)=0)
f(-x)=-f(x)(或f(-x)+f(x)=0 )
是否成立, 从而判断函数的奇偶性。也可以结合函数的图像来判断函数的奇偶性注:函数奇偶性有四种可能:
1.奇函数;
2.偶函数;
3.既奇又偶;
4.非奇非偶。2、判定下列函数的奇偶性可以利用定义域关于原点对称解决问题练习:本课小结1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称谢谢指导!
美丽的蝴蝶
六角形的雪花晶体
建筑物和它在水中的倒影f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1) 实际上,对于函数f(x)=x2定义域 R内任意的一个x,都有f(-x)=(-x)2=x2=f(x),这时我们称函数y=x2为偶函数.观察这个函数的图象,
你能发现这个函数图象有什么特征吗?如果对于函数f(x)的定义域内的任意实数x,都有f(-x) = f(x) ,那么就把函数f(x)叫做偶函数。偶函数的定义f(-2)=1/2=-f(2)
f(-1)=1=-f(1)
f(-1/3)=3=-f(1/3)观察函数f(x)=1/x的图象,
你能发现这个函数图象有什么特征吗?奇函数的定义如果对于函数f(x) 的定义域内的任意实数x, 都有f(-x) = - f(x) ,那么就把 函数f(x) 叫做奇函数。奇偶函数图像的特征特征偶函数的图像关于y轴对称(轴对称图形)奇函数的图像关于原点对称(中心对称图形)注意:
1、函数的奇偶性是函数的整体性质,是对整个函数而言的。
2、如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性。
思考:1、具有奇偶性的函数,其定义域具有怎样的特点?
2、函数f(x)为奇函数,且在x=0处有意义,则f(0)=________
3、函数f(x)能否既是奇函数又是偶函数?既是奇函数又是偶函数的函数有多少个?
1、判断下列函数的奇偶性例题:判断函数奇偶性的一般步骤:①判断定义域是否为关于原点对称;②若函数的定义域关于原点对称,则判断f(-x)=f(x)(或f(-x)-f(x)=0)
f(-x)=-f(x)(或f(-x)+f(x)=0 )
是否成立, 从而判断函数的奇偶性。也可以结合函数的图像来判断函数的奇偶性注:函数奇偶性有四种可能:
1.奇函数;
2.偶函数;
3.既奇又偶;
4.非奇非偶。2、判定下列函数的奇偶性可以利用定义域关于原点对称解决问题练习:本课小结1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称谢谢指导!
