2.2.2 函数的奇偶性 课件 (3)
文档属性
| 名称 | 2.2.2 函数的奇偶性 课件 (3) |

|
|
| 格式 | zip | ||
| 文件大小 | 797.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-08 00:00:00 | ||
图片预览








文档简介
课件22张PPT。
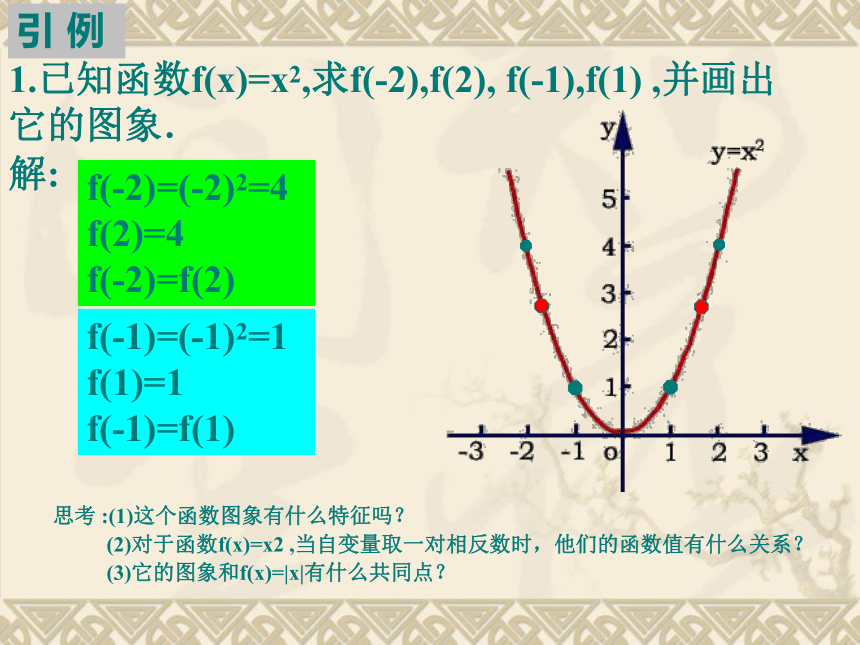
函数的基本性质——奇偶性引 例1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1) ,并画出它的图象.解:f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)思考 :(1)这个函数图象有什么特征吗?
(2)对于函数f(x)=x2?,当自变量取一对相反数时,他们的函数值有什么关系?
(3)它的图象和f(x)=|x|有什么共同点?偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.1. 偶函数的概念f(x)=x2?,x∈[-3,2]?是偶函数吗?偶函数的定义域有什么特征?思考:不是,偶函数的定义域关于原点对称?判断下列函数是否是偶函数?(口答)
?(1)f(x)=x2?,x∈[-1,1]
?(2)f(x)=x2?,x∈[-1,1)
?? (3)f(x)=x2??,x∈[-2,-1)∪??(1,2]
是不是是
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3 f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.1、判断下列函数是否是奇函数?
(1)f(x)=x3?,x∈?[-1,1]
??(2)f(x)=x3?,x∈?[-1,1)
?(3)f(x)=x3?,x∈?[-2,-1)∪?(1,2]思考:是是不是2、奇函数定义域是[a,2a+3],则a=_____-1 如果一个函数是奇函数,则这个函
数的图象以坐标原点为对称中心的中心
对称图形. 反之,如果一个函数的图象是
以坐标原点为对称中心的中心对称图形,
则这个函数是奇函数.
如果一个函数是偶函数,则它的图
形是以y轴为对称轴的轴对称图形;反之,
如果一个函数的图象关于y轴对称,则这
个函数是偶函数. 3. 奇函数与偶函数图象性质 奇函数、偶函数的图象性质1.奇函数的图象关于原点成中心对称图形;2.偶函数的图象关于y 轴成轴对称图形.奇偶函数图象的性质可用于:
①简化函数图象的画法;
②判断函数的奇偶性.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),例题分析解:函数定义域为R.∴f(x)为奇函数.有既奇又偶的函数来吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:奇函数;偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.4.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 例题2.
(1)、已知函数f(x)是定义域为R的奇函数,求f(0)的值;
(2)、已知函数f(x)=(m-2)x2?+(m-1)x+3是偶函数,求实数m的值; (3)、已知函数f(x)=x5+ax3+bx?8?若f(-2)=10,求f(2)的值。解: (1)f(0)=0
(2)m=1
(3)f(2)=-26变式训练:设函数f(x)是定义在R上的奇函数,当x0时f(x)=_________
解:令x>0,则-x<0
课堂小结1.函数奇偶性的定义. 定义法2.函数奇偶性的判定图象法:画出奇函数或者偶函数函数图象①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.当堂反馈:
1、判断函数的奇偶性:
2、若f(x)是定义在R上的奇函数,当x>0时,
函数的基本性质——奇偶性引 例1.已知函数f(x)=x2,求f(-2),f(2), f(-1),f(1) ,并画出它的图象.解:f(-2)=(-2)2=4 f(2)=4
f(-2)=f(2)f(-1)=(-1)2=1 f(1)=1
f(-1)=f(1)思考 :(1)这个函数图象有什么特征吗?
(2)对于函数f(x)=x2?,当自变量取一对相反数时,他们的函数值有什么关系?
(3)它的图象和f(x)=|x|有什么共同点?偶函数的特征:①解析式的基本特征:f (-x)=f (x)②图像特征:关于y轴对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫做偶函数.1. 偶函数的概念f(x)=x2?,x∈[-3,2]?是偶函数吗?偶函数的定义域有什么特征?思考:不是,偶函数的定义域关于原点对称?判断下列函数是否是偶函数?(口答)
?(1)f(x)=x2?,x∈[-1,1]
?(2)f(x)=x2?,x∈[-1,1)
?? (3)f(x)=x2??,x∈[-2,-1)∪??(1,2]
是不是是
2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),
f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8, f (2)=8
f(-2)= - f(2)f(-1)=(-1)3=-1, f(1)=1 f(-1)= - f(1)f(-x)=(-x)3=-x3 f(-x)=- f(x)思考 : 通过练习,你发现了什么规律?(-x,-y)(x,y)奇函数的特征:①解析式的基本特征:f (-x)=-f (x)②图像特征:关于原点对称. 如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.2.奇函数的概念 如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性.1、判断下列函数是否是奇函数?
(1)f(x)=x3?,x∈?[-1,1]
??(2)f(x)=x3?,x∈?[-1,1)
?(3)f(x)=x3?,x∈?[-2,-1)∪?(1,2]思考:是是不是2、奇函数定义域是[a,2a+3],则a=_____-1 如果一个函数是奇函数,则这个函
数的图象以坐标原点为对称中心的中心
对称图形. 反之,如果一个函数的图象是
以坐标原点为对称中心的中心对称图形,
则这个函数是奇函数.
如果一个函数是偶函数,则它的图
形是以y轴为对称轴的轴对称图形;反之,
如果一个函数的图象关于y轴对称,则这
个函数是偶函数. 3. 奇函数与偶函数图象性质 奇函数、偶函数的图象性质1.奇函数的图象关于原点成中心对称图形;2.偶函数的图象关于y 轴成轴对称图形.奇偶函数图象的性质可用于:
①简化函数图象的画法;
②判断函数的奇偶性.例1. 判断下列函数的奇偶性(1) f(x)=x3+2x; (2) f(x)=2x4+3x2;解:∵f(-x)=(-x)3+2(-x)= -x3-2x= -(x3+2x)= - f(x),∴f(x)为奇函数. ∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数.函数定义域为R.解:函数定义域为R.= f(x),例题分析解:函数定义域为R.∴f(x)为奇函数.有既奇又偶的函数来吗?解:函数定义域为 [0 ,+∞).
∵ 定义域不关于原点对称,
∴f(x)为非奇非偶函数.(6) f(x)=x+1解:函数f(x)的定义域为R.
∵ f(-x)=f(x)=0,
又 f(-x)=-f(x)=0,
∴f(x)为既奇又偶函数.(5)f(x)=0 (x?R)根据奇偶性, 函数可划分为四类:奇函数;偶函数;
既奇又偶函数;
非奇非偶函数.
解:函数定义域为R.
∵ f(-x)= -x+1, - f(x)= -x-1,
∴f(-x)≠f(x),且f(-x)≠ –f(x).
∴f(x)为非奇非偶函数.4.判定函数的奇偶性的步骤:
(1)先求函数的定义域;
①若定义域不是关于原点对称的区间,则函数为非奇非偶函数.
②若定义域是关于原点对称的区间,进入第二步;
(2)计算f(-x)化向 f ( x ) 的解析式;
①若等于 f ( x ),则函数是偶函数,
②若等于-f ( x ),则函数是奇函数,
③若不等于 ,则函数是非奇非偶函数
(3)结论.有时判定f(-x)=±f(x)比较困难,可考虑判定f(-x)±f(x)=0或判定f(x)/f(-x)=±1. 例题2.
(1)、已知函数f(x)是定义域为R的奇函数,求f(0)的值;
(2)、已知函数f(x)=(m-2)x2?+(m-1)x+3是偶函数,求实数m的值; (3)、已知函数f(x)=x5+ax3+bx?8?若f(-2)=10,求f(2)的值。解: (1)f(0)=0
(2)m=1
(3)f(2)=-26变式训练:设函数f(x)是定义在R上的奇函数,当x0时f(x)=_________
解:令x>0,则-x<0
课堂小结1.函数奇偶性的定义. 定义法2.函数奇偶性的判定图象法:画出奇函数或者偶函数函数图象①考查函数定义域是否关于原点对称;
②判断f(-x)=±f(x)之一是否成立;
③作出结论.当堂反馈:
1、判断函数的奇偶性:
2、若f(x)是定义在R上的奇函数,当x>0时,
