2.2.2 函数的奇偶性 课件 (4)
文档属性
| 名称 | 2.2.2 函数的奇偶性 课件 (4) |

|
|
| 格式 | zip | ||
| 文件大小 | 474.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-08 21:44:58 | ||
图片预览





文档简介
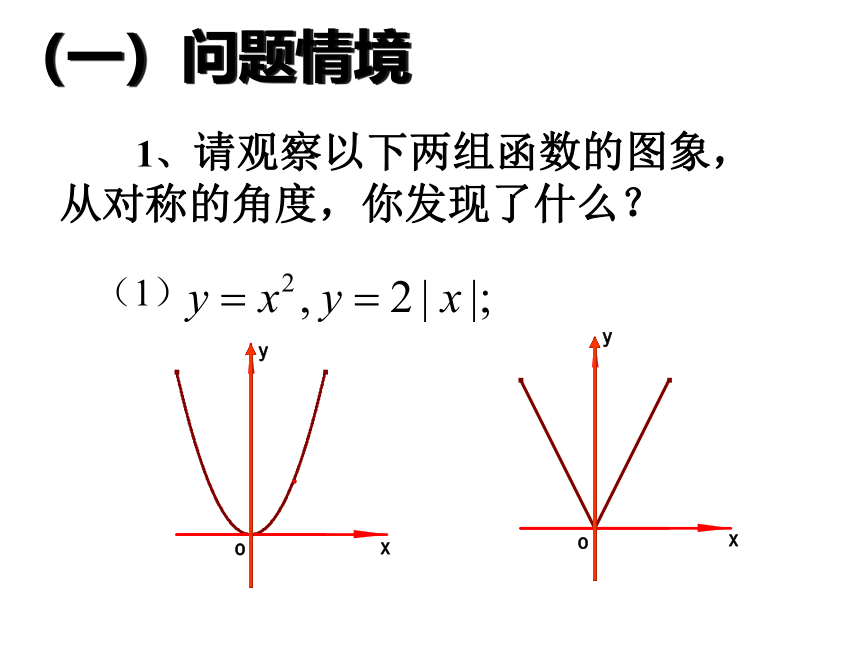
课件19张PPT。函数的奇偶性(一)问题情境 1、请观察以下两组函数的图象,从对称的角度,你发现了什么?(1)(2)
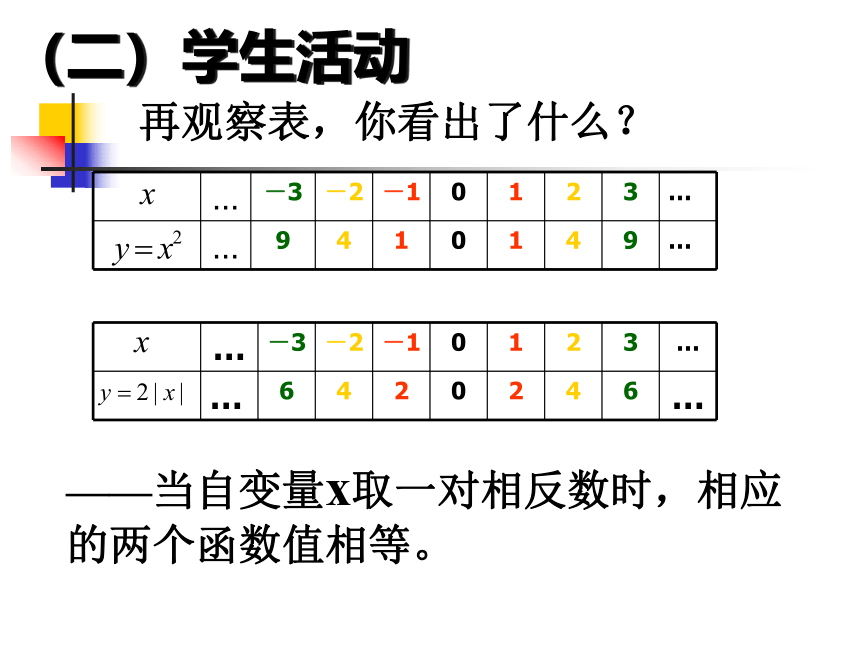
再观察表,你看出了什么?——当自变量x取一对相反数时,相应的两个函数值相等。(二)学生活动从以上的讨论,你能够得到什么? 一般地,如果对于函数 的定义域内的任意一个 ,都有 那么称函数 是偶函数;
请同学们考察:图象关于原点中心对称的函数与函数式有怎样的关系?(三)构建数学 一般地,如果对于函数 的定义域内的任意一个 ,都有 那么称该函数是奇函数;
——偶函数的图象关于y轴对称,奇函数的图象关于原点对称。【想一想】从对称的角度看,具有奇偶性函数的图象有什么特征?【探究】具有奇偶性的函数,满足
意味着其定义域满足怎样的条件?——定义域关于数“0”对称。
例1、判断下列函数是否为奇函数或偶函数:因为对任意的 都有所以函数 是偶函数。下结论(四)数学应用解:(1) 的定义域是 , 练习:
(1)函数 的大致图象可能是( ) (2)判断函数 的奇偶性;如图是函数 图象的一部分,请根据函数奇偶性画出它在y轴左侧的部分。例2、若函数 为奇函数,求 的值。思考:1.一次函数y=kx+b是奇函数吗?
2.反比例函数是奇函数吗?
3.二次函数一定是定义在R上的偶函数吗?
4.函数定义域对函数奇偶性有没有影响?
5. 有没有一个函数既是奇函数也是偶函数,请举出一例?
例3、判断函数 是否具有奇偶性? 数
(坐标)相等(五)回顾反思1、知识结论:函数的奇偶性及简单应用;2、思想与方法:形(图象对称)点(点对称)式相等( )。【作业】1:课本P40 1、2、3;
2:《教学与测试》P65-66
谢谢大家
再观察表,你看出了什么?——当自变量x取一对相反数时,相应的两个函数值相等。(二)学生活动从以上的讨论,你能够得到什么? 一般地,如果对于函数 的定义域内的任意一个 ,都有 那么称函数 是偶函数;
请同学们考察:图象关于原点中心对称的函数与函数式有怎样的关系?(三)构建数学 一般地,如果对于函数 的定义域内的任意一个 ,都有 那么称该函数是奇函数;
——偶函数的图象关于y轴对称,奇函数的图象关于原点对称。【想一想】从对称的角度看,具有奇偶性函数的图象有什么特征?【探究】具有奇偶性的函数,满足
意味着其定义域满足怎样的条件?——定义域关于数“0”对称。
例1、判断下列函数是否为奇函数或偶函数:因为对任意的 都有所以函数 是偶函数。下结论(四)数学应用解:(1) 的定义域是 , 练习:
(1)函数 的大致图象可能是( ) (2)判断函数 的奇偶性;如图是函数 图象的一部分,请根据函数奇偶性画出它在y轴左侧的部分。例2、若函数 为奇函数,求 的值。思考:1.一次函数y=kx+b是奇函数吗?
2.反比例函数是奇函数吗?
3.二次函数一定是定义在R上的偶函数吗?
4.函数定义域对函数奇偶性有没有影响?
5. 有没有一个函数既是奇函数也是偶函数,请举出一例?
例3、判断函数 是否具有奇偶性? 数
(坐标)相等(五)回顾反思1、知识结论:函数的奇偶性及简单应用;2、思想与方法:形(图象对称)点(点对称)式相等( )。【作业】1:课本P40 1、2、3;
2:《教学与测试》P65-66
谢谢大家
