3.1.2 指数函数 课件 (3)

课件15张PPT。指数函数及其性质分裂
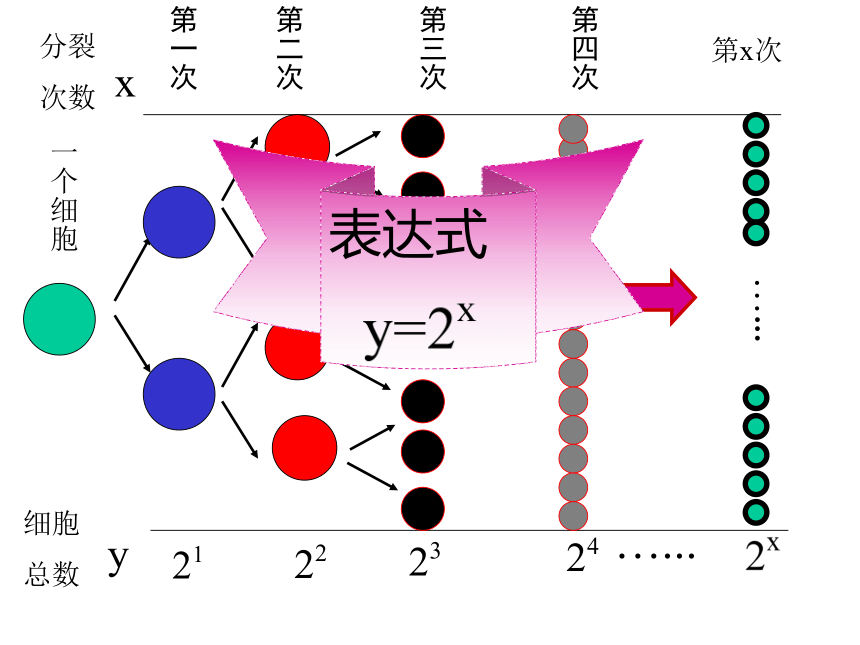
次数第一次第二次第三次第四次第x次…...x设问1：像y=2x这样的函数与我们学过的y=x，y=x2，y=x-1这样的函数一样吗？有什么区别?
答：不一样。前一个函数的自变量在指数位置上，而底数为常数；后三个函数的自变量在底数位置上，指数为常数。指数函数的定义:
一般地，函数 叫做指数函数，其中 x 是自变量, 函数的定义域是 R。判断一个函数是否为指数函数的依据:
是否是形如 的函数,其中系数为1,底数满足 ,指数位置上是自变量x。为什么要规定a>0,且a1呢？ ①若a=0，则当x>0时，=0；0时，无意义. 当x ②若a<0，则对于x的某些数值，可使无意义. 如 ③若a=1，则对于任何xR，=1，是一个常量，没有研究的必要性. 为了便于研究，规定：a>0 ,且a≠1在规定以后，对于任何xR，都有意义，且>0. 因此指数函数的定义域是R，值域是(0,+∞). 时就没有意义 。想一想：识记与理解 ? 练习：
（口答）判断下列函数是不是指 数函数，为什么？√√例1 已知指数函数
的图象经过点(2, 4)，求f(0), f(1), f(-3)。 解: 因为 的图象经过点(2, 4),所以
f(2)=4,
即 ,
解得 a=2 ,于是
f(x)=
所以, f(0)=1, f(1)=2, f(-3)=1/8 .设问2：得到函数的图象一般用什
么方法？列表、描点、连线作图在同一坐标系中分别作出如下函数的图像:列表如下：在同一坐标系中分别作出如下函数的图像：练习：列表如下：( )( )() 通过作图，我们发现y=ax的图象大致分两种类型，即0＜a＜1和a＞1，图象如下：小结:1.本节课学了哪些知识?指数函数的定义
指数函数的图象2.记住两个基本图形:思考题?1.下列以x为自变量的函数中,是指数函数的是( ) 2. 函数 是指数函数,则a=_____