22.2 相似三角形的判定 同步练习(含答案)
文档属性
| 名称 | 22.2 相似三角形的判定 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
22.2 相似三角形的判定
一、单选题
1.(2024八下·东营月考)如图所示,给出下列条件:①;②;③;④.其中能够单独判定的个数为( )
A.1 B.2 C.3 D.4
2.(2025九上·济南期末)如图,点在的边上,添加一个条件,使得,下列不正确的是( )
A. B. C. D.
3.如图,矩形ABCD中,AE=BF,EF与BD相交于点G,则图中相似三角形共有( )
A.2对 B.4对 C.6对 D.8对
4.(2025九下·宁南月考)如图,四边形的对角线平分,补充下列条件后仍不能判定和相似的是( )
A. B. C. D.
5.(2024九上·金乡县期末)如图所示,若,则需满足( )
A. B. C. D.
6.(2024九下·南京模拟)如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有【 】
A.1对 B.2对 C.3对 D.4对
7.(2017·奉贤模拟)在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判断△ABC和△DEF相似的是( )
A. = B. = C.∠A=∠E D.∠B=∠D
8.(2022九下·北京市开学考)如图,下列选项中不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB
C.AC2=AD AB D.BC2=BD AB
9.(2017·西固模拟)如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A. B. C.或 D.或
10.(2023·惠阳模拟)如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF,有以下结论:
①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,;④BE+DF=EF.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2024九上·安吉月考)如图,,请补充—个条件: ,使(只写一个答案即可).
12.(2022九上·昌黎期中)如图所示,添加一个条件 ,△ADB ∽△ABC.
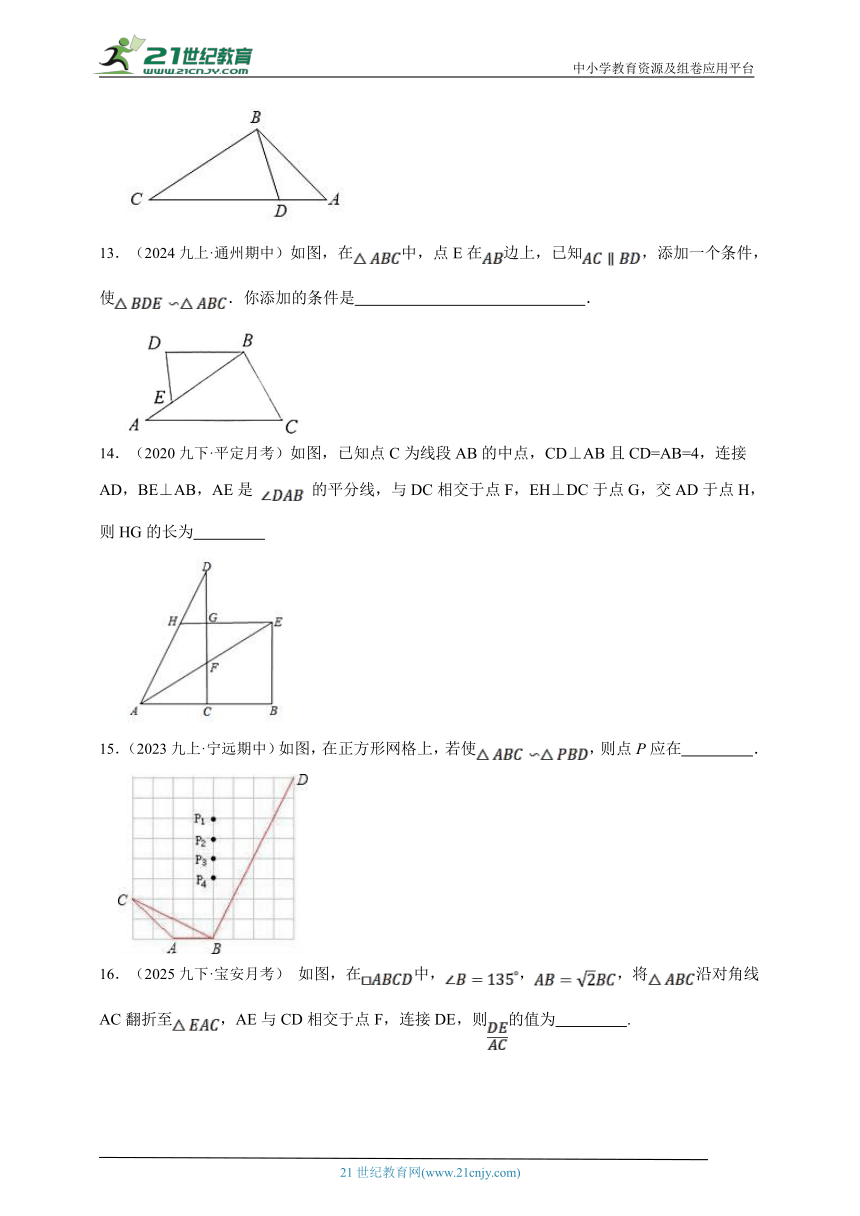
13.(2024九上·通州期中)如图,在中,点E在边上,已知,添加一个条件,使.你添加的条件是 .
14.(2020九下·平定月考)如图,已知点C为线段AB的中点,CD⊥AB且CD=AB=4,连接AD,BE⊥AB,AE是 的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为
15.(2023九上·宁远期中)如图,在正方形网格上,若使,则点P应在 .
16.(2025九下·宝安月考) 如图,在中,,,将沿对角线AC翻折至,AE与CD相交于点F,连接DE,则的值为 .
三、计算题
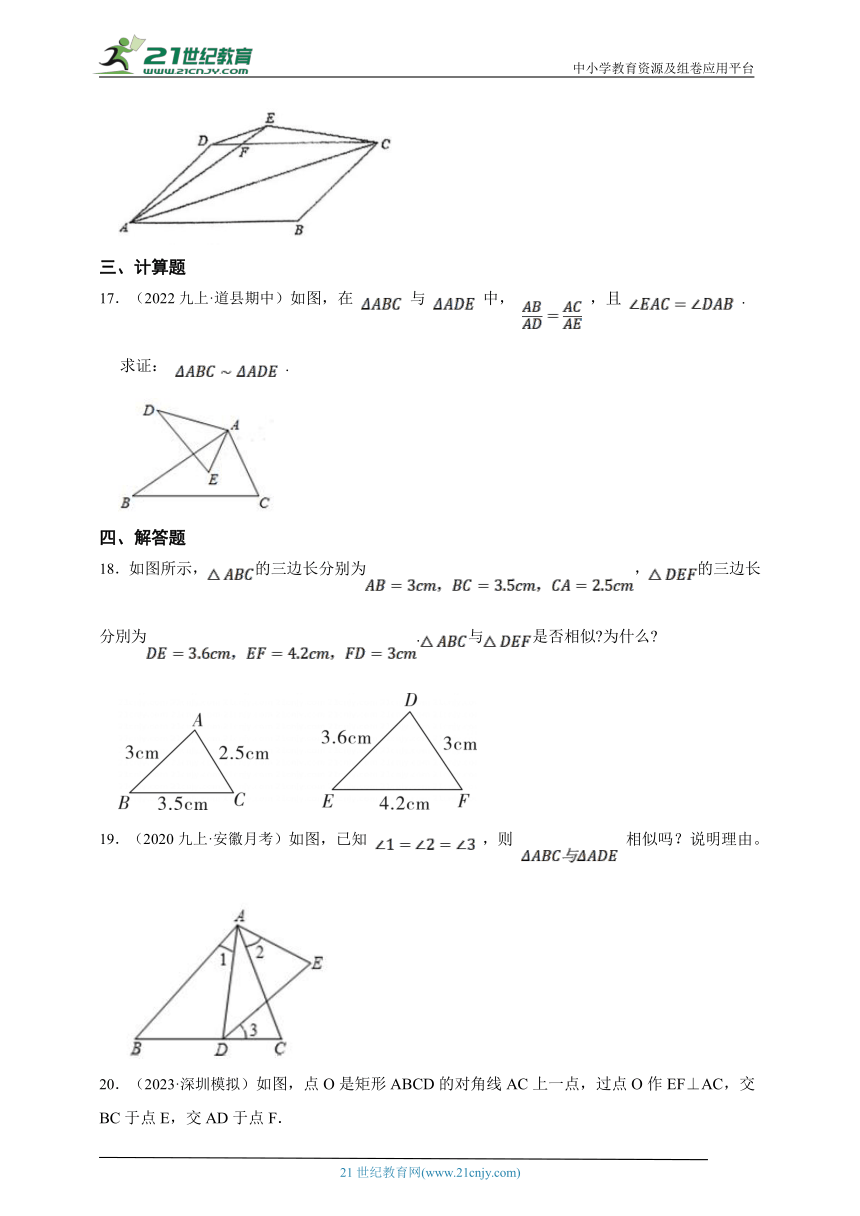
17.(2022九上·道县期中)如图,在 与 中, ,且 .
求证: .
四、解答题
18.如图所示,的三边长分别为,的三边长分別为.与是否相似 为什么
19.(2020九上·安徽月考)如图,已知 ,则 相似吗?说明理由。
20.(2023·深圳模拟)如图,点O是矩形ABCD的对角线AC上一点,过点O作EF⊥AC,交BC于点E,交AD于点F.
(1)在不添加新的点和线的前提下,请增加一个条件: ▲ ,使得OE=OF,并说明理由;
(2)若OE=OF,AB=6,BC=8,求EF的长.
21.(2017八下·黑龙江期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定
3.【答案】C
【知识点】矩形的性质;相似三角形的判定
4.【答案】D
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】C
【知识点】相似三角形的判定
7.【答案】B
【知识点】等腰三角形的性质;相似三角形的判定
8.【答案】D
【知识点】相似三角形的判定
9.【答案】C
【知识点】相似三角形的判定
10.【答案】D
【知识点】正方形的判定与性质;相似三角形的判定
11.【答案】∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD AC=AB AE(填一个即可).
【知识点】相似三角形的判定
12.【答案】∠ABD=∠ACB (∠ADB=∠ABC或)
【知识点】相似三角形的判定
13.【答案】(答案不唯一)
【知识点】相似三角形的判定
14.【答案】3-
【知识点】角平分线的性质;相似三角形的判定
15.【答案】
【知识点】相似三角形的判定
16.【答案】
【知识点】翻折变换(折叠问题);相似三角形的判定;三角形全等的判定-AAS
17.【答案】证明:∵ ,
∴ ,
即 ,
又 ,
∴ .
【知识点】相似三角形的判定
18.【答案】解:.,理由如下:
∴.
【知识点】相似三角形的判定
19.【答案】解:相似.理由如下:
∵ , ,且∠1=∠3,
∴ ,
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
【知识点】相似三角形的判定
20.【答案】(1)解:AO=CO;
理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAO=∠ECO,
∵EF⊥AC,
∴∠AOF=∠COE=90°,
又∵AO=CO,
∴△AOF≌△COE(ASA),
∴OF=OE.
(2)解:∵∵四边形ABCD是矩形,
∴∠B=90°,AD//BC,
又∵AB=6,BC=8,
∴AC==10,
∵AD∥BC,
∴∠FAO=∠ECO,∠AFO=∠CEO,
又∵EO=FO,
∴△AOF≌△COE(AAS),
∴AO=CO=5,
∵EF⊥AC,
∴∠COE=∠B=90°,
又∵∠OCE=∠BCA,
∴△OCE∽△BCA.
∴,
即
∴,
∴EF=.
【知识点】三角形全等的判定;矩形的性质;相似三角形的判定
21.【答案】(1)解:∵∠ACB=90°,AC=3,BC=4,
∴AB= =5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)解:∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t< )时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴ 或 ,
∴t= 或t= ;
当AD>AE(即t> )时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴ 或 ,
解得t= 或t= ;
综上所述,当t= 或 或 或 时,△DEG与△ACB相似
【知识点】勾股定理;相似三角形的判定;线段的中点
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
22.2 相似三角形的判定
一、单选题
1.(2024八下·东营月考)如图所示,给出下列条件:①;②;③;④.其中能够单独判定的个数为( )
A.1 B.2 C.3 D.4
2.(2025九上·济南期末)如图,点在的边上,添加一个条件,使得,下列不正确的是( )
A. B. C. D.
3.如图,矩形ABCD中,AE=BF,EF与BD相交于点G,则图中相似三角形共有( )
A.2对 B.4对 C.6对 D.8对
4.(2025九下·宁南月考)如图,四边形的对角线平分,补充下列条件后仍不能判定和相似的是( )
A. B. C. D.
5.(2024九上·金乡县期末)如图所示,若,则需满足( )
A. B. C. D.
6.(2024九下·南京模拟)如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=BC.图中相似三角形共有【 】
A.1对 B.2对 C.3对 D.4对
7.(2017·奉贤模拟)在△ABC和△DEF中,AB=AC,DE=DF,根据下列条件,能判断△ABC和△DEF相似的是( )
A. = B. = C.∠A=∠E D.∠B=∠D
8.(2022九下·北京市开学考)如图,下列选项中不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB
C.AC2=AD AB D.BC2=BD AB
9.(2017·西固模拟)如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
A. B. C.或 D.或
10.(2023·惠阳模拟)如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF,有以下结论:
①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,;④BE+DF=EF.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2024九上·安吉月考)如图,,请补充—个条件: ,使(只写一个答案即可).
12.(2022九上·昌黎期中)如图所示,添加一个条件 ,△ADB ∽△ABC.
13.(2024九上·通州期中)如图,在中,点E在边上,已知,添加一个条件,使.你添加的条件是 .
14.(2020九下·平定月考)如图,已知点C为线段AB的中点,CD⊥AB且CD=AB=4,连接AD,BE⊥AB,AE是 的平分线,与DC相交于点F,EH⊥DC于点G,交AD于点H,则HG的长为
15.(2023九上·宁远期中)如图,在正方形网格上,若使,则点P应在 .
16.(2025九下·宝安月考) 如图,在中,,,将沿对角线AC翻折至,AE与CD相交于点F,连接DE,则的值为 .
三、计算题
17.(2022九上·道县期中)如图,在 与 中, ,且 .
求证: .
四、解答题
18.如图所示,的三边长分别为,的三边长分別为.与是否相似 为什么
19.(2020九上·安徽月考)如图,已知 ,则 相似吗?说明理由。
20.(2023·深圳模拟)如图,点O是矩形ABCD的对角线AC上一点,过点O作EF⊥AC,交BC于点E,交AD于点F.
(1)在不添加新的点和线的前提下,请增加一个条件: ▲ ,使得OE=OF,并说明理由;
(2)若OE=OF,AB=6,BC=8,求EF的长.
21.(2017八下·黑龙江期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
答案解析部分
1.【答案】C
【知识点】相似三角形的判定
2.【答案】C
【知识点】相似三角形的判定
3.【答案】C
【知识点】矩形的性质;相似三角形的判定
4.【答案】D
【知识点】相似三角形的判定
5.【答案】D
【知识点】相似三角形的判定
6.【答案】C
【知识点】相似三角形的判定
7.【答案】B
【知识点】等腰三角形的性质;相似三角形的判定
8.【答案】D
【知识点】相似三角形的判定
9.【答案】C
【知识点】相似三角形的判定
10.【答案】D
【知识点】正方形的判定与性质;相似三角形的判定
11.【答案】∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD AC=AB AE(填一个即可).
【知识点】相似三角形的判定
12.【答案】∠ABD=∠ACB (∠ADB=∠ABC或)
【知识点】相似三角形的判定
13.【答案】(答案不唯一)
【知识点】相似三角形的判定
14.【答案】3-
【知识点】角平分线的性质;相似三角形的判定
15.【答案】
【知识点】相似三角形的判定
16.【答案】
【知识点】翻折变换(折叠问题);相似三角形的判定;三角形全等的判定-AAS
17.【答案】证明:∵ ,
∴ ,
即 ,
又 ,
∴ .
【知识点】相似三角形的判定
18.【答案】解:.,理由如下:
∴.
【知识点】相似三角形的判定
19.【答案】解:相似.理由如下:
∵ , ,且∠1=∠3,
∴ ,
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
∴∠BAC=∠DAE,
∴△ABC∽△ADE.
【知识点】相似三角形的判定
20.【答案】(1)解:AO=CO;
理由如下:
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FAO=∠ECO,
∵EF⊥AC,
∴∠AOF=∠COE=90°,
又∵AO=CO,
∴△AOF≌△COE(ASA),
∴OF=OE.
(2)解:∵∵四边形ABCD是矩形,
∴∠B=90°,AD//BC,
又∵AB=6,BC=8,
∴AC==10,
∵AD∥BC,
∴∠FAO=∠ECO,∠AFO=∠CEO,
又∵EO=FO,
∴△AOF≌△COE(AAS),
∴AO=CO=5,
∵EF⊥AC,
∴∠COE=∠B=90°,
又∵∠OCE=∠BCA,
∴△OCE∽△BCA.
∴,
即
∴,
∴EF=.
【知识点】三角形全等的判定;矩形的性质;相似三角形的判定
21.【答案】(1)解:∵∠ACB=90°,AC=3,BC=4,
∴AB= =5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)解:∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t< )时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴ 或 ,
∴t= 或t= ;
当AD>AE(即t> )时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴ 或 ,
解得t= 或t= ;
综上所述,当t= 或 或 或 时,△DEG与△ACB相似
【知识点】勾股定理;相似三角形的判定;线段的中点
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
