小升初暑假专项提升测试卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版
文档属性
| 名称 | 小升初暑假专项提升测试卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 21:38:12 | ||
图片预览

文档简介
小升初暑假专项提升测试卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版
学校:___________姓名:___________班级:___________考号:___________
一、作图题
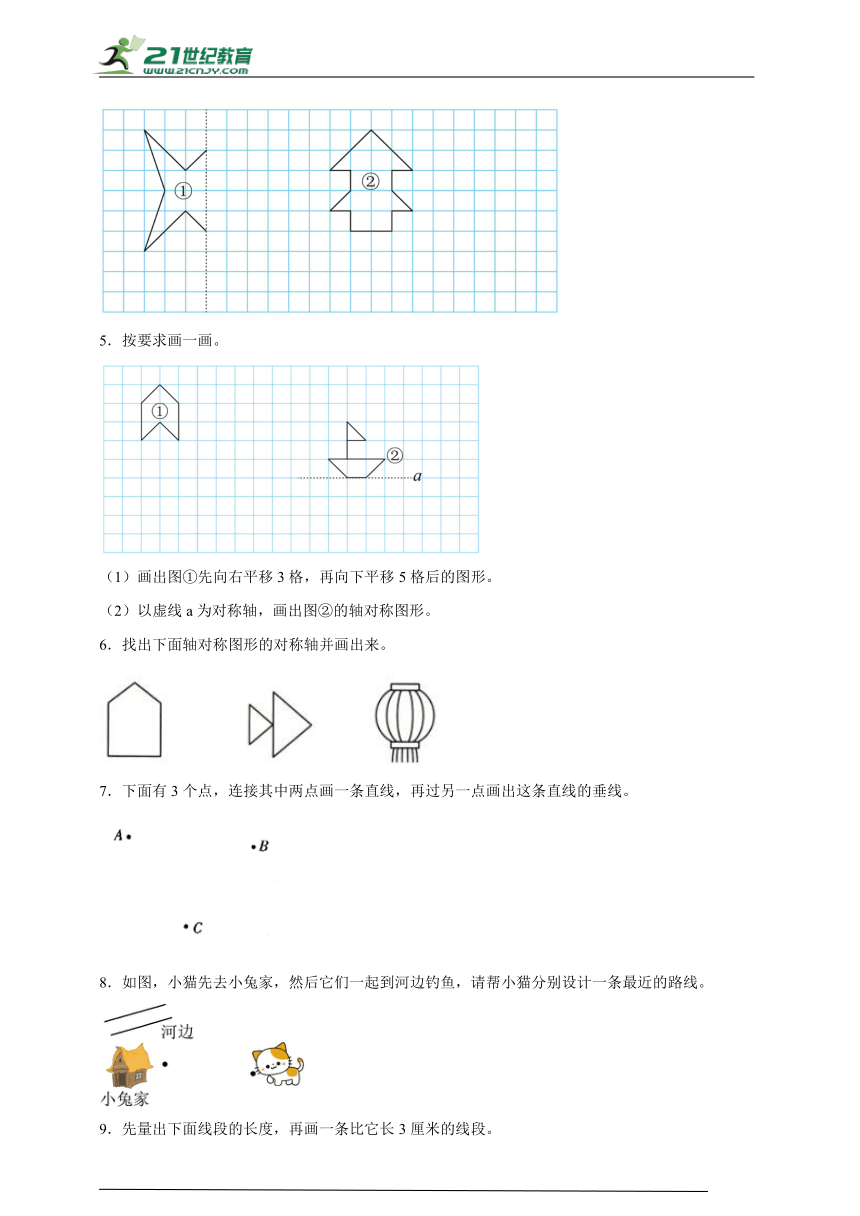
1.王强在篮球场打球。现在处,他要先去点捡球再尽快离开球场。请帮他设计一条最快离开球场的线路,在图中画出来。
2.在点子图中按要求画图。
3.按分数圈一圈。
4.(1)画出以虚线为对称轴,图形①的另一半图形。
(2)画出图②向右平移6格,再向下平移3格的图形。
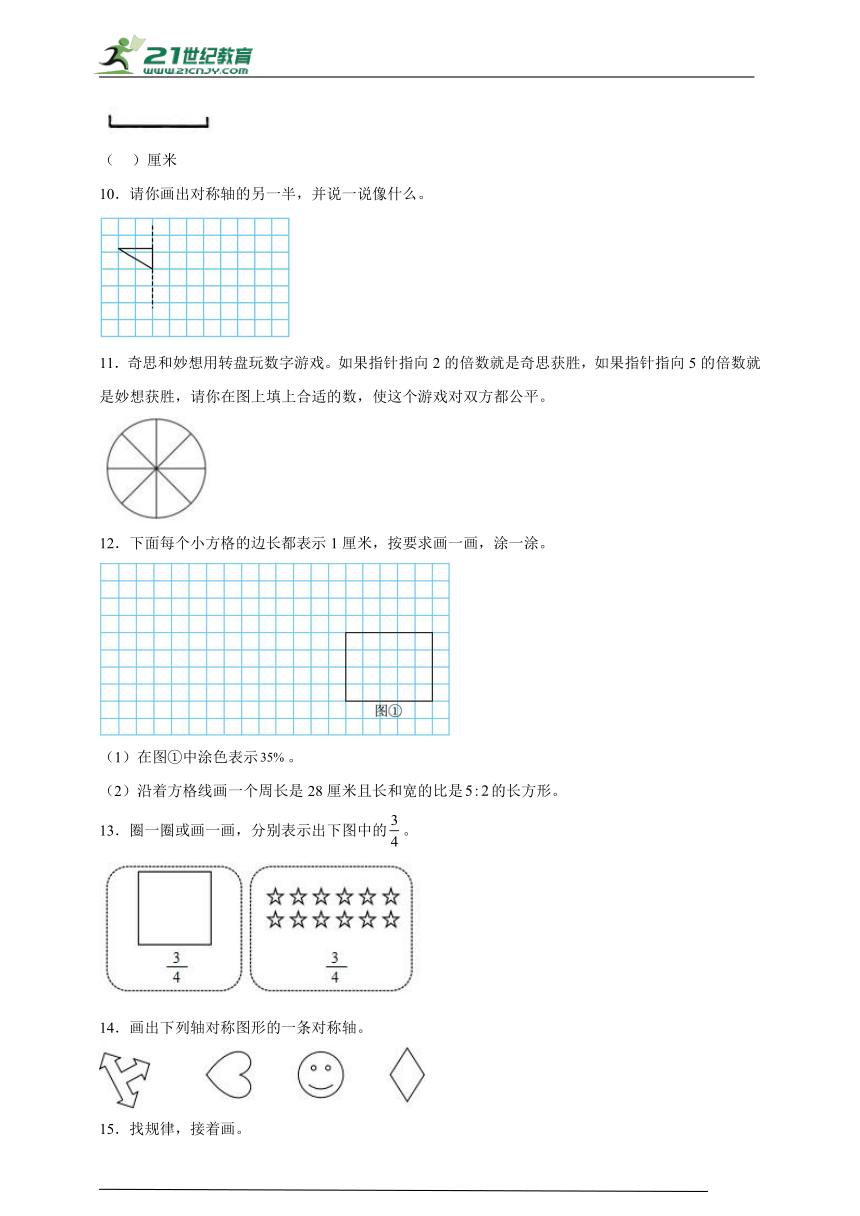
5.按要求画一画。
(1)画出图①先向右平移3格,再向下平移5格后的图形。
(2)以虚线a为对称轴,画出图②的轴对称图形。
6.找出下面轴对称图形的对称轴并画出来。
7.下面有3个点,连接其中两点画一条直线,再过另一点画出这条直线的垂线。
8.如图,小猫先去小兔家,然后它们一起到河边钓鱼,请帮小猫分别设计一条最近的路线。
9.先量出下面线段的长度,再画一条比它长3厘米的线段。
( )厘米
10.请你画出对称轴的另一半,并说一说像什么。
11.奇思和妙想用转盘玩数字游戏。如果指针指向2的倍数就是奇思获胜,如果指针指向5的倍数就是妙想获胜,请你在图上填上合适的数,使这个游戏对双方都公平。
12.下面每个小方格的边长都表示1厘米,按要求画一画,涂一涂。
(1)在图①中涂色表示。
(2)沿着方格线画一个周长是28厘米且长和宽的比是的长方形。
13.圈一圈或画一画,分别表示出下图中的。
14.画出下列轴对称图形的一条对称轴。
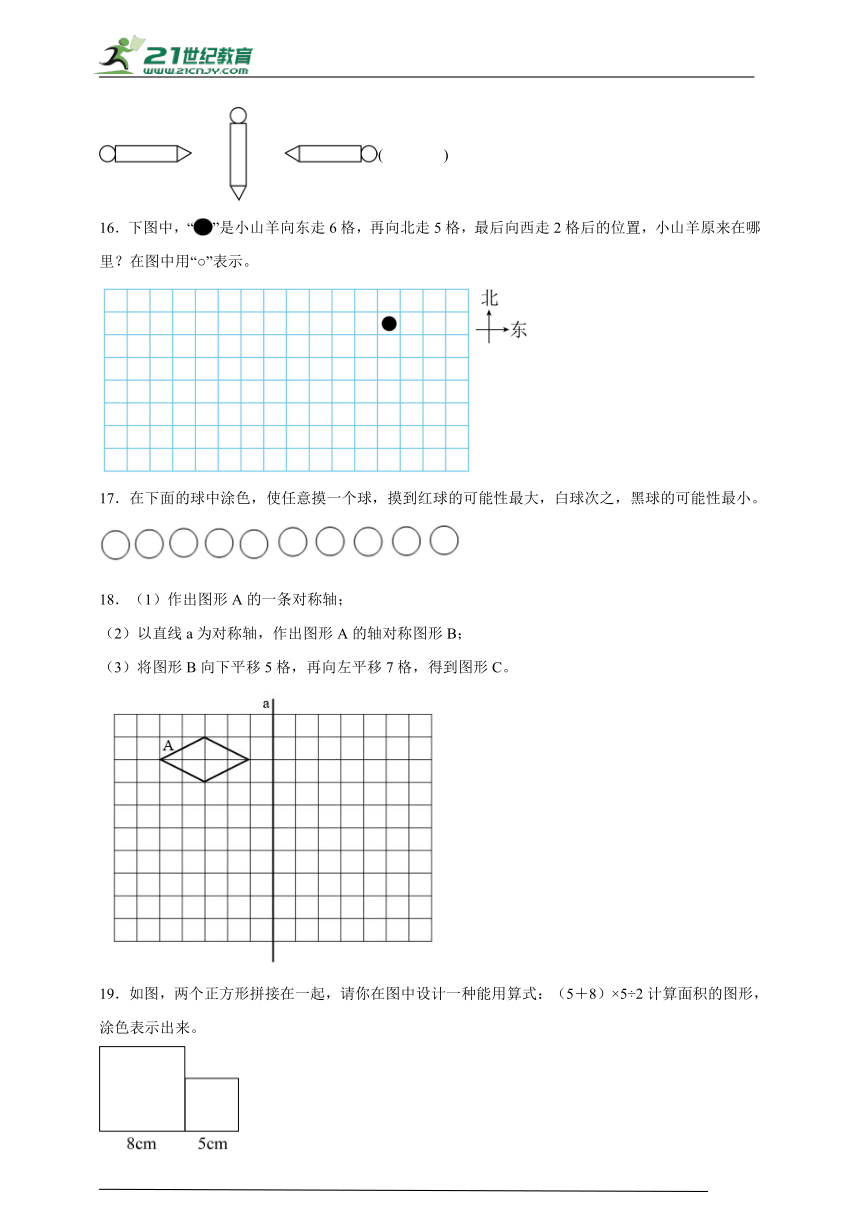
15.找规律,接着画。
( )
16.下图中,“”是小山羊向东走6格,再向北走5格,最后向西走2格后的位置,小山羊原来在哪里?在图中用“○”表示。
17.在下面的球中涂色,使任意摸一个球,摸到红球的可能性最大,白球次之,黑球的可能性最小。
18.(1)作出图形A的一条对称轴;
(2)以直线a为对称轴,作出图形A的轴对称图形B;
(3)将图形B向下平移5格,再向左平移7格,得到图形C。
19.如图,两个正方形拼接在一起,请你在图中设计一种能用算式:(5+8)×5÷2计算面积的图形,涂色表示出来。
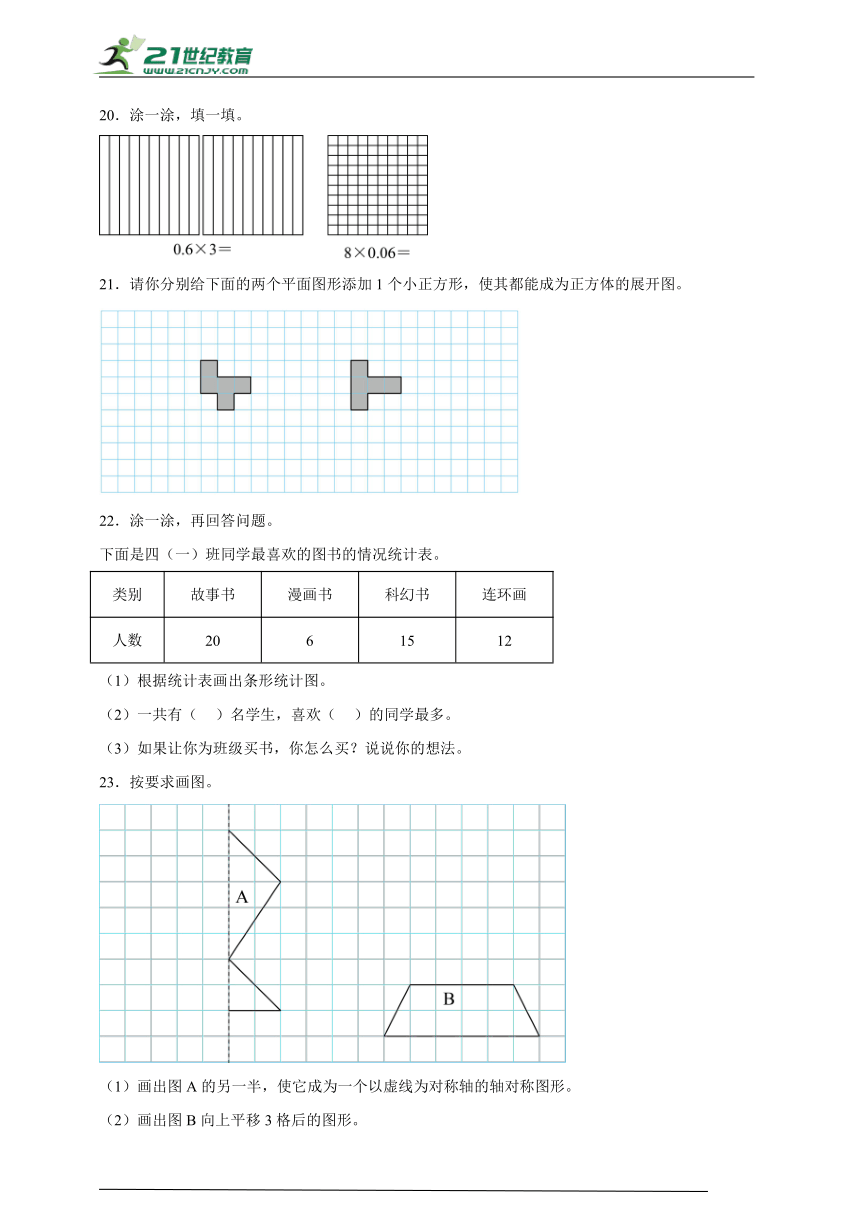
20.涂一涂,填一填。
21.请你分别给下面的两个平面图形添加1个小正方形,使其都能成为正方体的展开图。
22.涂一涂,再回答问题。
下面是四(一)班同学最喜欢的图书的情况统计表。
类别 故事书 漫画书 科幻书 连环画
人数 20 6 15 12
(1)根据统计表画出条形统计图。
(2)一共有( )名学生,喜欢( )的同学最多。
(3)如果让你为班级买书,你怎么买?说说你的想法。
23.按要求画图。
(1)画出图A的另一半,使它成为一个以虚线为对称轴的轴对称图形。
(2)画出图B向上平移3格后的图形。
24.为振兴乡村,方便A村的人民出行,计划修一条通往公路的柏油路。怎样修路最近?请画出来。
25.在下面的方格纸上画一个等腰直角三角形,一个梯形和一个平行四边形。
26.想一想,分别画出下面立体图形从正面、上面和左面看到的形状。
27.下图中每个小方格的边长是1厘米。
(1)点A用数对表示是( , ),点C用数对表示是( , )。
(2)计算某梯形面积的算式是(2+4)×4÷2,根据这个算式在方格图中把以A、B、C为3个顶点的梯形画完整。
(3)一只蚂蚁每秒爬行0.5厘米,它从C点向正东方向爬行了6秒,到达点E,请以E点为一个顶点,画一个与上面的梯形面积相等的三角形。
28.奇思一开始站在小树的位置,他向东走用正数表示,向西走用负数表示。他先走了﹢3米,再走了﹣7米,最后又走了﹢5米。请你用▲分别标出他三次行走后到达的位置。(每段表示1米)
29.画出方格中图形的轴对称图形,再将画完整的图形向左平移3格。
30.根据分数涂色。
31.先按左边的分数圈一圈,再在圈出的图形上涂上你喜欢的颜色。
32.估一估,分别在下图中标出a、b、c的大概位置。
5.4÷5=a 4.01÷0.98=b 5÷1.05=c
33.在钟面上画出时针和分针表示整时,并让它们所成的角等于给定的度数。
34.在方格纸上画出等腰三角形、梯形和平行四边形各一个。
35.欢欢和妹妹在院子里玩“看不看得见”的游戏,欢欢站在墙的一侧不动,妹妹在墙的另一侧活动,为了不让欢欢看见妹妹,请你画出妹妹可以活动的区域。
36.操作题。
移一移,描一描。
把图形①向右平移4格,把图形②向左平移3格,把图形③向上平移4格。
37.如图,淘气画图表示的计算过程时,还缺少最后一步,请你帮他画完。
38.有一个物体从上面看到的形状如图所示,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,分别画出从前面和从左面看到的这个几何体的形状图。
39.画出下面轴对称图形的另一半,然后将这个轴对称图形向右平移8格。
40.要求:添加一个正方形,形成一个轴对称图形,并给出3种方案,画出对称轴。
41.画一条射线,正好把下面的直角平均分成两个度数相等的角。
42.下面是用4个小正方体搭成的立体图形,分别画出从上面、正面、左面看到的形状。
43.按要求画一画。
(1)请画出三角形先向下平移3格,再向右平移1格后的图形。
(2)如果每个小方格的边长是1厘米,请你画出一个面积为9平方厘米的正方形,再画出一个和它周长相等的长方形。
44.圈一圈,用两种方法表示7×9。
45.下面是乐乐和小强的对话,请根据他们的描述,画出路线示意图。
46.画图说明:等式两边都加上同一个数,等式仍然成立。
47.按分数圈一圈。
48.先画出如图的轴对称图形,再把整个图向右平移8格。
49.按要求画一画。
(1)以直线l为对称轴,画出图形A的轴对称图形B。
(2)将图形A先向下平移7格,再向右平移5格,得到图形C。
(3)将图形A绕点O顺时针旋转90°,得到图形D。
(4)将图形A按2∶1的比放大,画出放大后的图形E。
50.在下面每个转盘上按要求涂色。
使指针停在涂色区域 使指针停在空白区域 使指针停不可能停在
的可能性大,停在空 的可能性大,停在涂 空白区域上。
白区域的可能性小。 色区域的可能性小。
51.从给出的点画起,分别画一个直角、一个锐角、一个钝角。
52.用四种不同的方法在图中给1个小正方形涂色,使涂色部分成为轴对称图形。
53.笑笑对三(1)班30名同学用“平移”设计最喜欢的图案情况进行了调查,调查结果如下图。(一个○代表一人)
(1)设计小鱼图案的有( )人,占总人数的( )。
(2)笑笑在检查○个数时,发现与总人数不相符。她确定设计小鱼图案是12人没有错,设计汽车和房子图案的共有10人,设计( )图案的人数画错了,请你把它画正确。
54.按要求画一画。
(1)以虚线为对称轴,画出图形①的轴对称图形。
(2)将图形②绕点逆时针旋转。
(3)将图形②先向下平移6格,再向右平移3格。
(4)将图形③放大,使得放大后的图形与原图形对应线段长的比是。
55.观察下面的物体,分别画出从正面、上面、左面看到的立体图形的形状。
56.奇思在7-11岁每年的生日测得体重如下表。
年龄/岁 7 8 9 10 11
体重/千克 20 22 25 30 33
根据表中的数据,完成下面的折线统计图。
57.画一画。
(1)以虚线为对称轴,画出图形A的轴对称图形。
(2)把图形B先向右平移5格,再向上平移2格。
58.下图是轴对称图形,请你画出图形的另一半。
59.画2个面积是12平方厘米的长方形。(每一个小方格是1平方厘米)
60.用两种方法在点子图上表示8×6。
《小升初暑假专项提升测试卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
1.见详解
【分析】根据题意,明确连接两点间线段最短,所以从A到B直接连线即可。拿到球后,要想尽快离开球场,就要从B点到离B最近的边线处直线垂直方向跑出,从B点向上边的线画一条垂线,这样路线最短,速度最快。
【详解】根据分析画线如下:
最短路径就是“先从A点沿直线走到B点捡球,再从B点沿最短距离(垂直方向)到球场边线离开”。
2.见详解
【分析】梯形是只有一组对边平行的四边形,等腰直角三角形的两条腰相等,有一个直角。平行四边形是两组对边平行的四边形。据此画图。
【详解】
(答案不唯一)
3.见详解
【分析】把6个长方形平均分成3份,其中的一份就是这些长方形的。
把12个笑脸平均分成4份,其中的1份就是这些笑脸的。
【详解】
4.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出图形①的关键对称点,依次连接即可;根据平移的特征,把图形②的各顶点先向右平移6格,再向下平移3格,依次连接即可得到平移后的图形。
【详解】(1)(2)作图如下:
。
5.(1)(2)图见详解
【分析】(1)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点即可。
【详解】(1)(2)作图如下:
6.见详解
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。
【详解】
7.见详解
【分析】经过两点,有且只有一条直线,据此即可经过任意两点,先画出一条直线。
过另外一点画出这条直线的垂线方法如下:用三角板的一条直角边与所画的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和另一点重合,过这点沿直角边向已知直线画一条直线,并画上垂直符号,这条直线就是已知直线的垂线。
【详解】连接AC两点画一条直线,再过B点画出这条直线的垂线,如下图所示:(答案不唯一)
【点睛】本题考查过直线外一点作已知直线的垂线的方法,要熟练掌握。
8.见详解
【分析】两点之间线段最短,所以小猫去小兔家沿着小猫到小兔家的线段走路程最短;直线外一点到直线上各点的连线中,垂线段最短,所以从小兔家到河边沿着小兔家到河边的垂线短路程最短;据此即可解答。
【详解】
9.2
图见详解
【分析】测量物体长度时,将物体的一侧与直尺的0刻度线对齐,物体与直尺放平,不要倾斜,物体另一侧与直尺所对应的刻度就是物体的长度。由此量出线段的长度,再加上3厘米就是要画的线段长度。画线段时,先点上一个点,用直尺的0刻度线对齐这个点,找到要画的线段的刻度点上另一个点,沿着直尺连接两点,写上刻度即可。
【详解】测量填写如下:
2厘米
2+3=5(厘米)
10.图见详解;三角形
【分析】补全轴对称图形的方法:找出图形的关键点,依据轴对称图形的性质:对称点到对称轴的距离相等;根据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形;再根据画出的图形进行判断,说说它像什么。
【详解】作图如下:
它像一个三角形。
11.见详解
【分析】要使这个游戏对奇思和妙想都公平,那么2的倍数所占区域就要和5的倍数所占区域相同,由图可以看出每个扇形的面积相同,分别把它们平均分开,填写数字即可。
【详解】2的倍数可填2、4、6、8;
5的倍数可填5、15、25、35。
(答案不唯一)。
【点睛】本题考查游戏的公平性,要使游戏公平,就要使2的倍数和5的倍数出现的可能性一样大,它们所占的区域就要一样大。
12.(1)(2)见详解
【分析】(1)用图①里的小正方形的个数×35%,求出要涂的小正方形的个数,涂色;
(2)根据长方形的周长公式:周长=(长+宽)×2,长+宽=周长÷2,代入数据,求出长方形的长和宽的和,因为长和宽的比是5∶2,即长占长和宽的和的,宽占长和宽的,用长和宽的和×,求出长方形的长;用长和宽的和×,求出长方形的宽,画出长方形。
【详解】(1)5×4×35%
=20×35%
=7(格)
如下图(涂法不唯一):
(2)长:28÷2×
=14×
=10(厘米)
28÷2×
=14×
=4(厘米)
如下图(位置不唯一):
13.见详解
【分析】图形一:把正方形平均分成4份,其中的3份涂上颜色;
图形二:把全部☆平均分成4份,再把其中的3份圈起来。
【详解】
【点睛】熟练掌握分数的意义是解答此题的关键。
14.见详解
【分析】对称轴的画法:(1)找出轴对称图形的任意一组对称点。(2)连接对称点。(3)画出对称点所连线段的垂直平分线,就是该图形的对称轴,据此解答。
【详解】 (答案不唯一)
【点睛】本题考查对称轴的画法,理解轴对称图形的意义是本题的解题关键,注意要画虚线。
15.
【分析】观察前三支铅笔,方向依次顺时针旋转90°(第一支向右,第二支向下,第三支向左),所以第四支应继续顺时针旋转90°,即朝上,圆头在下。
【详解】
如图:
16.见详解
【分析】根据“上北下南,左西右东”,从“”开始,小山羊向东走2格,再向南走5格,最后向西走6格即可找到原来的位置。
【详解】如图:
17.见详解
【分析】任意摸一个球,摸到红球的可能性最大,白球次之,黑球的可能性最小;说明红球的数量最多,白球的数量排在第二,黑球的数量最少;则10个球中,可以涂5个红球、3个白球、2个黑球。
【详解】如下图:
(答案不唯一)
【点睛】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小。
18.(1)(2)(3)见详解
【分析】(1)将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,据此画出图形A的一条对称轴;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴a的右边画出左图的四个对称点,再首尾连接各点即可得到A的对称图形B;
(3)根据平移的特征,把图形B的四个顶点分别向下平移5格,再向左平移7格,再首尾连接各点,即可得到图形B平移后的图像C。
【详解】(1)(答案不唯一)、(2)、(3)见下图:
【点睛】本题考查画对称图形的对称轴,补全轴对称图形以及作平移后的图形。
19.见详解
【分析】从算式中可以得出,这个图形可以是底×高÷2,则这个直角三角形的底是(8+5)cm,高是5cm。据此作图即可。
【详解】(5+8)×5÷2
=14×5÷2
=35(cm2)
(画法不唯一)
20.见详解
【分析】0.6表示把整体1平均分成10份,其中的1份是0.1,有这样的6份,0.6×3表示有3个0.6,由此涂出3个0.6,然后根据所涂的阴影部分计算出结果;
0.06表示把整体1平均分成100份,其中的1份是0.01,有这样的6份,8×0.06表示有8个0.06,由此涂出8个0.06,然后根据所涂的阴影部分计算出结果。
【详解】
21.见详解
【分析】正方体展开图有11种特征,分四种类型,即第一种:“1-4-1”,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”,即每一行放2个正方形;第三种:“3-3”,即每一行放3个正方形;第四种:“1-3-2”,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。已知给出的两个平面图形可以看成是第一种“1-4-1”类型,即分别在两个平面图形的第二行添加1个小正方形,都能成为正方体的展开图。
【详解】如图所示:
22.(1)见详解
(2)53;故事书
(3)见详解
【分析】(1)根据四(一)班同学最喜欢的图书的情况统计表,在条形图的横坐标上标出各最喜欢的图书的种类,在纵坐标上标出人数,根据统计表中的数据,结合条形统计图的格数,一格表示3人比较合适,并在最喜欢的图书的种类对应的方格中涂色表示出人数即可。
(2)把最喜欢的各种图书人数相加,即可求出一共有多少名学生。把最喜欢的各种图书人数进行比较,找出喜欢的人数最多图书即可。
(3)把最喜欢的各种图书人数进行比较,即可得出结论。
【详解】(1)
(2)20+6+15+12
=26+15+12
=41+12
=53(名)
即一共有53名学生,
20>15>12>6
即喜欢故事书的同学最多。
(3)故事书买的最多,科技书和连环画买的基本一样多,漫画书买的最少。
我的想法是:喜欢故事书的人数最多,就买的最多,喜欢漫画的人数最少,则漫画书就买的最少。(答案不唯一)
23.(1)见详解
(2)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,以图形A右半图左边所在的虚线作对称轴,在对称轴的左边画出图A右半图的关键对称点,依次连接即可。
(2)根据平移的特征,把图B的各顶点分别向上平移3格,依次连接即可得到平移后的图形。
【详解】如图所示:
【点睛】本题主要考查轴对称图形和平移图形的画法,需熟练掌握。
24.见详解
【分析】根据垂线段的性质:从直线外一点向已知直线画垂线段和斜线,垂线段最短。把公路看作一条直线,A村看作一个点,由点向直线画垂线段即可。
【详解】
【点睛】本题主要考查垂线段的性质,利用这一性质作最短路线图。
25.见详解(画法不唯一)
【分析】等腰直角三角形:有两条边相等,并且有一个角是直角的三角形;梯形的定义:只有一组对边平行的四边形叫做梯形;平行四边形的定义:平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形;据此作图。
【详解】根据分析如图:
(画法不唯一)
26.见详解
【分析】根据不同的角度,观察立体图形,从正面可以看出,从下到上,第一行有三个小正方形,第二行有一个小正方形且在最左边;从上面看,从下到上,第一行有三个小正方形,第二行有一个小正方形且在最右边;从左面看,从下到上,第一行有两个小正方形,第二行有一个小正方形且在最右边。
【详解】如图:
【点睛】此题考查了从不同角度观察物体,培养了学生的空间想象力和抽象思维力。
27.(1)A(6,5);C(7,1)
(2)图见详解
(3)图见详解
【分析】(1)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,据此用数对表示点A和点C。
(2)根据梯形的面积公式:面积=(上底+下底)×高÷2,算式是(2+4)×4÷2,由此可知,梯形的上底是2厘米,下底是4厘米,高是4厘米;观察图形可知,点B到点C的距离是1×4=4厘米,点A到线段BC的距离是1×4=4厘米,BC为下底,点A到BC的距离为高,画出梯形;
(3)根据路程=速度×时间,用0.5×6=3厘米,计算出蚂蚁爬行的路程,根据地图上方向的规定“上北下南,左西右东”,确定出点E;计算出梯形面积,三角形面积等于梯形面积,根据三角形的面积公式:底×高÷2,确定出三角形的底和高,画出三角形即可。
【详解】(1)点A用数对表示为(6,5);点C用数对表示为(7,1)。
(2)BC=1×4=4(厘米)
如下图:
(3)0.5×6=3(厘米)
(2+4)×4÷2
=6×4÷2
=24÷2
=12(平方厘米)
三角形面积是12平方厘米,三角形的底是6厘米,高是4厘米;如下图:
(三角形画法不唯一)
28.见详解
【分析】用正负数表示意义相反的两种量,向东走为正,向西走为负,据此可知“﹢3米”表示从小树现在的位置向东走3米,即移动3格;“﹣7米”表示从走了“﹢3米”的位置再向西走7格;“﹢5米”表示从走了“﹣7米”之后的位置向东走5格,据此在图中表示出位置即可。
【详解】表示如下:
29.见详解。
【分析】轴对称图形的画法,先找准对称轴,结合轴对称图形的特点在对称轴的另一边画出图形的另一半即可,画好之后,由于图形平移前后图形的形状、大小和方向不变,只是位置发生改变,根据这一点画出平移后的图形即可。
【详解】依题意,结合所学知识作答如下:
【点睛】本题考查学生对轴对称图形的画法和理解以及图形平移的画法和理解
30.见详解
【分析】(1)把长方形平均分成4份,把其中1份涂色,涂色部分表示。
(2)把10个草莓平均分成5份,把其中3份涂色,涂色部分表示。
【详解】
31.见详解
【分析】把这18个圆看作一个整体,把它平均分成6份(1份3个),每份是它的,表示其中2份涂色;
把这9个五角星看作一个整体,把它平均分成3份(1份3个),每份是它的,表示其中1份涂色;据此解答即可。
【详解】据分析作图如下:
(答案不唯一)
32.见详解
【分析】根据小数除法的计算方法:①5.4÷5=a,把5.4看作5.5,因为5.5÷5=1.1,所以a的值应小于1.1但接近1;②4.01÷0.98=b,把4.01看作4,0.98看作1,因为4÷1=4,0.98小于1,则b的值大于4且接近4;③5÷1.05=c,把1.01看作1,5÷1=5,因为1.01大于1,则c的值小于5但接近5;据此解答。
【详解】a、b、c的大概位置如图所示:
33.见详解
【分析】钟面一周为360°,共分12大格,每大格为360÷12=30°,则
60°,时针和分针应相隔2个大格,时针指2,分针指12,画出时间是2:00;
90°,时针和分针应相隔3个大格,时针指3,分针指12,画出时间是3:00;
180°,时针和分针应相隔6个大格,时针指6,分针指12,画出时间是6:00;据此画图即可。
【详解】根据分析作图如下:
(60°、90°答案不唯一)
34.见详解(答案不唯一)
【分析】等腰三角形有两条边相等;两组对边分别平行且相等的四边形叫平行四边形;只有一组对边平行的四边形叫梯形。根据平行四边形和梯形的定义,即可解答。
【详解】如图:
35.见详解
【分析】由于光是沿直线传播的,视线也是如此,以欢欢的眼睛为点,过这个物体的两端画射线,物体后面(相对欢欢来说),两射线之间为欢欢的盲区,妹妹可以在这个范围内活动。
【详解】如图:
36.见详解
【分析】根据平移的特征,把图形①的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形;用同样的方法即可把图形②向左平移3格、图形③向上平移4格。
【详解】据分析作图如下:
37.见详解
【分析】根据图意,是把长方形平均分成了5份,取其中的4份;表示把平均分成3份,取其中的1份,据此画图表示即可。
【详解】计算过程画图如下:
【点睛】此题考查的是对分数乘分数的意义的理解;分数乘分数,表示的是求一个分数的几分之几是多少。
38.见详解
【分析】根据俯视图中,这个立体图形有前后2排,其中前面一排有一层两个小正方体,后面一排左边的有3个小正方体,右边的有2个小正方体。从前面看:图形有3层,第一层有3个小正方形,第二层有2个小正方形且靠右,第三层有1个小正方形位于中间;从左面看:有3层,第一层有2个小正方形,第二层有1个小正方形,第三层有1个小正方形,左边对齐。据此可得出答案。
【详解】
39.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可画出下面轴对称图形的另一半;根据平移的特征,把这个轴对称图形的各顶点分别向右平移8格,依次连接即可得到平移后的图形。
【详解】如图:
【点睛】作平移后的图形、作轴对称图形,对应点(对称点)位置的确定是关键。
40.见详解
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,从而可以画出对称轴图形。在图形的右上角添一个正方形,使得图形左右对称;在图形的左上角添一个正方形,使得图形沿45°对称;在图形的左下角添加一个正方形,使得图形上下对称。
【详解】如图:
【点睛】本题考查了轴对称图形的特点及灵活运用,并据此画出对称轴。
41.见详解
【分析】直角为90°,平分的话两个角都为90°÷2=45°,只需要用量角器画一个45°的角(在直角内部),画一条射线即可。
【详解】
42.见详解
【分析】观察图形可知,从正面看到的是2层:下层3个正方形,上层1个正方形居中;从上面看到的是2层:下层2个正方形,上层1个正方形靠右边的右面;从左面看到的图形是2层:下层2个正方形,上层1个正方形靠右边。
【详解】由分析作图如下:
【点睛】本题主要考查立体图形三视图的画法,意在培养学生的空间想象能力及动手操作能力。
43.(1)(2)图见详解
【分析】(1)作平移后的图形的方法:找出构成图形的关键点,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)正方形面积=边长×边长,3×3=9(平方厘米),面积为9平方厘米的正方形边长为3厘米,据此画出正方形;正方形周长=边长×4,3×4=12(厘米),长方形周长=(长+宽)×2,周长是12厘米则长+宽=12÷2=6(厘米),可以长为5厘米宽为1厘米,可以长为4厘米宽为2厘米,据此画出长方形即可。
【详解】
(1)(2)如图:
44.见详解
【分析】乘法算式7×9所表示的意义,就是7个9相加或9个7相加,即每行9个,共7行,或每行7个,共9行。据此画图即可。
【详解】根据分析作图如下:
【点睛】本题考查了学生利用画图理解乘法意义。
45.见详解
【分析】先依据题目条件得出图上距离1厘米表示实际距离50米,进而求出行走的图上距离,再据行走方向,即可画出符合要求的路线图。
以亮亮家为观测点画一个十字,然后正东方向找出1厘米。
再以新华书店为观测点画一个十字,然后按照这个方向画出图上3厘米,也就是150米。
最后再以购物广场为观测点,画一个十字,然后按照这个方向画出图上2厘米,也就是100米。
【详解】50÷50=1(厘米)
150÷50=3(厘米)
100÷50=2(厘米)
46.见详解;通过上图发现,天平的两边同时放入一个同样的东西,天平仍然平衡,所以等式两边都加上同一个数,等式仍然成立。
【分析】根据题意,可以通过画图的方式,先在天平两边各放一个同样的正方形,使天平平衡,再在天平的两边同时放入一个同样的圆形,天平仍然平衡。
【详解】根据分析可知:
答:通过上图发现,天平的两边同时放入一个同样的东西,天平仍然平衡,所以等式两边都加上同一个数,等式仍然成立。
(答案不唯一)
47.见详解
【分析】想要圈出题目中给出的分数,就要先把整体平均分成几个部分,然后每一部分就是几分之一,几个部分就是几分之几。
(1)把图中6个萝卜平均分成6份,每份是1个,圈出其中2个表示;
(2)把图中9条鱼平均分成9份,每份是1个,圈出其中5个表示;
(3)图中图形有4行,将图形平均分成4份,每份是1行,圈出其中1行表示;
(4)图中图形有5行和5列,将图形平均分成5份,每份是1行或者1列,圈出其中3行或3列表示。
【详解】圈一圈如下:
(答案不唯一)
48.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一侧画出原题的关键对称点,连接即可。
根据平移的特征,把图形的各个顶点向右平移8格,依次连接,即可得到平移后的图形。
【详解】
【点睛】本题考查了补全轴对称图形,作平移后的图形。掌握作图方法和步骤是解题的关键。
49.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴右边画出图形A的关键对称点,依次连接即可图形B;
(2)根据平移的特征,将图形A的各个顶点先向下平移7格,再向右平移5格,即可得到图形C;
(3)根据旋转的特征,图形A绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图D;
(4)根据图形放大的意义,放大后的图形是原图形对应线段长的2倍,底=2×2=4格;高=3×2=6格,画出放大后的图形。
【详解】(1)(2)(3)(4)如下图:
【点睛】本题考查的目的是理解掌握图形的旋转、平移、轴对称图形的性质及应用,图形放大的方法及应用。
50.见详解
【分析】转盘中哪种颜色区域越大,指针停在该颜色区域的可能性就越大,转盘中哪种颜色区域越小,指针停在该颜色区域的可能性就越小。
(l)使指针停在涂色区域的可能性大,停在空白区域的可能性小,则黑色区域的份数>白色区域的份数,转盘中黑色区域涂6份,白色区域有2份;
(2)使指针停在空白区域的可能性大,停在涂色区域的可能性小,则黑色区域的份数<白色区域的份数,转盘中黑色区域涂2份,白色区域有6份;
(3)使指针停不可能停在空白区域上,则全部涂成黑色。
【详解】如图:
【点睛】本题主要考查可能性的大小,根据事件发生可能性的大小确定各颜色区域的大小是解答题目的关键。
51.见详解
【分析】角有两条直直的边和一个公共端点,这两条直直的边叫做角的边,它们的公共端点叫做角的顶点;
三角板上最大的角就是直角,比直角小的角是锐角,比直角大的角是钝角。据此作图即可。
【详解】作图如下:
(画法不唯一)
52.见详解
【分析】根据轴对称图形的定义:把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴。分别进行涂色和画对称轴即可。注意:折叠之后的图形不止要涂色的部分重合,未涂色的部分也要重合,才是轴对称图形。
【详解】根据分析可知:
53.(1)12;;(2)树;图见详解
【分析】(1)数出小于上方对应圆的个数即为人数12人,总人数为30人,把30人平均分成30份,12人占了其中的12份,用分数表示;
(2)用总人数30人-设计小鱼图案是12人-设计汽车和房子图案的共有10人=8人,设计树图案的人数应有8人,图中只表示出5个圆即为5人,再画8-5=3个圆即可。
【详解】(1)由分析可知:设计小鱼图案的有12人,占总人数的;
(2)30-12-10
=18-10
=8(人)
8-5=3(人)
设计(树)图案的人数画错了;
54.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右面画出图①的关键对称点,依次连接即可;
(2)根据旋转的特征,图形②绕点A逆时针旋转90°,点A的位置不动,其余各部分绕此点按相同的方向旋转相同的度数即可画出旋转后的图形;
(3)根据平移的特征,把图形②的各顶点分别向下平移6格,再向右平移3格,依次连接即可得到平移后的图形;
(4)根据图形放大的意义,把图形③的各边均放大到原来的3倍,对应角大小不变,即可得到图形③按3∶1放大后的图形。
【详解】
【点睛】图形旋转、平移、轴对称大小不变,形状不变,改变的是位置或方向,图形放大或缩小,形状不变,改变的是大小。
55.见详解
【分析】观察图形可知,从正面看到的图形是3层,下层是2个正方形,中层是1个正方形,靠左边,上层是1个正方形,靠左边;从上面看到的图形是2层,下层是1个正方形,上层是2个正方形,靠左边;从左面看到的图形是3层,下层是2个正方形,中层是1个正方形,靠左边,上层是1个正方形,靠左边;由此即可画图。
【详解】如图:
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
56.见详解
【分析】图中纵轴一格表示10千克,将奇思每一年的体重分别在折线统计图上描出点,再将这些点依次连成线段即可得到折线图。
【详解】
57.(1)(2)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可。
(2)根据平移的特征,把图形B的各个顶点分别向右平移5格,再向上平移2格,依次连接,即可得平移后的图形。
【详解】(1)(2)如图:
58.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
【点睛】补全轴对称图形,确定图形的关键点及对称点是解决本题的关键。
59.见详解
【分析】根据长方形的面积公式:面积=长×宽。每一个小方格是1平方厘米,说明小方格的边长为1厘米。12可以分解成2×6、3×4,画出宽为2厘米,长为6厘米,或者宽为3厘米,长为4厘米的长方形,据此解答即可。
【详解】画图如下:
(答案不唯一)
【点睛】本题考查长方形的面积公式,长方形的面积已知,根据面积确定出长方形的长和宽的值,即可画出符合要求的长方形。
60.见详解
【分析】8×6可以表示:8个6的和是多少或6个8的和是多少;
所以,可以圈一行8个点,圈出6行;
也可以圈一行6个点,圈出8行。
【详解】由题意得:
用两种方法在点子图上表示8×6,如下图:
【点睛】此题主要考查的是点子图与乘法算式的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.王强在篮球场打球。现在处,他要先去点捡球再尽快离开球场。请帮他设计一条最快离开球场的线路,在图中画出来。
2.在点子图中按要求画图。
3.按分数圈一圈。
4.(1)画出以虚线为对称轴,图形①的另一半图形。
(2)画出图②向右平移6格,再向下平移3格的图形。
5.按要求画一画。
(1)画出图①先向右平移3格,再向下平移5格后的图形。
(2)以虚线a为对称轴,画出图②的轴对称图形。
6.找出下面轴对称图形的对称轴并画出来。
7.下面有3个点,连接其中两点画一条直线,再过另一点画出这条直线的垂线。
8.如图,小猫先去小兔家,然后它们一起到河边钓鱼,请帮小猫分别设计一条最近的路线。
9.先量出下面线段的长度,再画一条比它长3厘米的线段。
( )厘米
10.请你画出对称轴的另一半,并说一说像什么。
11.奇思和妙想用转盘玩数字游戏。如果指针指向2的倍数就是奇思获胜,如果指针指向5的倍数就是妙想获胜,请你在图上填上合适的数,使这个游戏对双方都公平。
12.下面每个小方格的边长都表示1厘米,按要求画一画,涂一涂。
(1)在图①中涂色表示。
(2)沿着方格线画一个周长是28厘米且长和宽的比是的长方形。
13.圈一圈或画一画,分别表示出下图中的。
14.画出下列轴对称图形的一条对称轴。
15.找规律,接着画。
( )
16.下图中,“”是小山羊向东走6格,再向北走5格,最后向西走2格后的位置,小山羊原来在哪里?在图中用“○”表示。
17.在下面的球中涂色,使任意摸一个球,摸到红球的可能性最大,白球次之,黑球的可能性最小。
18.(1)作出图形A的一条对称轴;
(2)以直线a为对称轴,作出图形A的轴对称图形B;
(3)将图形B向下平移5格,再向左平移7格,得到图形C。
19.如图,两个正方形拼接在一起,请你在图中设计一种能用算式:(5+8)×5÷2计算面积的图形,涂色表示出来。
20.涂一涂,填一填。
21.请你分别给下面的两个平面图形添加1个小正方形,使其都能成为正方体的展开图。
22.涂一涂,再回答问题。
下面是四(一)班同学最喜欢的图书的情况统计表。
类别 故事书 漫画书 科幻书 连环画
人数 20 6 15 12
(1)根据统计表画出条形统计图。
(2)一共有( )名学生,喜欢( )的同学最多。
(3)如果让你为班级买书,你怎么买?说说你的想法。
23.按要求画图。
(1)画出图A的另一半,使它成为一个以虚线为对称轴的轴对称图形。
(2)画出图B向上平移3格后的图形。
24.为振兴乡村,方便A村的人民出行,计划修一条通往公路的柏油路。怎样修路最近?请画出来。
25.在下面的方格纸上画一个等腰直角三角形,一个梯形和一个平行四边形。
26.想一想,分别画出下面立体图形从正面、上面和左面看到的形状。
27.下图中每个小方格的边长是1厘米。
(1)点A用数对表示是( , ),点C用数对表示是( , )。
(2)计算某梯形面积的算式是(2+4)×4÷2,根据这个算式在方格图中把以A、B、C为3个顶点的梯形画完整。
(3)一只蚂蚁每秒爬行0.5厘米,它从C点向正东方向爬行了6秒,到达点E,请以E点为一个顶点,画一个与上面的梯形面积相等的三角形。
28.奇思一开始站在小树的位置,他向东走用正数表示,向西走用负数表示。他先走了﹢3米,再走了﹣7米,最后又走了﹢5米。请你用▲分别标出他三次行走后到达的位置。(每段表示1米)
29.画出方格中图形的轴对称图形,再将画完整的图形向左平移3格。
30.根据分数涂色。
31.先按左边的分数圈一圈,再在圈出的图形上涂上你喜欢的颜色。
32.估一估,分别在下图中标出a、b、c的大概位置。
5.4÷5=a 4.01÷0.98=b 5÷1.05=c
33.在钟面上画出时针和分针表示整时,并让它们所成的角等于给定的度数。
34.在方格纸上画出等腰三角形、梯形和平行四边形各一个。
35.欢欢和妹妹在院子里玩“看不看得见”的游戏,欢欢站在墙的一侧不动,妹妹在墙的另一侧活动,为了不让欢欢看见妹妹,请你画出妹妹可以活动的区域。
36.操作题。
移一移,描一描。
把图形①向右平移4格,把图形②向左平移3格,把图形③向上平移4格。
37.如图,淘气画图表示的计算过程时,还缺少最后一步,请你帮他画完。
38.有一个物体从上面看到的形状如图所示,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,分别画出从前面和从左面看到的这个几何体的形状图。
39.画出下面轴对称图形的另一半,然后将这个轴对称图形向右平移8格。
40.要求:添加一个正方形,形成一个轴对称图形,并给出3种方案,画出对称轴。
41.画一条射线,正好把下面的直角平均分成两个度数相等的角。
42.下面是用4个小正方体搭成的立体图形,分别画出从上面、正面、左面看到的形状。
43.按要求画一画。
(1)请画出三角形先向下平移3格,再向右平移1格后的图形。
(2)如果每个小方格的边长是1厘米,请你画出一个面积为9平方厘米的正方形,再画出一个和它周长相等的长方形。
44.圈一圈,用两种方法表示7×9。
45.下面是乐乐和小强的对话,请根据他们的描述,画出路线示意图。
46.画图说明:等式两边都加上同一个数,等式仍然成立。
47.按分数圈一圈。
48.先画出如图的轴对称图形,再把整个图向右平移8格。
49.按要求画一画。
(1)以直线l为对称轴,画出图形A的轴对称图形B。
(2)将图形A先向下平移7格,再向右平移5格,得到图形C。
(3)将图形A绕点O顺时针旋转90°,得到图形D。
(4)将图形A按2∶1的比放大,画出放大后的图形E。
50.在下面每个转盘上按要求涂色。
使指针停在涂色区域 使指针停在空白区域 使指针停不可能停在
的可能性大,停在空 的可能性大,停在涂 空白区域上。
白区域的可能性小。 色区域的可能性小。
51.从给出的点画起,分别画一个直角、一个锐角、一个钝角。
52.用四种不同的方法在图中给1个小正方形涂色,使涂色部分成为轴对称图形。
53.笑笑对三(1)班30名同学用“平移”设计最喜欢的图案情况进行了调查,调查结果如下图。(一个○代表一人)
(1)设计小鱼图案的有( )人,占总人数的( )。
(2)笑笑在检查○个数时,发现与总人数不相符。她确定设计小鱼图案是12人没有错,设计汽车和房子图案的共有10人,设计( )图案的人数画错了,请你把它画正确。
54.按要求画一画。
(1)以虚线为对称轴,画出图形①的轴对称图形。
(2)将图形②绕点逆时针旋转。
(3)将图形②先向下平移6格,再向右平移3格。
(4)将图形③放大,使得放大后的图形与原图形对应线段长的比是。
55.观察下面的物体,分别画出从正面、上面、左面看到的立体图形的形状。
56.奇思在7-11岁每年的生日测得体重如下表。
年龄/岁 7 8 9 10 11
体重/千克 20 22 25 30 33
根据表中的数据,完成下面的折线统计图。
57.画一画。
(1)以虚线为对称轴,画出图形A的轴对称图形。
(2)把图形B先向右平移5格,再向上平移2格。
58.下图是轴对称图形,请你画出图形的另一半。
59.画2个面积是12平方厘米的长方形。(每一个小方格是1平方厘米)
60.用两种方法在点子图上表示8×6。
《小升初暑假专项提升测试卷:作图题(含解析)-2024-2025学年下学期小学数学北师大版》参考答案
1.见详解
【分析】根据题意,明确连接两点间线段最短,所以从A到B直接连线即可。拿到球后,要想尽快离开球场,就要从B点到离B最近的边线处直线垂直方向跑出,从B点向上边的线画一条垂线,这样路线最短,速度最快。
【详解】根据分析画线如下:
最短路径就是“先从A点沿直线走到B点捡球,再从B点沿最短距离(垂直方向)到球场边线离开”。
2.见详解
【分析】梯形是只有一组对边平行的四边形,等腰直角三角形的两条腰相等,有一个直角。平行四边形是两组对边平行的四边形。据此画图。
【详解】
(答案不唯一)
3.见详解
【分析】把6个长方形平均分成3份,其中的一份就是这些长方形的。
把12个笑脸平均分成4份,其中的1份就是这些笑脸的。
【详解】
4.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线)的右边画出图形①的关键对称点,依次连接即可;根据平移的特征,把图形②的各顶点先向右平移6格,再向下平移3格,依次连接即可得到平移后的图形。
【详解】(1)(2)作图如下:
。
5.(1)(2)图见详解
【分析】(1)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形的各顶点关于对称轴的对称点后,依次连接各点即可。
【详解】(1)(2)作图如下:
6.见详解
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。
【详解】
7.见详解
【分析】经过两点,有且只有一条直线,据此即可经过任意两点,先画出一条直线。
过另外一点画出这条直线的垂线方法如下:用三角板的一条直角边与所画的已知直线重合,沿重合的直线平移三角板,使三角板的另一条直角边和另一点重合,过这点沿直角边向已知直线画一条直线,并画上垂直符号,这条直线就是已知直线的垂线。
【详解】连接AC两点画一条直线,再过B点画出这条直线的垂线,如下图所示:(答案不唯一)
【点睛】本题考查过直线外一点作已知直线的垂线的方法,要熟练掌握。
8.见详解
【分析】两点之间线段最短,所以小猫去小兔家沿着小猫到小兔家的线段走路程最短;直线外一点到直线上各点的连线中,垂线段最短,所以从小兔家到河边沿着小兔家到河边的垂线短路程最短;据此即可解答。
【详解】
9.2
图见详解
【分析】测量物体长度时,将物体的一侧与直尺的0刻度线对齐,物体与直尺放平,不要倾斜,物体另一侧与直尺所对应的刻度就是物体的长度。由此量出线段的长度,再加上3厘米就是要画的线段长度。画线段时,先点上一个点,用直尺的0刻度线对齐这个点,找到要画的线段的刻度点上另一个点,沿着直尺连接两点,写上刻度即可。
【详解】测量填写如下:
2厘米
2+3=5(厘米)
10.图见详解;三角形
【分析】补全轴对称图形的方法:找出图形的关键点,依据轴对称图形的性质:对称点到对称轴的距离相等;根据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形;再根据画出的图形进行判断,说说它像什么。
【详解】作图如下:
它像一个三角形。
11.见详解
【分析】要使这个游戏对奇思和妙想都公平,那么2的倍数所占区域就要和5的倍数所占区域相同,由图可以看出每个扇形的面积相同,分别把它们平均分开,填写数字即可。
【详解】2的倍数可填2、4、6、8;
5的倍数可填5、15、25、35。
(答案不唯一)。
【点睛】本题考查游戏的公平性,要使游戏公平,就要使2的倍数和5的倍数出现的可能性一样大,它们所占的区域就要一样大。
12.(1)(2)见详解
【分析】(1)用图①里的小正方形的个数×35%,求出要涂的小正方形的个数,涂色;
(2)根据长方形的周长公式:周长=(长+宽)×2,长+宽=周长÷2,代入数据,求出长方形的长和宽的和,因为长和宽的比是5∶2,即长占长和宽的和的,宽占长和宽的,用长和宽的和×,求出长方形的长;用长和宽的和×,求出长方形的宽,画出长方形。
【详解】(1)5×4×35%
=20×35%
=7(格)
如下图(涂法不唯一):
(2)长:28÷2×
=14×
=10(厘米)
28÷2×
=14×
=4(厘米)
如下图(位置不唯一):
13.见详解
【分析】图形一:把正方形平均分成4份,其中的3份涂上颜色;
图形二:把全部☆平均分成4份,再把其中的3份圈起来。
【详解】
【点睛】熟练掌握分数的意义是解答此题的关键。
14.见详解
【分析】对称轴的画法:(1)找出轴对称图形的任意一组对称点。(2)连接对称点。(3)画出对称点所连线段的垂直平分线,就是该图形的对称轴,据此解答。
【详解】 (答案不唯一)
【点睛】本题考查对称轴的画法,理解轴对称图形的意义是本题的解题关键,注意要画虚线。
15.
【分析】观察前三支铅笔,方向依次顺时针旋转90°(第一支向右,第二支向下,第三支向左),所以第四支应继续顺时针旋转90°,即朝上,圆头在下。
【详解】
如图:
16.见详解
【分析】根据“上北下南,左西右东”,从“”开始,小山羊向东走2格,再向南走5格,最后向西走6格即可找到原来的位置。
【详解】如图:
17.见详解
【分析】任意摸一个球,摸到红球的可能性最大,白球次之,黑球的可能性最小;说明红球的数量最多,白球的数量排在第二,黑球的数量最少;则10个球中,可以涂5个红球、3个白球、2个黑球。
【详解】如下图:
(答案不唯一)
【点睛】可以直接根据球的数量的多少来判断,数量多的摸到的可能性就大,数量少的摸到的可能性就小。
18.(1)(2)(3)见详解
【分析】(1)将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,据此画出图形A的一条对称轴;
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴a的右边画出左图的四个对称点,再首尾连接各点即可得到A的对称图形B;
(3)根据平移的特征,把图形B的四个顶点分别向下平移5格,再向左平移7格,再首尾连接各点,即可得到图形B平移后的图像C。
【详解】(1)(答案不唯一)、(2)、(3)见下图:
【点睛】本题考查画对称图形的对称轴,补全轴对称图形以及作平移后的图形。
19.见详解
【分析】从算式中可以得出,这个图形可以是底×高÷2,则这个直角三角形的底是(8+5)cm,高是5cm。据此作图即可。
【详解】(5+8)×5÷2
=14×5÷2
=35(cm2)
(画法不唯一)
20.见详解
【分析】0.6表示把整体1平均分成10份,其中的1份是0.1,有这样的6份,0.6×3表示有3个0.6,由此涂出3个0.6,然后根据所涂的阴影部分计算出结果;
0.06表示把整体1平均分成100份,其中的1份是0.01,有这样的6份,8×0.06表示有8个0.06,由此涂出8个0.06,然后根据所涂的阴影部分计算出结果。
【详解】
21.见详解
【分析】正方体展开图有11种特征,分四种类型,即第一种:“1-4-1”,即第一行放1个,第二行放4个,第三行放1个;第二种:“2-2-2”,即每一行放2个正方形;第三种:“3-3”,即每一行放3个正方形;第四种:“1-3-2”,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形。已知给出的两个平面图形可以看成是第一种“1-4-1”类型,即分别在两个平面图形的第二行添加1个小正方形,都能成为正方体的展开图。
【详解】如图所示:
22.(1)见详解
(2)53;故事书
(3)见详解
【分析】(1)根据四(一)班同学最喜欢的图书的情况统计表,在条形图的横坐标上标出各最喜欢的图书的种类,在纵坐标上标出人数,根据统计表中的数据,结合条形统计图的格数,一格表示3人比较合适,并在最喜欢的图书的种类对应的方格中涂色表示出人数即可。
(2)把最喜欢的各种图书人数相加,即可求出一共有多少名学生。把最喜欢的各种图书人数进行比较,找出喜欢的人数最多图书即可。
(3)把最喜欢的各种图书人数进行比较,即可得出结论。
【详解】(1)
(2)20+6+15+12
=26+15+12
=41+12
=53(名)
即一共有53名学生,
20>15>12>6
即喜欢故事书的同学最多。
(3)故事书买的最多,科技书和连环画买的基本一样多,漫画书买的最少。
我的想法是:喜欢故事书的人数最多,就买的最多,喜欢漫画的人数最少,则漫画书就买的最少。(答案不唯一)
23.(1)见详解
(2)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,以图形A右半图左边所在的虚线作对称轴,在对称轴的左边画出图A右半图的关键对称点,依次连接即可。
(2)根据平移的特征,把图B的各顶点分别向上平移3格,依次连接即可得到平移后的图形。
【详解】如图所示:
【点睛】本题主要考查轴对称图形和平移图形的画法,需熟练掌握。
24.见详解
【分析】根据垂线段的性质:从直线外一点向已知直线画垂线段和斜线,垂线段最短。把公路看作一条直线,A村看作一个点,由点向直线画垂线段即可。
【详解】
【点睛】本题主要考查垂线段的性质,利用这一性质作最短路线图。
25.见详解(画法不唯一)
【分析】等腰直角三角形:有两条边相等,并且有一个角是直角的三角形;梯形的定义:只有一组对边平行的四边形叫做梯形;平行四边形的定义:平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形;据此作图。
【详解】根据分析如图:
(画法不唯一)
26.见详解
【分析】根据不同的角度,观察立体图形,从正面可以看出,从下到上,第一行有三个小正方形,第二行有一个小正方形且在最左边;从上面看,从下到上,第一行有三个小正方形,第二行有一个小正方形且在最右边;从左面看,从下到上,第一行有两个小正方形,第二行有一个小正方形且在最右边。
【详解】如图:
【点睛】此题考查了从不同角度观察物体,培养了学生的空间想象力和抽象思维力。
27.(1)A(6,5);C(7,1)
(2)图见详解
(3)图见详解
【分析】(1)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,据此用数对表示点A和点C。
(2)根据梯形的面积公式:面积=(上底+下底)×高÷2,算式是(2+4)×4÷2,由此可知,梯形的上底是2厘米,下底是4厘米,高是4厘米;观察图形可知,点B到点C的距离是1×4=4厘米,点A到线段BC的距离是1×4=4厘米,BC为下底,点A到BC的距离为高,画出梯形;
(3)根据路程=速度×时间,用0.5×6=3厘米,计算出蚂蚁爬行的路程,根据地图上方向的规定“上北下南,左西右东”,确定出点E;计算出梯形面积,三角形面积等于梯形面积,根据三角形的面积公式:底×高÷2,确定出三角形的底和高,画出三角形即可。
【详解】(1)点A用数对表示为(6,5);点C用数对表示为(7,1)。
(2)BC=1×4=4(厘米)
如下图:
(3)0.5×6=3(厘米)
(2+4)×4÷2
=6×4÷2
=24÷2
=12(平方厘米)
三角形面积是12平方厘米,三角形的底是6厘米,高是4厘米;如下图:
(三角形画法不唯一)
28.见详解
【分析】用正负数表示意义相反的两种量,向东走为正,向西走为负,据此可知“﹢3米”表示从小树现在的位置向东走3米,即移动3格;“﹣7米”表示从走了“﹢3米”的位置再向西走7格;“﹢5米”表示从走了“﹣7米”之后的位置向东走5格,据此在图中表示出位置即可。
【详解】表示如下:
29.见详解。
【分析】轴对称图形的画法,先找准对称轴,结合轴对称图形的特点在对称轴的另一边画出图形的另一半即可,画好之后,由于图形平移前后图形的形状、大小和方向不变,只是位置发生改变,根据这一点画出平移后的图形即可。
【详解】依题意,结合所学知识作答如下:
【点睛】本题考查学生对轴对称图形的画法和理解以及图形平移的画法和理解
30.见详解
【分析】(1)把长方形平均分成4份,把其中1份涂色,涂色部分表示。
(2)把10个草莓平均分成5份,把其中3份涂色,涂色部分表示。
【详解】
31.见详解
【分析】把这18个圆看作一个整体,把它平均分成6份(1份3个),每份是它的,表示其中2份涂色;
把这9个五角星看作一个整体,把它平均分成3份(1份3个),每份是它的,表示其中1份涂色;据此解答即可。
【详解】据分析作图如下:
(答案不唯一)
32.见详解
【分析】根据小数除法的计算方法:①5.4÷5=a,把5.4看作5.5,因为5.5÷5=1.1,所以a的值应小于1.1但接近1;②4.01÷0.98=b,把4.01看作4,0.98看作1,因为4÷1=4,0.98小于1,则b的值大于4且接近4;③5÷1.05=c,把1.01看作1,5÷1=5,因为1.01大于1,则c的值小于5但接近5;据此解答。
【详解】a、b、c的大概位置如图所示:
33.见详解
【分析】钟面一周为360°,共分12大格,每大格为360÷12=30°,则
60°,时针和分针应相隔2个大格,时针指2,分针指12,画出时间是2:00;
90°,时针和分针应相隔3个大格,时针指3,分针指12,画出时间是3:00;
180°,时针和分针应相隔6个大格,时针指6,分针指12,画出时间是6:00;据此画图即可。
【详解】根据分析作图如下:
(60°、90°答案不唯一)
34.见详解(答案不唯一)
【分析】等腰三角形有两条边相等;两组对边分别平行且相等的四边形叫平行四边形;只有一组对边平行的四边形叫梯形。根据平行四边形和梯形的定义,即可解答。
【详解】如图:
35.见详解
【分析】由于光是沿直线传播的,视线也是如此,以欢欢的眼睛为点,过这个物体的两端画射线,物体后面(相对欢欢来说),两射线之间为欢欢的盲区,妹妹可以在这个范围内活动。
【详解】如图:
36.见详解
【分析】根据平移的特征,把图形①的各顶点分别向右平移4格,依次连接即可得到向右平移4格后的图形;用同样的方法即可把图形②向左平移3格、图形③向上平移4格。
【详解】据分析作图如下:
37.见详解
【分析】根据图意,是把长方形平均分成了5份,取其中的4份;表示把平均分成3份,取其中的1份,据此画图表示即可。
【详解】计算过程画图如下:
【点睛】此题考查的是对分数乘分数的意义的理解;分数乘分数,表示的是求一个分数的几分之几是多少。
38.见详解
【分析】根据俯视图中,这个立体图形有前后2排,其中前面一排有一层两个小正方体,后面一排左边的有3个小正方体,右边的有2个小正方体。从前面看:图形有3层,第一层有3个小正方形,第二层有2个小正方形且靠右,第三层有1个小正方形位于中间;从左面看:有3层,第一层有2个小正方形,第二层有1个小正方形,第三层有1个小正方形,左边对齐。据此可得出答案。
【详解】
39.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出左半图的关键对称点,依次连接即可画出下面轴对称图形的另一半;根据平移的特征,把这个轴对称图形的各顶点分别向右平移8格,依次连接即可得到平移后的图形。
【详解】如图:
【点睛】作平移后的图形、作轴对称图形,对应点(对称点)位置的确定是关键。
40.见详解
【分析】依据轴对称图形的概念,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,从而可以画出对称轴图形。在图形的右上角添一个正方形,使得图形左右对称;在图形的左上角添一个正方形,使得图形沿45°对称;在图形的左下角添加一个正方形,使得图形上下对称。
【详解】如图:
【点睛】本题考查了轴对称图形的特点及灵活运用,并据此画出对称轴。
41.见详解
【分析】直角为90°,平分的话两个角都为90°÷2=45°,只需要用量角器画一个45°的角(在直角内部),画一条射线即可。
【详解】
42.见详解
【分析】观察图形可知,从正面看到的是2层:下层3个正方形,上层1个正方形居中;从上面看到的是2层:下层2个正方形,上层1个正方形靠右边的右面;从左面看到的图形是2层:下层2个正方形,上层1个正方形靠右边。
【详解】由分析作图如下:
【点睛】本题主要考查立体图形三视图的画法,意在培养学生的空间想象能力及动手操作能力。
43.(1)(2)图见详解
【分析】(1)作平移后的图形的方法:找出构成图形的关键点,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(2)正方形面积=边长×边长,3×3=9(平方厘米),面积为9平方厘米的正方形边长为3厘米,据此画出正方形;正方形周长=边长×4,3×4=12(厘米),长方形周长=(长+宽)×2,周长是12厘米则长+宽=12÷2=6(厘米),可以长为5厘米宽为1厘米,可以长为4厘米宽为2厘米,据此画出长方形即可。
【详解】
(1)(2)如图:
44.见详解
【分析】乘法算式7×9所表示的意义,就是7个9相加或9个7相加,即每行9个,共7行,或每行7个,共9行。据此画图即可。
【详解】根据分析作图如下:
【点睛】本题考查了学生利用画图理解乘法意义。
45.见详解
【分析】先依据题目条件得出图上距离1厘米表示实际距离50米,进而求出行走的图上距离,再据行走方向,即可画出符合要求的路线图。
以亮亮家为观测点画一个十字,然后正东方向找出1厘米。
再以新华书店为观测点画一个十字,然后按照这个方向画出图上3厘米,也就是150米。
最后再以购物广场为观测点,画一个十字,然后按照这个方向画出图上2厘米,也就是100米。
【详解】50÷50=1(厘米)
150÷50=3(厘米)
100÷50=2(厘米)
46.见详解;通过上图发现,天平的两边同时放入一个同样的东西,天平仍然平衡,所以等式两边都加上同一个数,等式仍然成立。
【分析】根据题意,可以通过画图的方式,先在天平两边各放一个同样的正方形,使天平平衡,再在天平的两边同时放入一个同样的圆形,天平仍然平衡。
【详解】根据分析可知:
答:通过上图发现,天平的两边同时放入一个同样的东西,天平仍然平衡,所以等式两边都加上同一个数,等式仍然成立。
(答案不唯一)
47.见详解
【分析】想要圈出题目中给出的分数,就要先把整体平均分成几个部分,然后每一部分就是几分之一,几个部分就是几分之几。
(1)把图中6个萝卜平均分成6份,每份是1个,圈出其中2个表示;
(2)把图中9条鱼平均分成9份,每份是1个,圈出其中5个表示;
(3)图中图形有4行,将图形平均分成4份,每份是1行,圈出其中1行表示;
(4)图中图形有5行和5列,将图形平均分成5份,每份是1行或者1列,圈出其中3行或3列表示。
【详解】圈一圈如下:
(答案不唯一)
48.见详解
【分析】根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一侧画出原题的关键对称点,连接即可。
根据平移的特征,把图形的各个顶点向右平移8格,依次连接,即可得到平移后的图形。
【详解】
【点睛】本题考查了补全轴对称图形,作平移后的图形。掌握作图方法和步骤是解题的关键。
49.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴右边画出图形A的关键对称点,依次连接即可图形B;
(2)根据平移的特征,将图形A的各个顶点先向下平移7格,再向右平移5格,即可得到图形C;
(3)根据旋转的特征,图形A绕点O逆时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图D;
(4)根据图形放大的意义,放大后的图形是原图形对应线段长的2倍,底=2×2=4格;高=3×2=6格,画出放大后的图形。
【详解】(1)(2)(3)(4)如下图:
【点睛】本题考查的目的是理解掌握图形的旋转、平移、轴对称图形的性质及应用,图形放大的方法及应用。
50.见详解
【分析】转盘中哪种颜色区域越大,指针停在该颜色区域的可能性就越大,转盘中哪种颜色区域越小,指针停在该颜色区域的可能性就越小。
(l)使指针停在涂色区域的可能性大,停在空白区域的可能性小,则黑色区域的份数>白色区域的份数,转盘中黑色区域涂6份,白色区域有2份;
(2)使指针停在空白区域的可能性大,停在涂色区域的可能性小,则黑色区域的份数<白色区域的份数,转盘中黑色区域涂2份,白色区域有6份;
(3)使指针停不可能停在空白区域上,则全部涂成黑色。
【详解】如图:
【点睛】本题主要考查可能性的大小,根据事件发生可能性的大小确定各颜色区域的大小是解答题目的关键。
51.见详解
【分析】角有两条直直的边和一个公共端点,这两条直直的边叫做角的边,它们的公共端点叫做角的顶点;
三角板上最大的角就是直角,比直角小的角是锐角,比直角大的角是钝角。据此作图即可。
【详解】作图如下:
(画法不唯一)
52.见详解
【分析】根据轴对称图形的定义:把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴。分别进行涂色和画对称轴即可。注意:折叠之后的图形不止要涂色的部分重合,未涂色的部分也要重合,才是轴对称图形。
【详解】根据分析可知:
53.(1)12;;(2)树;图见详解
【分析】(1)数出小于上方对应圆的个数即为人数12人,总人数为30人,把30人平均分成30份,12人占了其中的12份,用分数表示;
(2)用总人数30人-设计小鱼图案是12人-设计汽车和房子图案的共有10人=8人,设计树图案的人数应有8人,图中只表示出5个圆即为5人,再画8-5=3个圆即可。
【详解】(1)由分析可知:设计小鱼图案的有12人,占总人数的;
(2)30-12-10
=18-10
=8(人)
8-5=3(人)
设计(树)图案的人数画错了;
54.(1)(2)(3)(4)见详解
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右面画出图①的关键对称点,依次连接即可;
(2)根据旋转的特征,图形②绕点A逆时针旋转90°,点A的位置不动,其余各部分绕此点按相同的方向旋转相同的度数即可画出旋转后的图形;
(3)根据平移的特征,把图形②的各顶点分别向下平移6格,再向右平移3格,依次连接即可得到平移后的图形;
(4)根据图形放大的意义,把图形③的各边均放大到原来的3倍,对应角大小不变,即可得到图形③按3∶1放大后的图形。
【详解】
【点睛】图形旋转、平移、轴对称大小不变,形状不变,改变的是位置或方向,图形放大或缩小,形状不变,改变的是大小。
55.见详解
【分析】观察图形可知,从正面看到的图形是3层,下层是2个正方形,中层是1个正方形,靠左边,上层是1个正方形,靠左边;从上面看到的图形是2层,下层是1个正方形,上层是2个正方形,靠左边;从左面看到的图形是3层,下层是2个正方形,中层是1个正方形,靠左边,上层是1个正方形,靠左边;由此即可画图。
【详解】如图:
【点睛】本题是考查从不同方向观察物体和几何体以及三视图的画法,目的是训练学生的观察能力。
56.见详解
【分析】图中纵轴一格表示10千克,将奇思每一年的体重分别在折线统计图上描出点,再将这些点依次连成线段即可得到折线图。
【详解】
57.(1)(2)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出原半图的关键对称点,依次连接即可。
(2)根据平移的特征,把图形B的各个顶点分别向右平移5格,再向上平移2格,依次连接,即可得平移后的图形。
【详解】(1)(2)如图:
58.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
【点睛】补全轴对称图形,确定图形的关键点及对称点是解决本题的关键。
59.见详解
【分析】根据长方形的面积公式:面积=长×宽。每一个小方格是1平方厘米,说明小方格的边长为1厘米。12可以分解成2×6、3×4,画出宽为2厘米,长为6厘米,或者宽为3厘米,长为4厘米的长方形,据此解答即可。
【详解】画图如下:
(答案不唯一)
【点睛】本题考查长方形的面积公式,长方形的面积已知,根据面积确定出长方形的长和宽的值,即可画出符合要求的长方形。
60.见详解
【分析】8×6可以表示:8个6的和是多少或6个8的和是多少;
所以,可以圈一行8个点,圈出6行;
也可以圈一行6个点,圈出8行。
【详解】由题意得:
用两种方法在点子图上表示8×6,如下图:
【点睛】此题主要考查的是点子图与乘法算式的关系。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
