第22章 相似形综合测试题(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
第22章 相似形综合测试题
一、单选题
1.(2020九上·江阴月考)如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是( )
A. B. C. D.
2.(2025九下·和平开学考)如图,点D,E分别在的边,上,且.,若,,则( )
A.9 B.8 C.6 D.4.5
3.(2025九下·潮南月考)如图,在平面直角坐标系中,为的边上一点,,过作交于点,、两点纵坐标分别为1、3,则点的纵坐标为( )
A.4 B.5 C.6 D.7
4.(2023·开远模拟)如图.在中,,若,则等于( )
A. B. C. D.
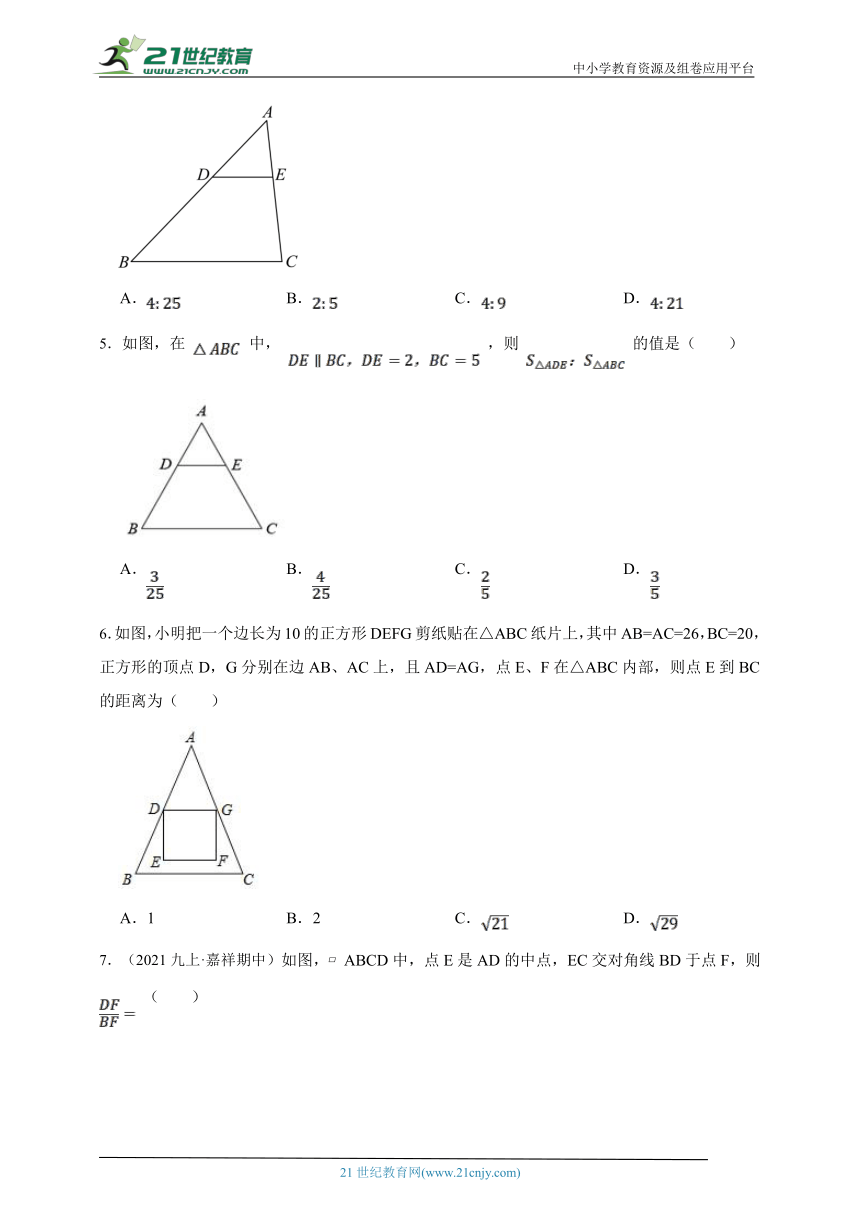
5.如图,在 中, ,则 的值是( )
A. B. C. D.
6.如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
A.1 B.2 C. D.
7.(2021九上·嘉祥期中)如图, ABCD中,点E是AD的中点,EC交对角线BD于点F,则 ( )
A. B.2 C. D.
8.(2023九上·襄都期中)已知线段,如果,那么下列各式一定正确的是( )
A. B. C. D.
9.(2021九上·温州期末)如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( )
A. B. C. D.
10.(2024·杭州模拟)如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论正确的是( )
A.OA2=OE OP B.OQ2=OA OF
C.若BP=1,则OE=2 D.若BP=1,则
二、填空题
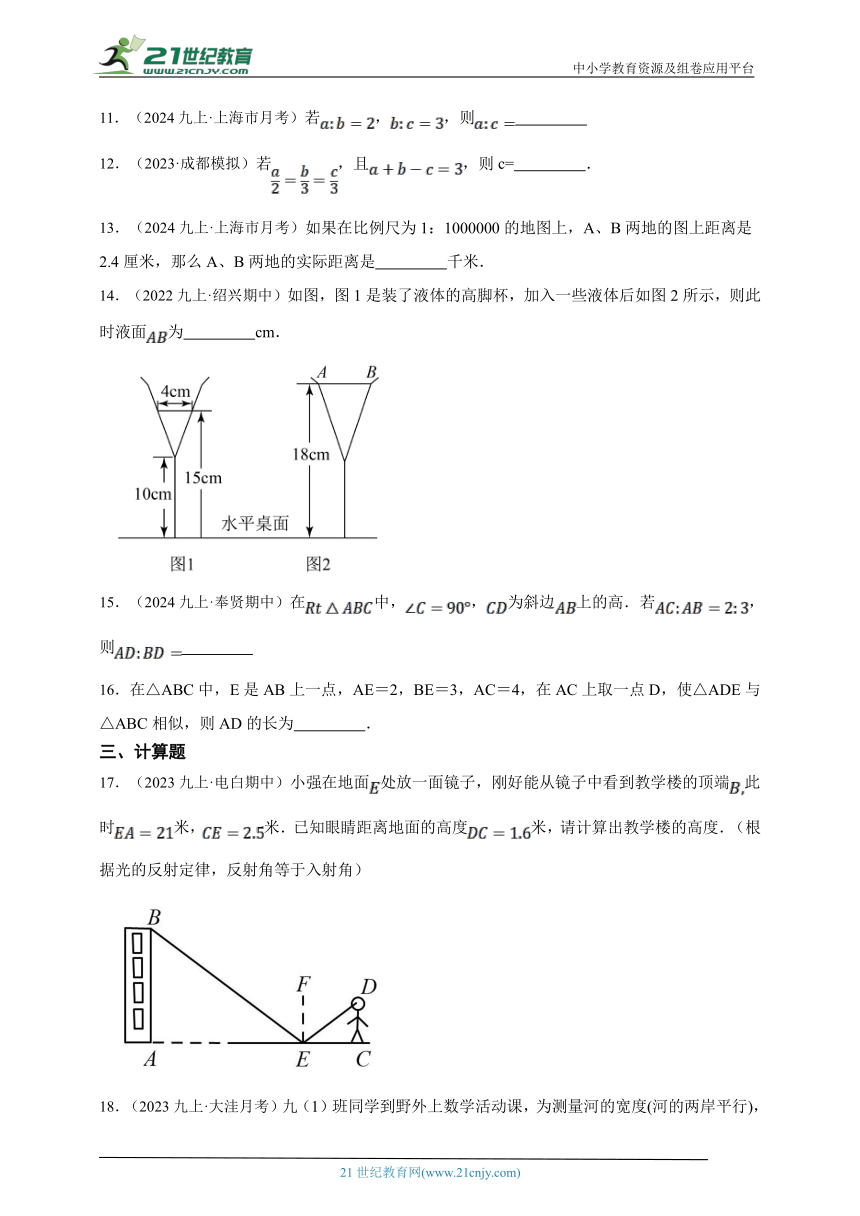
11.(2024九上·上海市月考)若,,则
12.(2023·成都模拟)若,且,则c= .
13.(2024九上·上海市月考)如果在比例尺为1:1000000的地图上,A、B两地的图上距离是2.4厘米,那么A、B两地的实际距离是 千米.
14.(2022九上·绍兴期中)如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面为 cm.
15.(2024九上·奉贤期中)在中,,为斜边上的高.若,则
16.在△ABC中,E是AB上一点,AE=2,BE=3,AC=4,在AC上取一点D,使△ADE与△ABC相似,则AD的长为 .
三、计算题
17.(2023九上·电白期中)小强在地面处放一面镜子,刚好能从镜子中看到教学楼的顶端此时米,米.已知眼睛距离地面的高度米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
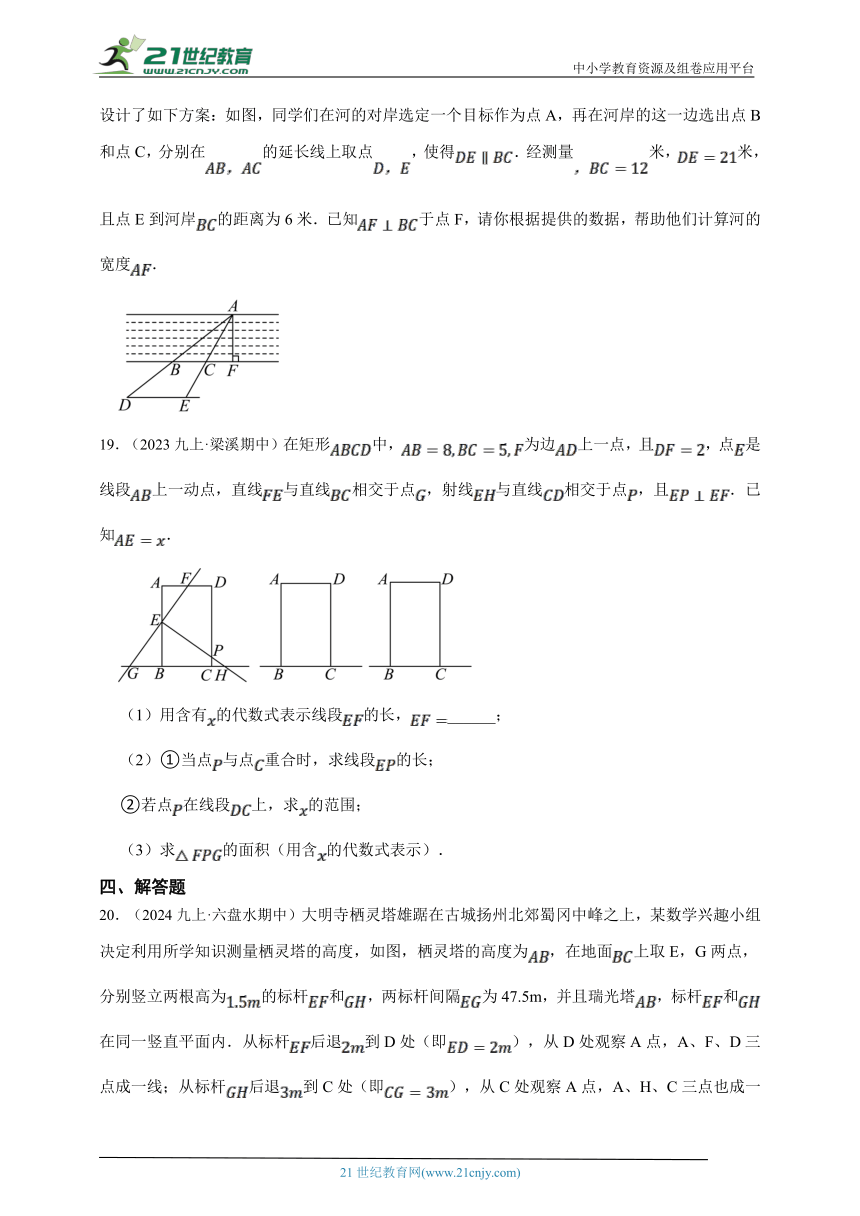
18.(2023九上·大洼月考)九(1)班同学到野外上数学活动课,为测量河的宽度(河的两岸平行),设计了如下方案:如图,同学们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量米,米,且点E到河岸的距离为6米.已知于点F,请你根据提供的数据,帮助他们计算河的宽度.
19.(2023九上·梁溪期中)在矩形中,为边上一点,且,点是线段上一动点,直线与直线相交于点,射线与直线相交于点,且.已知.
(1)用含有的代数式表示线段的长,______;
(2)①当点与点重合时,求线段的长;
②若点在线段上,求的范围;
(3)求的面积(用含的代数式表示).
四、解答题
20.(2024九上·六盘水期中)大明寺栖灵塔雄踞在古城扬州北郊蜀冈中峰之上,某数学兴趣小组决定利用所学知识测量栖灵塔的高度,如图,栖灵塔的高度为,在地面上取E,G两点,分别竖立两根高为的标杆和,两标杆间隔为47.5m,并且瑞光塔,标杆和在同一竖直平面内.从标杆后退到D处(即),从D处观察A点,A、F、D三点成一线;从标杆后退到C处(即),从C处观察A点,A、H、C三点也成一线.已知B、E、D、G、C在同一直线上,,,,请你根据以上测量数据,帮助兴趣小组求出栖灵塔的高度(结果精确到).
21.(2025·东台模拟)如图,阳阳要测量一座钟塔的高度,他在与钟塔底端处在同水平面上的地面放置一面镜子,并在镜子上做一个标记,当他站在离镜子处1.4m的处时,看到钟塔的顶端在镜子中的像与标记重合.已知,,在同直线上,阳阳的眼睛离地面的高度m,m,求钟塔的高度.
22.(2023九上·期末)如图所示,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由.
(2)连结AC,分别交BE,DF于点G,H,连结BD交AC于点.若,求BC的长.
23.(2024九下·长清模拟)如图,在平面直角坐标系中,抛物线经过,与y轴交于点,直线与x轴交于点C.
(1)求该抛物线的解析式;
(2)正比例函数的图象分别与线段,直线交于点D,E,当与相似时,求线段的长度;
(3)如图2,P是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以为一边的矩形,若存在,求出点F的坐标,若不存在,说明理由.
答案解析部分
1.【答案】C
【知识点】相似三角形的判定与性质
2.【答案】C
【知识点】相似三角形的判定与性质
3.【答案】C
【知识点】坐标与图形性质;两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】A
【知识点】相似三角形的判定与性质
5.【答案】B
【知识点】相似三角形的判定与性质
6.【答案】B
【知识点】相似三角形的判定与性质
7.【答案】D
【知识点】平行四边形的性质;相似三角形的判定与性质
8.【答案】A
【知识点】比例的性质
9.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
10.【答案】D
【知识点】余角、补角及其性质;正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】比例的性质
13.【答案】24
【知识点】比例的性质
14.【答案】
【知识点】相似三角形的应用
15.【答案】
【知识点】相似三角形的判定与性质
16.【答案】 或
【知识点】相似三角形的性质
17.【答案】13.44m
【知识点】相似三角形的应用
18.【答案】8米
【知识点】相似三角形的应用
19.【答案】(1)
(2)①或;②当时,点在线段上
(3)
【知识点】因式分解法解一元二次方程;勾股定理;矩形的判定与性质;相似三角形的判定与性质
20.【答案】栖灵塔的高度约为.
【知识点】相似三角形的应用
21.【答案】
【知识点】相似三角形的应用
22.【答案】(1)解:四边形BEDF的形状是平行四边形,
理由:∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC,
∴∠ABE=∠CDF,
∴∠EBF=∠EDF,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EDF=∠DFC=∠EBF,
∴BE∥DF,
∴AD∥BC,
∴四边形BEDF为平行四边形;
(2)解:∵,
∴设AG=2x,OG=3x,
∴AO=OC=5x,
∴GC=5x+5x-2x=8x,
∵AD∥BC,
∴△AEG∽△BCG,
∴即
解之:BC=16.
【知识点】平行四边形的判定与性质;相似三角形的应用
23.【答案】(1)
(2)
(3)存在,点的坐标为或
【知识点】矩形的性质;相似三角形的判定与性质;一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第22章 相似形综合测试题
一、单选题
1.(2020九上·江阴月考)如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是( )
A. B. C. D.
2.(2025九下·和平开学考)如图,点D,E分别在的边,上,且.,若,,则( )
A.9 B.8 C.6 D.4.5
3.(2025九下·潮南月考)如图,在平面直角坐标系中,为的边上一点,,过作交于点,、两点纵坐标分别为1、3,则点的纵坐标为( )
A.4 B.5 C.6 D.7
4.(2023·开远模拟)如图.在中,,若,则等于( )
A. B. C. D.
5.如图,在 中, ,则 的值是( )
A. B. C. D.
6.如图,小明把一个边长为10的正方形DEFG剪纸贴在△ABC纸片上,其中AB=AC=26,BC=20,正方形的顶点D,G分别在边AB、AC上,且AD=AG,点E、F在△ABC内部,则点E到BC的距离为( )
A.1 B.2 C. D.
7.(2021九上·嘉祥期中)如图, ABCD中,点E是AD的中点,EC交对角线BD于点F,则 ( )
A. B.2 C. D.
8.(2023九上·襄都期中)已知线段,如果,那么下列各式一定正确的是( )
A. B. C. D.
9.(2021九上·温州期末)如图, 是一组平行线,直线AC,DF分别与这组平行线依次相交于点A,B,C和点D,E,F.若 ,则 的值为( )
A. B. C. D.
10.(2024·杭州模拟)如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论正确的是( )
A.OA2=OE OP B.OQ2=OA OF
C.若BP=1,则OE=2 D.若BP=1,则
二、填空题
11.(2024九上·上海市月考)若,,则
12.(2023·成都模拟)若,且,则c= .
13.(2024九上·上海市月考)如果在比例尺为1:1000000的地图上,A、B两地的图上距离是2.4厘米,那么A、B两地的实际距离是 千米.
14.(2022九上·绍兴期中)如图,图1是装了液体的高脚杯,加入一些液体后如图2所示,则此时液面为 cm.
15.(2024九上·奉贤期中)在中,,为斜边上的高.若,则
16.在△ABC中,E是AB上一点,AE=2,BE=3,AC=4,在AC上取一点D,使△ADE与△ABC相似,则AD的长为 .
三、计算题
17.(2023九上·电白期中)小强在地面处放一面镜子,刚好能从镜子中看到教学楼的顶端此时米,米.已知眼睛距离地面的高度米,请计算出教学楼的高度.(根据光的反射定律,反射角等于入射角)
18.(2023九上·大洼月考)九(1)班同学到野外上数学活动课,为测量河的宽度(河的两岸平行),设计了如下方案:如图,同学们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量米,米,且点E到河岸的距离为6米.已知于点F,请你根据提供的数据,帮助他们计算河的宽度.
19.(2023九上·梁溪期中)在矩形中,为边上一点,且,点是线段上一动点,直线与直线相交于点,射线与直线相交于点,且.已知.
(1)用含有的代数式表示线段的长,______;
(2)①当点与点重合时,求线段的长;
②若点在线段上,求的范围;
(3)求的面积(用含的代数式表示).
四、解答题
20.(2024九上·六盘水期中)大明寺栖灵塔雄踞在古城扬州北郊蜀冈中峰之上,某数学兴趣小组决定利用所学知识测量栖灵塔的高度,如图,栖灵塔的高度为,在地面上取E,G两点,分别竖立两根高为的标杆和,两标杆间隔为47.5m,并且瑞光塔,标杆和在同一竖直平面内.从标杆后退到D处(即),从D处观察A点,A、F、D三点成一线;从标杆后退到C处(即),从C处观察A点,A、H、C三点也成一线.已知B、E、D、G、C在同一直线上,,,,请你根据以上测量数据,帮助兴趣小组求出栖灵塔的高度(结果精确到).
21.(2025·东台模拟)如图,阳阳要测量一座钟塔的高度,他在与钟塔底端处在同水平面上的地面放置一面镜子,并在镜子上做一个标记,当他站在离镜子处1.4m的处时,看到钟塔的顶端在镜子中的像与标记重合.已知,,在同直线上,阳阳的眼睛离地面的高度m,m,求钟塔的高度.
22.(2023九上·期末)如图所示,在 ABCD中,点E,F分别在边AD,BC上,且∠ABE=∠CDF.
(1)探究四边形BEDF的形状,并说明理由.
(2)连结AC,分别交BE,DF于点G,H,连结BD交AC于点.若,求BC的长.
23.(2024九下·长清模拟)如图,在平面直角坐标系中,抛物线经过,与y轴交于点,直线与x轴交于点C.
(1)求该抛物线的解析式;
(2)正比例函数的图象分别与线段,直线交于点D,E,当与相似时,求线段的长度;
(3)如图2,P是抛物线上位于第一象限的一个动点,在线段和直线上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以为一边的矩形,若存在,求出点F的坐标,若不存在,说明理由.
答案解析部分
1.【答案】C
【知识点】相似三角形的判定与性质
2.【答案】C
【知识点】相似三角形的判定与性质
3.【答案】C
【知识点】坐标与图形性质;两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】A
【知识点】相似三角形的判定与性质
5.【答案】B
【知识点】相似三角形的判定与性质
6.【答案】B
【知识点】相似三角形的判定与性质
7.【答案】D
【知识点】平行四边形的性质;相似三角形的判定与性质
8.【答案】A
【知识点】比例的性质
9.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
10.【答案】D
【知识点】余角、补角及其性质;正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】
【知识点】比例的性质
12.【答案】
【知识点】比例的性质
13.【答案】24
【知识点】比例的性质
14.【答案】
【知识点】相似三角形的应用
15.【答案】
【知识点】相似三角形的判定与性质
16.【答案】 或
【知识点】相似三角形的性质
17.【答案】13.44m
【知识点】相似三角形的应用
18.【答案】8米
【知识点】相似三角形的应用
19.【答案】(1)
(2)①或;②当时,点在线段上
(3)
【知识点】因式分解法解一元二次方程;勾股定理;矩形的判定与性质;相似三角形的判定与性质
20.【答案】栖灵塔的高度约为.
【知识点】相似三角形的应用
21.【答案】
【知识点】相似三角形的应用
22.【答案】(1)解:四边形BEDF的形状是平行四边形,
理由:∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC,
∴∠ABE=∠CDF,
∴∠EBF=∠EDF,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠EDF=∠DFC=∠EBF,
∴BE∥DF,
∴AD∥BC,
∴四边形BEDF为平行四边形;
(2)解:∵,
∴设AG=2x,OG=3x,
∴AO=OC=5x,
∴GC=5x+5x-2x=8x,
∵AD∥BC,
∴△AEG∽△BCG,
∴即
解之:BC=16.
【知识点】平行四边形的判定与性质;相似三角形的应用
23.【答案】(1)
(2)
(3)存在,点的坐标为或
【知识点】矩形的性质;相似三角形的判定与性质;一元二次方程的应用-几何问题;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
