23.2解直角三角形及其应用 同步练习(含答案)
文档属性
| 名称 | 23.2解直角三角形及其应用 同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 21:17:29 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
23.2解直角三角形及其应用
一、单选题
1.(2024九上·市南区期末)如图,小强从热气球上的A点测量一栋高楼顶部的仰角,测量这栋高楼底部的俯角,热气球与高楼的水平距离为米,则这栋高楼的高BC为( )米.
A.45 B.60 C.75 D.90
2.(2024九上·濮阳期末)河堤横断面迎水坡的坡度,若水平宽度为24米,则铅垂高度为( )
A.米 B. 米 C. 米 D. 米
3.(2023九上·安乡县期末)如图所示,某村准备在坡角为的山坡上栽树,要求相邻两棵树之间的水平距离为(m),那么这两棵树在坡面上的距离AB为( )
A.mcos(m) B.(m)
C.msin(m) D.(m)
4.(2023·鹿城模拟)如图是一款汽车千斤顶,其主要部件为四根连杆组成的菱形和螺旋杆,当,时,A,C两点的距离为( )
A. B. C. D.
5.(2024九上·大连月考)如图,太阳光线与地面成60°角,一棵倾斜的大树AB与地面成30°角,这时测得大树在地面的影长BC为10m,则大树的长为( )
A.m B.m C.m D.m
6.(2024八上·城关期末)如图,在中,,,于点D,于点E,.连接DE,将沿直线AE翻折至所在的平面内,得,连接DF.过点D作交BE于点G.则四边形DFEG的周长为( )
A.8 B. C. D.
7.如图,某水库堤坝横断面迎水坡AB的坡比是1:,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m C.150m D.50m
8.(2022九下·大埔期中)如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若,则BE的长是( )
A.5 B. C. D.
9.(2017九上·哈尔滨期中)如图,有一轮船在A处测得南偏东30°方向上有一小岛F,轮船沿正南方向航行至B处,测 得小岛F在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛F在正东方向上,则A,B之间距离是( )
A.10 海里 B.(10 -10)海里
C.10海里 D.(10 -10)海里
10.(2022八下·南浔期末)赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示).某次课后服务拓展学习上,小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1,大正方形ABCD的面积为S2,若DI=2,CI=1,S2=5S1,则GI的值是( )
A. B. C. D.
二、填空题
11.(2025·盐田模拟)如图,平地上一旗杆高为10米,两次观察地面上的影子,第一次太阳光线与地面成,第二次太阳光线与地面成,第二次观察到的影子比第一次长 米.(结果保留一位小数(参考数据:,,)
12.(2023九下·云梦模拟)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角,已知窗户的高度,窗台的高度,窗外水平遮阳篷的宽,则的长度为 (结果精确到).
13.(2024九下·黄石港模拟)如图所示,有一天桥高为5米,是通向天桥的斜坡,,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使,则的长度约为 (保留一位小数,参考数据:,)
14.(2025·黄浦模拟)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
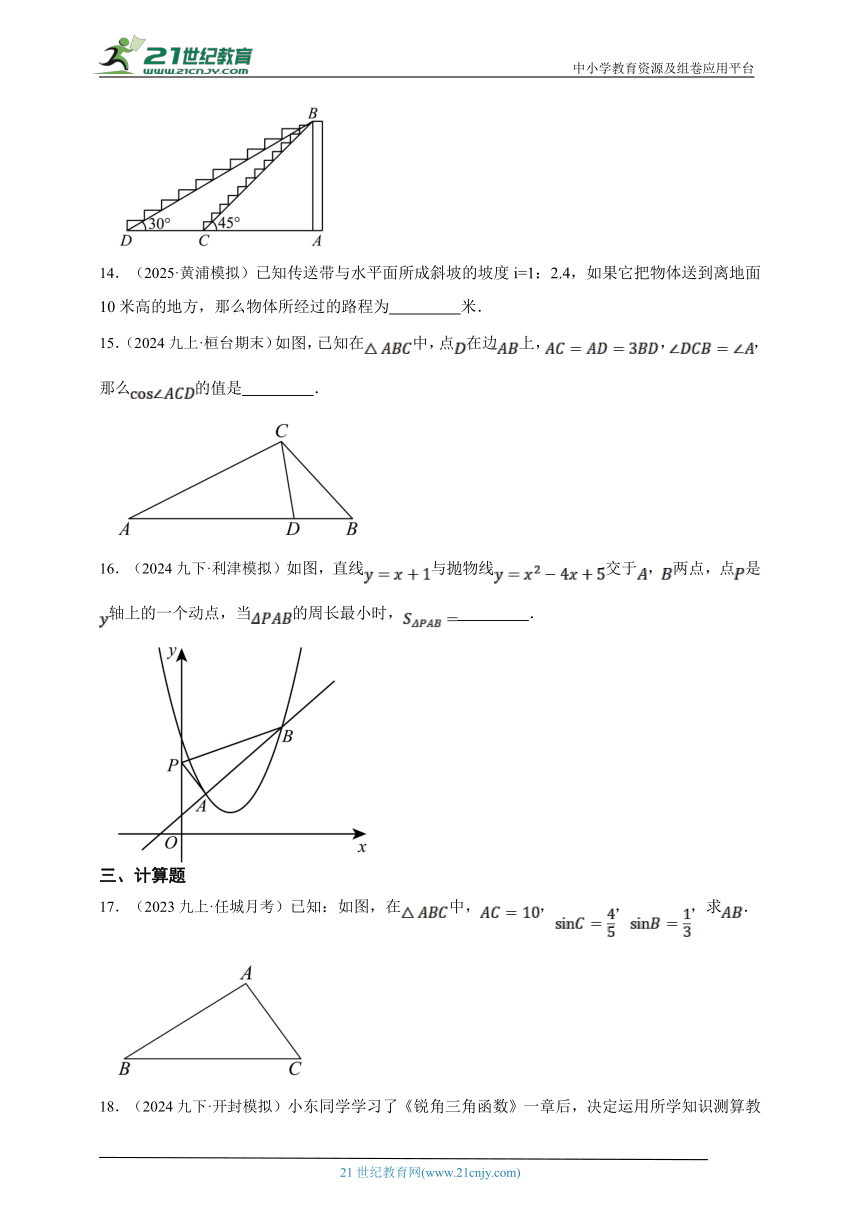
15.(2024九上·桓台期末)如图,已知在中,点在边上,,,那么的值是 .
16.(2024九下·利津模拟)如图,直线与抛物线交于,两点,点是轴上的一个动点,当的周长最小时, .
三、计算题
17.(2023九上·任城月考)已知:如图,在中,,,,求.
18.(2024九下·开封模拟)小东同学学习了《锐角三角函数》一章后,决定运用所学知识测算教室对面远处正在施工的塔吊(一种将重物吊到高处的建筑工具)的高度.小东现在所处的位置是四楼教室的点处,小东利用测角仪测得对面远处塔吊正在施工的六层(每层高)建筑物的顶部点的仰角为,测得被这幢六层建筑物遮住了一部分的塔吊的顶端点的仰角为.按照安全规定:此时塔吊的底部点距建筑物的底部点是.利用这些数据,小东经过详细的计算,得出塔吊的高度约为,但这个高度明显违反了此种塔吊使用的安全规定(塔吊的最高高度与建筑物的最高高度差必须保持在),亲爱的同学,你也来利用小东测得的数据,仔细算一算塔吊的高度,并判断该塔吊是否违规操作.(结果保留一位小数.参考数据:,,,,)
19.(2024九下·兴隆台模拟)根据背景素材,探索解决问题.
测算发射塔的高度
背景素材 某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度(如图1).他们通过自制的测倾仪(如图2)在,,三个位置观测,测倾仪上的示数如图3所示.
经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度.
问题解决
任务1 分析规划 选择两个观测位置:点_________和点_________
获取数据 写出所选位置观测角的正切值,并量出观测点之间的图上距离.
任务2 推理计算 计算发射塔的图上高度.
任务3 换算高度 楼房实际宽度为米,请通过测量换算发射塔的实际高度.
注:测量时,以答题纸上的图上距离为准,并精确到1.
四、解答题
20.(2025·礼县模拟)如图所示分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆,箱长,拉杆的长度都相等,即,点B,点F在线段上,点C在上,支杆,,,.求的长度.(结果保留一位小数,)
21.(2025·宁江模拟)小明和小强决定利用所的知识测量本校综合楼上安装的电信信号塔的高度,在操场上选取一点,测得信号塔顶点的仰角为,测得这栋楼的顶部的仰角为,又知,,三点在一条直线上,水平距离为,,,,三点在一条直线上且,,求信号塔本身的高(结果保留整数).
22.(2023·曾都模拟)随州文峰塔始建于唐宋年间,前身为“文笔塔”,民间亦称为“文丰塔”.某兴趣小组同学借助无人机航拍测量位于曾都区东城文峰塔广场的文峰塔高度.如图,无人机在距离地面米的A处,测得该塔底端点B的俯角为,然后向塔方向沿水平面飞行秒到达点C处,此时测得该塔顶端点D的俯角为.已知无人机的飞行速度为3米/秒.
(1)则无人机从A处到C处的水平飞行距离为______米;
(2)求文峰塔的高度.(参考数据:,,,,结果精确到米)
23.(2024九下·苏州模拟)图1,在平面直角坐标系中,的直角边在轴的正半轴上,且,斜边,点为线段上一动点.
(1)请直接写出点的坐标;
(2)若动点满足,求此时点的坐标;
(3)如图2,若点为线段的中点,连接,以为折痕,在平面内将折叠,点的对应点为,当时,求此时点的坐标;
(4)如图3,若为线段上一点,且,连接,将线段绕点顺时针方向旋转得线段,连接,当取最小值时,请直接写出的最小值和此时线段扫过的面积.
答案解析部分
1.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
4.【答案】C
【知识点】菱形的性质;解直角三角形
5.【答案】B
【知识点】解直角三角形
6.【答案】D
【知识点】勾股定理;解直角三角形
7.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】D
【知识点】翻折变换(折叠问题);解直角三角形
9.【答案】D
【知识点】解直角三角形;解直角三角形的实际应用﹣方向角问题
10.【答案】A
【知识点】勾股定理;勾股定理的应用;解直角三角形
11.【答案】9.6
【知识点】解直角三角形;等腰直角三角形
12.【答案】4.4m
【知识点】解直角三角形的其他实际应用
13.【答案】3.7米
【知识点】解直角三角形的其他实际应用
14.【答案】26
【知识点】解直角三角形的实际应用﹣坡度坡角问题
15.【答案】
【知识点】相似三角形的判定与性质;解直角三角形
16.【答案】.
【知识点】二次函数的最值;解直角三角形
17.【答案】
【知识点】解直角三角形
18.【答案】塔吊的高度为:,塔吊没有违规操作.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】规划一:[任务 1]选择点和点;,,,测得图上;[任务 2];[任务 3]发射塔的实际高度为米;规划二:[任务 1]选择点和点.[任务 2];[任务 3]发射塔的实际高度为米;
【知识点】解直角三角形的其他实际应用
20.【答案】
【知识点】解直角三角形的其他实际应用
21.【答案】信号塔本身的高为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】(1)
(2)米
【知识点】解直角三角形的实际应用﹣仰角俯角问题;有理数乘法的实际应用
23.【答案】(1)
(2)
(3)
(4)的最小值为4,
【知识点】勾股定理;相似三角形的判定与性质;解直角三角形;三角形全等的判定-SAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
23.2解直角三角形及其应用
一、单选题
1.(2024九上·市南区期末)如图,小强从热气球上的A点测量一栋高楼顶部的仰角,测量这栋高楼底部的俯角,热气球与高楼的水平距离为米,则这栋高楼的高BC为( )米.
A.45 B.60 C.75 D.90
2.(2024九上·濮阳期末)河堤横断面迎水坡的坡度,若水平宽度为24米,则铅垂高度为( )
A.米 B. 米 C. 米 D. 米
3.(2023九上·安乡县期末)如图所示,某村准备在坡角为的山坡上栽树,要求相邻两棵树之间的水平距离为(m),那么这两棵树在坡面上的距离AB为( )
A.mcos(m) B.(m)
C.msin(m) D.(m)
4.(2023·鹿城模拟)如图是一款汽车千斤顶,其主要部件为四根连杆组成的菱形和螺旋杆,当,时,A,C两点的距离为( )
A. B. C. D.
5.(2024九上·大连月考)如图,太阳光线与地面成60°角,一棵倾斜的大树AB与地面成30°角,这时测得大树在地面的影长BC为10m,则大树的长为( )
A.m B.m C.m D.m
6.(2024八上·城关期末)如图,在中,,,于点D,于点E,.连接DE,将沿直线AE翻折至所在的平面内,得,连接DF.过点D作交BE于点G.则四边形DFEG的周长为( )
A.8 B. C. D.
7.如图,某水库堤坝横断面迎水坡AB的坡比是1:,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.100m C.150m D.50m
8.(2022九下·大埔期中)如图,直线MN是矩形ABCD的一条对称轴,点E在AD边E上,将沿BE折叠,使点A的对应点F落在直线MN上,若,则BE的长是( )
A.5 B. C. D.
9.(2017九上·哈尔滨期中)如图,有一轮船在A处测得南偏东30°方向上有一小岛F,轮船沿正南方向航行至B处,测 得小岛F在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛F在正东方向上,则A,B之间距离是( )
A.10 海里 B.(10 -10)海里
C.10海里 D.(10 -10)海里
10.(2022八下·南浔期末)赵爽弦图由四个全等的直角三角形所组成,形成一个大正方形,中间是一个小正方形(如图所示).某次课后服务拓展学习上,小浔绘制了一幅赵爽弦图,她将EG延长交CD于点I.记小正方形EFGH的面积为S1,大正方形ABCD的面积为S2,若DI=2,CI=1,S2=5S1,则GI的值是( )
A. B. C. D.
二、填空题
11.(2025·盐田模拟)如图,平地上一旗杆高为10米,两次观察地面上的影子,第一次太阳光线与地面成,第二次太阳光线与地面成,第二次观察到的影子比第一次长 米.(结果保留一位小数(参考数据:,,)
12.(2023九下·云梦模拟)如图,某一时刻太阳光从窗户射入房间内,与地面的夹角,已知窗户的高度,窗台的高度,窗外水平遮阳篷的宽,则的长度为 (结果精确到).
13.(2024九下·黄石港模拟)如图所示,有一天桥高为5米,是通向天桥的斜坡,,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使,则的长度约为 (保留一位小数,参考数据:,)
14.(2025·黄浦模拟)已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 米.
15.(2024九上·桓台期末)如图,已知在中,点在边上,,,那么的值是 .
16.(2024九下·利津模拟)如图,直线与抛物线交于,两点,点是轴上的一个动点,当的周长最小时, .
三、计算题
17.(2023九上·任城月考)已知:如图,在中,,,,求.
18.(2024九下·开封模拟)小东同学学习了《锐角三角函数》一章后,决定运用所学知识测算教室对面远处正在施工的塔吊(一种将重物吊到高处的建筑工具)的高度.小东现在所处的位置是四楼教室的点处,小东利用测角仪测得对面远处塔吊正在施工的六层(每层高)建筑物的顶部点的仰角为,测得被这幢六层建筑物遮住了一部分的塔吊的顶端点的仰角为.按照安全规定:此时塔吊的底部点距建筑物的底部点是.利用这些数据,小东经过详细的计算,得出塔吊的高度约为,但这个高度明显违反了此种塔吊使用的安全规定(塔吊的最高高度与建筑物的最高高度差必须保持在),亲爱的同学,你也来利用小东测得的数据,仔细算一算塔吊的高度,并判断该塔吊是否违规操作.(结果保留一位小数.参考数据:,,,,)
19.(2024九下·兴隆台模拟)根据背景素材,探索解决问题.
测算发射塔的高度
背景素材 某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度(如图1).他们通过自制的测倾仪(如图2)在,,三个位置观测,测倾仪上的示数如图3所示.
经讨论,只需选择其中两个合适的位置,通过测量、换算就能计算发射塔的高度.
问题解决
任务1 分析规划 选择两个观测位置:点_________和点_________
获取数据 写出所选位置观测角的正切值,并量出观测点之间的图上距离.
任务2 推理计算 计算发射塔的图上高度.
任务3 换算高度 楼房实际宽度为米,请通过测量换算发射塔的实际高度.
注:测量时,以答题纸上的图上距离为准,并精确到1.
四、解答题
20.(2025·礼县模拟)如图所示分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆,箱长,拉杆的长度都相等,即,点B,点F在线段上,点C在上,支杆,,,.求的长度.(结果保留一位小数,)
21.(2025·宁江模拟)小明和小强决定利用所的知识测量本校综合楼上安装的电信信号塔的高度,在操场上选取一点,测得信号塔顶点的仰角为,测得这栋楼的顶部的仰角为,又知,,三点在一条直线上,水平距离为,,,,三点在一条直线上且,,求信号塔本身的高(结果保留整数).
22.(2023·曾都模拟)随州文峰塔始建于唐宋年间,前身为“文笔塔”,民间亦称为“文丰塔”.某兴趣小组同学借助无人机航拍测量位于曾都区东城文峰塔广场的文峰塔高度.如图,无人机在距离地面米的A处,测得该塔底端点B的俯角为,然后向塔方向沿水平面飞行秒到达点C处,此时测得该塔顶端点D的俯角为.已知无人机的飞行速度为3米/秒.
(1)则无人机从A处到C处的水平飞行距离为______米;
(2)求文峰塔的高度.(参考数据:,,,,结果精确到米)
23.(2024九下·苏州模拟)图1,在平面直角坐标系中,的直角边在轴的正半轴上,且,斜边,点为线段上一动点.
(1)请直接写出点的坐标;
(2)若动点满足,求此时点的坐标;
(3)如图2,若点为线段的中点,连接,以为折痕,在平面内将折叠,点的对应点为,当时,求此时点的坐标;
(4)如图3,若为线段上一点,且,连接,将线段绕点顺时针方向旋转得线段,连接,当取最小值时,请直接写出的最小值和此时线段扫过的面积.
答案解析部分
1.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
2.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
3.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
4.【答案】C
【知识点】菱形的性质;解直角三角形
5.【答案】B
【知识点】解直角三角形
6.【答案】D
【知识点】勾股定理;解直角三角形
7.【答案】A
【知识点】解直角三角形的实际应用﹣坡度坡角问题
8.【答案】D
【知识点】翻折变换(折叠问题);解直角三角形
9.【答案】D
【知识点】解直角三角形;解直角三角形的实际应用﹣方向角问题
10.【答案】A
【知识点】勾股定理;勾股定理的应用;解直角三角形
11.【答案】9.6
【知识点】解直角三角形;等腰直角三角形
12.【答案】4.4m
【知识点】解直角三角形的其他实际应用
13.【答案】3.7米
【知识点】解直角三角形的其他实际应用
14.【答案】26
【知识点】解直角三角形的实际应用﹣坡度坡角问题
15.【答案】
【知识点】相似三角形的判定与性质;解直角三角形
16.【答案】.
【知识点】二次函数的最值;解直角三角形
17.【答案】
【知识点】解直角三角形
18.【答案】塔吊的高度为:,塔吊没有违规操作.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
19.【答案】规划一:[任务 1]选择点和点;,,,测得图上;[任务 2];[任务 3]发射塔的实际高度为米;规划二:[任务 1]选择点和点.[任务 2];[任务 3]发射塔的实际高度为米;
【知识点】解直角三角形的其他实际应用
20.【答案】
【知识点】解直角三角形的其他实际应用
21.【答案】信号塔本身的高为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】(1)
(2)米
【知识点】解直角三角形的实际应用﹣仰角俯角问题;有理数乘法的实际应用
23.【答案】(1)
(2)
(3)
(4)的最小值为4,
【知识点】勾股定理;相似三角形的判定与性质;解直角三角形;三角形全等的判定-SAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
