1.4.1角平分线的性质(共14张PPT)湘教版数学八年级下册
文档属性
| 名称 | 1.4.1角平分线的性质(共14张PPT)湘教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
1.4.1角平分线的性质
湘教版·八年级数学下册
复习导入
一
思考:
(1)角平分线的定义是怎样的
探究新知一
一
一:折一折
把∠AOB的纸片对折OA和OB边重合,然后展开,这条折痕所在的射线为这个角的________
二:量一量
重合后,再将纸片折叠,使O点在落在OA边上,再展开得到两边折痕,量一量这两条边折痕以及分别与∠AOB两边OA,OB形成的夹角度数
平分线
已知:OC平分∠AOB,点P在 OC上,PD⊥OA于点D,PE⊥OB于点E
求证:PD=PE
猜想:角平分线上的点到角两边的距离相等
证明:∵OC平分∠AOB , ∴ ∠1=∠2
∵PD⊥OA,PE⊥OB , ∴∠PDO=∠PEO= 90°.
在△PDO和△PEO中
∠PDO=∠PEO
∠1=∠2
OP=OP(公共边)
∴△PDO≌△PEO(AAS)
∴PD= PE.
A
D
O
P
C
E
B
图1-26
1
2
总结归纳
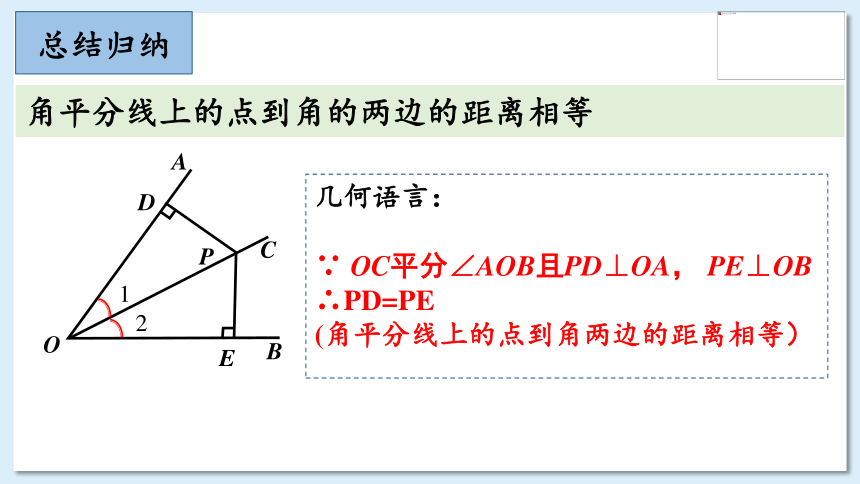
角平分线上的点到角的两边的距离相等
几何语言:
∵ OC平分∠AOB且PD⊥OA, PE⊥OB
∴PD=PE
(角平分线上的点到角两边的距离相等)
A
D
O
P
C
E
B
1
2
A
C
O
P
D
B
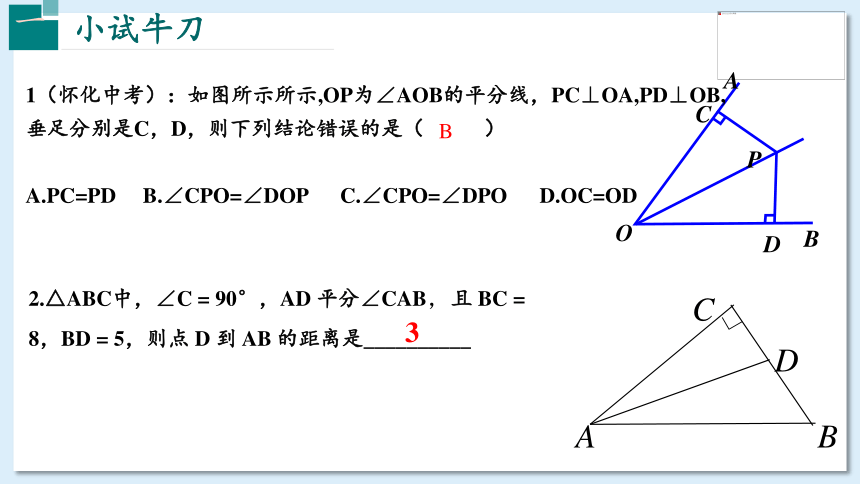
1(怀化中考):如图所示所示,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
垂足分别是C,D,则下列结论错误的是( )
A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
B
小试牛刀
一
2.△ABC中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是__________
A
B
C
D
∟
3
探究新知二
一
角平分线上的点到角的两边的距离相等
角平分线的性质定理:
那么:
如果:
一个点在角的平分线上
这个点到角的两边的距离相等
角的内部
已知:PD⊥OA,PE⊥OB,垂足分别为点D,E,PD=PE
求证:点P在∠AOB的平分线上
证明:如图1-27,过点O,P作射线OC.
∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO= 90°.
在Rt△PDO和Rt△PEO中,
OP=OP
PD=PE
∴Rt△PDO≌Rt△PEO (HL)
.∴∠1=∠2
∴OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.
O
A
B
D
E
P
C
1
2
角的内部到角的两边距离相等的点在角的平分线上
几何语言:
∵ PD⊥OA,PE⊥OB, PD=PE
∴ 点P在∠AOB的平分线上
(角的内部到角的两边距离相等的点在角的平分线上)
总结归纳
P
A
D
O
C
E
B
例题解析
一
如图 ∠BAD=∠BCD=90°,∠1=∠2.
(1)求证: 点B在∠ADC的平分线上;
(2)求证: BD平分∠ABC.
3
4
【教材P23】
证明:(1)在△ABC中,
∵∠l=∠2,∴BA = BC.
又BA⊥AD, BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD,
∴Rt△BAD≌Rt△BCD(HL)
∴∠3=∠4
∴BD平分∠ABC.
3
4
如图,在△ABC中,AD平分∠BAC, DE⊥AB于点E,
DF⊥AC于点F, BD=CD. 求证: AB=AC.
证明:∵AD为∠BAC的平分线,
DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
在Rt△BDE和Rt△CDF中,∵BD=CD,
∴ Rt△BED≌Rt△CFD(HL)
∴∠B=∠C. ∴AB=AC (等角对等边).
变式练习
一
如图,一个工厂在A区,它到公路、铁路的距离相等,并且离
公路和铁路的交叉处O点为500m,在图上标出它的位置
(比例尺为1∶20000).
解:
500÷20000=0.025m,
0.025m=2.5cm
图上距离为2.5cm.
E
F
C
P
点P即为所求.
问题解决
一
【教材P26】
1.角平分线的性质定理:
角平分线上的点到角的两边的距离相等
2.角平分线的性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上
课堂小结
一
1.4.1角平分线的性质
湘教版·八年级数学下册
复习导入
一
思考:
(1)角平分线的定义是怎样的
探究新知一
一
一:折一折
把∠AOB的纸片对折OA和OB边重合,然后展开,这条折痕所在的射线为这个角的________
二:量一量
重合后,再将纸片折叠,使O点在落在OA边上,再展开得到两边折痕,量一量这两条边折痕以及分别与∠AOB两边OA,OB形成的夹角度数
平分线
已知:OC平分∠AOB,点P在 OC上,PD⊥OA于点D,PE⊥OB于点E
求证:PD=PE
猜想:角平分线上的点到角两边的距离相等
证明:∵OC平分∠AOB , ∴ ∠1=∠2
∵PD⊥OA,PE⊥OB , ∴∠PDO=∠PEO= 90°.
在△PDO和△PEO中
∠PDO=∠PEO
∠1=∠2
OP=OP(公共边)
∴△PDO≌△PEO(AAS)
∴PD= PE.
A
D
O
P
C
E
B
图1-26
1
2
总结归纳
角平分线上的点到角的两边的距离相等
几何语言:
∵ OC平分∠AOB且PD⊥OA, PE⊥OB
∴PD=PE
(角平分线上的点到角两边的距离相等)
A
D
O
P
C
E
B
1
2
A
C
O
P
D
B
1(怀化中考):如图所示所示,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,
垂足分别是C,D,则下列结论错误的是( )
A.PC=PD B.∠CPO=∠DOP C.∠CPO=∠DPO D.OC=OD
B
小试牛刀
一
2.△ABC中,∠C = 90°,AD 平分∠CAB,且 BC = 8,BD = 5,则点 D 到 AB 的距离是__________
A
B
C
D
∟
3
探究新知二
一
角平分线上的点到角的两边的距离相等
角平分线的性质定理:
那么:
如果:
一个点在角的平分线上
这个点到角的两边的距离相等
角的内部
已知:PD⊥OA,PE⊥OB,垂足分别为点D,E,PD=PE
求证:点P在∠AOB的平分线上
证明:如图1-27,过点O,P作射线OC.
∵PD⊥OA,PE⊥OB,∴∠PDO=∠PEO= 90°.
在Rt△PDO和Rt△PEO中,
OP=OP
PD=PE
∴Rt△PDO≌Rt△PEO (HL)
.∴∠1=∠2
∴OC是∠AOB的平分线,即点P在∠AOB的平分线OC上.
O
A
B
D
E
P
C
1
2
角的内部到角的两边距离相等的点在角的平分线上
几何语言:
∵ PD⊥OA,PE⊥OB, PD=PE
∴ 点P在∠AOB的平分线上
(角的内部到角的两边距离相等的点在角的平分线上)
总结归纳
P
A
D
O
C
E
B
例题解析
一
如图 ∠BAD=∠BCD=90°,∠1=∠2.
(1)求证: 点B在∠ADC的平分线上;
(2)求证: BD平分∠ABC.
3
4
【教材P23】
证明:(1)在△ABC中,
∵∠l=∠2,∴BA = BC.
又BA⊥AD, BC⊥CD,
∴点B在∠ADC的平分线上.
(2)在Rt△BAD和Rt△BCD中,
∵BA=BC,BD=BD,
∴Rt△BAD≌Rt△BCD(HL)
∴∠3=∠4
∴BD平分∠ABC.
3
4
如图,在△ABC中,AD平分∠BAC, DE⊥AB于点E,
DF⊥AC于点F, BD=CD. 求证: AB=AC.
证明:∵AD为∠BAC的平分线,
DE⊥AB于E,DF⊥AC于F,
∴DE=DF.
在Rt△BDE和Rt△CDF中,∵BD=CD,
∴ Rt△BED≌Rt△CFD(HL)
∴∠B=∠C. ∴AB=AC (等角对等边).
变式练习
一
如图,一个工厂在A区,它到公路、铁路的距离相等,并且离
公路和铁路的交叉处O点为500m,在图上标出它的位置
(比例尺为1∶20000).
解:
500÷20000=0.025m,
0.025m=2.5cm
图上距离为2.5cm.
E
F
C
P
点P即为所求.
问题解决
一
【教材P26】
1.角平分线的性质定理:
角平分线上的点到角的两边的距离相等
2.角平分线的性质定理的逆定理:
角的内部到角的两边距离相等的点在角的平分线上
课堂小结
一
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
